Etude et modelisation des supercondensateurs

3.4.4. Modèle thermique du supercondensateur

La température due à l'autoéchauffement est une grandeur importante dans un supercondensateur, elle est à l'origine du vieillissement. L'objectif de cette partie est de présenter une étude simple de l'origine de l'autoéchauffement et une modélisation simplifiée du comportement thermique.

3.4.4.1. Source de chaleur

Nous pouvons constater dans un supercondensateur que la production de chaleur est la superposition de générations irréversible et réversible de chaleur [96, 123, 124].

3.4.4.1.1. Génération de chaleur irréversible

La génération irréversible de chaleur, due à l'effet Joule, est la puissance dissipée dans les résistances ohmiques. La puissance dissipée peut être estimée pour une fréquence donnée à partir du modèle à simple pore (cf. eq. 3-42) en considérant _Ieff courant efficace dans le composant.

P th = ESR . Ieff ²3-42

3.4.4.1.2. Génération de chaleur réversible

Trois causes pour une génération de chaleur réversible sont possibles : des réactions chimiques d'oxydoréduction, l'effet Peltier et la variation de l'entropie [123-126]. L'autoéchauffement lié aux réactions d'oxydoréduction est dépendant de la tension. Les ions dans l'électrolyte d'une double couche sont organisés par le champ électrique pendant la charge

et se répandent à nouveau pendant la décharge : l'entropie peut être interprétée comme une mesure d'agitation. L'effet de Peltier pour les contacts entre l'aluminium et le charbon se traduit par une variation de température de quelques uK, qui est proportionnelle au courant appliqué. Ce dernier dans un supercondensateur à base de charbon et électrolyte organique peut être négligé [123, 124].

3.4.4.2. Impédance thermique

Fondamentalement, la propagation de la chaleur issue d'un composant peut s'effectuer de trois manières : par conduction, par convection, et par radiation [20, 123, 124].

Le circuit équivalent de l'impédance de diffusion de la chaleur se base sur la théorie des lignes de transmission [20, 127]. Il décrit correctement la distribution de la température interne du système et permet une corrélation claire entre éléments équivalents et éléments physiques. 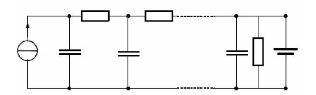Il existe d'autres réseaux capables de décrire correctement le comportement thermique et plus facile à identifier mais la structure interne du réseau n'a pas de correspondance physique évidente [128, 127]. La figure 3-79 montre le circuit équivalent considéré.

Pth

è1 è2

Rth1 Rth2 è_n

Cth 1 Cth2 Cthn

Rthn

è 0

Fig. 3-79 : Modèle thermique du supercondensateur à base de ligne de transmission

Il est clair, que l'identification de tous ces éléments par des mesures de température diverses à la surface et à l'intérieur du composant n'est pas envisageable. Le modèle équivalent devrait alors être simplifié pour obtenir un modèle identifiable. Le modèle simplifié proposé est basé sur l'hypothèse simplificatrice suivante : la température aux bornes et au coeur du supercondensateur est identique en régime permanent [129].

La température des bornes peut représenter la température à l'intérieur du supercondensateur car elles sont reliées directement aux collecteurs de courant en aluminium de conductivité thermique élevée. Des mesures ont été effectuées par l'Institut Paul Scherrer pour Maxwell en plaçant un thermocouple au centre du supercondensateur et un autre sur la borne positive. Les ré sultats ont montré que ces deux températures étaient pratiquement identiques [20].

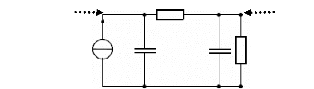
La figure 3-80 représente un modèle thermique simplifié composé de deux constantes de temps. Ce modèle considère les températures du boîtier et des bornes [130].

Le flux thermique _Pth représente la puissance provenant de l'effet Joule en négligeant la source de chaleur réversible. La source de chaleur réversible peut être négligée pour une simple modélisation d'un supercondensateur, car sa constante de temps thermique est très supérieure aux périodes de charge/décharge [35, 131]. Ce flux de chaleur s'écoule dans les résistances thermiques _Rth1 ^et _Rth2 (en °C/W) et les capacités _Cth1 ^et _Cth2 (en J/°C) pour provoquer la chute de la température Äè (en °C) sur le composant. La température ambiante è_o est assimilée, dans le circuit équivalent, à une source de tension constante.

Cth1 Cth2

Pth

Rth2

Coeur (bornes) è_c Rth1 èb Boîtier

è0

Fig. 3-80 : Modèle thermique simplifié du supercondensateur

L'impédance thermique peut être écrite par la relation suivante à partir du circuit équivalent :

Z = R C + R

th ( ( th 2 // th 2 ) th 1 ) // th 1

C3-43

Avec le formalisme en p (variable de Laplace) _Zth peut exprimée ainsi :

1 + R th 1

R th 1

ô . p 1 + ô .

th 2 th 2

p

ô 2th p )

Z = ( R R

+

th th 1 th 2

3-44

)

1+

R R

+ R R

+

th 1 th 2 th 1 th 2

? ( R R

ô + ô +

1 p + ô ô

2 p R C p

2 1 1 2 p

th th th th th th

+ )

p

2 th 1 th 2 (1 + ô )(1

1 p +

th

avec

ô th 1

)C th 1 3-45

= ( R R

+

th 1 th 2

ô =

th 2 ( ₂ ) 2

R C

th th

L'expression 3-44 utilise l'hypothèse simplificatrice que la constante de temps thermique ôth2 est très grande par rapport à _ôth1 [132].

La montée en température entre le coeur (bornes) du composant et l'ambiance est donc :

Äè_c = P thZ th 3-46

L'évolution temporelle de la température du coeur du composant est alors gouvernée par cette expression :

? ? t ? ? ? t ? ? ?

?-

Ä ( )

t P R

= 1 exp ?-

è ?

th ? ? - ? ? ?? + R ? 1 exp

- ? ? ?? 3-47

1

c th th 2

? ? ? ? ô 1 ? ? ? ? ô2 ? ? ? ?

L'évolution de la température sur le boîtier, quant à elle, est donnée comme suit :

? t ? t

1

- ??- + ?-

ô

Ä è t P _th R th

= ? ? exp

b ( ) 2 1 exp ?

? ? ô2 ? ô 2 ? ô 1

? ?

?? 3-48

? ?

3.4.4.3. Réponse thermique du supercondensateur

3.4.4.3.1. Outil de mesure

La mesure de la température sur la surface du supercondensateur a été effectuée à l'aide de thermocouples de type K liés au système d'acquisition multivoies de National Instrument (NI 9211). Les caractéristiques techniques du système d'acquisition sont données dans l'annexe D. Ce système est programmé sous le logiciel LabView. L'acquisition de données est effectuée en temps réel.

Nous présentons sur la figure 3-81 la position des cinq thermocouples employés pour la mesure. Sur un composant BCAP010, trois sont collés sur l'extérieur du boîtier et deux sur les bornes. Un sixième thermocouple pour la température ambiante de la salle de manipulation est loin du composant (sachant que la convection est naturelle et que la salle climatisée est à 25 °C).

Fig. 3-81 : Position des thermocouples sur le supercondensateur

3.4.4.3.2. Essai expérimental

Le dispositi

f expérimental employé pour effectuer la charge/décharge est un banc Arbin (cf. annexe E) permettant d'effectuer des charges décharges à courant constant, puissance constante, ...

Le comportement thermique pendant la charge (exothermique) est différent de celui pendant la décharge (exothermique et endothermique). Afin de mesurer la température aussi précisément que possible, des pauses ont été ajoutées après chaque étape.

Nous avons chargé et déchargé le supercondensateur par à courant constant de 100 A avec un rapport cyclique de 0,83 à partir d'une tension initiale de UN/2 un

pendant

peu plus d'une heure. Ensuite, nous l'avons laissé se refroidir. Le profil du courant est montré sur la figure 3- 82-a et l'évolution de la tension aux bornes du supercondensateur pendant l'essai expérimental sur la figure 3-82-b.

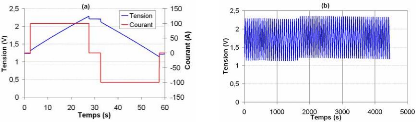
Fig. 3-82 : Evolution de la tension aux bornes du supercondensateur durant l'essai thermique

La réponse thermique du supercondensateur présentée sur la figure 3-83 montre les différente s températures dans le supercondensateur en fonction de tem

ps. La température aux

bornes du supercondensateur est supérieure aux autres. Les te

mpératures mesurées à

différentes positions du boîtier sont pratiquement les mêmes. Les résultats de la fi

gure

montrent que le régime permanent est atteint au bout d'une heure environ.

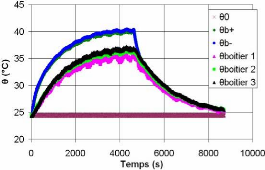
Fig. 3-83 : Evolution des températures du supercondensateur pour le profil présenté

3.4.4.3.3. Simulation et validation du modèle thermique

Les résultats expérimentaux montrés sur la figure 3-83 nous permettent de déterminer les éléments du modèle établi sur la figure 3-80. En régime permanant les résistances thermiques peuvent être e stimées par la puissance dissipée et l'augmentation des températures (cf. eq. 3- 49 ).

Äè Ä è

b c

R 2 = , R R

+ = 3-49

th th 1 th 2

P P

th th

Les capacités thermiques peuvent être calculées à partir des constantes de temps déterminées par un logiciel de "fitting" avec une erreur de moins de 1% (cf. eq. 3-50).

1

ô

th

1

Cth

3-50

R R

+

th 1 th 2

ô th 2

Rth 2

Cth

2

Ces éléments sont présentés dans le tableau 3-15 ci-dessous.

Elément	Rth1^(°C/W)	Rth2^(°C/W)	Cth1^(J/°C)		Cth2 (J/°C)	Valeur
0,7	2,88	172	433

Tab. 3-15 : Eléments du modèle thermique du supercondensateur

Par ailleurs, nous avons couplé le modèle thermique avec le modèle électrique avec des pores non-homogènes. Les valeurs de la résistance électrique ESR(è) sont ajustées suivant la température du composant par la loi établie auparavant. Le modèle à été implanté dans le logiciel Simplorer. La comparaison entre la simulation du modèle et les résultats expérimentaux est montrée sur la figure 3-84. Le modèle thermique établi représente avec une bonne précision pour un profil de courant donné l'évolution de la température du supercondensateur aux bornes (coeur) et à l'extérieur du boîtier.

Par contre il est bien évident que ce modèle n'est pas capable de modéliser les régimes transitoires thermiques rapides (de l'ordre de quelques secondes à quelques minutes) du supercondensateur. Pour prédire le comportement thermique en régime transitoire une modélisation analytique est nécessaire comme celle basé sur la méthode des différences finies [133].

Fig. 3-84 : Réponse thermique du modèle du supercondensateur schématisé sur la figure 3-84

Un autre essai thermique sévère avec un courant de charge/décharge de 400 A a été effectué dans l'objectif de montrer les points les plus chauds sur la surface du supercondensateur. La figure 3-85 montre que la température aux bornes dépasse la température maximale limite du supercondensateur.

Fig. 3-85 : Evolution des températures aux bornes et sur le boîtier du composant

A l'aide d'une caméra infrarouge, nous avons relevé des images thermiques du supercondensateur. La figure 3-86 correspond à l'image thermique obtenue quelques instants avant l'annulation du courant de charge/décharge (instant indiqué de couleur différente sur la figure 3-85). Nous constatons sur la figure que les points les plus chauds, comme prévus sont les bornes et qu'il y a une légère augmentation de la température du centre du boîtier vers l'extérieur du boîtier (prés des bornes).

Fig. 3-86 : Thermographie du supercondensateur