5.2.2. Origine de la dispersion des paramètres
des supercondensateurs
d'un module
La tension totale Umod sur le
système de supercondensateurs est la somme des tensions de chaque
cellule Usci. Cette tension
(Umod) et le courant parcourant les cellules sont
normalement co trôlés et ne doivent pas dépasser les
n limites prédéterminées.
Généralement, la tension de
l'
chaque cellule n'est pas contrôlée. Or, la
stabilité du fonctionnement de ce système dépend de
état de cellules qui le composent, c'est-à-dire de la
distribution de la tension sur les cellules. Dans le cas où toutes les
cellules ont des paramètres égaux, elles ne subiront pas de
contrainte locale, car l a distribution de la tension est homogène. Par
contre dans le cas réel où les paramètres des cellules de
supercondensateurs sont dispersés, une surtension sur une cellule peut
apparaître. Cette dispersion est due à la température et au
vieillissement non homogène, et à la dispersion de
fabrication.
5.2.2.1. Dispersion de fabrication des
supercondensateurs
Bien que des améliorations continues des techniques de
production des supercondensateurs chez les fabricants soient mises en oeuvre,
comme une grande automatisation des équipements de production, une
dispersion importante peut se manifester sur les différents
paramètres des composants produits dans une série.
La dispersion des paramètres des supercondensateurs
produits par le même fabricant comme MAXWELL peut atteindre #177; 20%
pour la capacité, #177; 25% pour la résistance série [28]
et #177; 30% pour la résistance de fuite [129, 149].
Nous nous proposons d'analyser les divers cas de dispersion des
paramètres des supercondensateurs et de voir leurs effets sur le nombre
des cellules à mettre en série (n).
5.2.2.1.1. Cas de la dispersion de la résistance
de fuite
Dans les applications avec un rapport cyclique bas, la
rapidité de l'autodécharge peut conduire à une
distribution non uniforme de la tension des cellules. A la fin de charge,
toutes les cellules de supercondensateur d'un module ont la même tension
à leurs bornes si la résistance ESR et la
capacité C de chaque cellule sont similaires. Malgré
cela, des autodécharges différentes peuvent avec le temps
déséquilibrer les tensions aux bornes des cellules. En effet, la
tens ion aux bornes des cellules ayant une autodécharge
élevée décroît plus rapidement que la tension des
autres cellules. Plus la valeur de la résistance de fuite Rfi
est élevée plus la tension de la cellule sera
élevée.
En supposant le nombre de cellule n très
élevé, la résistance de fuite totale du module est

donnée par n R f (avec R f moyenne des
résistance Rfi) . La tension Uscmax de la cellule
ayant la
résistance de fuite la plus élevée
Rfmax peut être donnée en fonction de la
tension du module Umod et du nombre de cellules n par la
relation suivante [149] :
U sc
|
= ma x Umod
|
R fmax
. 5-3
n.R f
|
|
Nous exprimons la résistance de fuite
Rfmax par l'équation suivante [149] :
R fmax= Rf. (1
+Kf)
5-4
Kf étant le facteur relatif de la dispersion
de la résistance de fuite par rapport à la moyenne des
résistances de fuite du module. Ce facteur peut être donc
donné par la formule suivante [149] :

R f max-Rf
K f = 5-5
Rf
Pour une tension du module et une tension de cellule i
données le nombre requis de cellules peut être calculé par
la relation suivante :
n = Umod . (1 )
Usci
+ Kf 5-6
Pour un facteur de dispersion Kf variant entre 0%
à 60% [149] et pour un composant d'une tension nominale de 2,5 V, nous
présentons sur la figure 5-3 le nombre de cellules en série en
fonction de la tension du module. Nous constatons qu'à tension
élevée et pour une dispersion importante de la résistance
de fuite, il est nécessaire d'augmenter le nombre de cellules en
série par rapport au cas idéal (sans dispersion). Afin de
réduire le nombre de cellules, la dispersion de la résistance de
fuite doit donc être la plus faible possible.
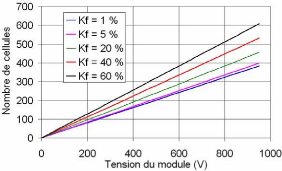
Fig. 5-3 : Nombre de cellules en fonction de la tension
du module et du facteur de dispersion Kf
5.2.2.1.2. Cas de la dispersion de la
capacitéNous nous intéressons ici à la
dispersion de la capacité. Pendant la charge/décharge les
tensions aux bornes des cellules deviennent
différentes. La cellule qui a une faible capacité Cmin
se charge plus vite que les autres. La tension du module est égale
à la somme des tensions aux bornes de chaque cellule et pendant la
charge/décharge, peut être exprimée par l'équation
5-7.
5-7
U = ? ( ) (
U = ? +
U ESR I
. )
mod sc i
i
i = i = 1 i
c
1
En négligent la chute de tension sur les
résistances ESR, l'équation 5-7 peut être
simplifiée à l'équation 5-8.
U mod ( sc ) ( ) 5-8
= ? U ? ? U c
i=
i i = 1 i
1
La capacité minimum peut être exprimée par
l'équation suivante [149] :
C min = C . (1 + Kc
) 5-9
oü,
oü Kc est le facteur relatif à
la dispersion de la capacité par rapport à la moyenne des
capacités du module.
La chute aux bornes de la cellule ayant la capacité
minimum peut être exprimée par la relation ci-après [149]
:
C
U i = U 5-10
sc mod . n.Cmin
En remplaçant la capacité Cmin
de l'équation 5-9 dans l'équation 5-10, nous pouvons alors
trouver le nombre de cellules n en série (cf. eq. 5-11).
n=
U 1
mod . 5-11
Usci +
1 K c
Comme dans le cas de dispersion de la résistance de
fuite, nous présentons sur la figure 5-4 le nombre de cellule n
vis-à-vis de la tension de module pour une dispersion de la
capacité de 0 à -20%. Nous constatons que le nombre de cellules
à placer en série augmente avec la dispersion.
Notons que l'influence de la dispersion de la résistance
de fuite sur le nombre de cellules n est plus importante que celle
liée à la dispersion de la capacité.
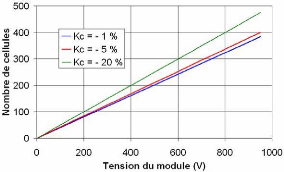
Fig. 5-4 : Nombre de cellules en fonction de la tension
du module et du facteur de dispersion Kc
5.2.2.1.3. Cas de la dispersion de l'ESR
La dispersion sur l'ESR n'est pas étudiée car ce
paramètre influence peu les différences de tension entre chaque
cellule.
5.2.2.2. Différence de température entre
les cellules du module
Les résultats expérimentaux montrent que les
températures sur les cellules d'un même module sont
non-homogènes [104, 150]. Ceci est dû à diverses raisons
comme la nonhomogénéité de la ventilation forcée
(cf. fig. 5-5).
èn
è 1

è1 è n
Flux d'aire forcé


Vue de coté Face
Fig. 5-5 : Exemple de gradient de température
dans un module de supercondensateurs
La dispersion en température des cellules même
avec une faible valeur peut conduire à des tensions de cellules non
égales à long terme, car la résistance ESR et
l'autodécharge varient considérablement en fonction de la
température.
5.2.2.3. Effet de non-similitude du vieillissement sur
les cellules du module
Nous avons vu auparavant que le vieillissement a un effet
direct sur les paramètres internes du supercondensateur : augmentation
de l'ESR, de l'autodécharge et aussi diminution de la capacité.
Des essais de vieillissement ont été réalisés avec
la même tension mais avec une différence de température de
5 °C. Les résultats de ces essais ont montré qu'une faible
augmentation de la température conduit à des vieillissements
très différents sur les cellules. Le même
phénomène peut apparaître en cas de dispersion de la
tension de cellules même en l'absence de surtension (cf. §
5.2.2.5).
| 


