5.2.3. Performance du circuit d'équilibrage de
tension
La tolérance sur les paramètres des cellules de
supercondensateur peut provoquer une surtension durant la
charge/décharge. Par conséquent, il est indispensable de
réduire la valeur de la charge délivrée à ces
composants. A défaut, la surtension qui apparaît localement sur
ces composants peut engendrer so it la dégradation progressive de la
cellule qui affecte la durée de vie de ce composant, soit la destruction
du composant (l'électrolyte organique dans la cellule
commence à se décomposer, produisant des produits
gazeux ainsi qu'une accumulation de pression jusqu'à la destruction du
composant).
Pour éviter ce phénomène, des circuits
d'équilibrage sont ajoutés aux supercondensateurs, afin
d'équilibrer les tensions et de redistribuer les surtensions sur les
cellules [151-153]. Ces circuits permettent d'optimiser l'énergie
stockée [1 51] et de prolonger la durée de vie des
supercondensateurs.
L'étude des différents systèmes
d'équilibrage nous conduit à proposer la définition de
concepts permettant de les comparer en vue de sélectionner le
système le plus performant et le plus fiable.
5.2.3.1. Définition du rendement
énergétique des systèmes d'équilibrage
Afin d'évaluer la performance des systèmes
d'équilibrage en terme d'énergie, nous définissons le
rendement énergétique du circuit d'équilibrage d'un module
par la relation 5-12. Il donne le pourcentage d'énergie stockée
dans les supercondensateurs à la fin de l'équilibrage par rapport
à l'énergie stockée au début d'équilibrage
[154].
n n
i
? W i - ? W eq
i = 1 i = 1
ç = 5-12
n
? Wi
i= 1
où,
Wi est l'énergie utile stockée dans la
cellule i (égale à l'énergie fournie par la
source d'alimentation au supercondensateur moins celle WESR
dissipée dans la résistance ESR),
Weqi est l'énergie dissipée dans le
circuit d'équilibrage lié à la cellule i.
5.2.3.2. Détermination de l'espérance de
vie d'un module
Les supercondensateurs possèdent un nombre de cycles
de charge/décharge très important par rapport aux accumulateurs
classiques. Il s'agit en effet d'une technologie mettant en oeuvre des
phénomènes sans modification physique des électrodes
(théoriquement pas de réaction d'oxydoréduction).
Cependant, l'espérance de vie des supercondensateurs est réduite
pour des températures ou/et des tensions élevées, etc. Il
est donc important d'établir un modèle qui permet d'estimer
l'espérance de vie pour différentes conditions de tension et/ou
de température.
Les processus faradiques dans les supercondensateurs
engendrant un vieillissement sont accélérés par deux
contraintes principales la tension et la température. Comme le montre
la
figure 5-6, le vieillissement du supercondensateur est fonction
de la tension et la température de fonctionnement.
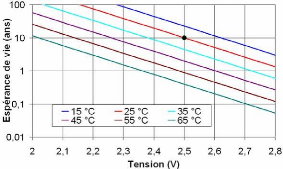
Fig. 5-6 : Espérance de vie du
supercondensateur en fonction
de la tension et la température pour un
composant d'EPCOS (2,5 V ; 65 °C) [19]
Nous pouvons constater d'après de cette courbe que
l'espérance de vie du supercondensateur aux valeurs nominale (2,5 V et
25 °C) est de 10 ans.
U è
( + )
L'espérance de vie Texp s'exprime par
une fonction exponentielle de la tension U et de la température
è (c.f. eq. 5-13) [155] suivant la loi d'Eyring [156, 157].
5-13
exp ( , ) .
è = C t e v
C C
T U è
où,
Ct v, et Cè sont des
constantes de vieillissement qui peuvent être d
, C éterminées à partir de
la figure 5-6 : Ct =1,46.10 ans, Cv
= -149 mV, Cè = -12,4 °C.
9
A côté de l'espérance de vie, un facteur
de dégradation peut être utilisé pour une évaluation
de l'espérance de vie avec des conditions variables (cf. eq. 5-14). La
valeur de ce facteur varie de 0% à 100% (pour les composants vieillis
(la capacité a diminué de 20% et l'ESR de 100%) [124].
dã
|
1
= dt 5-14
T u t
( ( ) ( ))
+ è t
exp
|
|
A partir d'une dégradation initiale ã0 et
l'intégration de l'équation 5-14 d'un état initial
t0 à un état t, nous pouvons calculer la
dégradation instantanée.
t 1
ã = ? dt + ã
5-15
0
t 0 T u t + t
exp ( ( ) è ( ))
L'espérance de vie moyenne Tav pour
un profil de la tension u(t) et une dynamique de la
température è(t) peut être estimée par
l'équation 5-16.
t t
Tav
- 0
( ( ), ( )) u t t
è = 5-16
t 1
dt
? T u t t
t 0 ( ( ) , ( ))
è
exp
Dans notre étude, le supercondensateur étant
considéré comme sain initialement la dégradation
présentée par l'équation 5-15 peut être
réduite à celle de l'équation suivante :
t 1
ã = ? dt 5-17
0 T exp (u( t )
è ( t ))
+
Pour un profil donné (u(t),
è(t)) de période Ttot app
liquée durant N périodes, la dégradation du
composant pendant l'utilisation peut être calculée par
l'équation 5-18.
ã = ? dt + ? dt + +
T 2 T NT
tot 1 tot 1 tot 1
0 exp ( ( ) ( )) exp ( ( ) ( )) (1 ) exp ( ( ) ( ))
T u t + è t T u t + è t
+
T - N T T u t t
... ? dt 5-18
è
Comme les dynamiques de u(t) et de è(t)
sont périodiques d'une durée Ttot, les
dégradations provoquées à chaque période sont
égales. Nous pouvons donc écrire :
Ttot 1
ã = N ? dt
5-19
0 exp ( ( ) ( ))
T u t + è t
L'espérance de vie moyenne Tav pour
un profil de u(t) et de è(t) de période
Ttot peut donc être donnée par
l'équation 5-20.
NT tot
T tot
( ( ), è ( ))
u t t=
Tav
= 5-20
1 dt
T T
tot 1 tot
N? dt ?
T u t t
( T u t t
0 exp ( ), ( ))
è 0 exp ( ( ), ( ))
è
Par conséquent, il suffit de calculer la
dégradation liée à un certain profil du courant durant une
période Ttot, pour déterminer
l'espérance de vie.
Le courant de charge/décharge n'est pas pris en compte
directement dans l'estimation de l' espérance de vie, mais son effet sur
l'autoéchauffement (A0) est considéré dans la
détermination de la température du composant 0
(0 = 00 +A0).
Notons que l'espérance de vie totale d'un module de
supercondensateurs est égale à la plus faible espérance de
vie de la cellule la plus critique.
| 


