Etude et modelisation des supercondensateurs

5.4.2. Systèmes d'équilibrage non dissipatifs

Pour pallier aux problèmes des solutions citées précédemment en l'occurrence l'énergie perdue dans le système d'équilibrage, des structures basées sur l'utilisation de convertisseurs statiques permettent de transvaser le surplus d'énergie aux supercondensateurs en surtensions sur les supercondensateurs sous alimentés.

5.4.2.1. Convertisseur Buck-Boost

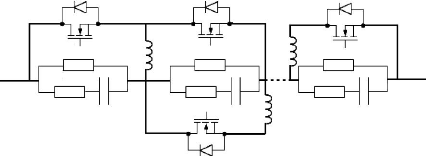
Le principe général est de transférer l'énergie du supercondensateur présentant une tens ion él evée vers celui présentant une tension base, en passant par l'intermédiaire d'une inductance. La figure 5-29 illustre le montage d'un système d'équilibrage qui utilise une association de convertisseurs Buck-Boost (DC-DC) [165, 151].

D1 D2 D_n

ESRl ESR2 C2 ESR_n C_n

Cl

Rf1

T1 T2

Rf2

Rfn

T_n

Usc1 Usc2 Uscn

Umod

Fig. 5-29 : Système d'équilibrage avec convertisseur Buck-Boost associée

5.4.2.1.1. Détermination de la fréquence de découpage et de l'inductance

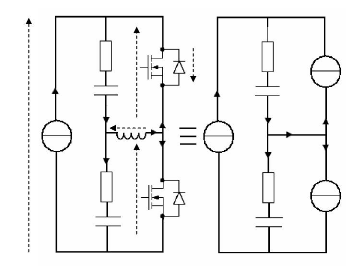
Le principe de ce système consiste à redistribuer l'énergie stockée dans les supercondensateurs par l'utilisation des sources de courant auxiliaire. Afin d'expliquer le fonctionnement du système d'équilibrage et de pouvoir déterminer les paramètres du convertisseur proposé, nous utilisons deux cellules en série, les supercondensateurs SC1 et SC2. En négligeant les résistances de fuite, ces derniers sont simulés par une résistance ESR avec une capacité C en série [166, 165] (cf. fig. 5-30).

(a) (b)

ESRl

Usc1

Cl

iL1

L

I2

ESR2

C2

I

ESRl

Ud

Cl

T1

D1

I

I1

UL iL

I1

iL2

I

2

Usc2

ESR2

T2

D2

C2

2Ieq Ieq

Ieq

Umod

Fig. 5-30 : Principe du système d'équilibrage avec convertisseur Buck-Boost associé [165]

La commande des transistors se réalise selon la logique suivante :

· si Usc1>Usc2 : le transistor T2 est ouvert et T1 commute à la fréquence f,

· si Usc1< Usc2 : le transistor T1 est ouvert et T2 commute à la fréquence f.

Pour égaliser les tensions des supercondensateurs le rapport cyclique des transistors est fixé à 50% ; de ce fait le convertisseur Buck/Boost fonctionne en conduction discontinue. Nous remarquons, par cette logique de commande, qu 'il existe 3 séquences différentes [165].

Dans le cas oil Usc2> Usc1, nous représentons le courant et la tension dans l'inductance L sur la figure 5-31.

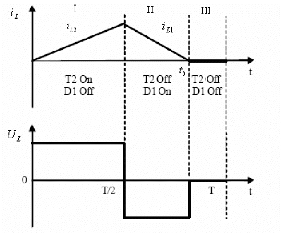
Fig. 5-31 : Séquence du système d'équilibrage
( i_L , U _L ) sont respectivement le courant et la tension de l'inductance L

Ces séquences correspondent aux événements suivants :

· phase I : T2 ON, D1 OFF, les supercondensateurs SC1 se charge avec le courant I, SC2 se charge avec le courant I- iL2 (cf. fig. 5-30),

U sc 2

i i

= 2 = . t

L L 5-45

L

· phase II : T2 OFF, D1 ON, le composant SC1 se charge avec le courant I+ iL1, le supercondensateur SC2 se charge avec le courant I,

5-46

Usc 1 +Ud T Usc2 T

iL ) +

- .( t -

1 L 2 L

2

iL = =

avec U la chute de la tension sur la diode D .

d 1

· phase III : T1 OFF, D2 OFF, SC1 se charge avec I, SC2 se charge avec I.

iL = iL1 = iL2 =0 5-47

A partir de la condition discontinue, nous pouvons déterminer le temps pour lequel le courant de l'inductance s'annule (t0) (cf. eq. 5-48)

.

Usc₂

t₀

Usc ₁

+

Ud

?

= 1+

?

)T

5-48

2

A partir de ces considérations, nous obtenons la relation du courant moyen dans l'inductance (cf. eq. 5-49).

U ? U ?

sc sc

2 2

I = . 1

?? + ?? 5-49

L 8 . .

L f U U

+

? sc d

1 ?

Comme l'illustre la figure 5-30-b, l'expression de l'évolution de la tension de cellule en fonction du courant I et _Ieq en négligeant la chute de tension sur la résistance peut être donnée par le système d'équations suivant :

I + I eq

u sc = . t

u = .t 5-50

sc₂

I-IeqC C

1 2

où,

I est le courant fourni par la source de courant chargeant les supercondensateurs, 2.Ieq est le courant d'équilibrage passant dans l'inductance (cf. fig. 5-30-b).

La valeur et le signe du courant Ieq dépendent de la différence de l'impédance qui existe entre les deux supercondensateurs (SC1, SC2).

Le but du système d'équilibrage étant d'égaliser des deux tensions _(usc1=usc2), ^à p artir de la dynamique de la tension aux bornes des supercondensateurs (cf. eq. 5-50), nous pouvons déduire l'expression du courant _Ieq (cf. eq. 5-51).

I = c

.I 5-51

eq K

-- 2 - K_c

K_c étant le facteur de dispersion sur la capacité.

L'inductance L et la fréquence (f =1/T) de découpage sont déterminées p our obtenir une

valeur moyenne du courant dans l'inductance égale à _2Ieq. En remplaçant le courant moyen de l'inductance donné par l'équation 5-49 par _2Ieq, nous obtenons la formule suivante :

L . f = U sc 2 - 2 - Kc .?1 + sc 2?5-52

Usc1 + U_d

1 6.I Kc

U ?

Par conséquent, en remplaçant les paramètres (I, K_c, U_sc, Ud = 0,3 V) donnés précédemment dans l'équation 5-52, nous obtenons la valeur de l'inductance et de la fréquence de découpage. Par exemple, nous trouvons pour le supercondensateur étudié BCAP010 ; f =10 kHz, L =0,5 uH.

Nous montrons sur la figure ci-dessous la carte de ce circuit d'équilibrage vendu par le fabricant MAXWELL.

Fig. 5-32 : Photo du convertisseur Buck-Boost

5.4.2.1.2. Simulation du module de supercondensateurs

Nous avons simulé le module de supercondensateurs (SC1+SC2) avec ce système d' équilibrage sous Simplorer pour une application à rapport cyclique élevé (cf. fig. 5-7). Les résultats sont présentés sur la figure 5-33. Ils montrent que la tension aux bornes des supercondensateurs s'équilibre très rapidement. C eci permet d'obtenir une espérance de vie et un rendement énergétique élevés (19 ans ; 92%). Nous remarquons que ce système

d'équilibrage améliore le rendement énergétique et qu'il prolonge l'espérance de vie du module de supercondensateurs par rapport aux autres systèmes d'équilibrage.

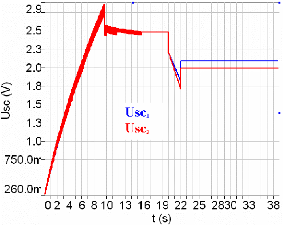
Fig. 5-33 : Tension aux bornes des supercondensateurs pendant l'équilibrage

Cependant, l'effet de la transmission d'énergie par les supercondensateurs peut devenir un inconvénient en terme d'énergie dissipée, lorsqu'un grand nombre de supercondensateurs sont en série.

L'inconvénient principal de ce circuit est son coût très élevé (pratiquement le même coût qu'un supercondensateur) [55].

5.4.2.2. Convertisseur Flyback à secondaires distribués

Cette solution est basée sur le transfert de l'énergie du supercondensateur ayant une tension élevée directement vers celui ayant la tension la plus basse. La figure 5-34 illustre le montage de ce système : un convertisseur statique principal centralisé (flyback multi-sorties) est lié avec un transformateur. Ce convertisseur fonctionne dès qu'une différence de tension est détectée, le transistor T conduit d'abord, permettant au primaire du transformateur de stocker l'énergie. Par la suite cette énergie magnétique va être distribuée au s econdaire du transformateur relié au supercondensateur présentant la tension la plus basse lorsque le transistor est ouvert (l'énergie stockée entraîne la conduction des diodes au secondaire) [151].

5. Evaluation des performances des modules de supercondensateurs

N T

p

i1

D1

Ns1 Ns2

Rf1

D2

i2 i_n

Rf2

D_n

Rfn

Nsn

n

ESRl ESR2 ESR_n

C C2 C

l

Usc1 Usc2 Uscn

Umod

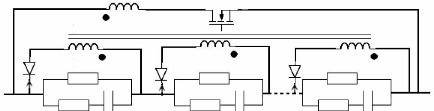
Fig. 5-34 : Système d'équilibrage Convertisseur Flayback à secondaires distribués

5.4.2.3. Convertisseur Forward à bobinage distribués

Une autre solution combine les deux circuits décrits précédemment. L'énergie est transférée directement sans passer par des supercondensateurs intermédiaires.

La figure 5-35 montre le schéma de ce système d'équilibrage. Dès qu'une différence importante de tension entre les supercondensateurs est détectée, le transistor correspondant est fermé. L'énergie va alors passer vers les autres supercondensateurs via les diodes et le transformateur. [151].

i1

N1

ESRl

Cl

Rf1

N D

D2

T T

1 2

Rf2

D1

i2

N2

ESR2 ESR_n

C2 C_n

i_n

N_n

Rfn

D_n T_n

Usc1 Usc2 Uscn

Umod

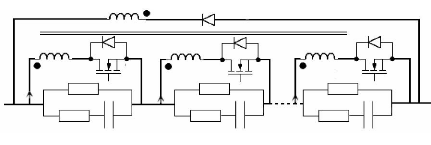
Fig. 5-35 : Système d'équilibrage avec convertisseur Forward à bobinage distribués

Les deux dernières solutions équilibrent les tensions instantanément, comme la solution présentée dans le paragraphe 5.4.2.1. La simulation du dernier système d'équilibrage et pour le module des supercondensateurs présenté auparavant est montrée sur la figure 5-36. Les ré sultats de ces dernières solutions sont relativement proches de ceux de la solution pour le système présenté au paragraphe 5.4.2.1, car nous avons simulé le transformateur par son

modèle idéal. Cependant, les pertes dans le transformateur sont assez importantes. Elles diminuent fortement le rendement énergétique du système global. Les deux dernières solutions ne sont pas employées avec les supercondensateurs car elles sont coûteuses en termes de composants magnétiques et de com nt.

posa

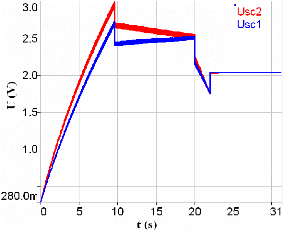
Fig. 5-36 : Evolution de tension aux bornes des supercondensateurs du système d'équilibrage ci-dessus

Il existe encore d'autres solutions d'équilibrage que celles que nous avons exposées [160, 167-169] mais celles-ci sont très complexes et coûteuses. Elles sont donc très rarement utilisées.