Etude et modelisation des supercondensateurs

5.4. Etude comparative de systèmes d'équilibrage

Nous avons vu que la mise en série des supercondensateurs ayant différents paramètres conduit à un déséquilibre de leur tension. Nous présentons dans la suite différents types de systèmes d'équilibrage. Ces systèmes d'équilibrage sont de deux concepts : les circuits dissipatifs et non dissipatifs.

5.4.1. Systèmes d'équilibrage dissipatifs

La solution d'équilibrage dissipative consiste à dissiper une partie de l'énergie stockée dans le supercondensateur à tension élevée. La dissipation de cette énergie excessive ramène la surtension à une valeur de fonctionnement correcte.

5.4.1.1. Système d'équilibrage passif

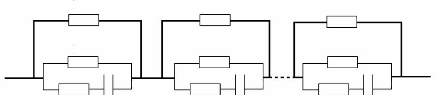
Dans la solution passive, nous plaçons en parallèle aux bornes de chaque cellule des résistances d'équilibrage d'une valeur _Req comme représenté par le schéma sur la figure 5-13 [160, 154]. Le mécanisme de ce type d'équilibrage est simple par son principe : un courant parcourt toujours la résistance d'équilibrage connectée à ses bornes. Plus la tension est forte

plus le courant dans la résistance d'équilibrage est important, ce qui permet d'homogénéiser les tensions aux bornes des différents composants.

Req1 Req2 Reqn

Rf1

Rf2 Rfn

ESRl ESR2 ESR_n

Cl C2 C_n

Usc1 Usc2 Uscn

U_mod

Fig. 5-13 : Module de supercondensateurs avec un système d'équilibrage passif

Nous définissons le facteur d'équilibrage _Keq par la relation 5-23. Ce dernier donne la proportionnalité de la résistance d'équilibrage _Req par rapport à la moyenne des résistances de

fuite R f . D'après la référence [149], sa valeur peut être comprise entre 5% à 10%.

R eq

K = 5-23

eq

R_f

5.4.1.1.1. Calcul du nouveau facteur de dispersion de la résistance de fuite

Nous montrons dans ce paragraphe l'effet de l'emploi des résistances d'équilibrage R_eq aux bornes des supercondensateurs sur la dispersion de ses paramètres. Pour simplifier l'analyse, la dispersion de la résistance d'équilibrage est négligée.

Dans le cas de la dispersion de la résistance de fuite, la résistance équivalente R_pmax des deux résistances en parallèle Rfmax (la plus élevée) et R_eq peut être calculée par la formule suivante :

R R

. R . (1 )

eq f + K

eq f

max

R = = 5-24

max R R

+ K K

+ +

eq f eq f

max

1

p

En raison du nombre n de cellules en série élevé, la moyenne des résistances (R_p) en parallèle peut être approximée avec une faible erreur comme suit :

1 nn R R R R

1 e f

. .

q eq f R

i eq

R = ? =

R =

p ? ?

p 5-25

n i n 1

1 1 R R

i + + K +

= i = eq f R R

eq f eq

i

En considérons les résistances d'équilibrage, un nouveau facteur liée à la dispersion de la résistance de fuite peut être défini par l'équation suivante :

R -R

p p

max

K 5-26

f ' =

R p

d'où, en considérant les équations 5-24, 5-25 et 5-26 :

K K

f eq

.

K f K K

' = 5-27

+ + 1

f eq

Nous montrons sur la figure 5-14 le facteur de dispersion (calculé par l'équation 5-27) en fonction du facteur d'équilibrage pour certai es valeurs du facteur de dispersion de la

n

résistance de fuite Kf. Nous remarquons que l'utilisation d'une résistance d'équilibrage diminue largement la dispersion de la résistance de fuite et par conséquent le nombre de cellules requis en série pour une tension donnée (cf. eq. 5-6). En conclusion, pour un facteur d'équilibrage faible (entre 5% à 10%) la dispersion peut pratiquement disparaître entre les cellules d'un module. La durée de vie des cellule s est alors quasiment égale (si les différences de température entre cellules sont exclues).

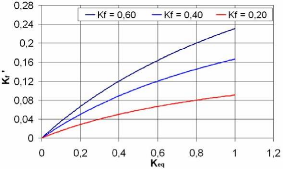
Fig. 5-14 : Evolution de la dispersion de la résistance en fonction du facteur d'équilibrage

5.4.1.1.2. Calcul du temps d'équilibrage

Dans le cas d'une dispersion de la capacité et de la résistance de fuite, le calcul de la performance du système d'équilibrage est difficile et dépend du profil de courant. Nous nous proposons donc de le simuler.

Définissons un nouveau paramètre lié à l'équilibrage à savoir le temps d'équilibrage. Nous distinguerons en fait deux temps d'équilibrage lors de l'étude de ces systèmes. Le premier est le temps Teq pour que les tensions instantanées des cellules du module s'égalent. Le deuxième le temps TU est le temps nécessaire pour que la tension aux bornes d'une cellule présentant une surtension atteigne la tension nominale UN.

Dans les applications ayant un rapport cyclique bas, les temps d'équilibrage sont principalement dûs à la valeur de la capacité du supercondensateur et à la résistance d'équilibrage. Reprenons le module présenté dans le paragraphe 5.2.1 et considérons seulement la dispersion de la capacité. Les résistanc es ESR des différents composants sont négligées.

En fin de la charge, la tension aux bornes de la capacité C2 peut être exprimée en fonction de la tension de la capacité C1 et du facteur de la dispersion K_c à partir de la loi de la conversation de charge par la formule suivante :

U sc = Usc 1 5-28

°' 1 + K c

02

Au moment de l'équilibrage (temps Teq), les tensions des cellules sont égales et peuvent être écrites par le système d'équations suivant en remplaçant la résistance R_p par sa valeur de l'équation 5-25 :

usc ( _eq)= U _s. .exp _1T eq =U

T

.

R_p C

[ Jsc01.exp [- T _eq. (1 + K eq 5-29

)j

Req. C

? T ? ? T + K ?

eq . (1 )

eq eq

u T

( ) = U . exp ?? - ?? = U . exp ?? - ?? 5-30

sc₂ eq sc sc

02 02

R C K

. (1 )

+ R C K

. . (1 )

+

? p C ? ? eq C ?

A noter que les deux tensions ci-dessus sont données sans la dispersion sur les résistances de fuite.

Le temps d'équilibrage peut être obtenu par l'équation ci-après en égalisant les deux dernières équations et en considérant l'équation 5-28 :

eq 5-31

ln(1 ) . (1 )

+ K + K

c c

T = . .

C R

eq K _c. (1 + Keq)

Dans certaines applications, il n'est pas nécessaire d'équilibrer les tensions instantanées des cellules mais seulement de réduire la surtension _Umax à la tension nominale. Ce dernier équilibrage permet de limiter la dissipation d'énergie dans les systèmes d'équilibrage. Si le supercondensateur SC2 de capacité C2 présente une surtension _Umax, nous pouvons identifier l'instant TU où la tension nominale est atteinte à partir de l'équation suivante :

?T.? ? T . (1 )

+ K ?

U U eq

1 1

u T U

( ) = . exp ?? - ?? = U . exp ?? - ?? = U 5-32

sc U max max N

2 ¹ R C R C K

. (1 )

+

? p 2 ? ? eq c ?

D'où,

eq

T (1 ) . ln ^max .

? U ? R

= + K ? ? . C

U c 5-33

? U 1 + K

N ? eq

Nous montrons sur les figures 5-15-a et b ces temps en fonction de la résistance d'équilibrage et pour différents facteurs de dispersion. Il est bien évident que le temps TU requis pour atteindre la tension nominale est inférieur à celui d'équilibrage _Teq. Plus le facteur de dispersion de la capacité est élevé, plus les temps requis _Teq et TU pour atteindre l'équilibrage sont faibles. Ceci s'explique car avec une forte dispersion sur le facteur K_c, la capacité correspondante est faible et donc la constante de temps de charge ou décharge est faible.

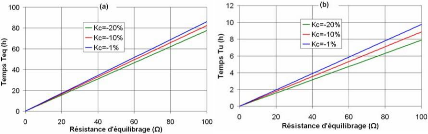
Fig. 5-15 : Temps d'équilibrage en fonction de la valeur de résistance d'équilibrage

Ces résultats sont obtenus avec comme seule dispersion sur les paramètres du composant la dispersion sur la capacité.

Dans le cas d'application où le rapport cyclique est bas, il est préférable de considérer une dispersion sur la capacité (K_c) et sur la résistance de fuite (Kf). Les tensions des cellules sont alors exprimées par les équations 5-34 et 5-35.

? +

t K

. (1 ) ?

eq

u t U

sc 1 ( ) 01 . exp

= ?? - ??

sc 5-34

R C

? eq . ?

?t K K
. (1 + eq f

+ ) ?

u t U

sc 2 ( ) 02 . exp

= ?? ??

sc - 5-35

R C K

. . (1 ) . (1 )

+ + K

? eq C f ?

De la même manière que ci-dessus, nous trouvons les nouveaux temps d'équilibrage (cf. eq. 5-36 et 5-37).

ln(1 + K_c ) . (1+ K _f + K _c K_c .Kf ^Teq K K K K K K K K

) .C. R

eq 5-36

+ . + . + _eq K _c . K f

.

c + c f eq f eq c

.

? U ?R

max eq

T = + +

(1 K K K K

+ ? ? . C

U c f c f

. ) . ln . 5-37

1

eq

U +K +Kf

La proportionnalité des deux temps d'équilibrage (sans (Teq1) et avec la dispersion (Teq2) sur la résistance de fuite) est donnée par l'équation 5-38. La figure 5-16-a donne cette relation en fonction du facteur de la dispersion avec K_c=-20%. Elle démontre que la dispersion de la résistance de fuite (avec la dispersion de la capacité) ralentit l'équilibrage des tensions.

Ceci peut être obtenu de la même façon pour le temps d'équilibrage TU (cf. eq. 5-39 et fig. 5- 16-b).

K_c . (1 + K _f + K _c + Kc.

)

5-38

K _f ) . (1 +K

eq

T eq 2

K _c + K_c . K _f + K_eq + K_eq . K_c+

.K f

Keq .K _c . K _f ) . (1 + K_c

T eq 1 (

)

T U 2

)

5-39

eq

1 + K _c +Kf.K

c + K_f ) . (1 + K

TU1 1 + K f +Keq )(1 +K_c )

où,

TU1 ^et _TU2 sont les temps d'équilibrage respectivement sans et avec la dispersion sur la résistance de fuite.

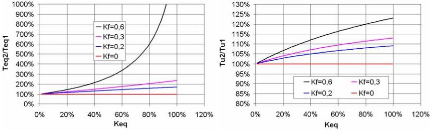
(a) (b)

Fig. 5-16 : C omparaison des temps d'équilibrage sans et avec la dispersion de résistance de fuite

La dispersion de la résistance de fuite augmente le temps d'équilibrage et peut donc réduire l'espérance de vie du composant et du module.

Dans les applications ayant un rapport cyclique élevé, il est difficile d'équilibrer la tension instantanée. Nous définissons donc un nouveau temps d'équilibrage correspondant au temps pour équilibrer les tensions moyennes.

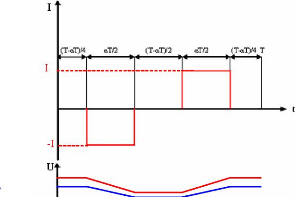
Nous représentons sur la figure 5-17 le profil du courant et la réponse en tension d'un module de supercondensateurs utilisé dans une application avec rapport cyclique élevé. Pour une période T, le module est chargé à courant constant I pendant un temps áT/2 et déchargé pendant le même temps.

Umax

(1+Kc)Umax

-Usc2
-Usc1

Fig. 5-17 : Profil général du courant

Nous pouvons déduire le temps d'équilibrage des tensions moyennes à partir de la définition

de la valeur moyenne. En considérant des valeurs de capacité fixe (non dépendante de la tension), les tensions moyennes sans système d'équilibrage peuvent être écrites par les équations ci-dessous :

1

=

Usc

U sc 2

). C

5-40

á +

T I U

4 . . (1 + K c

max

4 . C

- á + max +

T I U

4 . . (1 c ).

K C

5-41

K_c )

4 . . (1

C +

Les évolutions des tensions moyennes pendant l'équilibrage sont données par le système d'équations suivant :

- á

. exp

t

5-42

T I U

+ 4 . max . (1 ).

+ K C

u =

sc 1

-

c

4 . C .

R C
p .

u

2

á T I U

+ 4 . max . (1 + K c

). C

. exp

? t ?

?? - ??

. . (1 )

+

? ?

c p c

5-43

sc 4 . . (1 )

C K

+ R C K

A l'équilibre, les deux tensions moyennes exprimées ci-dessus sont égales. D'où, nous pouvons calculer le temps d'équilibrage par l'équation 5-44.

eq 5-44

ln(1 ) . (1 )

+ K + K c c

T = . .

C R

eq K K

c . (1 + _eq )

A titre de comparaison, nous constatons que les deux temps d'équilibrage, celui de la relation 5-31 et de la relation de 5-44 sont identiques.

Dans le cas où la capacité et la résistance de fuite du supercondensateur SC2 sont dispersées, nous trouvons un temps d'équilibrage des tensions moyennes égal à celui donné par la relation 5-36.

5.4.1.1.3. Résultats de la simulation des applications

Nous comparons sur la figure 5-18-a et b l'espérance de vie, le rendement énergétique et le temps d'équilibrage pour les de ux profils du courant avec un rapport cyclique élevé (cf. fig. 5- 7 et 5-9). Ces résultats sont calculés par le logiciel Simplorer (méthode de Monte Carlo) pour Ttot= 1 h et K_c= -20%. Nous remarquons que les deux profils énergétiquement identiques

donnent des résultats identiques.

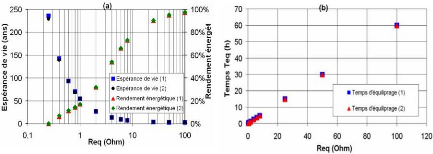
Fig. 5-18 : Comparaison de performance des applications à rapport cyclique ^élevé(1) profil de fort courant de charge/décharge (cf. fig. 5-7), (2) profil du projet THALES (cf. fig. 5-9)

Nous montrons sur la figure 5-19 l'espérance de vie vis-à-vis de la dispersion de la capacité K_c du supercondensateur. Nous remarquons que, quelle que soit la résistance de fuite, l'espérance de vie est supérieure à celle sans système d'équilibrage et qu'une résistance d'équilibrage faible, qui va rapidement supprime les surtensions, améliore cette espérance de vie.

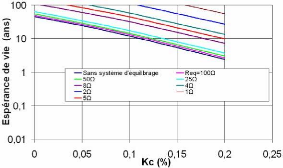
Fig. 5-19 : Espérance de vie en fonction du facteur de dispersion avec système d'équilibrage passif

D'après ces résultats pour des applications à rapport cyclique élevé, nous constatons qu'une résistance autour de 5 ? donne un résultat équilibré : une espérance de vie de l'ordre de 10 ans et un rendement énergétique de l'ordre de 60%. Nous représentons sur la figure 5-20 la tension aux bornes des supercondensateurs pour cette valeur de résistance pour l'application à fort courant (cf. fig. 5-7).

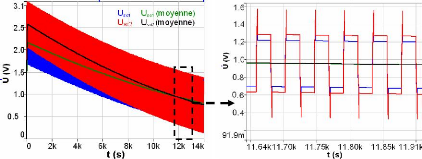
Fig. 5-20 : Tension aux bornes des supercondensateu avec une résistance d'équilibrage de l'ordre de 5?

rs

Notons que les performances de ce type d'équilibrage peuvent varier suivant le profil de l' application et que les résultats présentés sont donnés à titre indicatif.

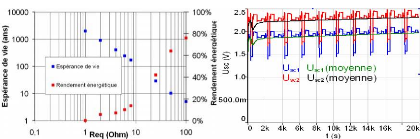
Nous représentons sur la figure 5-21-a la performance du système d'équilibrage vis-à-vis de la résistance d'équilibrage pour une application à rapport cyclique bas (cf. § 5.3.1.2). Nous présentons sur la figure 5-21-b le profil de la tension aux bornes de supercondensateurs résultant des données du paragraphe 5.3.1.2 et pour une résistance d'équilibrage de 50 ?. D'après ces résultats, nous constatons qu'une telle valeur de résistance d'équilibrage de 50 ? est capable de limiter la tension au-dessous de sa valeur nominale et donne une espérance de vie et un rendement acceptables (espérance de vie de l'ordre de 10 ans et rendement de l'ordre de 60%).

(a) (b)

Fig. 5-21 : Résultats de la simulation d'une application ayant un rapport cyclique bas

Ce type d'équilibrage passif est intéressant dans les applications ayant un rapport cyclique bas car sont coût est faible et les résistances d'équilibrage de relativement forte valeur conviennent [161]. Pour ce type d'application, nous n'étudierons pas les autres systèmes d'équilibrage plus coûteux

5.4.1.2. Diodes Zener

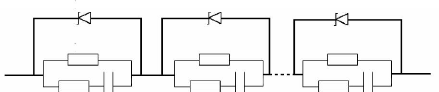
La deuxième solution consiste à utiliser des diodes Zener, en remplacement des résistances dans le système d'équilibrage passif [155]. Celles-ci doivent équilibrer la tension des supercondensateurs selon leur tension Zener. La figure 5-22 représente le circuit équivalent de ce système, dans lequel les diodes Zener sont liées en parallèle aux supercondensateurs. Le mécanisme de cet équilibrage est lié toujours à une perte d'énergie dans les diodes Zener. La difficulté majeure de ce système d'équilibrage est essentiellement de trouver les diodes Zener qui conviennent pour une application donnée comme les applications présentées précédemment [154].

D1 D2 D_n

Rf1

Rf2 Rfn

ESRl Cl C2

ESR2 ESRn Cn

Usc1 Usc2 Uscn

Ucn

Fig. 5-22 : Système d'équilibrage à diodes Zener

5.4.1.3. Résistances commandées

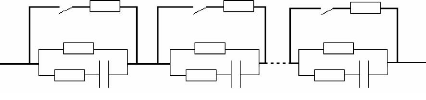
Dans ce système d'équilibrage, un interrupteur actif est mis en série avec la résistance d'équilibrage. Ce dispositif est relié en parallèle à chacune des cellules du supercondensateur (c.f fig.5-23). Lorsque la tension du composant dépasse une valeur donnée, l'interrupteur est fe é, ce qui permet à un courant de parcourir la résistance d'équilibrage (comme dans le cas

rm

de l'équilibrage passif). Ensuite, l'interrupteur est ouvert lorsque la tension aux bornes de la cellule surveillée revient à une valeur de référence [56, 162, 153].

S 1 Req1 S2 Req2 S_n Reqn

ESRl ESR2 ESR_n

Cl C2 C_n

Rf1 Rf2

Rfn

Usc1 Usc2 Uscn

Umod

Fig. 5-23 : Système d'équilibrage à résistances commandées

C

e système d'équilibrage se compose d'un circuit actif principal comprenant un dispositif actif de commutation tel qu'un transistor bipolaire ou MOSFET associé à la résistance d'équilibrage, un circuit de commande, et un autre de détection (cf. fig. 5-24). La commande de l'interrupteur est choisie de la telle façon qu'un minimum d'énergie soit dissipée dans les résistances d'équilibrage. L'interrupteur est fermé quand la tension du supercondensateur dépasse une valeur seuil. A titre d'exemple, le transistor (IRLI3705NPbF ; VDSS= 55 V ; R

DS(on)=0,01? ; ID=52 A) du fabricant International Rectifier a été choisi dans le système de la figure 5.24).

Fig. 5-24 : Schéma de la carte électronique d'équilibrage et sa photo [162]

5.4.1.3.1. Résultats de la simulation des applications ayant un rapport cyclique élevé

Nous présentons sur les figures 5-25-a et b les résultats de la simulation des deux profils du courant à rapport cyclique élevé (cf. fig. 5-7 et 5-9). Nous remarquons que cette solution d'équilibrage permet de contrôler l'énergie dissipée dans les résistances d'équilibrage, ce qui améliore fortement le rendement énergétique du système d'équilibrage (ç ? 87%).

Sur les figures 5-25-a et b, la résistance d'équilibrage _Req est limité à 5 ? car au-delà le temps d'équilibrage (TU) est supérieur au temps total simulé (Ttot).

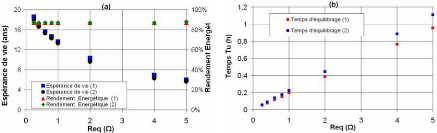
Fig. 5-25 : Comparaison de performanc des applications à rapport cyclique bas
e
avec les résistances commandées

L'intérêt de cette solution est de prendre des valeurs faibles de résistances d'équilibrage pour réaliser l'équilibrage le plus rapidement possible, car le rendement énergique ne peut pas descendre au-dessous d'une valeur limite. Cependant, pour des considérations de puissance dissipée dans cette résistance, la valeur de cette dernière ne pourra pas être trop faible.

Une résistance d'équilibrage de l'ordre de 2 ? peut donc, en plus d'un rendement élevé, assurer une espérance de vie d'environ 10 ans pour les deux profils, quelque soit la dispersion de la capacité (cf. fig. 5-25). La figure 5-26 montre la tension aux bornes des supercondensateurs (SC1 et SC2) avec un facteur de dispersion (KC) de -20% pour des résistances commandées de 2 ?.

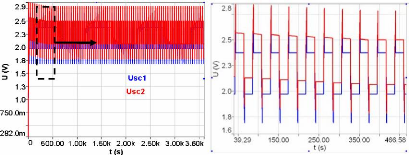
Fig. 5-26 : Tension aux bornes des supercondensateurs pour résistances commandées de 2 ?

Nous pouvons conclure que le système d'équilibrage à résistances commandées e st bien adapté aux applications à rapport cyclique très élevée [163].

La commande du transistor peut être réalisée par différentes méthodes. A titre d'exemple, dans notre exemple, nous fermons l'interrupteur quand la chute de la tension U_c sur la capacité du supercondensateur dépasse la valeur nominale limite ; U_c est donc la tension du supercondensateur moins la chute de tension sur la résistance ESR . Ceci permet d'améliorer la

performance du système d'équilibrage pour les applications à rapport cyclique élevé et de réduire le temps d'équilibrage TU.

La validation expérimentale de l'estimation de la résistance ESR par un circuit supplémentaire connecté en parallèle au supercondensateur est envisageable [164].

5.4.1.3.2. Nouvelle génération de résistances commandées

Nous pouvons trouver différentes configurations du circuit d'équilibrage avec résistances commandées. Le fabricant MAXWELL propose actuellement le circuit d'équilibrage donné sur la figure 5-27. Ce circuit se place entre deux supercondensateurs. Pour un nombre de cellules n, il faut n-1 circuits d'équilibrage. Son principe est basé sur la comparaison entre la tension des deux cellules de supercondensateurs ; le signal à la sortie du comparateur commande les transistors complémentaires Q1 et Q2 [55]. Il y a deux types de ces circuits selon la valeur désirée du courant d'équilibrage ; à faible et à fort courant.

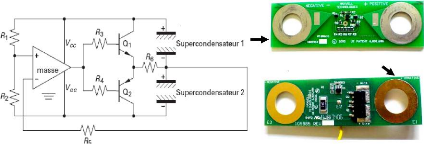
Circuit avec faible
courant d'équilibrage

Circuit avec fort
courant d'équilibrage

Fig. 5-27 : Schéma de principe d'un circuit d'équilibrage à résistance commandée de MAXWELL [55]

Le transistor Q1 est fermé quand la tension aux bornes du supercondensateur 1 est supérieure à celle du supercondensateur 2 et inversement.

La commande de ce type de circuit est très simplifiée, ce qui impacte le prix de celui-ci. L'av antage principal de ce système est qu'il permet d'équilibrer les tensions moyennes assez

r pidement et de stabiliser leur valeur avec le temps. A long terme cela peut aider à limiter a

l'apparition de la surtension sur le composant critique. La fi gure 5-28 présente la tension aux bornes des supercondensateurs avec ce type de commande (KC=-20%).

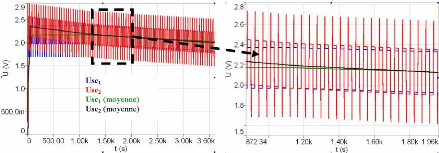
Fig. 5-28 : Tension aux bornes des supercondensateurs avec une résistance d'équilibrage de 5,5 ?

5.4.1.4. Transistors MOSFET linéaires

Nous pouvons aussi utiliser comme système d'équilibrage des MOSFET en remplacement du transistor et de la résistance d'équilibrage des circuits présentés précédemment. L'énergie de la surtension est alors dissipée dans la ré sistance interne du transistor. Ce dernier est commandé dans sa zone linéaire. La tension de commande grille source _Vgs est variable et proportionnelle à l'inverse de la surtens ion.