Conception d'un pro logiciel interactif sous r pour la simulation de processus de diffusion

2.4 Approximation la dérive d'un mouvement brownien standard par un bruit blanc gaussien

Un bruit blanc est une réalisation d'un processus aléatoire dans lequel la densité spectrale est la même pour toutes les fréquences, on parle souvent de bruit blanc gaussien, il s'agit d'un bruit blanc qui suit une loi normale de moyenne et variance données.

Définition 2.4 Un processus åt est qualifié de bruit blanc gaussien si : - E(åt) = 0 et E(å2 _t ) = ó2

- åt et å_s sont indépendants ?t =6 s

- åt ~ N(0,ó²)

Par analogie avec le bruit blanc en temps discret, défini comme une suite de variables aléatoires, centrées, du second ordre et indépendants, on cherche à définir {åt}t=0 comme un processus stochastique vérifiant ?t > 0 et ?h > 0 :

- E(åt) = 0

- E(åtåt+h) = ä0(h)

où ä0 est la mesure de Dirac en 0.

Un tel processus n'existe pas. Son idéalisation est la dérivée d'un mouvement brownien standard. Si pour Ät > 0 fixé, on considère le processus

åt =

Wt+Ät -Wt

Ät

Il est facile de montrer grâce aux propriétés données par la définition de mouvement brownien

que :

( ) _(|h| )

1 1 - |h|

E(åt) = 0 et E(åtåt+h) = ¹[0,1]

Ät Ät Ät

Quand Ät -? 0,E(åtåt+h) converge vers ä0(h). Il est donc clair que la dérivée formelle dWt

dt a

les propriétés d'un bruit blanc gaussien. Ce qui justifie l'affirmation concernant l'idéalisation du

bruit blanc. Donc on peut écrire formellement :	åt =	dWt
		dt

2.5 Continuité des trajectoires

Dire qu'un processus aléatoire {Xt,t = 0} est continu c'est, par définition dire que

lim |Xt+h -Xt| = 0 h?0

Selon le type de convergence de cette variable aléatoire, on obtient une continuité plus ou moins forte. La plus faible des notions de continuité est liée à la convergence en loi. Elle est évidement vérifiée. Nous allons démontrer une continuité en probabilité pour le mouvement brownien standard.

Proposition 2.1 Soit å > 0 et {Wt,t = 0} un mouvement brownien standard. On a

1

lim

h?0 h

P(|Wt+h -Wt| > å) = 0

Preuve Soit h > 0, par définition, l'accroissement Wt+h -Wt admet pour loi N(0,h). Donc

1

2 8 1 x2

_hP(|Wt+h - Wr| > å) = h , 2ðhe- 2h dx

8 1 1

å

x

< 2

J e-

E .V22.c h3/2 2h

ie v

1

2h

-

_å2
2h

e

å

h³/²

v

2

=

_vð

Le dernier terme converge vers 0 lorsque h ? 0.

2.6 Régularité des trajectoires

Le mouvement brownien a de nombreuse propriétés dont certaines peuvent être prise comme définition.

Proposition 2.2 Le processus Wt est un processus à accroissements indépendants de fonction de covariance

(s,t) = E(W_sWt) = ó²min(s,t)

Preuve Le mouvement brownien est un processus centré, les accroissements étant indépendants, on a pour 0 = s < t,

E(W_sWt) = E(W_s(Wt -W_s)) +E(W²_s )

= E(W_s)E(Wt -W_s) + var(W_s) = 0 + ó²s = ó²s

et pour 0 = t < s on a,

E(WtW_s) = E(Wt(W_s -Wt)) + E(W²

t )

= E(Wt)E(W_s -Wt)+var(Wt) = 0 + ó²t = ó²t

d'ou : E(W_sWt) = ó²min(s,t).

dx

La fonction BMcov donne une représentation graphique (Figure 2.8) de la fonction de covariance empirique d'un mouvement brownien standard (pour M = 500 trajectoires simulée de taille N = 1000, C = ó2).

R> BMcov(N = 1000, M = 500, T = 1, C = 1)

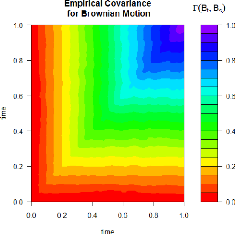
FIGURE 2.8 - Fonction de covariance empirique d'un mouvement brownien standard.

Proposition 2.3 La densité de ÄW = (Wt1 -Wt0,...,Wt_n -Wtn-1) est donnée par

fÄW(x1,...,xn) =	n ? j=1	1 p2ð(tj -tj-1) exp	-x2 j
			2(tj -tj-1)

Proposition 2.4 La densité de W = (Wt1,...,Wt_n) est

f(x1,...,xn) =

n ? j=1

1 p2ð(tj -tj-1) exp

n ? j=1

-(xj -xj-1)^2 2(tj -tj-1)

Proposition 2.5 Pour un mouvement brownien standard (m = 0,ó = 1) et pour tout n, l'espérance

Z +8

E(Wt+h -Wt)²ⁿ = 1

v

-8 x²ⁿe^-x2/^2hdx = 1.3...(2n - 1)hⁿ 2ðh Presque toutes les réalisations du mouvement brownien sont continues (appliquer le théorème 1.1 de Kolmogorov avec c = 3,p = 4 et r = 1).

Proposition 2.6 Soit Wt un mouvement brownien standard. On a presque sûrement,

lim t?+8

sup

Wt vt

= +8 , lim t?0

sup

Wt vt

= +8,

inf ^Wt vt

, lim

t?0

inf ^Wt vt

= -8

= -8,

lim Wt = 0.

t?+8 t

lim

t?+8

et

Preuve Comme pour tout s > 0,

U = lim t?+8	sup	Wt	= lim t?+8	sup	Wt-s-Wt
		vt			vt

cette limite est indépendante de la tribu ó(W_u,u = s) et donc de ó(W_u,u = 0) et par conséquent
d'elle-même. On a soit P(U = +8) = 1 soit P(U = a) = 1. Supposons que la limite sup soit

)atteinte en a. Pour tout b > a, P (^Wt_vt > b ) tend vers 0, mais P (^Wt_vt > b= P(W1 > 0) = 1, Donc

a ne peut être qu'infini. Pour la limite inférieure, il suffit de considérer -Wt. Pour les limites au voisinage de zéro, on considérera le processus Xt = tW1/t, pour établir la dernière formule, on pose s = 1/t et on considère le mouvement brownien Xt = tW1/t, on a Wt/t = sW1/s = X_s ? 0 p.s. puisque Xt est un mouvement brownien standard.

Les deux codes 3 et 4, permettes de vérifier par simulation la proposition 2.6, le mouvement brownien standard est simulée a partir de développement de Karhunen-Loève. La figure 2.9 montre clairement que le mouvement brownien standard est non différentiables, et la figure 2.10 montre que la limite de mouvement brownien standard par rapport au temps tend vers 0 quand t?+8.

FIGURE 2.9 - Le mouvement brownien standard est non différentiables.

FIGURE 2.10 - La limite de mouvement brownien standard par rapport au temps.

Proposition 2.7 Soit 0 = t0 < t1 < ··· < t_n < tn+1 = t une subdivision de l'intervalle [0,t] dont le pas tend vers 0, la variation quadratique converge dans L² vers t

2 L2

V_n = Eⁿk=0(Wtk+1 -Wtk) ---?t Preuve Le calcul de la norme donne

||Vn -t||^2L2 = E		n k=0		(Wtk+1 -Wtk)^2 - (tk+1 -tk)	!2
= E	n k=0		((Wtk+1 -Wtk)^2 - (tk+1 -tk))^2 +E i6=j			E(XiXj)

avec

Xi = ((Wti+1 -Wt_i)² - (ti+1 -ti))

Le produit des termes croisés est nul, car on a pour i < j E(XiXj) = E(E(XiXj)|Ft_j) = E(E(Xi)E(Xj|Ft_j)) = 0 et puisque Wti+1 -Wti est Ft_j-mesurable. Il reste donc

n

||V_n -t||²_L2 = E((Wtk+1 -Wt_k)² _-(tk+1 -tk))²

k=0

Mais les accroissements (Wtk+1 ^--Wtk)²/(tk+1 -- tk) ont même loi que Z², où Z est une variable aléatoire centrée réduite. D'où

n

||V_n --t||²_L2 = E(Z² -- 1)² k=0 (tk+1 --tk)²

< E(Z² -- 1)²t _sup(tk+1 --tk) -+ 0

Proposition 2.8 Si Wt est un mouvement brownien, alors il en est de même pour les processus suivante

(1). Xt = 1aWa2t pour a constante non nulle (invariance par changement d'échelle).

(2). Xt = tW1/t pour t > 0 et X0 = 0 (invariance par inversion de temps).

(3). Xt = WT--t --WT avec T > 0 et t E [0,T] (invariance par retournement du temps). Preuve Il suffit de vérifier que le processus est gaussien et de même covariance que Wt(t A s). Vérifions (1), on a

1

E(X_sXt) = _a2 E(Wa2sWa2t) = a2 min(a²s,a²t) = min(s,t)

1

De mêmee pour (2), on a

E(X_sXt) = tsE(W1/sW1/t)) = tsmin(1/s,1/t)) = min(s,t)

et pour (3), on a

E(X_sXt) = E((WT--ss ^--WT)(WT--tt --WT)))

= E(WT--sWT--t)^--E(WT--sWT)) -- E(WTWT--t)+E(W²T ))

=min( T--s, T--t)-- T+s+t

Sit > s, E(X_sXt ) = T-- t-- T+s+ t =s Sit <s, E(X_sXt ) =T --s--T +s+t =t d'ouu : E(X_sXt) = min(s,t).