Conception d'un pro logiciel interactif sous r pour la simulation de processus de diffusion

4.5 Calculs de l'instant de premier passage

Les instants de premier passage "IPP" jouent un rôle très important en pratique. L'objet de cette étude est de déterminer la densité de probabilité de la variable aléatoire t l'instant de premier passage d'un processus de diffusion Xt. Dans le chapitre 2 la technique des martingales et théorème d'arrêt qui nous a permet de déterminée la loi du temps d'atteinte du mouvement brownien a un point donnée a (le mouvement brownien est un martingale). Dans cette section, on peut utiliser les techniques de la transformée de Laplace, pour déterminer la loi de probabilité de t.

Soit {Xt,t = 0} un processus de diffusion solution de l'équation différentielle stochastique suivante :

dXt = u(t,Xt)dt +a(t,Xt)dWt, X0 = x0 (4.23)

On admet que les coefficients u(x,t) et a(x,t) remplissent les conditions d'existence et unicité de la solution Xt (Chapitre 3 section 3.3.2). Soit D une partie de R que l'on va supposer ouverte et bornée et soit a un élément de D. On défini la variable aléatoire t_a :

t_a = inf{t = 0 : Xt ? aD,Xt = a}

t_a représentant le premier instant où le processus Xt frappe la frontière du domaine D.

8. La fonction PDP permettre de simulée Pearson Diffusions Process. voir help(PDP) pour plus de détails (Package Sim.DiffProc).

4.5.1 IPP d'une diffusion en attraction M ó s=1(Vt)

Dans une première partie, pour le cas s = 1, nous allons effectuer une etude analytique,

afin de determiner explicitement la densite de la variable ô(s=1)

c , cette loi de probabilite permet

d'approximer pour ce modèle, le taux des polluants qui depasse la frontière ?D(0,c). Pour le cas
de s > 1, la simulation est utilisee pour determiner approximativement la densite de la variable

(s>1)

ô_c [2, 4, 6, 7].

Modèle Mós=1(Vt)

L'equation de ce modèle, pour le processus radial Rt, est de la forme :

R^dR0 = a

t = ó22(1R-t Wt

^k)dt + ad ,

{

a > 0, t ? [0, T] (4.24)

Avec k = 2K ó2 pour des raisons de calcul. On utilise l'equation (4.24) pour determiner explicitement la loi de probabilite de ô(1)

c.

La probabilite de transition ft(r|a) represents la densite de Rt avec R0 = a, qui est donne par l'equation de Fokker-Planck retrograde (4.3) :

? ó² ? _ó2 ?2

?t ft(r|a) = (1-k) 2a ?a ft(r|a) + 2 ?a2 ft(r|a) (4.25)

avec la condition initiale f0(r|a) = ä(a - r), où ä(.) fonction de Dirac.

La forme analytique de la densite ft(r|a) peut être explicitement determinee en inversant son transforment de Laplace fë(r;a), qui est la solution de l'equation suivante :

_ó2 ?2 ó2 ?

2 ?a2 fë(r; a) + (1-k) 2a ?a fë(r; a) - ëfë(r; a) = -ä(a - r) (4.26)

Puisque :

a?t ft (rla) =

t

^e

L ( ) ët ?t ft(r|a)dt = - f0(r; a) + ëfë(r; a)

f

0

Une technique standard [39, 5], la solution de l'equation (4.26) pouvoir être formellement ex-prime comme :

-²g1,ë(r)g2,ë(a)

a > r (4.27)

fë(r;a) =

ó2 (g1,ë(r)g⁰2_,ë(a) - g⁰1_,ë(r)g2,ë(a)

),

avec :

)

g1ë(a) = amIm av2ë )

et g2_,ë(a) = a^mH_m

a v2ë

ó ó

avec m = k - ¹₂, I_m et H_m sont respectivement les fonctions de Bessel modifiée [39] de première et seconde ordre, définies par :

Im(z) =

8 ? i=1

, I-m(z) - Im(z) (-1)^i ( z ) 2i+m n et Hm(z) = i!(i+m+ 2 sin(mð) rn+1) 2 I \

On remplace _g1,ë et _g2,ë dans l'équation (4.27), on trouver :

₂2 (a )m+1 _r2³ Hm ^a2ë _Im rv2A a > r (4.28)

,

fë(r; a) =

ó va r ) ó ó

l'inverse de l'équation (4.28), est donnée par :

~ 1 ~_~a ~k _r ~ ~

r3 _-a² + _r2 ~ _ar ~

ft(r|a) = a exp I_m (4.29)

ó²t r 2ó²t ó²t

Maintenant nous définissons la variable aléatoire ô⁽¹⁾ _cpar :

_ô(1)

c = inf{t = 0 : Rt = c, R0 = a}

On a,

f (1) (ë) = E(e^-ë41) |R0 = a) = g2,ë(a)

a = c

ôc g2 _ë (c) ,

Pour des petites valeurs de c, nous obtenons ([5, 6])

(av_ó2ë)^m

fe) (ë) =

2m-1(m)Hm

av2ë)

en inversant (4.30), on trouve l'expression analytique de la densité de probabilité de la variable aléatoire ô(1) c , donnée par :

1 i a2\ m-1 exp ( a2

fôc (1)(ô) = 2(m) 2ó²ô ) 2ó2ô) (4.31)

Le changement de variable :

donne

X=

a^2 ó^2ô

(1 )m
fX(x) = 2 _xm-1_e-2

(m)

d'où, on a :

a2 1)F,41)(ô) = 1 - F(m1/2) (ó2 ô

1 _ 2K 1- 9

avec m = k - 2 2 et (m, 1/2) est la loi gamma.

-- a²

Remarque 4.2 La condition 2K > ó², doit être vérifier (Chapitre 3 section 3.5.1)

(4.30)

ó

Simulation la variable ô(1)

c

La fonction tho_M1 permettre de simulée un échantillonne de taille M = 50 de la variable

aléatoire ô(1)

c . Avec K = 2 etó= 1, le pas Ät = (T-t0)/N, et le c = v = 0.5.

R> tho_M1(N = 1000, M = 50, t0 = 0, T = 1, R0 = 1, v = 0.5, K = 2,

+ R> FPT		sigma =	1)										[1]
0.245	0.037	0.113	0.050	0.060	0.046	0.107	0.182	0.232	0.056	0.032		[12]
0.219	0.085	0.065	0.090	0.032	0.083	0.147	0.065	0.053	0.072	0.073		[23]
0.074	0.040	0.099	0.101	0.177	0.072	0.089	0.198	0.108	0.088	0.058		[34]
0.071	0.181	0.209	0.117	0.082	0.057	0.136	0.078	0.133	0.026	0.121		[45]
0.079	0.331	0.158	0.090	0.091	0.074

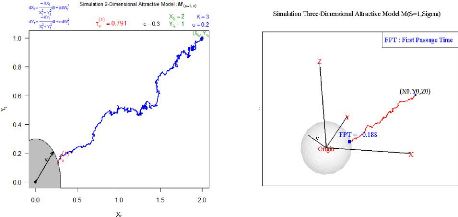
Les deux figures 4.10 et 4.11 donne une illustration de l'instant où le processus Rt frappe la frontière du domaine D. On défini le domaine D par un cercle de rayon c = v = 0.3 (en deux dimensions), et par une sphère de rayon c = v = 0.3 (en trois dimensions).

1

_ô(1)

c

FIGURE 4.10 - L'instant de premier passage du modèle Mó s=1(Vt) en 2-D.

Estimation de la distribution de Y = a2 ó2

FIGURE 4.11 - L'instant de premier passage du modèle Mó s=1(Vt) en 3-D.

R> Y = 1/FPT

R> Ajdgamma(Y, starts = list(shape = 1, rate = 1), leve = 0.95) Profiling...

$summary

Maximum likelihood estimation Call:

mle(minuslogl = lik, start = starts)

Coefficients:

Estimate Std. Error shape 3.5297529 0.68206463 rate 0.2684711 0.05574823 -2 log L: 319.8036

$coef

shape rate

3.5297529 0.2684711

$AIC

[1] 323.8036

$vcov
shape	rate		shape
0.46521216	0.035382963		rate
0.03538296	0.003107865

$confint

2.5 % 97.5 %

shape 2.3624031 5.0474887 rate 0.1731289 0.3925789 R> hist_general(Data = Y, Breaks='Sturges', Law = "GAmma")

R> Kern_general(Data = Y, bw='SJ', k = "gaussian", Law = "GAmma")

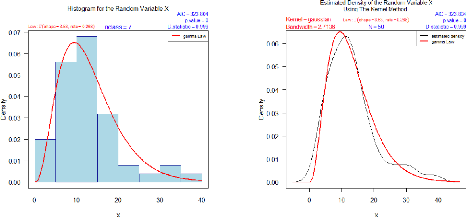
FIGURE 4.12 - Ajustement de la distribution de

1/'r^s=1

c par la méthode d'histogramme. FIGURE 4.13 - Ajustement de la distribution de

1/'r^s=1

c par la méthode du noyau.

Modèle M ó s>1(Vt)

Le processus de diffusion radial, qui décrit ce modèle est donné par l'équation différentielle stochastique suivante :

? ? ?

( ó2 ) 2 Rs-1 t -K dRt = dt + ód ^-Wt, R^st R0 = a

a > 0, t E [0,T] (4.32)

L'estimation de la densité de probabilité de la variable aléatoire ô(s>1)

c sera effectuée sur la base

de la simulation d'un flux de trajectoires. Les observations simulées de la variableô^(s>1)

c , seront

traitées statistiquement par deux méthodes, la méthode de l'histogramme et la méthode du noyau, pour estimer sa densité. Ce modèle est analytiquement difficile à résoudre.

Simulation la variable ô(s>1)

c

La fonction tho_M2 permettre de simulée un échantillonne de taille M = 50 de la variable

aléatoire ô(s>1)

c . Avec s = 2, K = 3 et ó = 1, le pas Ät = (T -t0)/N, et le c = v = 0.5.

R> tho_M2(N = 1000, M = + Sigma = 0.3) R> FPTT [1] 0.856 0.827 0.763 [12] 0.840 0.848 0.918 [23] 0.805 0.840 0.557 [34] 0.993 0.599 0.867 [45] 0.880 0.880 0.739

50, 0.795 0.952 0.821 0.790 0.602

t0 = 0, 0.710 0.662 0.833 0.935 0.794

T = 0.963 0.775 0.707 0.639 0.932

1, R0 0.948 0.894 0.661 0.868

= 2, v = 0.5, 0.620 0.895 0.769 0.599 0.597 0.751 0.973 0.579

K = 3, s = 0.788 0.831 0.676 0.971 0.694 0.732 0.832 0.904

2,

On fait l'ajustement de la variable Y = 1/ô^s=2

c par les lois : gamma, exponentiel, lognormale et

weibull. Le meilleur modèle est choisi par le critère AIC (minimum AIC).

R> Mod1 <- Ajdgamma(Y, starts = list(shape = 1, rate = 1), leve = 0.95)

$AIC

[1] 197.0462

R> Mod2 <- Ajdweibull(Y, starts = list(shape = 1, scale = 1), leve = 0.95) $AIC

[1] 203.6206

R> Mod3 <- Ajdexp(Y, starts = list(lambda = 1), leve = 0.95)

$AIC

[1] 294.9443

R> Mod4 <- Ajdlognorm(Y, starts = list(meanlog = 1, sdlog = 1), leve = 0.95) $AIC

[1] 199.8586

En remarque que la loi gamma ajuste mieux la distribution de la variable aléatoire Y = 1/ô^s=2

c ,

selon le critère AIC.