Memoire Online - La mécanique statistique des membranes biologiques confinées

Pour étudier les phénomènes dynamiques, la quantité d'intérêt est la fonction hauteur, h (r, t), qui dépend du vecteur-position r = (x, y) E R²et du temps, t. Cette dernière représente l'observation dans le temps du système, avant qu'il atteigne son état d'équilibre final. Nous rappelons que la fonction h (r, t) est solution de l'équation non-dissipative de Langevin (avec bruit) [28]

ah(r, t) at

= -Fan° ^[h]+ í(r, t) . (3.28)

ah(r, t)

Ici, n° est le Hamiltonien statique (divisé par kBT) et F > 0 est le coefficient cinétique. Ce dernier a les dimensions : [F] = L°T -1

de longueur et T_°est l'unité de temps. Ici, v (r, t) est une force aléatoire Gaussienne,

(v(r, t)v(r^', t^')) = 28e (r - r^') 8 (t - t^') . (3.29b)

La fonction de corrélation temporelle, dont la transformée de Fourier est le facteur de structure dynamique, est définie par la valeur moyenne suivante (par rapport au bruit),

G (r - r^', t - t^') = (h(r,t)h(r^',t^'))_í- (h(r,t))_í(h(r^',t^')) í , t > t^'.

L'équation dynamique (3.28) montre que la fonction hauteur h est une fonctionnelle du bruit v, et nous écrivons : h = h [v]. Au lieu de résoudre l'équation de Langevin pour h [v], puis moyenner, ensuite, sur la distribution du bruit, P [v], les fonctions de corrélation et de réponse peuvent être directement calculées à l'aide de la théorie du champ usuelle, d'action [28 - 31]

(O)_í= [dv] O [? [v]] P [v] =

DhD~hOe-A[h,h]

(3.32)

DhD~he-A[h,h] ,

où h (r, t) est un champ auxiliaire, couplé au champ externe h (r, t).

Les fonctions de corrélation et de réponse peuvent être calculées en remplaçant le Hamiltonien statique, H0, défini par la relation (3.13), par un nouveau, qui est : H0 [h, J] = H0 [h] - f d^erJh. En conséquence, pour une observable quelconque O, nous avons

ä (O)_J äJ (r,t)

J=0

~ ~

= h (r,t)O . (3.33)

La notation ~O~_J est la moyenne calculée avec l'action A h, h, J , associée à l'Ha-

miltonien H0 [h, J]. En raison de la structure de l'égalité (3.33), le champ conjugé h est appelé champ de réponse. Maintenant, si O = h, nous obtenons la réponse du champ de hauteur à la perturbation externe J,

R(r - r^',t - t^') = ä äJ (r,t'))J = Ch(r,t) h(r',t')> _ .(3.34)

La causalité implique que la fonction de réponse est nulle pour t < t^'. En fait, cette fonction peut être reliée à la fonction de corrélation temporelle, en utilisant le théorème de dissipation-fluctuation, selon lequel

h (r,t) h(r^',t^') = -è (t - t^')?t ~h(r,t)h(r^',t^')~_c . (3.35)

La formule ci-dessus montre que la fonction de corrélation temporelle, C (r - r^', t - t^') = (cp (r, t) cp (r^', t^'))_c, peut être déterminée par la connaissance de la fonction réponse. En particulier, nous trouvons que

L²1(t) = (h² (r, t))_c = -2 f (h, (r, t) h (r^', t^')) . (3.35a)

La limite t -* -oo donne la valeur normale L²₁ (-oo) = 0, car l'état initial correspond à une interface complètement plate.

Considérons, maintenant, une membrane à la température T, qui est initialement dans un état d'équilibre thermique où elle est plate. A un temps postérieur, t, la membrane possède une certaine rugosité, L1(t). Naturellement, cette dernière est une fonction du temps. Nous sommes intéressés par la façon dont il augmente au cours du temps. Nous précisons que les fluctuations thermiques provoquent une rugosité de la membrane, qui est caractérisée par l'apparition des bosses anisotropes. Par conséquent, un segment de taille linéaire L effectue des excursions de taille [32]

Une telle relation définit l'exposant de rugosité, (. Notons que L est de l'ordre de la longueur de corrélation parallèle , L11. De la relation (3.20), nous déduisons l'exposant ( et la valeur de l'amplitude B. Alors, nous avons ( = 1 et B ~ (kBT/ê)^1/2.

Afin de déterminer la croissance de la rugosité dans le temps, L1 (t), la clé est de considérer l'excès d'énergie libre (par unité d'aire) ?F, due au confinement (perte d'entropie). La formule (3.27) nous indique que ?F doit diminuer avec la séparation. Le résultat s'écrit [32]

En outre, une analyse attentive de l'équation de Langevin (3.28) montre que

?L? ??F

~ -

?t ?L?

= .Ð ~ .L-(1+2/æ~ . (3.38)

Nous soulignons que cette loi d'échelle est conforme aux prédictions de Monte Carlo [32, 33]. La solution de cette équation, de premier ordre, est [34]

où Lmax représente une certaine longueur d'onde, au-dessus de toutes les fluctuations

de forme, qui ne sont pas accessibles par la membrane confinée. L'interaction de

Premièrement, la rugosité augmente avec le temps (l'exposant è? étant défini positif). En plus, l'exposant è? est universel, indépendamment de la constante de rigidité de courbure ê.

Deuxièmement, notons que, dans l'égalité (3.39), nous avons ignoré une certaine amplitude, qui n'est pas universelle et se comportant comme ê-1/4. Cela signifie que la rugosité temporelle est significative, seulement pour ces biomembranes de petite

Quatrièmement, cette rugosité peut être interprétée comme la taille perpendiculaire des trous et vallées, au temps t.

Enfin, la rugosité augmente jusqu'à un temps final, ô. Ce dernier peut être interprété comme le temps au bout duquel le système atteint son état d'équilibre final. Le temps caractéristique se comporte comme

où nous avons ignoré une certaine amplitude dépendant de ê. Ici, LL ~ D est la rugosité finale. Explicitement, nous avons

Comme qu'il devrait être, le temps final augmente avec l'épaisseur du film D. d'une part, nous pouvons réécrire le comportement (3.39) comme suit

LL(t) LL(ô)

( t)è?

= .

(3.43)

Cette égalité signifie que le rapport de rugosité, en fonction du temps réduit, t/ô, est universel.

Maintenant, pour calculer la force de Casimir dynamique, nous partons d'une formule analogue à (3.24), c'est-à-dire

fj(t) kBT

ri(t) kBT

= -

Ce qui est très semblable à la relation statique (3.25), mais avec une rugosité de membrane dépendant du temps , L1 (t). La combinaison des formules (3.43) et (3.46) mène à l'expression désirée de la force de Casimir (par unité d'aire), en fonction du temps,

où ri(ô) est la force de Casimir statique finale, définie par la relation (3.25). L'exposant de force, èf, est tel que

Alors, la force induite se développe dans le temps comme t^1/2, jusqu'à ce qu'elle atteigne sa valeur finale, ri (ô). Au temps ô, l'amplitude de la force diminue comme ê-3/2. En outre, notons que l'égalité ci-dessus signifie que le rapport de force, en fonction du temps réduit, est universel.

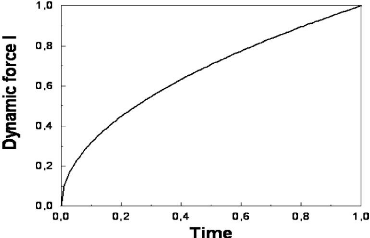
Dans la Fig. 3.2, nous reportons la force de Casimir dynamique réduite, ri (t) / ri (ô), en fonction du temps renormalisé t/ô.

où (ôh) est la force de Casimir statique, relation (3.25). Le nouvel exposant de

FIG. 4-2 -- La force de Casimir dynamique réduite, (t) / (ô), en fonction du temps renormalisé t/ô.

Considérons cette fois-ci une membrane, qui en présence d'interactions hydrodynamiques. Dans ce cas, la rugosité se développe dans le temps comme [35]

~L?(t) ~ t^~e? ,

~è? =î

1 + 2î

=(3.49) 3 .

Donc, l'augmentation de la rugosité avec le temps est relativement plus rapide que celle où la membrane est en absence d'interactions hydrodynamiques. Dans cette situation, la force de Casimir dynamique est telle que

h (t)

(ôh)

~ t ~

= ô

ê_f

(3.50)

FIG. 4-3 -- La force dynamique réduite (avec des interactions hydrodynamiques), Hh (t) /H (Th), en fonction du temps renormalisé t/Th.

2æ

èf = 2^~è? = 1 + 2æ

= 3
· (3.51)

Ici, Th ~ D³est la nouvelle échelle de temps, au bout duquel la membrane confinée atteint son état d'équilibre final. Par conséquent, la force de Casimir dynamique croit avec du temps comme t²/³, donc plus rapidement que celle en l'absence d'interactions hydrodynamiques, qui croit plutôt comme t¹/².

Nous illustrons, dans la Fig. 3.3, la variation de la force dynamique réduite (avec des interactions hydrodynamiques), Hh (t) /H (Th), en fonction du temps renormali-sée t/Th.

Après, nous avons abordé le calcul de la force de Casimir statique, fJ. A l'équi-

La mécanique statistique des membranes biologiques confinées

4.4 Force de Casimir dynamique.