6.3. Théorie des graphes
Dans la structure des réseaux, une configuration est un
ensemble de graphes. On définit un graphe comme une construction
topologique d'un ensemble de points ou sommets d'un système industriel
[2,], la conduite reliant ces points exemple réseau électrique
(noeud générateur, noeud de charge) constituent une
structure de branches entre eux. Dans la modélisation, on désigne
un graphe de 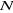 noeuds et de noeuds et de 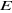 branches par : branches par :
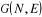
On dit qu'une construction topologique est complet si le
graphe dans lequel l'ensemble des couples de noeuds est relié par une
conduite c'est à dire (branches).
6.3.1. Exemple
illustratif
Considérons la configuration complète suivante,
constituée par quatre (4) noeuds à six (6) branches.
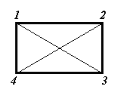
Fig. (6-1) : Réseau à quatre noeuds
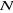 =4 01, 02, 03, et 04. =4 01, 02, 03, et 04.
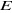 =6 ( 12 ), ( 23 ), ( 34 ), ( 41 ), ( 24 ), ( 13 ). =6 ( 12 ), ( 23 ), ( 34 ), ( 41 ), ( 24 ), ( 13 ).
Cela nous conduit à modéliser la topologie
complète par :
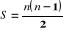 (6-23) (6-23)
Un arbre c'est le graphe d'une topologie sans boucle
(cycle). Par les mêmes noeuds on peut déterminer
différents arbres.
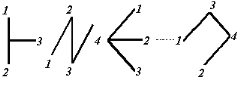
Fig. (6-2) : Les arbres possibles
Un arbre de 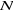 noeuds à : noeuds à :
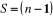 (6-24) (6-24)
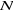 = 4 donc S = 4-1 = 3 branches. = 4 donc S = 4-1 = 3 branches.
Si on ajoute un arc à un arbre, on crée une
branche supplémentaire, on aura un graphe avec une boucle.
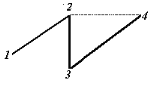
Fig. (6-3) : Arbre avec boucle
Si ont supprime un arc de l'arbre, nous obtenons des
schémas illogiques.
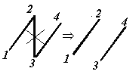
Fig. (6-4) : Schéma incomplet
D'après le théorème de
Cayley, avec n sommets, le
nombre d'arbres qu'on peut former est déterminé par :
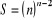 (6-26) (6-26)
Comme exemple une topologie formée par 04 sommets n
= 04, nous avons un graphe complet :
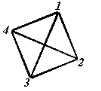
Fig. (6-5) : Graphe complet
Mais avec c = 4(4-2) = 16
différents arbres.
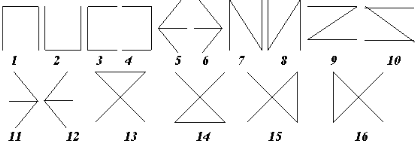
Fig. (6-6) : Différents arbres d'un réseau
à quatre noeuds
| 


