2.1.2.2. Fluctuations critiques et
ralentissement critique
Lorsque nous approchons le point critique, ils se
présentent des fluctuations plus grandes, observées sur nos
grandeurs habituelles, c'est le fait des phénomènes critiques.
Reprenons l'exemple de l'eau présenté au paragraphe sur les
transitions de phases ; au cours d'une transition critique, les
fluctuations spatiales de certaines grandeurs thermodynamiques possèdent
toutes les échelles de longueurs possibles. Ce phénomène
est relativement inhabituel pour le physicien qui généralement se
concentre sur une échelle de longueur donnée pour résoudre
un problème.
Ces fluctuations ralentissent la marche du processus Markovien
et par là induisent un ralentissement du processus. Il est dit critique
à ces températures environnent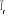 . Le temps de corrélation grandi dangereusement, nous le
retrouverons par les corrélations existant entre états. . Le temps de corrélation grandi dangereusement, nous le
retrouverons par les corrélations existant entre états.
2.1.2.3. Fonction d'auto
corrélation de l'aimantation
Dans une simulation, il est en général beaucoup
plus facile de calculer la fonction de corrélation telle définie
au 1er chapitre (équations 1.26 et 1.27 du §A.1.2)
dès lors que l'on se place à l'état d'équilibre.
Lorsqu'on opère des mesures d'aimantation ou d'énergie sur divers
systèmes de même dimension, l'on constate qu'ils arrivent presque
simultanément à la transition. Ce qui nous permet de penser qu'il
existe effectivement des corrélations qui s'établissent entre les
états du système. La fonction d'auto corrélation nous
permettra notamment de déterminer le temps de corrélation.
Considérons le modèle d'Ising avec lequel l'on détermine
l'aimantation m, nous avons présenté l'expression de la
susceptibilité (1.26) & (1.27) puis la fonction de
corrélation (1.33), ce qui nous permet en posant que m(t) est
l'aimantation instantanée au temps t, de décrire une fonction
d'auto corrélation de l'aimantation par l'équation (2.5)
et sous sa forme discrète, l'équation (2.6)
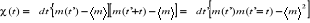 (2.5) (2.5)
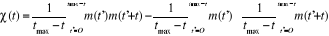 (2.6) (2.6)
La fonction d'auto corrélation donne la
corrélation entres deux instants distincts. Si nous intégrons
l'équation (2.5) précédente, 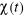 sera non nulle si en moyenne les fluctuations sont
corrélées et nulle dans le cas contraire. Globalement, l'on
obtient une échelle typique de mesure de la fonction d'auto
corrélation. Après un temps long, elle tendra vers une valeur
exponentielle définie par : sera non nulle si en moyenne les fluctuations sont
corrélées et nulle dans le cas contraire. Globalement, l'on
obtient une échelle typique de mesure de la fonction d'auto
corrélation. Après un temps long, elle tendra vers une valeur
exponentielle définie par : 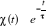 (2.7) (2.7)
On constate que le temps de corrélation noté
ô diminue de 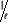 de sa valeur maximale à t = 0. de sa valeur maximale à t = 0.
Par ailleurs sur l'expression discrète (qu'on peut
compiler sur un ordinateur), lorsque t = tmax, la limite
supérieure devient petite et nous intégrerons donc sur un temps
vraiment court pour avoir le résultat escompté. Ceci nous informe
donc qu'à cause du hasard des fluctuations, l'erreur commise sur le
temps de corrélation devient grande. Il faudra donc simuler pendant un
temps grand pour réduire cet inconvénient.
| 


