3.3. Détermination du temps
de corrélation.
Une fois l'équilibre thermique atteint, nous avons
effectué la mesure des grandeurs physiques qui nous intéressent
en l'occurrence, l'énergie « E », l'aimantation
« M », la chaleur spécifique à volume
constant « C », la susceptibilité magnétique
du système « ÷ » ... . Mais combien de mesures
indépendantes (non corrélées) ces données
représentent ? Autrement dit, quel est le temps de
corrélation ? Pour répondre à cette question, nous
devons déterminer le temps de corrélation à chaque
température. Pour ce faire, nous calculons la fonction d'auto
corrélation de l'aimantation à chaque température
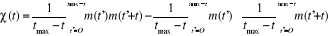
Nous représentons ci-dessous en figure 3.5 un exemple
de cette fonction à T= 2.2K.
Afin de déterminer le comportement en
température du temps de corrélation, nous avons mesuré
l'aimantation du système pour un temps d'observation en MCS/Site allant
de 2000 exceptées les températures T=2.2K et T=2.3K pour
lesquelles t variait de 0 à 4000 MCS/Site. Nous avons
déterminé ensuite à chaque température le temps de
corrélation ô qui est le temps au bout duquel la fonction d'auto
corrélation diminue de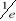 de sa valeur maximale à t = 0.
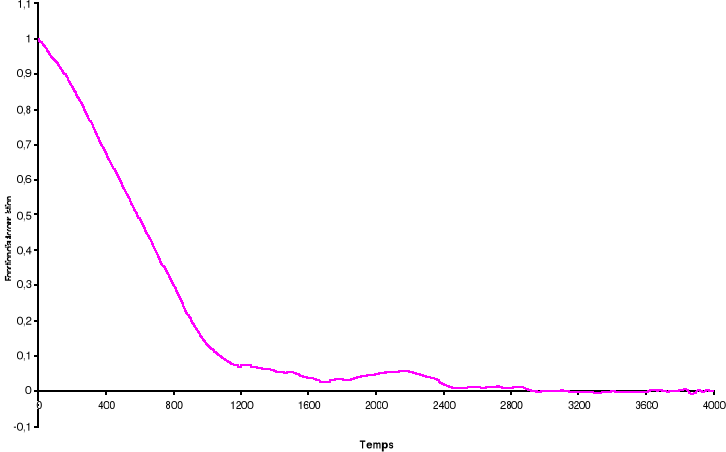
Figure
3.5 : Fonction d'auto corrélation de
l'aimantation pour le modèle d'Ising à 2D sur un système
de 100x100 spins à la température T=2.2K par Métropolis.
Le temps de corrélation est de ô = 725 MCS/Site
Pour T=2.2°K par exemple, nous avons obtenu un temps de
corrélation de ô = 725MCS/Site. Nous avons
représenté sur la figure 3.6 ci-dessous, les résultats
obtenus pour une gamme de températures allant de 0.2K à 5K et par
pas de 0.1K. Nous observons sur la figure une divergence à T=2.3K. Ce
phénomène est appelé ralentissement critique. Ce qui
signifie que dans la zone critique le système prend
énormément de temps pour atteindre l'équilibre d'une part
et d'autre part pour passer d'une configuration stable vers une autre :
Figure
3.6 : Temps de corrélation pour 100x100 spins
du modèle d'Ising à 2D en fonction de la température
simulé avec l'algorithme de Métropolis.
NB. Le trait continu est juste un guide pour l'oeil
Nous remarquons également qu'en dehors de la zone
critique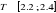 , le temps de corrélation est inférieur à 40
MCS/Site (ô?35), condition que nous utiliserons par la suite dans nos
simulations.
Disposant de toutes ces informations liées à la
bonne marche de nos processus de calcul, nous pouvons à présent
nous intéresser à la transition de phase et aux
phénomènes au voisinage de la transition.
| 
