3.4. Etude de la transition de
phase.
Afin de nous assurer que notre programme fonctionne bien, nous
l'avons au préalable testé sur un petit réseau de 5x5
spins (soit 25 spins ou 225 états possibles) dans la gamme de
températures allant de 0.2K à 5K. Dans ces conditions, toutes les
simulations à une température donnée ne prenaient que
quelques 2 à 3 secondes.
L'objectif étant de tester la validité de notre
programme, nous n'avons ni déterminé la configuration à
l'équilibre, ni le temps de corrélation entre 2 mesures
consécutives. Pour chaque température, nous avons simplement fait
tourné le programme pendant un temps de 20000 MCS/Site et
effectué les mesures à partir de t = 2000 MCS/Site et par
intervalle de Ät= 5 MCS/Site.
Les figures 3.7 et 3.8 ci-dessous montrent les
résultats normalisés à l'unité ( 1 ) (carrés
et cercles) de notre simulation et ceux (traits pleins) obtenus par un calcul
exact à l'aide de la fonction de partition
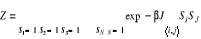
où 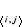 est la somme sur les premiers voisins. est la somme sur les premiers voisins.
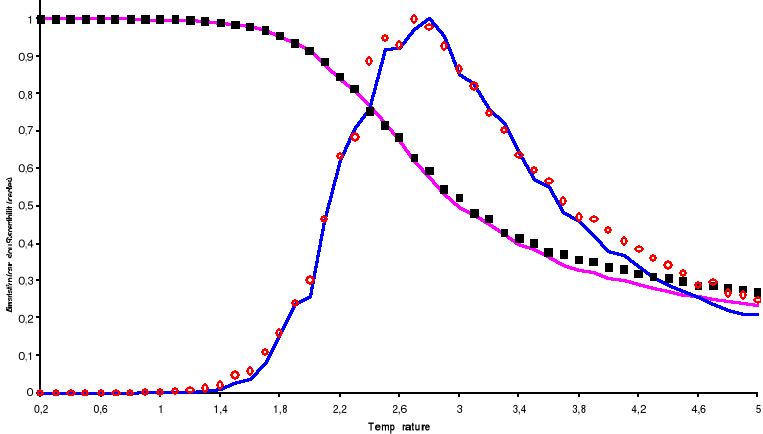
Figure
3.7 : Aimantation (carrés) et
susceptibilité magnétique (cercles) du système 5x5 spins
du modèle d'Ising à 2D en fonction de la température
simulé avec l'algorithme de Métropolis. Les points
(carrés et cercles) sont les résultats de la simulation et les
traits, le calcul exacte à l'aide de la fonction de partition.
Au vu de ces résultats, nous pouvons conclure sans
ambiguïté que notre programme fait bien son travail, et commencer
dès lors l'étude de la transition de phase Ferro ? Para.
3.4.1. Transition de phase
Ferro?Para.
Une transition de phase rappelons le, est un processus qui
fait passer le système d'une phase (de symétrie ou de
configuration donnée) vers une autre phase (de symétrie ou de
configuration différente de la phase de départ). Ce processus est
gouverné par une grandeur appelée paramètre d'ordre
noté ç. Ce paramètre d'ordre est non nul dans la
phase ordonnée et nul dans la phase désordonnée.
Pour les transitions de phase magnétique, le paramètre d'ordre
est l'aimantation du système noté â. A la transition, la
susceptibilité magnétique du système et la chaleur
spécifique à volume constant ont des comportements singuliers.
Elles divergent à la transition. Alors que l'aimantation passera
continûment d'une phase à une autre (transition du 2nd
ordre) ou bien passera directement d'une phase à une autre (transition
du 1er ordre).
Pour étudier cette transition, nous avons
considéré un système de 100 x 100 spins à J = 1 et
nous avons effectué nos mesures dans la gamme de température
allant de 0,2K à 5K et par pas de 0,1. Pour chaque température,
le système est d'abord amené à l'équilibre et les
mesures sont effectuées par intervalle de temps Ät = ô
déterminé précédemment.
Afin d'éviter des mesures dans les zones de saturation
où les variations des grandeurs physiques sont faibles et conduisent
à des résultats peu précis, Newman et Bakerna [2]
proposent de commencer les mesures dès que 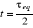 où où 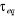 est le temps
d'équilibre en MCS/Site. est le temps
d'équilibre en MCS/Site.
Nous avons considéré pour nos simulations deux
configurations initiales de notre système de spins :
o Une configuration dans laquelle tous les spins sont
alignés.
(C'est à dire à la température T =
0K) : Transitions Ferro?Para,
o Une configuration dans laquelle tous les spins sont
aléatoirement orientés Up ou Down.
(C'est à dire la température est infinie) :
Transition Para?Ferro.
A chaque température et pour toute les mesures, nous
avons alors pris le temps d'équilibre 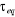 = 1000 MCS/Site et le temps de corrélation ô = 10 MCS/Site,
avec un temps d'observation global de 2000 MCS/Site. C'est à dire = 1000 MCS/Site et le temps de corrélation ô = 10 MCS/Site,
avec un temps d'observation global de 2000 MCS/Site. C'est à dire 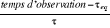 =100 mesures indépendantes. =100 mesures indépendantes.
Les résultats normalisés à l'unité
( 1 ) sont représentés sur la figure 3.8 pour l'aimantation
moyenne par spin du système, sur la figure 3.9 pour la chaleur
spécifique moyenne à volume constant et sur la figure 3.10 pour
la susceptibilité magnétique moyenne du système.
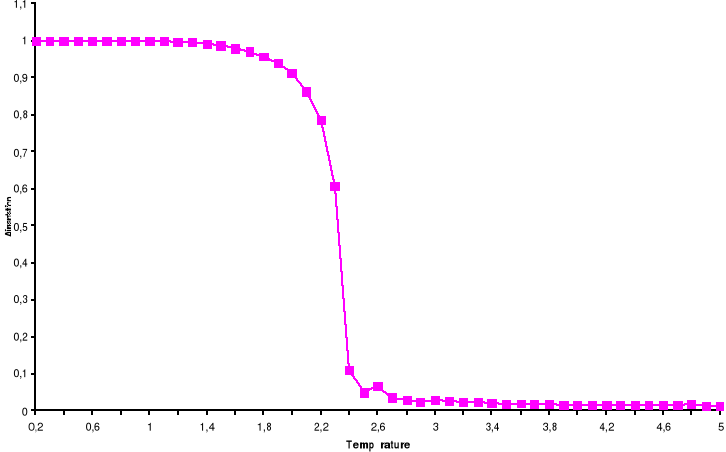
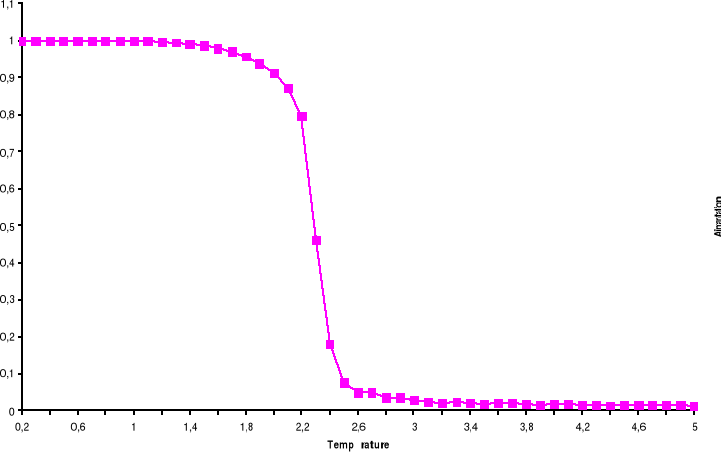
Figure
3.8 : Aimantation moyenne par spin du système
100x100 spins du modèle d'Ising à 2D en fonction de la
température, simulé avec l'algorithme de Métropolis. Le
tracé représente la Transition Ferro ? Para. Le tracé
représente la Transition Para? Ferro
Le trait continu n'est juste qu'un guide pour l'oeil.
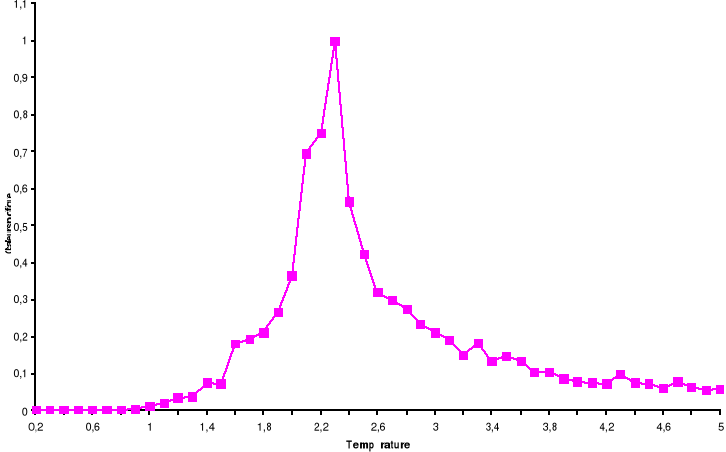
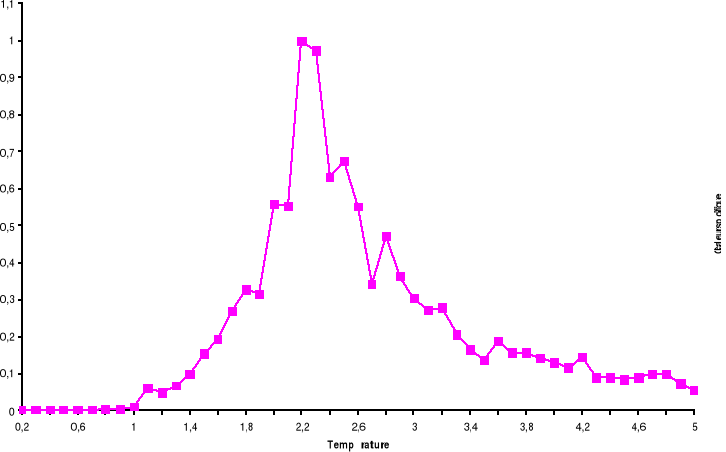
Figure
3.9 : Chaleur spécifique moyenne à
volume constant par spin du système 100x100 spins du modèle
d'Ising à 2D en fonction de la température, simulé avec
l'algorithme de Métropolis. Le tracé représente la
Transition Ferro ? Para. Le tracé représente la Transition Para?
Ferro
Le trait continu n'est juste qu'un guide pour l'oeil.
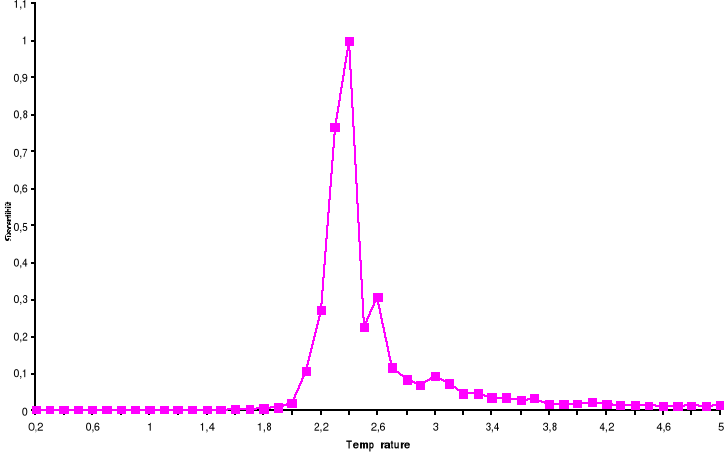
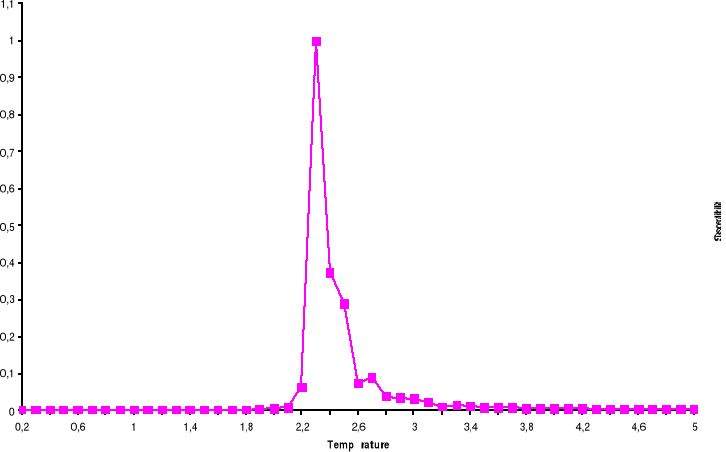
Figure
3.10 : Susceptibilité magnétique
moyenne par spin du système 100x100 spins du modèle d'Ising
à 2D en fonction de la température, simulé avec
l'algorithme de Métropolis. Le tracé représente la
Transition Ferro ? Para. Le tracé représente la Transition Para?
Ferro
Le trait continu n'est juste qu'un guide pour l'oeil.
Nous faisons le constat direct que les résultats sont
meilleurs pour la transition Para ? Ferro. Par ailleurs, aucune
hystérésis thermique n'a été observée durant
les deux cycles, et la transition de phase se produit à 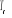 =2.3K appelée température critique -la chaleur
spécifique et la susceptibilité magnétique divergent
toutes les deux à =2.3K appelée température critique -la chaleur
spécifique et la susceptibilité magnétique divergent
toutes les deux à 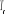 =2.3K, caractéristique d'un changement de phase- très
proche de la valeur théorique exacte =2.3K, caractéristique d'un changement de phase- très
proche de la valeur théorique exacte 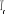 =2.2692K déterminée par Onsager's. De même, les
résultats de la figure 3.8 montrent clairement qu'au dessus de la zone
critique, l'aimantation moyenne par spin devient petite et tend vers
zéro (0) aux grandes températures alors quelle tend vers un (1)
en dessous de cette zone, ce qui est caractéristique du paramètre
d'ordre d'une transition de phase. =2.2692K déterminée par Onsager's. De même, les
résultats de la figure 3.8 montrent clairement qu'au dessus de la zone
critique, l'aimantation moyenne par spin devient petite et tend vers
zéro (0) aux grandes températures alors quelle tend vers un (1)
en dessous de cette zone, ce qui est caractéristique du paramètre
d'ordre d'une transition de phase.
Ces résultats permettent également de conclure
en l'occurrence pour ce qui est de la chaleur spécifique et de la
susceptibilité que les fluctuations critiques ne sont pas
maîtrisées, problème lié à l'algorithme de
Métropolis et résolu par l'algorithme de Wolff.
En effet, lorsqu'on se rapproche de la transition de phase
(à partir des hautes températures), les spins initialement
désordonnés et non corrélés auront tendance
(grâce aux interactions entre eux) à se regrouper en blocs de
même orientation, formant ainsi des clusters dont la taille î
croît lorsque T? et diverge même à la transition. et diverge même à la transition.
| 


