2.2.1.4.Modélisation des spectres
Une manière courante d'analyser des spectres de
diffusion de neutrons est de postuler que les différents types de
mouvements : vibrationnels, rotationnels et translationnels sont
découplés. Ceci n'a de validité que si les dynamiques
respectives présentent au moins un ou plusieurs ordre(s) de grandeur
~~
d'écart. Dans le cadre de cette approximation, la
fonction de diffusion Sinc (Q, E) s'exprime alors
comme le produit de convolution des facteurs de structure
correspondant aux différents types de mouvements :
~~ ~~ ~~ ~~
Sinc(Q,E) SV(Q,E)? SR(Q,E)?
ST(Q,E) (Eq. 2)
~~ ~~ ~~
où SV(Q,E) ,SR(Q,E) et ST(Q,E)
sont les fonctions de diffusion vibrationnelle, rotationnelle et
translationnelle respectivement.
Dans la région quasi-élastique qui nous
intéresse (c'est-à-dire pour des énergies E < 1meV),
la
fonction de diffusion vibrationnelle se limite à un facteur
Debye-Waller (DW)*. Le DW est

*Le facteur Debye-Waller (DW) s'exprime en fonction
du déplacement quadratique moyen u2 et du transfert
u2 Q2 /3
de moment Q : DW = e .
indépendant de l'énergie et prend en compte la
diminution de l'intensité quasi-élastique en fonction de Q, une
diminution qui est liée à des mouvements rapides se produisant en
dehors de la région quasiélastique.88 La fonction de
diffusion peut alors être exprimée uniquement en fonction des
facteurs de structure dynamique de rotation et de translation dans le domaine
quasi-élastique considéré:
2 2
~~ u Q
. ~~ ~~
S inc
(Eq. 3)
( , ) exp ( , ) ( , ) ( )
Q E S Q E S Q E R E
. R T
? ?
3 [ ?
La fonction de diffusion totale n'est désormais
composée que de deux termes correspondant à des mouvements de
type diffusifs. Deux modèles sont couramment utilisés pour
décrire ces type de mouvements: (i) le modèle dit de diffusion
par sauts, et (ii) le modèle de l'exponentielle étirée.
Dans notre cas, le modèle de l'exponentielle étirée ne
nous a pas permis d'obtenir un ajustement satisfaisant et par conséquent
n'a pas donné de résultats probants. C'est pour cette raison que
nous ne décrirons ici que le modèle de diffusion par sauts. Ce
modèle comporte deux composantes, une gaussienne, qui prend en compte la
diffusion élastique, et une composante Lorentzienne, qui prend en compte
tous les autres types de mouvements présents dans le système.
La deuxième loi de Fick, également baptisée
équation de diffusion, gouverne les mouvements de diffusion continue:
2 ( , )
( , ) C r t
0
D C r t V(Eq. 4)
0t
dans laquelle C(r,t)est la probabilité pour une particule
d'être à la position r à l'instant t et D est le
coefficient de diffusion de cette particule.
Sachant que les conditions aux limites sont C(r, 0)N(r) (N est
le nombre total de particules) et C(r, t - oc)0, la solution de cette
équation est une gaussienne*. Sa double transformée de
Fourier dans l'espace et le temps permet d'accéder au facteur de
structure dynamique incohérent:
1 ( )
[' Q
S Q E Q E
( , ) ( , )
.J7(Eq.5)
inc ( )
Q E
2 2
['
Le spectre de neutrons correspondant est une Lorentzienne avec
une demi-largeur à mi-hauteur
['(Q) /2. La théorie
d'Einstein89 sur le mouvement Brownien permet de faire le lien
entre
N
* L'équation de la fonction gaussienne solution de
l'équation est: C r t r Dt
2
( , ) 3/2 exp 4
(4 )
Dt
l'élargissement de la fonction de diffusion et le
coefficient de diffusion. Le modèle de diffusion continue prédit
pour ['(Q) la forme suivante:
2 ? DQ 2
[' ( Q )(Eq. 6)
où D est le coefficient de diffusion.
Cependant, ce modèle n'est valide que pour des forces
d'interaction intermoléculaires relativement faibles, et dans le cas
d'interactions plus fortes, comme dans les liquides structurés par
exemple, il est remplacé par le modèle de diffusion par sauts. Ce
modèle décrit des systèmes dans lesquels les
molécules présentent des mouvements oscillants localisés
présentant occasionnellement des mouvements de translation, durant
lesquels les molécules peuvent diffuser sur des distances
supérieures à leur amplitude de vibration. Le modèle de
diffusion par sauts définit deux nouveaux temps caractéristiques:
(i) le temps de saut r J durant lequel la particule
diffuse, et (ii) le temps de
résidence r0 durant lequel la
particule oscille sans translation.90 Dans la partie
quasi-élastique, ce
modèle donne lieu à des lois de diffusion qui
dévient du régime continu pour de grandes valeurs de Q. La
largeur à mi-hauteur s'exprime alors de la manière suivante:
2
? **
DQ 2
[' ( )
Q (Eq. 7)
1 J
Q Dr
2
Le temps de saut r J et la longueur de saut
caractéristique l0 sont reliés au coefficient de
diffusion D par la relation:

La fonction de diffusion translationnelle ST (Q, E)
utilisée ici est donc extraite de ces travaux classiques et de travaux
plus récents sur l'eau91,92 dans lesquels ST (Q,
E) est modélisée par la fonction Lorentzienne.t?(Wt,E)
suivante:
1 2
W t
S Q E W E
( , ) ( , )
.t?(Eq. 9) T t ( 2)
W E

2 2
t
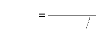
2
2
W t
?DQ
avec
1 6
l Q
2 2
** Notons que pour des petites valeurs de Q, la loi de diffusion
par saut se réduit au modèle continu. (Eq. 6)
La diffusion rotationnelle, quant à elle, a
été modélisée à l'aide des premiers termes
du développement limité développé par
Sears93 pour la diffusion rotationelle d'une molécule
libre:
|
8
S Q E A
R i
( , ) ( ) ( ) ( , )
E A Q W E
~
0 i r
i1
|
(Eq. 10)
|
? i i
( 1)
2
avec A i ( Q ) (2 i 1) j i
(amQ), où am est le rayon moléculaire
effectif, W, et ôR est le
ri 3 ô R
temps de relaxation rotationnel.
Dans la gamme de Q utilisée ici, c'est-à-dire pour
Q < 2Å-1, le coefficient amQ présente
une
décroissance rapide avec i, et au-delà de i=3,
les termes deviennent négligeables. Ici, seuls les deux premiers termes
de ce développement, qui contribuent de manière significative,
ont été considérés dans cette étude.
Dans l'approximation d'une diffusion cohérente
négligeable devant le signal incohérent, et à partir des
équations précédentes, nous pouvons exprimer
littéralement le facteur de structure dynamique total
incohérent:

u Q
S
inc total
2 2 ? 8 ?
(Eq. 11)
( , ) exp ( , ) ( ) ( ) ( , ) ( )
Q E W E A
? ?
~ E A Q W E R E
~ ? ?
t 0 i r Ò
3 ? ?
i
[ i 1 ?
dans lequel R(E) est la résolution de l'instrument,
obtenue en mesurant un spectre élastique de l'échantillon
complètement gelé ou un échantillon de vanadium.
A partir de l'ajustement, pour chaque valeur de transfert de
moment Q, du facteur de structure dynamique total incohérent (Eq. 11) au
signal quasi-élastique incohérent expérimental, il est
possible d'extraire les paramètres suivants:
1. la largeur à mi-hauteur W t
2
2 ? DQ
de la Lorentzienne «étroite» qui décrit
les

1 6
l Q
2 2
mouvements de translations des molécules,
2. la largeur à mi-hauteurWr de la Lorentzienne
«large » qui décrit les mouvements de rotation des
molécules.
| 


