2.2.1.5. Résultats
2.2.1.5.1. DCS
inc
La fonction de diffusion théorique S Q E
( , ) a été ajustée aux données
expérimentales pour
total
chaque valeur de transfert de moment Q. Le meilleur ajustement
a été obtenu en combinant une fonction gaussienne étroite
(fonction delta), deux fonctions Lorentziennes (une large et une plus
étroite) et une ligne de base à pente non nulle afin d'autoriser
une légère déviation du signal de diffusion
inélastique (Figure 15). L'expression complète est donnée
ci-dessous:
Sinc
(Q,E)[(E)c1(Q).L(W1,E)c2(Q).L( W 2
,E)a?bE]R(E) (Eq. 12)
où R(E) est la résolution instrumentale et L(Wi,E)
une fonction Lorentzienne avec une largeur à mi- hauteur Wi, et(E) une
fonction delta.
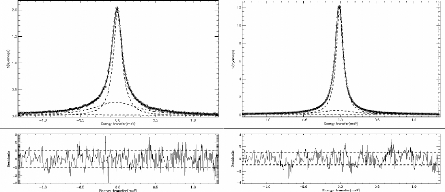
Figure 15: Deux exemples d'ajustements des données du
DCS composés de deux fonctions Lorentziennes et d'une ligne de base. Il
s'agit ici de l'eau (H2O) à gauche et du d-glc+H2O, 1:55 à droite
à 280K et à Q = 0,97Î1. Les résidus sont
présentés en dessous de chaque courbe.
Deux fonctions Lorentziennes sont ici nécessaires dans
l'ajustement: (i) une large pour les mouvements de rotation de la
molécule, et (ii) une que l'on qualifiera d'étroite pour les
mouvements d'ensemble des molécules.
Les expressions théoriques de W t (Eq. 9 et
10) montrent une dépendance en Q2 de la largeur à mi-
hauteur pour les deux types de mouvements diffusifs. Le tracé de ces
largeurs à mi-hauteur W1 et W2 en fonction de Q2 est
présenté dans la figure 16 pour les trois échantillons
dont le solvant est l'eau (H2O, d-glc+H2O, 1/20 et d-glc+H2O, 1/55) ainsi que
pour l'échantillon contenant de l'eau lourde uniquement (D2O).
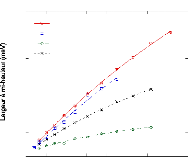
Lorentzienne "étroite" L1(W~~E)
(a)
H2O
T = 280 K
0,5
D2
O
0,4
d~glc+H2O, 1/20
d-glc+H2O, 1/55
0,3
0,2
0,1
0
0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å2) (b) Lorentzienne "large"
L2(W~~E)
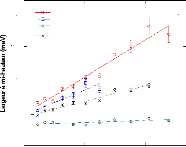
T = 280 K
H2O D2O d-glc+H2O, 1/20
d-glc+H2O, 1/55
0
2
1,5
1
0,5
0 0,5 1 1,5 2 2,5 3 3,5 4
Q2 (Å2)
Figure 16: Largeur à mi-hauteur de la Lorentzienne
étroite W1 (a) et de la Lorentzienne large W2 (b) ajustées aux
données de l'eau et des solutions de glucose. Les courbes
représentent les ajustements effectués à partir des
équations 9 et 10.
Le tracé de W1 en fonction de Q2 montre une
première région linéaire qui tend à s'aplanir pour
atteindre une valeur constante théoriquement égale à 1 /
ô0. Cette dépendance non-linéaire en
Q2 de W1
renforce l'utilisation du modèle de diffusion par
sauts. Nous remarquons que le plateau n'est atteint que pour
l'échantillon le plus concentré en sucre en raison de la gamme de
Q sondée ici. Le tracé de W2 en fonction de Q2 montre
une dépendance linéaire à pente non nulle.
Théoriquement, W2 est indépendante de Q2 dans le cas
de mouvements parfaitement découplés. Cependant, pour pouvoir
découpler complètement les deux types de mouvements, il aurait
fallu pouvoir utiliser plus de deux fonctions Lorentziennes convoluées
avec la résolution durant l'ajustement, ce qui n'a pas été
possible dans notre cas. Nous estimerons donc W2 à sa valeur pour Q =
0.
La dépendance en Q2 des W n a
été ajustée par la méthode des moindres
carrés à l'aide des expressions suivantes:
Q 2
1
W(Eq. 13)
1 1 2
1 ã 1 Q
2 Q 2
W 2 (Eq. 14)
2
L'expression de l'équation 13 a bien évidemment
été choisie en rapport avec l'expression théorique de W
t déterminée précédemment. En revanche,
celle de l'équation 14 a été choisie de manière
purement empirique. Les ajustements sont présentés sur la figure
16 sous forme de lignes continues et les valeurs des paramètreset
1 1 ã 1 sont regroupées dans le tableau 6. Nous
pouvons remarquer
2 2
le très bon accord qui existe entre les courbes
expérimentales et théoriques, témoignant de la
validité du modèle utilisé.

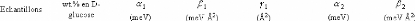

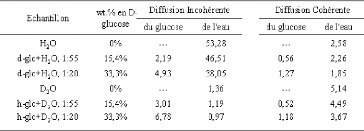
Tableau 6: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite W1 et pour la Lorentzienne large W2 à partir
des mesures réalisées sur le DCS à 280K.
Les valeurs des paramètres pour les échantillons
h-glc+D2O, 1:55 et h-glc+D2O, 1:20 doivent être manipulées avec
précaution. Le traitement direct de ces échantillons n'a pas
permis de les ajuster de manière complètement satisfaisante. Il
nous a fallu en effet soustraire le signal du solvant (D2O) afin de n'obtenir
plus que celui du sucre. Ce traitement supplémentaire ne peut être
considéré qu'approximatif en raison de la différence de
dynamique moléculaire existante dans un solvant pur et dans un solvant
contenant un soluté. Malgré cette soustraction,
l'échantillon h-glc+D2O, 1:20 ne nous a pas permis d'obtenir de
résultats valides. Cette difficulté de traitement a
vraisemblablement deux origines:
(i) les contributions relatives de la diffusion cohérente
et incohérente (Tableau 7) présentent un faible écart
relatif qui invalident l'approximation d'une diffusion cohérente
négligeable. Ce postulat inc
n'étant plus vérifié, notre expression
théorique de S Q E
( , ) n'est donc plus utilisable.
total
(ii) La diffusion incohérente du solvant et celle du
sucre s'équilibrent dans ces mélanges, rendant difficile la
séparation des signaux, et ce, malgré les deutérations
sélectives effectuées. Ainsi, au lieu de ne regarder que la
dynamique du D-glucose comme initialement prévu, c'est la dynamique
globale du mélange qui est sondée. (Tableau 7)
Tableau 7: Contributions relatives de la diffusion
cohérente et incohérente émanant du D-glucose et de l'eau
lourde ou légère.
Pour les échantillons préparés avec de
l'eau légère, l'approximation d'une diffusion cohérente
négligeable reste valable en raison du fort écart relatif
existant entre le signal cohérent et incohérent. De plus, les
contributions relatives de l'incohérent du sucre et de l'eau sont
suffisamment différentes pour permettre uniquement l'extraction du
signal provenant du sucre.
En rapprochant l'équation 9 de l'équation 13,
nous pouvons en déduire l'expression des paramètres
et ã1 :
1 1
0 (Eq. 15)
1
2 ? D (Eq. 16)
1
2
l
ã (Eq. 17)
1 6
De la même manière, en identifiant l'équation
10 à l'équation 14, il est possible de déterminer
l'expression analytique de2:
2

2
3 R
ô
(Eq. 18)
Les paramètresnous
1 1 ã 1 et permettent donc d'accéder aux
constantes physiques qui nous
2
intéressent, c-à-d le coefficient de diffusion D,
le temps de relaxation rotationel ôR ainsi que la
longueur de saut effective l. Les valeurs de ces constantes sont
répertoriées dans le tableau 8 suivant.
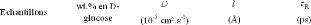

Tableau 8: Constantes physiques calculées à partir
des ajustements de W1 et W2 en fonction de Q.
2.2.1.5.2. HFBS
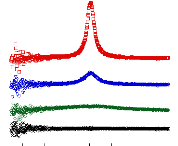
La figure 17 présente les fonctions de structure
dynamique S(Q, E) des échantillons H2O, D2O,
h-glc+D2O, 1:20 et h-glc+D2O, 1:55. Nous remarquons une nette
influence de l'effet de la concentration sur le profil de diffusion. Ainsi,
lorsque la concentration en D-glucose s'accroît, l'intensité du
pic augmente et sa largeur diminue, témoignant d'un ralentissement
général de la dynamique moléculaire du système.
h-glc+D20,
1:20
h-glc+D20, 1:55
H 2
D 2
o
o
-40 -30 -20 -10 0 10 20 30 40
E (geV)
Figure 17 : Spectres mesurés sur le HFBS pour les
échantillons D2O (croix), H20 (losanges), h-glc+D2O, 1:20
(cercles) et h-glc+D2O, 1:55 (carrés) à 280K pour
un vecteur de diffusion Q= 0,47Å-1.
Les mesures réalisées sur le DCS sur ces
mêmes échantillons nous ont donné des temps de relaxation
de l'ordre de la picoseconde et des constantes de diffusion proches de
10-5 cm2s-1 pour les molécules d'eau
à 280K. Dans la gamme des valeurs de Q utilisées ici, ces valeurs
correspondent à des largeurs à mi-hauteur maximales de l'ordre de
~ 200-1500 geV pour la partie rotationnelle et de ~ 300 geV pour la partie
translationnelle.* La part de l'eau dans la diffusion totale se
résume donc à un signal très large de faible
intensité qui ne contribue pas significativement au profil de diffusion,
comme en témoigne les profils de l'eau de la figure 17. Il en est de
même pour les mouvements de rotation des molécules de sucre qui
présentent des temps de relaxation de l'ordre de la picoseconde, et les
énergies mises en jeu (0,3 < E < 2meV) sont bien en dehors de la
fenêtre énergétique considérée ici. De ce
fait, l'ajustement n'a nécessité l'utilisation que d'une unique
fonction Lorentzienne. Les dynamiques respectives des six échantillons
et la sensibilité instrumentale n'ont permis d'exploiter que les
échantillons h-glc+D2O, 1:20 et h-glc+D2O, 1:55, les quatre autres
présentant des dynamiques beaucoup trop rapides. Néanmoins,
l'ajustement aux données expérimentales, composé dans ce
cas d'une fonction delta, d'une fonction Lorentzienne et d'une ligne de base
à pente non nulle, a donné des résultats concluants.
*La fenêtre énergétique du
spectromètre à rétrodiffusion HFBS ( #177;36?eV)
est nettement plus étroite que celle du spectromètre
à temps-de-vol DCS (~15meV).
Le tracé de la largeur à mi-hauteur de l'unique
fonction Lorentzienne considérée en fonction de Q2 est
présenté sur la figure 18. Cette figure montre de manière
non équivoque l'effet de la concentration en D-glucose sur la dynamique
moléculaire de ce même monosaccharide. Comme en témoignent
les barres d'erreur de l'échantillon contenant 15% de D-glucose, la
dynamique des molécules de sucre sort rapidement de la fenêtre
énergétique de l'instrument, confirmant nos hypothèses
précédentes pour les échantillons
hydrogénés.



|
|
|
|
T = 280 K
|
|
h-glc+D2O, 1:20
h-glc+D2O, 1:55
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
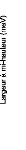
0,035
0,03
0,025
0,02
0,015
0,01
0,005
0

0 0,5 1 1,5 2
Q2 (A2)
Figure 18: Largeur à mi-hauteur, W1, de la fonction
Lorentzienne étroite ajustée aux mesures expérimentales
des solutions de glucose mesurées sur le HFBS.
Les valeurs des paramètres d'ajustement sont
présentées dans le tableau 9 et les constantes physiques qui en
découlent sont présentées dans le tableau 10.
Tableau 9: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite à partir des mesures réalisées
sur le HFBS à 280K.
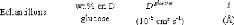

Tableau 10 : Constantes physiques calculées à
partir des ajustements de W en fonction de Q réalisés sur les
données du HFBS : Dglucose (Coefficient de diffusion) et l (distance de
saut effective).
| 


