2.2.2.3. Résultats
Les ajustements ont été réalisés
sur les trois échantillons (H2O, h-fruc+D2O, 1:24,5 et dfruc+H2O,
1:24,5) pour les trois températures considérées T = 280,
300 et 320 K. Le meilleur ajustement s'est avéré être
composé, comme dans le cas du D-glucose, d'une fonction delta, de deux
fonctions Lorentziennes (.L?~(W1,E) et.L?~(W2,E)) et
d'une ligne de base à pente non nulle. IRIS étant un
spectromètre à rétrodiffusion avec une
fenêtre énergétique assez étroite de #177; 400?eV,
toutes les fonctions de diffusion n'ont pas pu être ajustées avec
deux fonctions Lorentziennes, c'est entre autres le cas des échantillons
d'eau légère et de l'échantillon d-fruc+H2O, 1:24,5
à 320 K.

Les largeurs à mi-hauteur de la Lorentzienne «
étroite » W1 et de la Lorentzienne « large » W2 ont
été tracées en fonction de Q2 (Figures 22, 23
et 24). Comme pour son diastéréoisomère, W1
présente une dépendance quadratique en Q non-linéaire et
W2 une dépendance linéaire en Q2. Ces
dépendances ont été ajustées à l'aide des
expressions 13 et 14. Tous les paramètres d'ajustement sont
présentés dans le tableau 14.
Tableau 14 : Valeurs des différents paramètres
d'ajustements obtenus pour la Lorentzienne
étroite2~(W1,E) et pour la Lorentzienne large
2,(W2,E) à 280K.
2.2.2.4. Discussion
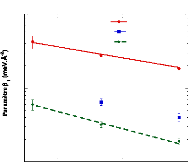
Les valeurs du paramètre de diffusion
translationnelle 1 et du paramètre de diffusion
rotationnelle a2 tracées dans la figure 21 en fonction de
1000/T(K) dévoilent une dépendance en température qui suit
une loi de type Arrhénienne k = A
·
e-Ea RT .
(a)
1
H 2
o
d-fruc+H20, 1:24,5
h-fruc+D20,
1:24,5
0,1
0,01
|
0,2
0,1 0,09 0,08
0,07
0,06
|
3,1 3,2 3,3 3,4 3,5 3,6
1000/1"(K) (b)
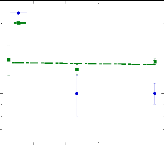
d-fruc+H20, 1:24,5
h-fruc+D20,
1:24,5
3,1 3,2 3,3 3,4 3,5 3,6
1000/1"(K)
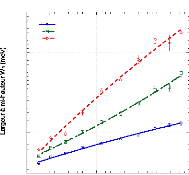
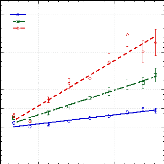
Figure 21 : Valeurs de fi1 (a)
et de a2 (b) pour les échantillons H2O,
h-fruc+D2O, 1:24,5 et d-fruc+H2O, 1:24,5 en fonction de 1000/T(K). Les lignes
représentent les ajustements de la loi d'Arrhenius aux
données.
Les énergies d'activation Ea correspondant
aux deux types de mouvements tirées des ajustements de la loi
d'Arrhenius sont présentées et comparées aux
résultat disponibles dans la
littérature49,76,77,78,92. (Tableau 15)
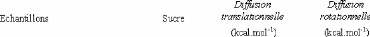


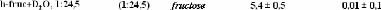
Tableau 15: Comparatif des énergies d'activation
Ea déterminées pour l'eau et les solutions de fructose
avec celles trouvées dans la littérature pour des solutions de
D-fructose et de D-glucose.
Ce qui ressort tout d'abord du tableau ci-dessus, c'est
l'accroissement de l'énergie d'activation de la diffusion
translationnelle de l'eau avec l'ajout du sucre : Ea passe ainsi de
(3,5 #177; 0,4) kcal mol-1 pour l'eau pure à (4,0 #177; 0,4)
kcal mol-1 pour une solution de fructose à 29 wt.%. Cet
excédent d'énergie témoigne du gain en stabilité de
la solution, une stabilité énergétique liée au
caractère stabilisateur de réseau du fructose. En d'autres
termes, le nombre de liaisons hydrogène (eau-eau, eau-sucre, sucre-
sucre) est supérieur au nombre de liaisons hydrogène
présentes dans l'eau pure (eau-eau), ce qui stabilise la solution et la
rend plus apte à résister aux contraintes extérieures.
Notons également l'évolution de Ea suivante:
Ea (h-fruc+D2O, 1:24,5) > Ea
(d-fruc+H2O, 1:24,5) > E a (H2O)
(Dfructose)
ou Ea > E a (Deau en
présence de fructose) > Ea (Deau)
Ces trois échantillons vont être traités
maintenant de manière séparée et nous reviendrons bien
sûr sur ces énergies d'activation que nous commenterons.

Dynamique de l'eau H20
La mesure de l'eau va jouer un double rôle: (i) d'abord
comme échantillon de référence afin de comparer les
valeurs des coefficients de diffusion déterminées dans ce travail
à des valeurs connues présentes dans la littérature, (ii)
mais également comme valeur à concentration nulle (0 wt.%) pour
l'étude de l'évolution de la dynamique du solvant en fonction de
la concentration en sucre.
1
0.8
H2O 280K
H2O 300K
H2O 320K
0.6
0.4
0.2
0
0 0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
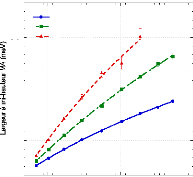
Figure 22: Variations de W1 en fonction de Q2 pour
l'eau légère à 280K (cercles), 300K (carrés) et
320K (triangles). Les lignes représentent les ajustements.
La figure 22 présente les variations de W1 en fonction
de Q2 pour les trois températures. Cette figure montre bien
le resserrement de la largeur à mi-hauteur de la Lorentzienne avec
l'abaissement en température, ce qui se traduit physiquement par un
ralentissement de la dynamique, qui est parfaitement corroboré par les
valeurs de DH2O. Un comportement somme toute logique en raison de la
diminution de l'agitation thermique, mais également de l'augmentation
progressive des interactions eau-eau en se rapprochant du point de
solidification situé à TS = 273 K.
Les différents ajustements présentés sur la
figure précédente ont permis de calculer les coefficients de
diffusion DH2O et les longueurs de sauts effectives l. (Tableau
16)
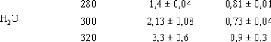
Tableau 16: Constantes physiques calculées à partir
des ajustements de W1 en fonction de Q.
Des travaux antérieurs sur l'eau donnent des valeurs
de DH2O = 1,34×10-5 cm2 s-1 à 280
K92, 2,67× 10-5 cm2 s-1
à 300 K79 et 3,43× 10-5 cm2 s-1
à 320 K92,*, des valeurs qui sont en très bon accord
avec nos résultats expérimentaux. Si l'on regarde maintenant
d'une manière plus qualitative ces résultats, nous remarquons que
DH2O augmente de manière significative entre 280 et 320 K,
passant de 1,4×10-5 à 3,3×10-5
cm2 s-1, c-à-d une augmentation d'un facteur ~
2,5. La dépendance en température de 1, autrement dit du
coefficient de diffusion DH2O, donne une énergie d'activation
moyenne pour la diffusion translationnelle de (3,5 #177; 0,4) kcal
mol-1, une valeur qui est très proche de 3,6 kcal
mol-1 déterminée dans l'étude classique de
l'eau réalisée par Teixeira et al.92 Notons
également que la longueur l n'évolue que très faiblement,
ne montrant pas de variation significative entre 280 et 320 K. Ainsi, la
longueur de saut reste quasi-constante dans la gamme en température
considérée, ce qui témoigne de
l'homogénéité de la structure du solvant avec la
température.
L'échantillon d-fruc+H20, 1:24,5 -- Dynamique du
solvant
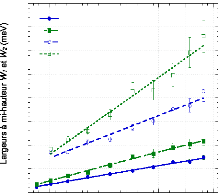
Les largeurs à mi-hauteur de la Lorentzienne «
étroite » W1 et de la Lorentzienne « large » W2 ont
été tracées en fonction de Q2 sur la figure
23.
0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Wi--T=280K Wi--T=300K W2 -- T = 280K W2 -- T = 300K
Figure 23: Largeurs à mi-hauteur W1 et W2 ajustées
aux mesures expérimentales de l'échantillon dfruc+H2O, 1:24,5
à 280 et 300K.
Cette figure montre de manière très claire la
différence énergétique qui existe entre les mouvements
de
rotation (partie supérieure) et les mouvements de translation
(partie inférieure). Comme dans le cas de
*Cette valeur est une valeur extrapolée
à partir des données de Teixeira et al.92
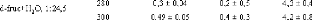
l'eau, W1 et W2 se rétrécissent avec
l'abaissement en température. Les paramètres a1 1, y,,
a2 et 2 tirés des ajustements de ces largeurs à
mi-hauteur, sont listés dans le tableau 14. Les constantes physiques qui
en découlent sont elles présentées dans le tableau
ci-dessous :
Tableau 17 : Constantes physiques calculées à
partir des ajustements de W1 : DH2O (Coefficient de
diffusion de l'eau) et l (distance de saut
effective).
Il faut remarquer tout d'abord que le coefficient de diffusion
de l'eau augmente de manière importante entre 280 et 300 K, passant de
DH2O = 0,3× 10-5 cm2 s-1 à 280 K
à DH 2O = 0,49×10-5 cm2
s-1 à 300K. La dynamique est ainsi divisée en moyenne
par un facteur ~ 4-5 par comparaison avec l'eau volumique. Cette diminution
reflète principalement l'effet du D-fructose sur la dynamique
moléculaire de l'eau, alors que le D-fructose ne contribue qu'à
hauteur de 12% dans la diffusion totale. Le coefficient f1 et donc
DH2O montrent une dépendance en température avec une
énergie d'activation Ea = (4,0 #177; 0,4) kcal
mol-1, valeur confirmée par Rampp et al. à partir de
la RMN à champs pulsés (Ea = 4,1 kcal
mol-1).78 A cela s'ajoute la faible augmentation de la
longueur de saut effective l qui passe de 0,2? à 0,4Å,
augmentation qui n'est pas réellement significative. A la
différence de la diffusion translationnelle, la diffusion rotationnelle
(ôR) ne varie pas avec la température,
observation corroborée par la faible
valeur de l'énergie d'activation correspondante
Ea = (0,3 #177; 0,2) kcal mol-1. Il faut toutefois
manipuler avec précaution les énergies d'activation
calculées dans le cas de l'échantillon d-fruc+H2O, 1:24,5 en
raison du faible nombre de points expérimentaux, en l'occurrence deux !
Si dans le cas de la diffusion translationnelle, le calcul de Ea
conduit à une valeur cohérente avec la littérature, il
n'en est pas de même pour la diffusion rotationnelle. En effet, les
valeurs connues de Ea pour l'eau pure et dans des solutions de
D-glucose sont très largement supérieures à cette valeur
(~ 6 fois), et aucune réelle justification ne peut expliquer un tel
écart si ce ne sont les incertitudes expérimentale et de
traitement.
L'échantillon h-fruc+D20, 1:24,5 -- Dynamique du
D-fructose
Les largeurs à mi-hauteur de la Lorentzienne «
étroite » W1 et de la Lorentzienne « large » W2 ont
été tracées en fonction de Q2 sur la figure
24.
Lorentzienne "étroite"21(W1,E)
(a)
T = 280K
T = 300K
T = 320K
0.15
0.1
0.05
0
0 0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
0.5 1 1.5 2 2.5 3 3.5
(b) Lorentzienne "large"22(W2,E)
0.6
0.5
0.3
0.2
0
T = 280K
T = 300K
T = 320K
Q2 (Å2)

Figure 24 : Largeurs à mi-hauteur étroite, W1 (a)
et large W1 (b) ajustées aux données de l'échantillon
hfruc+D2O, 1:24,5 à 280, 300et 320 K.
Il apparaît que comme pour l'eau, la température
induit un ralentissement de la dynamique moléculaire du D-fructose. Les
valeurs des coefficients de diffusion Dfructose nous montrent une diminution
d'un facteur ~ 3 pour une baisse en température de 40K. (Tableau 18) De
la même manière, la dynamique du sucre est en moyenne deux fois
plus lente que celle de l'eau pour une concentration de 29wt.% en
D-fructose.
Tableau 18 : Constantes physiques calculées à
partir des ajustements de W1 en fonction de la température T : Dfructose
(Coefficient de diffusion), l (distance de saut effective) et
DR (temps de relaxation orientationnel).
La dépendance en température de la dynamique
translationnelle conduit à une énergie
d'activation
Ea = (5,4 #177; 0,5) kcal mol-1, une
énergie légèrement supérieure à celle
déterminée dans le cas d'une
solution de D-glucose
(Ea = (3,8 #177; 0,4) kcal mol-1).76 La
longueur de saut l ainsi que le temps de
relaxation DR ne dépendent pas
particulièrement de la température. l varie entre 0,4Å et
0,6 Å, une
valeur légèrement supérieure à celle
de l'eau(<leau> = 0,3 Å). Cette conservation de l avec
la température reflète une certaine conservation de la
structuration de la solution avec la température.
La viscosité et la dynamique étant
étroitement liées, il est intéressant de comparer leur
évolution en fonction de la température. Rampp et
al.78 ont étudié la viscosité dynamique d'une
solution aqueuse de D-fructose (33 wt.%) et ont montré que la
viscosité diminuait d'un facteur ~ 2,5 entre 280 et 300 K passant de
17,2 à 6,77 Pa.s. Pour la même gamme de température, nous
avons observé une accélération de la dynamique
translationnelle du fructose (×1,7). La viscosité et la dynamique
témoignent de la structuration en liaisons hydrogène du
mélange, c-à-d de la stabilité de la solution. Lorsque la
température diminue, le bilan total de liaisons hydrogène devient
largement positif, et la solution devient de plus en plus visqueuse. La
solution perd de sa mobilité comme en témoigne la diminution des
coefficients de diffusion de l'eau et du fructose.
| 


