4.1.2. Paramètres expérimentaux
Les gels ont été synthétisés
directement dans des cellules en titane démontables, dans lequel les
échantillons, de 1 ou 2 mm d'épaisseur, sont pris en sandwich
entre deux fenêtres en quartz. Les mesures ont été
réalisées sur l'instrument de diffusion aux petits angles NG-7
30m129 en collaboration avec Drs S. Kline et L. Porcar du NIST
Center for Neutron Research (NCNR, Etats-Unis). Une longueur d'onde incidente
de 6 Å et trois distances détecteur-échantillon de 1, 4 et
13 m ont été utilisées alternativement pour permettre de
couvrir une grande gamme de Q comprise entre 0,0035- 0,47
Å-1.
4.1.3. Mesures préliminaires pour la
détermination des différents contrastes Cette étude va
donc se décomposer en deux parties :
(i) par la détermination du ratio « nul »
H2O/D2O pour atteindre le point de contraste moyen nul, pour lequel le signal
de la silice sera « éteint »,
(ii) par la synthèse de gels pour ce ratio H2O/D2O
particulier afin d'extraire uniquement l'information sur le sucre.
4.1.3.1. Détermination du point de contraste moyen
nul du gel de silice
Les SLD de l'eau légère H2O (SLD (H2O) =
-5×10-7Å-2) et de l'eau lourde D2O (SLD (D2O)
= 6,36×10-6 Å-2) permettent, en
réalisant des mélanges H2O/D2O dans des proportions
définies, d'atteindre la majeure partie des SLD caractéristiques
d'un échantillon. Afin de déterminer la valeur
* Les valeurs des SLD de H2O et de D2O sont très
différentes, ainsi ñ0 peut prendre toutes les valeurs
comprises entre -5× 10-7Å- 2 et 6,36×
10-6Å-2.
de la SLD de la matrice de silice, nous avons
synthétisé six gels de type A1, c-à-d sans sucre, pour les
fractions volumiques H2O/D2O suivantes: 100/0, 80/20, 60/40, 40/60, 20/80 et
0/100. Ainsi, en mesurant ces six échantillons, il nous sera possible de
déterminer avec précision le point de contraste nul pour lequel
le signal de la silice «s'éteint ». Les spectres,
mesurés lorsque le détecteur est à 13 m, sont
présentés sur la figure 40.
1
10
100% H2
40% H
2
20% H2
60% H2
80% H
2
0%H2
O
O
O
O
O
O
0,007 0,01 0,04
Q (+1)
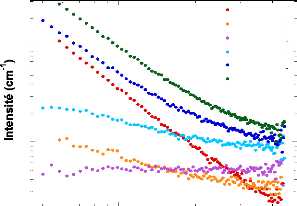
Figure 40: Représentation log-log des spectres SANS des
gels de type A1 synthétisés pour différentes fractions
volumiques H2O/D2O.
Cette série de spectres montre une évolution de
la pente et de la valeur du bruit de fond incohérent pour les plus
grandes valeurs de Q lorsque l'on augmente la proportion d'eau
légère dans le solvant. L'ajout de l'eau légère
fait augmenter la quantité d'atomes d'hydrogène dans le milieu,
et par conséquent le signal incohérent. L'ordre des spectres,
pour Q = 0,04 Å-1, suit bien l'augmentation en proportion de
H2O. La pente, en revanche, évolue de manière non
linéaire: partant d'une pente décroissante (A1 - 0% H2O), elle
passe par une valeur proche de 0 (A1 - 40% H2O) pour enfin redevenir
décroissante (A1 - 100% H2O). Cette variation traduit l'évolution
du contraste du solvant par rapport à celui de la matrice siliceuse. On
en déduit donc que pour un mélange de solvant proche de 40% H2O -
60% D2O, le gel présente une SLD homogène sur l'ensemble de
l'échantillon, ce qui se traduit par un signal plat.
Rappelons ici que l'intensité diffusée est le
carré du module de l'amplitude de diffusion I(Q)A(Q) 2 , et que
l'amplitude A(Q) dépend de la SLD.
Ainsi en traçant la racine carrée de
l'intensité en fonction de la fraction volumique en H2O, il est alors
possible de déterminer le point de contraste nul de la silice. (Figure
41) Nous avons ainsi pu déterminé qu'une fraction volumique
H2O/D2O = 38/62 permet d'éteindre le signal de diffusion de la
silice.
0 20 40 60 80 100
Fraction volumique en H20 (x100)
Figure 41 : Racine carrée de l'intensité
diffusée par le gel A1 en fonction de la fraction volumique en H2O
La densité de longueur de diffusion de la silice peut
donc être calculée avec précision à partir de cette
valeur particulière du pourcentage volumique (%(H2O) = 38), et des
densités de longueurs de diffusion de l'eau légère et
l'eau lourde. Ce calcul conduit à une densité de longueur de
diffusion du réseau de silice égale à SLD (SiO2) = 3,8
Å-2.
| 


