5.2.3. Mesures
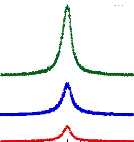
Les fonctions de diffusion des échantillons AT 1, AT2 et
AT3 à 300 K sont présentées sur la figure 57 pour une
valeur de Q = 0,71Å1.
Å1
Q = 0,71
T = 300 K
AT3
AT2
ATI
-150 -100 -50 0 50 100 150
E (peV)
Figure 57: Fonctions de diffusion pour les échantillons
AT1 (rouge), AT2 (bleu) et AT3 (vert) tirées des mesures
réalisées sur le spectromètre IRIS à 300 K.
Les fonctions de diffusion S(Q, E) ont été
ajustées à l'aide de la combinaison de fonctions
théoriques suivantes convoluées avec la
résolution de l'instrument: une fonction delta, une ou deux fonctions
Lorentziennes .L?(Wn,E) suivant la concentration et la
température utilisée, et enfin une ligne de base. Les
informations sur la dynamique translationnelle ont été extraites
de la dépendance quadratique des Wn. Les valeurs des
paramètreset ã1 sont présentées dans le tableau
32.
1 1
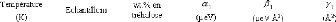



Tableau 32: Valeurs des paramètres d'ajustement pour la
Lorentzienne étroite W1.
0.15
0.1
0.05
0
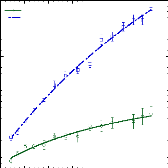
Les ajustements de la fonction Lorentzienne étroite
sont présentés sur la figure 58. L'effet de la concentration en
tréhalose sur la largeur à mi-hauteur W n est
clairement mis en évidence, et montre ainsi le ralentissement des
mouvements diffusifs des molécules de tréhalose.
AT3 - AT1 - 30wt.% of trehalose
AT2 -AT1 - 14wt.% of
trehalose
0 0.5 1 1.5 2 2.5 3 3.5
Q2 (Å2)
Figure 58: Largeur à mi-hauteur de la Lorentzienne
étroite W1 ajustée aux données des soustractions A T2- AT1
etAT3-AT1. Les courbes représentent les ajustements.
Comme nous avons pu le voir dans les paragraphes et chapitres
précédents, les paramètres d'ajustement nous permettent de
remonter aux valeurs des différentes constantes physiques qui
caractérisent le système : le coefficient de diffusion D et la
longueur de saut effective l. Toutes ces constantes sont
répertoriées dans le tableau 33.
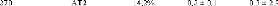
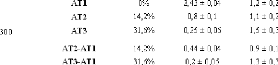

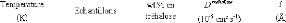
Tableau 33 : Constantes physiques calculées à
partir des ajustements de W1
5.2.4. Résultats et discussions
Tout d'abord, avant de passer à l'interprétation
des constantes physiques proprement dites, il est intéressant de jeter
un oeil sur les valeurs du paramètre d'ajustement 1
de l'échantillon AT2. Il apparaît que 1
présente une dépendance en température qui suit une loi
d'Arrhénius, comme en témoigne la figure 59. L'énergie
d'activation correspondante pour la diffusion translationnelle est de (17,5
#177; 1,7) kJ.mol-1, soit (4,2 #177; 0,4) kcal.mol-1.
Cette énergie est relativement proche de celles trouvées pour des
solutions de D-fructose ((4,0 #177; 0,4) kcal.mol-1) ou pour les
solutions de D-glucose ((3,6 #177; 0,2) kcal.mol-1).76 Ce
paramètre nous donne ainsi un aperçu de l'évolution de la
dynamique du tréhalose en fonction de la température, sans pour
autant être suffisant pour conclure de manière définitive
sur la molécule de sucre. En effet, les gels étant des
systèmes multicomposants, leur étude sans soustraction du gel AT1
ne peut être considérée que comme une approximation. Cette
valeur de l'énergie d'activation doit donc être maniée avec
précaution si l'on parle de la dynamique moléculaire du
tréhalose.
1
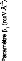
0,01
0,1
0,001
3 3,2 3,4 3,6 3,8
1000/T(K)
Figure 59 : Valeurs de 131
pour l'échantillon AT2 en fonction de 1000/T(K). La droite
représente l'ajustement de la loi d'Arrhénius aux
données.

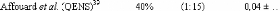
Dtrehalose.
Considérons les valeurs des coefficients de diffusion des
molécules de tréhalose A 300
K, le coefficient de diffusion translationnel diminue d'un
facteur 2 lorsque la concentration passe de
Dtrehalose
14,2 à 31,6wt.%. passe ainsi de 0,42×10-5
à 0,2×10-5 cm2.s-1. Cet
abaissement d'un facteur 2
coïncide avec des travaux réalisés sur des
solutions volumiques de tréhalose.40,62-70,132 Le tableau 34
répertorie tous ces résultats.

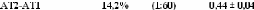
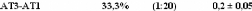
Tableau 34: Comparatif des coefficients de diffusion du
tréhalose confiné (en gras) avec ceux trouvés dans la
littérature.
Si l'on compare nos valeurs avec celles dans la
littérature, nous trouvons qu'il n'existe pas de changements
marqués du coefficient de diffusion translationnelle pour un confinement
estimé à une vingtaine de nanomètres. Ces résultats
viennent d'être très récemment corroborés par des
simulations de dynamique moléculaire réalisées par Drs A.
Lerbret et J.W. Brady de l'Université de Cornell.133
Ce résultat montre qu'un confinement de 20 nm ne semble
pas être suffisant pour affecter de manière significative la
dynamique du tréhalose. Le diamètre moyen des pores est
vraisemblablement trop important. En effet, si l'on ajoute à une
molécule de tréhalose une sphère d'hydratation, son
diamètre moyen atteindra 12-13 Å, une valeur quinze fois
inférieure à la porosité moyenne. Sachant que
l'épaisseur d'une sphère d'hydratation n'est en moyenne que de
5-8 Å, et qu'en milieu dilué, le nombre de sphères atteint
facilement le nombre de 3, une molécule de tréhalose
hydratée mesurera donc au maximum entre 2 et 3 nm, une valeur bien
inférieure au diamètre des pores. Par voie de conséquence,
la dynamique du sucre ne sera que très faiblement affectée par un
tel confinement. Il est intéressant de noter également que cette
conservation de la dynamique implique donc des interactions silice-sucre
relativement faibles, voire négligeables.
| 


