7.2. MESURES ELASTIQUES
7.2.1. Confinement de solutions d' tréhalose
Des scans en énergie à fenêtre fixe ont
été réalisés sur le spectromètre à
rétrodiffusion IN16 de l'Institut Laue-Langevin. Les échantillons
ont été mesurés à une longueur d'onde 2%, = 6,27
Å, pour une résolution en énergie E = 1,2 peV (largeur
à mi-hauteur) et une gamme de Q comprise entre 0,36 et 1,52
Å-1. L'intensité élastique, mesurée en
fonction de la température, est proportionnelle au nombre de diffuseurs
qui ne bougent pas ou qui apparaissent immobiles dans la fenêtre
temporelle correspondante à la résolution du spectromètre
(t < ~ 2 ns).
Les différents échantillons ont
été préalablement refroidis à 10 K et
stabilisés à cette température pendant 30 minutes. La
remontée en température s'est faite ensuite en utilisant une
rampe de 1,4 K/min. entre 10 et 180 K, suivie d'une rampe beaucoup plus lente
(0,4 K/min.) entre 180 et 300 K, pour laisser le temps au système de
s'équilibrer. Les scans élastiques des échantillons
MCM-AT1, MCM-AT2 et MCM-AT3 mesurés entre 10 et 300K sont
présentés dans la figure 74.
0,4
0,3
0,2
0,1
0
0,34
0,32
0,28
0,26
0,24
0,22
0,3
0,2
210 230 250 270
MCM-AT3 (30%)
MCM-AT2 (11%)
MCM-AT1 (D20)
0 50 100 150 200 250 300
T (K)
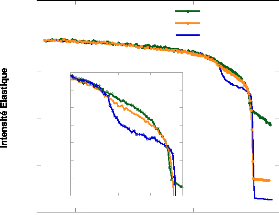
Figure 74 : Scans élastiques des échantillons
MCM-AT1, MCM-AT2 et MCM-AT3 mesurés entre 10 et 300K. L'encart
présente un grossissement de la transition située vers 230 K.
Le spectre de l'échantillon MCM-AT1, déjà
présenté dans le paragraphe précédent, permet de
mieux apprécier les différents régimes thermodynamiques.
(1) A température ambiante, les trois échantillons
présentent un plateau correspondant à l'intensité
élastique du bruit de fond et de la matrice de silice. Les
différences en intensité proviennent des quantités
d'échantillons utilisées, auxquelles s'ajoute l'augmentation du
signal cohérent qui augmente avec la concentration. (2) Vers 270-275 K,
une transition relativement abrupte, liée vraisemblablement à la
fusion du solide non confiné, apparaît. Elle conduit à un
second plateau dans le cas de l'eau lourde ou à une augmentation de
l'intensité élastique dans le cas des solutions de sucre. (3) Aux
alentours de 230-235 K, une seconde transition intervient. Dans le cas de
l'eau, cette transition est bien marquée et assez abrupte. Dans le cas
des solutions de tréhalose, cette transition est beaucoup moins
marquée, et il apparaît que pour des concentrations en sucre
croissantes, cette transition devient de plus en plus graduelle.
Afin de mettre en valeur les différentes transitions et
de déterminer avec plus de précisions leurs positions, nous avons
procédé à un ajustement succinct de ces données par
des fonctions sigmoïdales pour ces trois échantillons. (Figure
75)
(b)
(c)
0,3
(a)
0,35
0,3
0,25
0,2
0,15
MCM-AT1 (D20)
Sigmoide 1
Sigmoide 2
0
0,1
0,05
100 150 200 250 300
T (K)
0,4
0,25
0,2
0,35
0,15
0,1
0,3
0,05
MCM-AT2 (11%) Sigmoide 1 Sigmoide 2
MCM-AT3 (30%) Sigmoide 1 Sigmoide 2
0,25
0
160 180 200 220 240 260 280 300
T (K)
50 100 150 200 250 300
T(K)
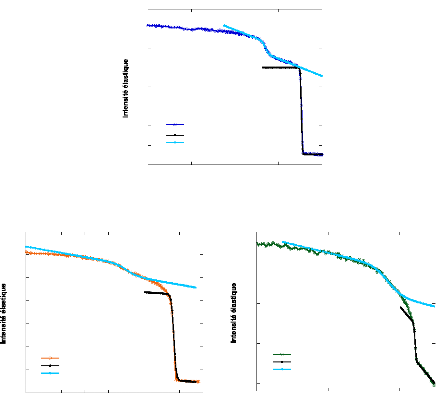
Figure 75: Ajustements des transitions observées dans les
scans élastiques des échantillons MCM-A T1(a), MCM-AT2 (b) et
MCM-AT3 (c). Les fonctions d'ajustements utilisées ici sont des
sigmoïdes.
La fonction sigmoïdale utilisée pour ces ajustements
est donnée ci-dessous :
|
f (x) = A1
|
1+ e-B(x--x0) )
1 )#177; (C --
Dx)
|
dans laquelle les paramètres A, B et x0 ajustent
respectivement la hauteur de la marche, l'aspect plus ou moins abrupte de la
transition, et la position de la transition (au niveau du point d'inflexion).
Le deuxième terme est l'équation d'une droite utilisée ici
pour positionner la sigmoïde en hauteur mais également pour jouer
sur son inclinaison. Les valeurs des paramètres B et x0 sont
présentées dans le tableau 40.

Tableau 40 : Récapitulatif des valeurs des
paramètres x0 et B tirées des ajustements réalisés
sur les transitions observées sur les scans élastiques.

MCM-AT1 (D20)
Deux transitions ont été clairement mises en
évidence par les ajustements présentés sur la figure
75(a). La première, située à T = 277 K, correspond
à la fusion de la glace deutérée volumique,209
alors que la deuxième, aux environs de 235 K, est due à la fusion
de la glace confinée dans les nanopores des
MCM_41.197,198,199,208 (Cf. Chapitre 6) Le paramètre B est
très intéressant, car il donne une information sur le
caractère plus ou moins abrupte de la transition, ainsi, plus B est
grand, plus la transition est abrupte, et inversement, plus B se rapproche de
0, plus elle est graduelle. Ce paramètre témoigne donc de la
coopérativité du système, et donc de son pouvoir à
plus ou moins cristalliser. Il apparaît ici très nettement, que ce
caractère change nettement avec le confinement, puisque B passe de 1,8
à 0,5 lorsque l'on confine la solution dans des pores de 3
nanomètres. Cette chute témoigne donc de la perte de
coopérativité du système, qui passe donc d'un état
cristallisé (T = 275 K) à un état que l'on pourrait
qualifier de vitreux lorsque l'on place la solution dans un état de
confinement (T = 235 K).
MCM-AT2 (11%)
L'ajustement de cet échantillon montre deux transitions
positionnées à 275 et 235 K. (Figure 75(b)) Comme
précédemment, la première est à relier à la
fusion du solide volumique. La transition vers 235 K correspond, quant à
elle, à une température de fusion ou de transition vitreuse,
similaire à celle observée pour l'eau lourde confinée. Le
type de la transition est assez difficile à déterminer pour
l'instant, et des mesures thermiques complémentaires (DSC, ATD) sont
nécessaires. Cependant, l'importante chute de B tend à indiquer
une perte de coopérativité générale par rapport
à la solution volumique, mais également par rapport au D2O
confiné. Ainsi, cette valeur semble montrer que, confinée, la
solution de tréhalose présente plutôt une structure assez
peu structurée, du type verre.
MCM-AT3 (30%)
La figure 75(c) montre une transition à T = 272 K, qui
correspond à la Tfus du mélange D2O/tréhalose
non-confiné. La diminution de 3 K de Tfus, par rapport
à MCM-AT2, est corroborée par le diagramme de phase. (Figure 76)
La seconde transition (234 K), mis en exergue par la sigmoïde, correspond
à la fusion de la glace contenue dans les pores de la silice. Cette
valeur de Tfus est cohérente avec les valeurs
précédentes. Notons également que la
coopérativité du solide confiné semble disparaître
à la vue de la valeur de B dans le cas confiné.
Comparatif de MCM-AT1, MCM-AT2 et MCM-AT3
Si l'on compare les différents échantillons
volumiques, nous remarquons une légère diminution de
Tfus avec la concentration. Maintenant, si l'on regarde le diagramme
de phase du système binaire H2Otréhalose210
présenté en figure 76, nous pouvons remarquer que nos valeurs de
Tfus sont en parfait accord*, dans l'approximation
où le diagramme de phase du mélange D2O/tréhalose
diffère assez peu de celui du mélange H2O/tréhalose.
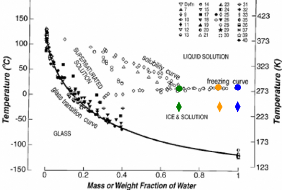
Figure 76 : Diagramme de phase du système binaire
H2O/tréhalose. (? : Tfus des solutions volumiques, : Tfus des solutions
confinées).210
En comparant les différentes valeurs de Tsol
des solutions confinées avec celles des solutions volumiques, nous
trouvons donc une diminution de ~ 40 K dans les trois cas. Il apparaît
donc que le confinement est responsable du décalage en
température de Tsol. Notons également, que la position
du liquidus est décalé vers les plus basses températures
et que sa forme n'est pas modifiée par le confinement. (Figure 76)
Le paramètre B montre une évolution certaine de
la coopérativité du réseau. Pour les solutions
* Nous avons tenu compte du décalage des valeurs de la
température de fusion entre l'eau légère et l'eau lourde.
Le diagramme est utilisé ici uniquement pour connaître
l'évolution générale du liquidus.
volumiques, il présente des valeurs
élevées, attestant de la cristallisation de la solution, alors
que les solutions confinées présentent elles des valeurs beaucoup
plus proches de 0, témoignant de l'aspect plus vitreux du solide
obtenu.
7.2.2. Confinement de solutions de D-glucose
Des scans en énergie à fenêtre fixe ont
été réalisés au NCNR sur le spectromètre
à rétrodiffusion HFBS86. Les échantillons ont
été mesurés à une longueur d'onde 2%, = 6,27
Å, pour une résolution en énergie E = 1,2 peV (largeur
à mi-hauteur) et une gamme de Q comprise entre 0,36 et 1,52
Å-1. L'intensité élastique, mesurée en
fonction de la température, est proportionnelle au nombre de diffuseurs
qui ne bougent pas ou qui apparaissent immobiles dans la fenêtre
temporelle correspondante à la résolution du spectromètre
(t < ~ 2 ns).
Comme précédemment, les échantillons ont
été préalablement refroidis à 10 K, puis
stabilisés à cette température. La remontée en
température s'est faite selon deux rampes : une première de 1,4
K/min entre 10 et 180 K, suivie d'une seconde de 0,22 ou 0,33 K/min pour les
échantillons MCM-A2 et MCM-A3 respectivement. Seule la solution de
glucose (30%) a été mesurée pendant la descente en
température. Les spectres de la solution à 30 % et de MCM-A2 et
MCM-A3 sont présentés dans la figure 77.
(a)
0,9
0,8
0,7
0,6
0,5
MCM-A2
0,4
0,3
(b)
1
0,8
0,6
0,4
Solution 30% MCM-A3
0,2
0 50 100 150 200 250 300
T (K) 0 50 100 150 200 250 300
T (K)
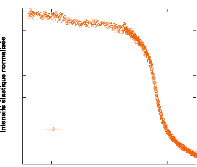
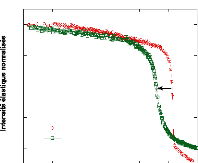
Figure 77: Scans élastiques des échantillons MCM-A2
(a), MCM-A3 et d'une solution à 30% (b) mesurés entre 10 et 300
K.
A la différence des échantillons contenant du
tréhalose, la préparation a permis cette fois d'éliminer
la transition vers 275 K provenant de la fusion de la glace contenue entre les
particules. Seule persiste désormais la transition liée à
la fusion du solide confiné. Comme le signal provient, dans ce cas,
à 100% de la solution confinée, les transitions nous apparaissent
alors plus marquées. A titre comparatif, pour l'échantillon
MCM-AT1, la solution confinée n'était responsable que de 25% de
l'intensité
élastique totale. La figure 77(a) présente
l'évolution de l'échantillon MCM-A2 avec la température.
Une première transition (~ 220-230 K), bien marquée, correspond
à la température de fusion de la glace confinée. Notons
qu'il apparaît entre 50 et 100 K, une deuxième petite chute, dont
l'origine nous est, pour l'instant, inconnue. La figure 77(b) présente
un comparatif de l'échantillon MCM-A3 avec une solution volumique de
même concentration (30%). Il apparaît ici très nettement,
que la réduction d'échelle conduit à un abaissement de la
température de fusion d'au moins de ~ 30-40 K. Pour plus de
précision, nous avons utilisé une nouvelle fois des fonctions
sigmoïdes pour ajuster les transitions. Les ajustements sont
présentés dans la figure 78.
300 0 50 100 150 200 250
300
0 50 100 150 200 250
T (K)
T (K)
0,9
0,8
0,7
0,6
0,5
0,4
0,3
(a)
1
MCM-A2 (11%) Sigmoide
(b)
0,9
0,8
0,7
0,6
0,5
MCM-A3 (30%) Sigmoide
0,4
0,3
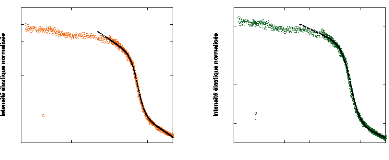
Figure 78 : Ajustements des transitions observées dans les
scans élastiques des échantillons MCM-A2 (a), et MCM-A3 (b). Les
fonctions d'ajustements utilisées ici sont des sigmoïdes.
MCM-A2 (11%)
La sigmoïde s'ajuste parfaitement à la courbe
expérimentale. (Figure 78(a)) La transition a ainsi été
trouvée à T = 231 K. Le paramètre B est égal
à 0,11, une valeur assez proche de celles déterminées pour
le tréhalose, et qui indique une faible coopérativité du
système.
MCM-A3 (30%)
De la même manière, l'échantillon MCM-A3 a
été ajusté à l'aide d'une fonction sigmoïdale
centrée à T = 231 K, et avec un paramètre de
coopérativité B ~ 0,14.
Comparatif MCM-A2 / MCM-A3
Les valeurs de la température de fusion
déterminées pour les deux solutions confinées sont
égales (~ 231 K). A la vue du diagramme de phase
H2O/glucose211 présenté dans la figure 79, nous
pouvons dire que ces résultats suivent la forme du liquidus. Il
apparaît ici, que comme pour les solutions de tréhalose
confinées, la réduction stérique conduit à un
abaissement de la branche du liquidus d'une quarantaine de degré.
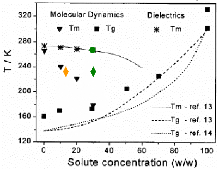
Figure 79: Diagramme de phase du mélange binaire
H2O/D-glucose en fonction de la concentration en monosaccharide. (? : Tfusdes
solutions volumiques, : Tfusdes solutions confinées).211
Comme nous avons pu le voir, dans les différents
chapitres précédents traitant des neutrons, durant
une
expérience de diffusion de neutrons incohérente, la fonction
mesurée est le facteur de structure
dynamique incohérent S inc (Q,), qui
présente deux contributions:
él
- une élastique: S inc Q
( )( , 0)
S inc Q
- une quasi-élastique, qui prend en compte des
énergies ?> 0.
Le déplacement carré moyen, u ,
2 qui prend en compte les fluctuations de toutes les particules
du
système étudié, est donné par:
d S Q
él
{ ln ( ) }
inc
dQ 2
Q 0
2
3
u
Une autre manière donc de déterminer l'existence
de transitions dans un scan élastique est de tracer
les
différentes valeurs du déplacement carré moyen
u2 en fonction de la température.212,213 La figure
80
présente ces tracés pour les échantillons
MCM-A2 et MCM-A3.
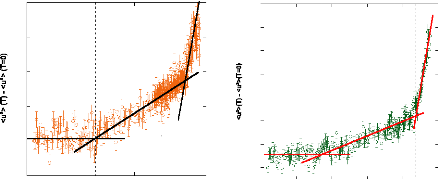
0,4
MCM-A2
0,3
0,2
T1
= 96 K
0,1
0
T 2
= 220 K
-0,1
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
MCM-A3
T1
= 86 K
T2
= 223 K
0 50 100 150 200 250
T(K)
0 50 100 150 200 250
T (K)
Figure 80 : Tracé du déplacement quadratique moyen
<u2> en fonction de T pour les échantillons MCM-A2 et
MCM-A3.
Les tracés ci-dessus montrent l'augmentation des
fluctuations dans le système avec la montée en
température. A basse température, entre 0 et 80 K, les vibrations
sont quasiment nulles, tout le système est figé. Vers 90 K, les
fluctuations atomiques augmentent alors brusquement, indiquant l'apparition
d'une transition. L'augmentation des fluctuations dans cette gamme de
température peut provenir du gain de mobilité de certains
groupements chimiques ou encore d'une transition vitreuse, qui paraît
malgré tout peu probable à ces températures... Si l'on
augmente encore la température, nous trouvons alors une deuxième
cassure assez nette dans les variations de <u2>.
L'augmentation brutale de la pente suggère que les molécules ont
une grande mobilité, comme dans un liquide... Beaucoup plus
marquée que la première, cette transition est due à la
fusion du solide présent dans les pores des sphères de silice. La
différence de température observée avec celles
déterminées avec les ajustements provient du fait que la
température de transition n'a pas été mesurée au
même endroit. Dans le cas précédent, Tfus
était pris au niveau du point d'inflexion, dans ce cas ci, elle a
été mesurée au début de la chute de
l'intensité élastique.

Si l'on regarde maintenant le tracé de u2 en
fonction de la température dans le cas de la solution
volumique à 30% (Figure 81), il est intéressant
de constater qu'une seule et unique transition n'est visible (~ 240 K). Cet
échantillon témoin montre donc que la première transition
n'est observée que dans le cas confiné, et que par
conséquent son origine est vraisemblablement à rapprocher de la
réduction d'échelle. Mais ces seuls résultats, sans
mesures complémentaires, ne nous permettent pas de conclure sur le type
de transition mis en jeu.
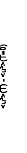
0,28
0,24
0,2
0,16
0,12
0,08
0,04
0
Solution 30%
0 50 100 150 200 250 300
T (K)
Figure 81: Tracé du déplacement quadratique moyen
<u2> en fonction de T pour la solution de glucose à
30%. Une unique transition est visible.
7.2.3. Conclusion
L'étude de la variation de l'intensité
élastique en fonction de la température de ces solutions
confinées a permis de mettre en évidence la présence de 2
ou 3 transitions selon l'échantillon :
- la première vers 270 K correspond à la fusion du
solide non-confiné,
- la seconde vers 230 K correspond à la fusion du solide
confiné,
- la troisième vers 90 K n'a pas encore été
déterminée.
Des mesures thermiques complémentaires (DSC, ATG, ...)
restent malgré tout nécessaires afin d'asseoir nos conclusions
sur les deux premières transitions et de définir l'origine de la
troisième.
Les variations de la dynamique des molécules d'eau et
de sucre en fonction de la température sont directement responsables de
ces transitions. Et une étude complète de la dynamique
moléculaire de ces systèmes par diffusion quasi-élastique
des neutrons va nous permettre d'obtenir quelques indications sur les
changements de propriétés liés à la
réduction de l'espace....
|
|



