II.6.3 Autres considérations
Il est important que le spécimen fabriqué d'un
matériau particulier contienne les unités multiples de sa
structure répétitive pour représenter les
propriétés en bloc .Cette condition est importante dans le cas
des matériaux polycristallins de grand grain, composites
renforcés par des fibres, et matériaux cellulaires. La structure
des matériaux bruts nécessite souvent un plus grand
diamètre de la barre (75-100 mm de diamètre est exigée
pour tester le béton). Les matériaux fragiles, comme les
céramiques, exigent une conception spéciale du spécimen
pour assurer l'uniformité de contrainte avant la rupture. Couque et
autres [64] ont utilisé des spécimens coniques avec anneaux
chanfreinés pour supprimer se division axial en cas des composites
L'utilisation des sections non-uniformes le long du spécimen. La
longueur rend la réduction de données plus complexe La
tolérance sur la géométrie du spécimen est
importante pour assurer une déformation uniforme. Gray III [61] a
mentionné que les faces de chargement du spécimen doivent
être parallèles avec une tolérance de 0.01
millimètre.
II.6.3.1 Considérations spéciales pour les
matériaux doux
C'est bien accepté dans la communauté de
recherche de la barre d'Hopkinson [61] que les méthodes
expérimentales de BPHD et l'analyse des données de 1D sont
généralement valides pour les métaux
élastoplastiques qui satisfont les conditions mentionnées dans la
section, approches de validité de l'essai BPHD. Cependant, des
difficultés additionnelles surgissent dans le cas des matériaux
doux et durs, qui incluent toutes sortes de matériaux technologiques
autres que les métaux élastoplastiques. Le manuel d'ASM [61]
consacre deux
sections séparées à l'essai BPHD; une
pour les matériaux doux [24] et l'autre pour les céramiques [63].
On doit lire ces sections avant de les examiner.
Les matériaux doux incluent une grande
variété de matériaux polymères, mousses des
métaux et des polymères, et des matériaux granulaires.
Sous conditions d'essai de BPHD, Cette classe de matériaux est
caractérisée par leurs très faibles impédances
acoustiques. Elle génère des impulsions transmises très
faibles/faibles si une barre traditionnelle en acier avec un gain
élevé est utilisée. Des chercheurs ont utilisé des
barres de faible impédance (barres en titanium, aluminium et
magnésium [65, 66]) où de bons signaux de transmission peuvent
être obtenus. D'autres ont utilisé des barres polymères
[67-69] (PMMA, PC) pour tester des matériaux doux. L'utilisation d'une
barre polymère exige des analyses additionnelles du comportement
viscoélastique de la barre. Elle ajoute plus de complexité en
comparaison avec les barres métalliques de faible impédance. En
plus des barres pleines métalliques et polymères de faible
impédance, Chen et autres [70] ont utilisé une barre sortante
creuse en aluminium pour obtenir un rapport signal sur bruit mieux que pour les
barres pleines. L'issue principale dans l'essai des matériaux doux est
d'obtenir une bonne impulsion transmise, ce qui peut être
réalisé par l'utilisation des barres de faible impédance.
Cependant, toutes les approches d'équilibre de contrainte, uniforme et
contrainte uniaxiale, effets d'inertie et de frottement, et conditions de
dispersion doivent être satisfaites pour une expérience valide de
BPHD.
La faible vitesse de l'onde dans les matériaux doux
fait le temps de passage dans le spécimen beaucoup plus long que dans
les matériaux métalliques. Ainsi, un spécimen mince est
nécessaire pour satisfaire la condition d'équilibre de
contrainte. D'une part, il est trouvé que le rapport LS/DS
dépend fortement du comportement contrainte-déformation des
matériaux doux [24]. Chen et autres [70] ont observé une
atténuation substantielle de l'onde dans des échantillons
épais en caoutchouc RTV630 (0.25') par rapport aux échantillons
minces (0.06'). Selon la température et le matériau du
spécimen, ils suggèrent qu'un rapport LS/DS de 0.25-
0.50 peut être utilisé pour réduire
l'atténuation.
A raison de la nature viscoélastique de quelques
polymères et composites polymères à la température
ambiante, une procédure spéciale est adoptée au
Laboratoire National de Los Alamos pour usiner des spécimens de BPHD
à surfaces de chargement parallèles avec une tolérance de
0.03 mm [24]. Le spécimen est refroidi à l'azote liquide
au-dessous de sa température de transition vitreuse. Ensuite, il est
usiné dans son état durci; et lentement réchauffé
de nouveau à la température ambiante.
Gray III [61] a suggéré qu'une analyse par
éléments finis de l'expérience de BPHD puisse être
utile en réduisant les données expérimentales avec
confiance, en concevant
l'expérience de BPHD, et en utilisant des techniques
expérimentales de la barre non standard de Hopkinson. Essai de BPHD des
matériaux poreux et granulaires exige des outils diagnostiques
additionnels du spécimen, tels que la photographie ultrarapide et
l'analyse lagrangienne couplée [61].
CHAPITRE III
ANALYSE SPECTRALE DE L'ONDE
III.1 Introduction
L'analyse de la dispersion et de l'atténuation des
ondes est généralement faite par des méthodes spectrales.
Une explication détaillée du changement en domaine
fréquentiel et de la manière de propagation des ondes est
donnée ici. Cette compréhension est fondamentale lors de
l'analyse de la propagation d'onde dans un milieu.
III.1.1 Transformée de Fourier et la
FFT
La transformée de Fourier introduit la notion de
spectre. C'est la caractéristique fréquentielle d'un signal. Ce
dernier peut être défini dans deux espaces, soit temporel ou
fréquentiel. L'analyse spectrale d'une onde périodique complexe
peut être représentée par la superposition d'une
série de sinusoïdes de fréquences reliées
harmoniquement [29]. L'équation générale pour une
sinusoïde harmonique simple est:
f(t) =a 0 +
r1 sin(ù 0 t +
è1) (3.1)
Où a0 est l'excentrée,
r1 est l'amplitude, ù0 est une
fréquence angulaire qui décrit la nature
périodique, et
è1 est l'angle de phase ou le déphasage de
l'onde. L'angle de phase décrit la
quantité de déphasage le long de l'axe de temps de
l'onde. En appliquant l'identité trigonométrique:
r t r t t
1 0 1 1 0 1 0 1
cos( ) [cos( ) cos( ) sin( ) sin( )] (3.2)
ù è ù è ù
è
+ = -
A l'équation (3.1), une forme alternative de l'onde peut
être écrite comme:
f
t a 0 a 1 0 t b 1 0
t
( ) cos( ) sin( )
= + ù +
ù
Où:
a1 = r1
cos(è1) (3.4)
b1 = -r1
sin(è1) (3.5)
Par conséquent, un signal peut être
représenté par une série de Fourier continue écrite
comme:
8
f t a a K k t b K k t
( ) [ cos( ) sin( )]
= + +
? (3.6)
0 0 0
ù ù
k=1
ù0 est la fréquence
fondamentale et k est un nombre entier. Les multiples de fréquence
(kù0)
sont connus comme harmoniques. Une fonction de période
T dans le domaine temporel peut
donc être liée au
spectre de composantes (ak et bk) dans le
domaine fréquentiel. Les figures
III.1a, III.1b et III.1c illustrent comment une onde
carrée peut être décomposée en une
série
d'ondes cosinusoïdales. Si assez de termes sont inclus,
alors la superposition de toutes les
composantes aurait comme conséquence une onde identique
à l'onde carrée.
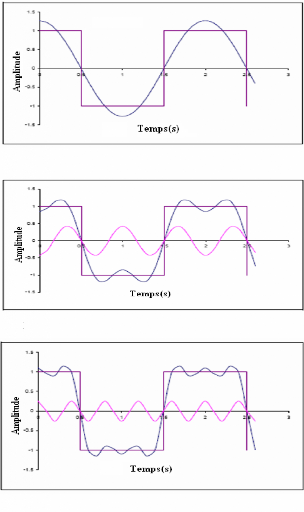
Figure III.1a: Composante de Fourier primaire d'une onde
carrée
Figure III.1 b: Addition de la seconde composante harmonique
Figure III.1c: Addition de la troisième composante
harmonique
En plus de l'amplitude de chacune des composantes de la
série de Fourier, un angle de
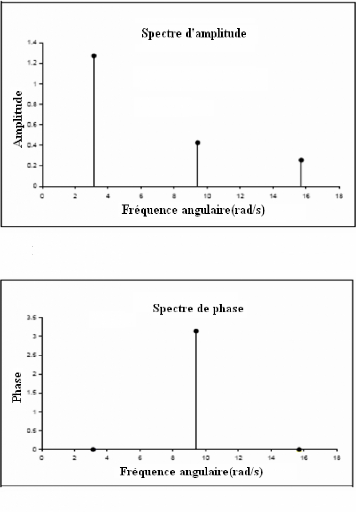
Figure III.2a: Spectre d'amplitude pour les trois premiers
termes
Figure III.2b: Spectre de phase pour les trois premiers termes
phase correspondant doit également exister. Les
spectres d'amplitude et de phase sont nécessaires pour reconstruire
l'onde dans le domaine temporel. Pour l'exemple de l'onde carrée, les
spectres d'amplitude et de phase sont montrés sur les figures III.2a et
III.2b respectivement. En analysant les spectres d'amplitude et de phase un
plus grand aperçu des propriétés de l'onde peut être
eu.
L'analyse ci-dessus a été faite pour un signal
périodique ou répétitif. Cependant, c'est, impraticable
pour analyser la propagation de l'onde puisqu'une onde de contrainte est
apériodique. Pour l'analyse des signaux apériodiques, une
alternative à la série de Fourier a été
développée. Une transformée de Fourier paire permet la
transformation d'un signal apériodique au domaine fréquentiel et
vice-versa. La base de la transformée de Fourier est l'intégrale
de Fourier qui est donnée par:
F ( ) i 0 t
~ 1
= f t e dt
? ù
? + 8 (3.8)
T -8
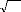
~
|
Où F
|
est la transformée de Fourier continue (TFC),
ù0 est définie avant et i est un
nombre
|
complexe ( -1). L'intégrale de Fourier est
dérivée des séries de Fourier dans sa forme
exponentielle en appliquant les identités d'Euler.
L'application des limites infinies permet la définition d'un signal
apériodique. En d'autres termes, lorsque la période devient
infinie, le signal ne se répète jamais, devenant
apériodique. La deuxième partie de la transformée de
Fourier paire est la transformée inverse qui est donnée par :
f t = F ( ù ) e - i
ù 0 t d ù
? + 8 ~
( ) (3.9)
-8
|
~
Le symbole ~ indique le domaine de fréquence d'une
fonction. F
|
a les composantes réel
|
et imaginaire qui sont liées respectivement aux termes
aK et bK de la série de Fourier. Pour
la
plupart des cas, la fonction f(t) n'est pas connue
analytiquement. Normalement le signal est
connu en termes du signal discret mesuré par un
système d'acquisition de données. Pour ce cas, la
transformée de Fourier discrète (TFD) a été
développée. La TFC écrite en termes des
échantillons (n) donne la transformée paire TFD qui s'exprime par
:
F f e ù pour k à N
~ 0
= - = -
ik n
? 0 1 (3.10)
k n
n = 0
1
0
N - 1
f ù
- ik n =
? = -
0 1
n f n e pour k à N
(3.11)
Nn=0
Où: N est le nombre des échantillons.
Bien que c'est la forme la plus pratique de la
transformée de Fourier, elle exige 2
N opérations complexes ce qui la rend
impraticable manuellement et intimide pour le calcul à l'aide des
ordinateurs. Pour alléger une partie du fardeau de calcul, des
sous-programmes de la transformée de Fourier rapide (FFT) ont
été développés. La plupart des sous-programmes de
FFT réduit 2
N opérations à N log2
(N) opérations, ce qui permet un calcul plus efficace des
coefficients de Fourier. Le lecteur est
référé à Press et autres [30] pour une description
détaillée des sous-programmes de FFT.
|
~
F k
|
a une partie réelle et une partie imaginaire. Alors, il
peut être exprimé en coordonnées
|
|
~
rectangulaires et polaires. En forme rectangulaire,
Fk
~
|
représente les coefficients de la série de
|
|
Fourier. La forme polaire de Fk
|
est liée à la forme rectangulaire par:
|
F k a k ib k re è ~
i k
= + = (3.12)
b
Avec: ( ) tan ( )
2 2 1
-
r a b et k
k k k k
= + =
è
ak

(3.13)
rk est le module et
èk est l'argument (l'angle de phase). Bien que la
plupart des routines
FFT retournent les résultats en forme rectangulaire,
une meilleure compréhension des propriétés de l'onde est
atteinte avec la forme polaire. Quelques considérations spéciales
doivent être prises en considération lorsqu'on passe de la forme
rectangulaire à la forme polaire. Lors de la détermination de
l'angle de phase par la fonction arctan, on doit faire attention que l'angle a
été ajusté à son quart de cercle. La plupart des
programmes mathématiques supposent que l'angle se trouve dans le premier
quart de cercle et ainsi un certain ajustement est nécessaire. L'angle
de phase devrait se situer dans l'intervalle -ð = è
= ð. Aussi bien, les angles de phase doivent être
redéployés "Unwrapped". En redéployant les spectres de
phase, une fonction continue est obtenue en ajoutant ou en soustrayant des
multiples de 2ð quand les sauts absolus entre les spectres
consécutifs de phase sont plus grands que de ð radians (La figure
III.3). Cette procédure compte sur le déphasage relatif à
la première composante ou au terme DC. Le terme DC se produit quand
n = 0 et représente l'aire sous la fonction de temps.
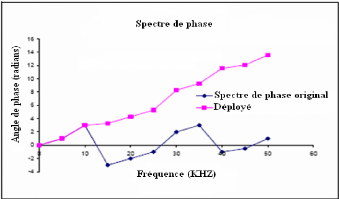
Figure III.3: Redéploiement du spectre de phase
III.1.2 Propagation d'onde dans le domaine de
fréquence
Un des aspects les plus utiles de la transformée de
Fourier est la capacité d'analyser et de prévoir comment les
ondes propageront. Quand une onde propage le long d'une tige, essentiellement
elle est décalée dans le temps. Si une onde carrée simple
est symétrique par rapport le temps zéro, il peut être vu
que la partie imaginaire de la transformée est zéro et qu'il n'y
a aucun déphasage. Si l'onde est déplacée le long de l'axe
de temps, la transformée aura les deux parties; réelle et
imaginaire. La partie réelle est une fonction paire tandis que la partie
imaginaire est une fonction impaire. La figure III.4 montre ces relations pour
une impulsion carrée en utilisant le TFC. En termes de
coordonnées polaires, les amplitudes des impulsions originale et
décalée sont identiques; la seule différence est celle de
la phase. Ceci indique qu'une variation dans le temps correspond à un
changement de phase dans le domaine de fréquence. Ceci mène
à la relation suivante:
f t t F e r e n
( ) ( ) 0 0 0 0
- = ù - = -
i t
ù è ù
i t
( ) (3.14)
0 n n
Où t0 est la quantité de
variation dans le temps.
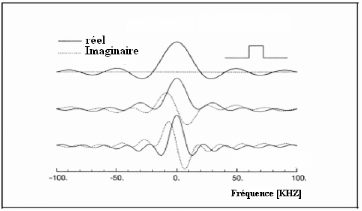
Figure III.4: Composantes réelle et imaginaire pour une
impulsion carrée soumise à des quantités
différentes de déphasage, Doyle [31]
Connaître la manière de propagation d'une onde
dans un matériau est d'importance primordiale dans l'analyse d'onde. La
dispersion et l'atténuation de l'onde peuvent avoir lieu lorsqu'elle se
propage dans certains milieux. La dispersion est liée à
l'allongement d'une onde pendant la propagation dans un milieu tandis que
l'atténuation est liée à une réduction d'amplitude.
La dispersion et l'atténuation sont des actions en corrélation
qui sont généralement
couplées. En d'autres termes, s'il y'a dispersion, il
y'a généralement atténuation. La figure III.5 montre ces
effets. L'atténuation et la dispersion peuvent être
provoquées par une variété de facteurs comme, les
propriétés du matériau et les contraintes
géométriques. La capacité de séparer les
composantes d'une onde est une clé pour analyser les relations de
dispersion et d'atténuation. La figure III.6 illustre les composantes
d'une onde en fonction du temps. Le train d'ondes du côté gauche
illustre un système non dispersif. Pendant la propagation d'onde, ses
différentes composantes ont la même vitesse et gardent donc dans
la même position relative entre elles. Ceci signifie qu'à tout
moment donné l'addition des différentes composantes de l'onde
aura comme conséquence la même onde. Pour le système
dispersif, montré à droite du de la figure III.6, les trains
d'onde ont différentes vitesses ce qui change leurs positions relatives.
Ceci signifie que pendant la propagation du train d'ondes, l'onde
résultante se déformera avec le temps. La vitesse de
déplacement de chaque composante s'appelle la vitesse de phase. Elle qui
est donnée par:
x ù
c= = (3.15)
t k
Où c est la vitesse de phase, t est le temps, x est la
distance mesurée à partir de l'interface et k est le nombre
d'onde. En reliant la vitesse de chaque phase à la fréquence, un
rapport dispersif peut être développé [31, 32, 33]. Le
rapport entre le nombre d'onde et la fréquence s'appelle le rapport de
spectre. La vitesse à laquelle l'onde superposée se
déplace s'appelle la vitesse de groupe (cg). C'est
l'onde actuellement observée.
Si l'onde est mesurée en un point, alors elle peut
théoriquement être prévue à un autre point en
appliquant une fonction de transfert à l'onde originale. En d'autres
termes, si on sait le rapport dispersif, on peut prévoir comment une
onde propagera à travers un matériau.
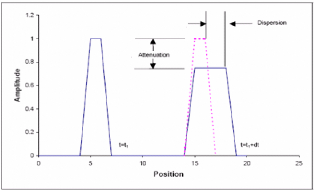
Figure III.5: Illustration des effets de la dispersion et de
l'atténuation [2]
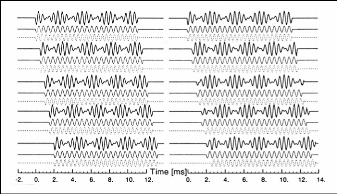
Figure III.6: Segments d'un train infini d'ondes à
différentes positions.
Gauche: Système non dispersif. Droite:
Système dispersif, Doyle [31]
III.1.3 Équations d'onde
Afin de prévoir l'état de propagation d'une onde
dans un milieu, un modèle décrivant son mouvement doit être
formulé. Le développement des équations de
fréquence de Pochhammer [34] et de Chree [35] forme la base pour
l'analyse de la propagation longitudinale d'onde. Ces équations relient
la vitesse de phase à la fréquence pour une propagation
unidimensionnelle de l'onde. Selon Follansbee [36] une analyse
unidimensionnelle est suffisante puisque la majorité de l'énergie
est contenue dans les longueurs d'onde qui excèdent dix fois le rayon de
la barre. Ceci signifie également que la mesure extérieure de la
contrainte est un indicateur valide de déplacement axial.
L'équation unidimensionnelle du mouvement d'onde est:
2 ? 2
? u u

T = ñ (3.16)
? x
2 t 2
?
Où T est la force de tension axiale dans le
matériau et ñ est la densité.
Le changement au domaine de fréquence et la
résolution de (3.16) donne:
u x t u x F n G K mn x e
= = ?
~ i nt
ù
( , ) ( , ù ) ( )(3.17)
Où Fn est le spectre d'amplitude et
le G est la fonction de transfert du système; Doyle [31].
L'indice inférieur m se rapporte au mode de la
solution. Généralement, seulement le premier mode est
considéré; Cheng et autres [38]. La fonction de transfert
détermine la quantité d'atténuation du déphasage en
fonction de l'espace. On verra plus tard que la fonction de transfert sera
liée au coefficient de propagation ã.
On considère un matériau élastique
analysé linéairement. La dispersion est ignorée si le
rapport de la longueur d'onde (ë) au rayon (R) est
beaucoup moins à l'unité; Davies [4].
Follansbee et Frantz [32] ont déterminé que la
dispersion est une considération importante même lorsque
ë/R << 1 pour les barres linéairement
élastiques.
Les effets viscoélastiques créent des
problèmes avec les barres polymères. L'utilisation des barres
fabriquées de ces matériaux exige une plus grande
compréhension des propriétés du matériau de la
barre. L'atténuation et la dispersion ont de grands effets sur les
ondes; incidente, réfléchie et transmise. Le problème est
que la mesure de la jauge de contrainte au milieu de la barre ne correspond pas
aux conditions à l'interface barre-spécimen. Par
conséquent, la réduction de quelques données est
exigée. Une variété de méthodes a été
suggérée pour combattre ce problème.
III.2 Méthodes de correction de la dispersion et
de l'atténuation
La correction de la dispersion améliore la forme de la
courbe contrainte-déformation dynamique [53]. Des méthodes
expérimentales et théoriques sont à utiliser pour corriger
la dispersion et l'atténuation d'un signal.
III.2.1 Méthodes analytiques
L'approche théorique pour résoudre ce
problème exige qu'un modèle viscoélastique du
matériau soit formulé. Le modèle est utilisé pour
simuler le comportement du matériau de sorte que l'onde puisse
être prévue à un certain point de mesure connue. Kolsky
[39] illustre les trois modèles les plus généralement
utilisés pour simuler la réponse viscoélastique. Les trois
modèles, représentés sur la figure III.7, sont
composés d'éléments amortisseur et ressort. Les
différentes configurations de Voigt, de Maxwell et du Solide
général modélisent les différents types de
comportements dynamiques. Le modèle de Voigt est fondé sur
l'hypothèse que les composantes de la contrainte dans un solide sont
proportionnelles à la somme de la déformation et du taux de
déformation. Dans le solide de Maxwell, le taux de contrainte est
proportionnel au taux de déformation et à la contrainte. Alors,
les solides de Maxwell et de Voigt réagissent de manières
opposées. On a une décroissance logarithmique inversement
proportionnelle à la fréquence dans l'amplitude de la vibration
pour des solides de Maxwell et directement proportionnelle pour des solides de
Voigt. Le modèle le plus général est une combinaison des
éléments de Maxwell et de Voigt. Le résultat est un
modèle qui est plus utile en décrivant la nature qualitative du
matériau viscoélastique. Cependant, même le modèle
général ne correspond pas bien aux résultats quantitatifs
exceptés sur une petite gamme de fréquence. Wang et autres [40]
proposent que le
modèle non linéaire de Zhu-Wang-Tang (ZWT)
puisse simuler le comportement viscoélastique des matériaux
polymères. Le modèle de ZWT est une compilation de deux solides
de Maxwell parallèlement à un ressort. Par simulation
numérique, ils peuvent prédire précisément la
réponse viscoélastique connaissant les propriétés
du matériau.
Tyas et Watson [41] utilisent la simulation numérique
pour déterminer le comportement viscoélastique d'un
matériau. Ils simulent l'historique d'une force d'entrée
appliqué à l'extrémité d'une barre tout en
enregistrant le signal dispersé à une certaine distance de
l'extrémité. A partir de l'entrée connue et la sortie
enregistrée, le rapport dispersif peut être
déterminé.
Sawas et autres [42] ont utilisé des barres en
acrylique pour examiner des échantillons en polycarbonate, mousse de
polyuréthane et mousse de styrol avec un certain succès. Leur
méthode de réduction de données exige une connaissance a
priori des propriétés du matériau des barres acryliques.
Ces propriétés sont utilisées pour résoudre une
forme de l'équation d'ondes viscoélastique permettant à la
propagation de l'onde d'être prévue.
Zhao et Gary [43] ont développé une
équation d'onde tridimensionnelle basée sur l'équation de
propagation de l'onde longitudinale de Pochhammer et Chree. Par comparaison
avec des résultats empiriques, ils prouvent que l'application du
modèle tridimensionnel prévoit plus exactement l'état de
propagation des ondes dans des milieux viscoélastiques. Zhao et Gary
[44] ont également étendu ce travail afin d'inclure une
méthode inverse pour le calcul des paramètres du matériau.
En mesurant la vitesse sur les extrémités de la barre et puis en
estimant les paramètres modèles par des itérations
multiples. Sogabe et autres [45] emploient une approche semblable pour
définir un coefficient de propagation qui permet la correction de
l'atténuation et de la dispersion.
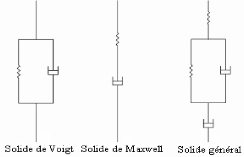
Figure III.7: Modèles des solides
viscoélastiques
III.2.2 Méthodes expérimentales
L'avantage de déterminer les propriétés
du matériau des barres; entrante et sortante expérimentalement
est qu'aucune connaissance antérieure des propriétés du
matériau n'est exigée et ce n'est pas nécessaire de
résoudre les équations de fréquence de Pochhammer et de
Chree. Aussi bien, les corrections basées sur des techniques analytiques
semblent limitées à corriger seulement un peu de distorsion
dispersive.
Gorham et Wu [33] ont suggéré une méthode
pour déterminer expérimentalement les corrections de phase. Leur
méthode exige qu'une série d'essais à l'aide de
projectiles de différentes tailles soit effectuée. Le spectre de
phase pour chaque impulsion est analysé et avec la connaissance de la
manière dont une impulsion idéale propage, la variation de la
phase fondamentale commune à toutes les courbes est
déterminée. Avec la connaissance de la façon dont les
vitesses de phase changent sur la gamme des fréquences, la dispersion de
l'onde peut donc être prévue.
Bacon [46] suggère une méthode
expérimentale pour considérer l'atténuation et la
dispersion dans les barres viscoélastiques. Cette méthode
implique de réaliser un essai sur chaque barre afin de déterminer
le comportement du matériau viscoélastique. Cette méthode,
décrite plus tard, détermine le rapport dispersif
expérimentalement. Bacon et Brun [47] ont étendu cette
méthode pour déterminer le rapport dispersif sur la longueur des
barres non uniformes. Cette méthodologie serait utile si les
extrémités des barres sont chauffées ou si les barres sont
d'impédance non uniforme pour assortir un échantillon. Ce travail
est une prolongation de Lundberg et autres [48] où les
propriétés viscoélastiques du matériau ont
été déterminées en utilisant une technique de
mesure à deux points. Cheng et autres [38] suggèrent une
méthode semblable de détermination du coefficient de propagation.
Au lieu de redéployer les spectres de phase pour déterminer le
déphasage entre deux impulsions, le nombre d'onde est estimé pour
donner une vitesse de phase et un rapport de fréquence raisonnables.
III.2.2.1 Théorie derrière la
méthode expérimentale
En appliquant l'analyse spectrale de l'onde à une
configuration de la barre d'Hopkinson, des équations reliant la vitesse
et la force aux interfaces de la barre peuvent être
dérivées. L'équation d'ondes unidimensionnelle peut
être écrite en terme de contrainte comme:
? ó
( , ) 2 ( , )
x t ? x t
= ñ (3.18)
2
? t
x ?
La déformation est liée au déplacement
par:
? u x t
( , )
å( , )
x t = (3.19)
? t
En écrivant ces équations d'ondes de base dans le
domaine de Fourier:
? 2
ó x ù ñù å x
ù
~ 2 ~
? x 2
( , ) = - ( , ) (3.20)
Où ( , )
ó ~ x ù et å x ù
sont les transformées de Fourier de la contrainte et de la
déformation ~
( , )
respectivement. La fréquence angulaire ù
est reliée à la fréquence par: ù =
2ðf .Pour des milieux linéairement viscoélastiques,
la contrainte est donc liée à la déformation par:
ó ~ x ù = E ù å
x ù
( , ) * ( ) ~ ( , ) (3.21)
Où E * est le module complexe du matériau.
Le coefficient de propagationã =
ã(ù), est défini par:
2
ñ . ù
ã
=
2 (3.22)
E * En utilisant les
équations (3.20), (3.2 1) et (3.22) l'équation unidimensionnelle
d'un mouvement
2
~
axial devient:
? ã å ù
å ù x
( , ) ~
x
+ =
2 ( , ) 0 (3.23)
dx
2
La solution générale de cette équation est
donnée comme:
~ = - +
~ ã x ~ x
x P e N e ã
å ù ù
( , ) ( ) ( )
ù(3.24)
~ ~
Où: ( )
P ( )
ù et N ù sont les transformées
de Fourier des déformations à x = 0 .Elles sont dues
à la propagation des ondes dans les directions de l'augmentation et de
diminution de x respectivement. La vitessev ( , )
~ x ù , et la force normale
F(x,ù), sont alors:
~ = - ? - - x
i ù ~ ã x ?
v( , ) ~
x P e N e ã
ù ( )
ù ( ù )(3.25)
ã ?? ??
|
~ ñ ù
A
F x
( , )
ù = - ã 2
|
2 ? - + x
~ ã x ~
P e N e ã
( )
ù ( )
ù
??
|
?
??
|
(3.26)
|
Le module et l'angle de phase des fonctions exponentielles
complexes x
e -ã et x
eãsont liés à
l'atténuation et à la propagation respectivement. Le coefficient
de propagation ã(ù) est lié au
coefficient d'atténuationá(ù), et
à la vitesse de phase c(ù) par:
ù
ã ù á ù ù á
ù
( ) ( ) ( ) ( )
= + i K = + i (3.27)
c ( )
ù
Où: K(ù) est le nombre d'onde
(fonction impaire) et á(ù) est également
une fonction positive avec : á(0) = 0.
III.2.2.2 Détermination expérimentale du
coefficient de propagation
La méthode suivante est basée sur le travail de
Bacon [46]. La base de la détermination
deã(ù) expérimentalement est
l'équation (3.26). En permettant à une extrémité de
la barre d'être
libre; la force devient zéro (ou bien au moins très
petite que la force à l'endroit de la jauge de déformation).
Lorsque la force à l'extrémité est zéro,
l'équation (3.26) deviennent:
Pe - ã d Ne ã d
~ + ~ = 0 (3.28)
|
~
Où: d est la distance de l'endroit de la jauge de
déformation à l'extrémité libre et P
|
~
et N
|
sont liés
|
|
~
|
|
aux déformations incidente et réfléchie par:
I P et R N
å ~ = å ~ = (3.29)
La fonction de transfert G(ù)peut alors
être définie comme:
~
|
G R e 2
( ) ã
ù -
å ù
~ ( )
= - =
d
å ù
~ I ( )
|
(3.30)
|
Le signe négatif devant le rapport doit compenser le
fait que l'onde réfléchie est inversée. Il devrait
être appliqué à la transformée de Fourier de la
déformation réfléchie en forme rectangulaire. Alors, le
rapport complexe décrit comment l'onde a changé, à raison
de l'atténuation et de la dispersion, sur la distance 2d. Après
qu'un signe négatif soit appliqué à la déformation
réfléchie, le rapport complexe devient:
= è - è = - ã = -
á +
r
G R I
R e e e
i d iK d
( ) 2 ( ) 2(3.3 1)
rI
L'égalisation de la partie réelle et imaginaire
donne:
? r ?
? ?
ln R
? r I ?
á = ? (3.32)
2
d
k
()
? è I
è R
2 d
Ceci est fait pour chaque fréquence. Par
conséquent, le rapport dispersif entre la fréquence et le k est
déterminé.
La détermination du coefficient de propagation permet la
détermination de la vitesse et la
force à l'interface des barres incidente et transmise.
Ceci, alternativement, permet un calcul direct du taux de déformation de
l'équation (2.1). La contrainte peut être calculée à
partir:
F ( t )
ó =
T (3.33)
S A
S
Où les indices inférieurs S et
T se rapportent au spécimen et à la barre transmise
respectivement. La déformation peut être déterminée
en intégrant l'équation (2.1) par rapport au temps comme suit:
å S =? å & S dt (3.34)
La division de la longueur de l'échantillon pour
obtenir le taux de déformation et la section de l'échantillon
pour obtenir la contrainte devrait être faite dans l'ordre de domaine de
temps pour maintenir sa représentation physique.
III.3 Conclusion
Ce chapitre a décrit la base de l'analyse spectrale de
l'onde comme elle s'applique à l'appareil à barre d'Hopkinson. La
compréhension de cette méthode d'analyse de propagation d'onde
permet d'inclure un rapport dispersif qui permet d'analyser le comportement
viscoélastique inhérent à la plupart des polymères.
En plus d'une analyse détaillée d'une méthode
expérimentale, de diverses méthodes analytiques pour la
détermination du rapport dispersif ont été
également discutées.
| 


