Les AVC au Maroc: etude des maladies à risque et analyse des déterminants du degré d'handicap

II.2.3. LES RESULTATS DES ESTIMATIONS DES MODELES EXPLICATIFS DE LA SURVENANCE DES MALADIES A RISQUE

Dans cette partie nous allons présenter et analyser les résultats de chaque modèle (modèle de base) ensuite affiner le traitement en spécifiant le sexe dans chaque modèle. Nous allons effectuer une régression avec Logit simple, puis calculer les effets marginaux et enfin les rapports de côtes.

A/ L'application du logit simple

Nos variables à expliquer (HTA, DIABETE et CARDIAQUE) sont toutes qualitatives binaires codées 1 si l'individu est exposé à la maladie et 0 si non. C'est la raison pour laquelle nous allons utiliser la régression logistique. La fonction logistique est définie par :

F(x) = 1 / (1 + e^-x)

Cette fonction est bien adaptée à la modélisation de probabilités car elle prend ses valeurs entre 0 et 1 selon une courbe de S. Elle est très utilisée lors de la modélisation du risque individuel de développer une maladie.

Concernant les coefficients issus de cette régression, ils n'ont pas la même signification que ceux d'un modèle linéaire simple estimé par les MCO. Pour les coefficients obtenus par une estimation par la méthode du maximum de vraisemblance seul leurs signes sont interprétables.

Nous allons estimer le modèle de base et présenter ses résultats ensuite, pour affiner les résultats nous allons estimer le modèle en spécifiant le sexe. Le tableau ci-dessous est élaboré pour présenter les résultats obtenus.

31

TABLEAU 12: RESULTATS DE LA REGRESSION AVEC LOGIT SIMPLE

Les variables explicatives	Sexe confondu			Hommes			Femmes
	HTA	Diabète	MC	HTA	Diabète	MC	HTA	Diabète	MC
	-0.0193606	0.0094989	-0.0293392	0.0136344	0.0437251	0.0075534	-0.0165736	-0.0188073	-0.0390999
Educ
	(-3.80)	(1.54)	(-3.67)	(1.68)	(5.12)	(0.65)	(-2.52)	(-2.05)	(-3.55)
	0.0533932	0.0520336	0.0401499	0.0592349	0.0575523	0.0499085	0.0569493	0.0492787	0.038796
Age
	(41.97)	(36.61)	(20.32)	(25.38)	(25.98)	(13.70)	(34.59)	(25.94)	(16.12)
	0.2110683	0.2273403	-0.1159997	0.1953259	0.2147843	-0.1623968	0.2553194	-0.2025039	-0.1304111
Tabac
	(2.93)	(2.77)	(-0.49)	(2.42)	(2.51)	(-1.11)	(0.70)	(-0.41)	(-0.24)
	-0.1639639	0.1365691	-0.3684601	-0.1861749	0.0499531	-0.3175045	0.1479255	0.3669153	-0.2193176
Sport
	(-1.81)	(1.36)	(-2.37)	(-1.41)	(0.38)	(-1.56)	(1.15)	(2.27)	(-0.89)
		1.043213	1.194082		1.255955	1.292978		0.8652625	1.054412
HTA
		(15.47)	(15.38)		(11.25)	(9.05)		(10.20)	(11.42)
	1.091669		0.6307052	1.344118		0.574028	0.893629		0.6245713
Diabète
	(16.59)		(6.64)	(12.49)		(3.51)	(10.71)		(5.39)
Maladies	1.178567	0.5302503		1.270314	0.4359439		1.03245	0.5476356
Cardiaques	(14.55)	(5.26)		(8.52)	(2.50)		(10.71)	(4.48)
Nb d'obs	43 626	43 626	43 626	21 247	21 247	21 247	22 379	22 379	22 379
Pseudo R^2	0.1804	0.1480	0.1378	0.1903	0.1579	0.1451	0.1769	0.1435	0.1294

Nous avons les coefficients de chaque variable et entre parenthèses les t-student.

32

L'application du logit simple au niveau des différents modèles, nous donne des R² compris entre 12.94% et 19.03%. Ce faible seuil est toujours le cas des estimations sur données individuelles. On obtient un R² du modèle HTA toujours supérieur à celui des autres modèles, au niveau de la population globale mais aussi dans les modèles avec spécification du sexe. Le modèle à variable explicative « HTA » explique 18.04% de la variabilité entre individu du risque HTA²².

Concernant le modèle à variable explicative HTA : toutes les variables sont significatives quand l'estimation se fait sur la population globale sans distinction du genre. Les signes des coefficients des variables explicatives sont exactement à quoi on s'attendait. La variable Sport devient non significative pour les hommes et le niveau d'éducation change de signe (passant de négatif à positif). Le niveau d'éducation des femmes agit significativement sur la survenance de la maladie HTA, de la même façon que celui sur la population globale. Seul le Tabac et le Sport deviennent non significatifs chez les femmes.

Pour le modèle à variable explicative DIABETE : les variables Niveau d'éducation et Sport ne sont pas significatives, pour le modèle estimé sur l'ensemble des iindividus. Quand on estime le même modèle mais en distinguant le genre, le niveau d'éducation devient significatif mais avec des signes différents. Il agit négativement sur la survenance du Diabète chez les femmes par contre chez les hommes, leur niveau d'éducation agit positivement.

Le Sport reste non significatif chez les hommes, contrairement chez les femmes mais avec un mauvais signe (agit positivement sur la survenance du diabète). Cependant le Tabac est non significatif chez les femmes.

Concernant le modèle à variable explicative les MC²³ : toutes les variables explicatives agissent significativement sur la survenance des maladies cardiaques au niveau de la population globale sauf pour la variable Tabac. Cette dernière reste non significative chez les hommes et les femmes plus le sport. Par contre le niveau d'éducation agit négativement et significativement sur la survenance des maladies cardiaques chez les femmes mais devient non significatif chez les hommes.

La non significativité de la variable Tabac chez les femmes dans tous les modèles, peut être expliquée par les caractéristiques socioculturelles et religieuses du Maroc. En effet, la réponse des femmes enquêtées concernant cette question ne reflète pas la réalité. Nous n'avons obtenus que 0.37% des femmes qui fument contre 16.1% des hommes.

Le sport doit agir négativement sur la survenance des maladies à risque AVC, or nous avons remarqué que cette variable agit significativement et positivement sur la survenance du

²² La taille de l'échantillon permettrait d'introduire plus de variables, dans le cadre des travaux ultérieurs.

23 Les maladies cardiaques

33

Diabète chez les femmes. Du point de vue médical, la pratique du sport n'agit pas sur la probabilité de la survenance du Diabète. Les antécédents familiaux et la nutrition²⁴ agissent en premier sur l'exposition à cette maladie, malgré la pratique du sport.

On s'attendait à ce que le niveau d'éducation agit négativement et significativement dans tous les modèles (le fait d'avoir un niveau d'éducation supérieur diminue la probabilité d'avoir les maladies à risque AVC). Or, nous pouvons expliquer la non significativité de cette variable dans certains modèles par sa distribution.

^{Kernel density estimate}

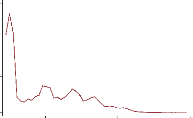
^{0 5 10 15 20 25}

^{nombre d'années scolaires}

^kernel = ^{epanechnikov, bandwidth} = ^0.4851

L'étude de l'aplatissement et l'aplanissement du niveau d'éducation au niveau de la population globale nous permet d'avoir deux coefficients :

Skewness= 0.6960795 et Kurtosis= 2.422271 Cette variable a donc une distribution²⁵ plus pointue que la loi normale centrée réduite, décalée à gauche de la moyenne avec une

queue de distribution étalée vers la droite. Figure 2: La distribution du niveau d'éducation

La signification de la distribution de cette variable nous permet de conclure qu'une part importante de la population a un faible niveau d'éducation. Ce qui implique une relative faible variabilité du niveau d'éducation et donc de sa non significativité dans certaines estimations.

Récapitulons les résultats, le niveau d'éducation impact différemment sur chaque maladie à risque et aussi différemment pour les hommes que pour les femmes. Le niveau d'éducation des femmes agit négativement et significativement sur la survenance des trois maladies à risque. Il en est de même des modèles sans distinction du genre (l'HTA et MC sont significatifs à 1%) sauf pour le Diabète.

₀

Cette même variable ²⁶ agit positivement et significativement sur la survenance des deux maladies à risque d'AVC chez les hommes (HTA et Diabète), elle est non significative pour les maladies MC. Cette différence dans les résultats peut être expliquée, du fait que les femmes les plus éduquées soignent plus correctement les maladies à risque d'AVC en suivant un régime et en prenant régulièrement les médicaments appropriés que les hommes du même niveau d'éducation. Les femmes éduquées sont plus vite sensibilisées au maintien d'une bonne hygiène de vie. Au niveau de la population dont le niveau scolaire est le secondaire et plus,

²⁴ Possibilité d'introduire les variables en lien avec la nutrition comme la quantité de sel consommée et le régime méditerranéen dans des travaux futurs.

25 On obtient la même distribution quand on spécifie le sexe (H ou F)

²⁶ Le niveau d'éducation est une variable quantitative. Nous avons essayé d'effectuer les estimations ont transformant le niveau d'éducation en variable qualitative à trois modalités : aucun niveau, niveau primaire puis secondaire et plus avec le niveau primaire comme modalité de référence. Nous avons obtenus les mêmes résultats que ceux de la variable quantitative.

34

20% des femmes pratiquent le sport (Dans la population avec aucun niveau scolaire, seulement 0.80% des femmes pratiquent le sport).

Cette explication n'est pas valable pour les hommes. Le fait que le niveau d'éducation agit positivement sur la survenance des maladies à risque d'AVC peut être expliqué que l'effet revenu l'emporte sur l'effet éducation. Lorsqu'il y' a une augmentation du revenu, les marocains changent d'habitude alimentaire et ont tendance à plus consommer (viande, gâteaux...). Ainsi le niveau d'éducation ne suffit plus à contrecarrer les mauvais comportements.

Nous allons calculer les effets marginaux (EM) dont les résultats sont présentés dans le tableau ci-dessous. Les signes des coefficients ne changent pas après calcul des EM.

35