Enrichissement du milieu et persistance des espèces dans les cha??nes trophiques : apport de la théorie DEB

Modèles et méthodes

1 Le modèle de Rosenzweig - Mac Arthur

Le modèle de Rosenzweig - Mac Arthur (R-M) est un modèle initialement a deux équations décrivant les interactions non spatialisées entre une proie et un prédateur (Rosenzweig & MacArthur, 1963). Historiquement, ce modèle fût utilisé pour mieux comprendre la dynamique induite par les relations de prédations dans l'écosystème. Il a ensuite été modiflé pour décrire les chalnes trophiques a trois échelons observées dans le milieu. Ce type de modèle très simple s'appuie sur de nombreuses hypothèses, dont entre autres :

- milieu de richesse constante

- prédateur monospécifique

- pas d'interactions avec d'autres espèces

- mortalité des proies négligeable par rapport au taux de prédation

- pas d'interaction des prédateurs entre eux (poursuite de la même proie)

- facteur de conversion de biomasse de proie en biomasse de prédateur constant Cette simplicité en permet une étude mathématique poussée et le rend comparable aux milieux expérimentaux contrôlés de type chemostat.

Dans la formulation mathématique de ce modèle de chalne trophique (Fig. 1), X1 représente la biomasse des proies, X2 celle des prédateurs et X3 celle des superprédateurs. La croissance des proies s'effectue selon la fonction logistique r X1 (1 - X1 _K ) oü r et K sont respectivement le taux de croissance et la capacité limite du milieu pour la population de proies. La prédation du prédateur (i = 2) comme celle du super-prédateur (i = 3) suit une réponse fonctionnelle de Holling

type _IIaiXi-1

bi+Xi-1 oü a et b sont respectivement le taux maximum de prédation et la constante de demi-saturation en proies. L'efficacité de la conversion d'un échelon trophique en l'échelon supérieur est déterminée par le coefficient e , supposé constant. La mortalité est considérée comme un phénomène linéaire ou la biomasse d'individus qui meurent est proportionnelle a la biomasse totale selon un taux d (Tab. 1).

MOdèlES ET méThOdES

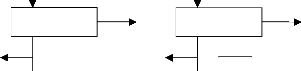
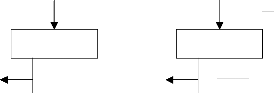
FIG. 1 - Correspondance entre les processus a l'oeuvre au sein de la chalne trophique et leur formulation dans le modèle de R-M a trois échelons.

TAB. 1 - Interprétation des variables d'e'tat et des paramètres du modèle de Rosenzweig - Mac Arthur avec comme dimension M pour les masses et T pour le temps et valeurs prises par ces paramètres.

Notation	Interprétation	Dimension		Valeur i=(2,3)		r
taux de croissance des proies	T-1	i = 2		i = 3	K
capacité limite pour les proies	M	variable		X
biomasse de proie (i=1), de prédateur	M	-		-
(i=2) ou de superprédateur (i=3)					a
taux de prédation maximum du ^iièmeéchelon	M.T^-1	5/3		0,05	b
constante de demi-saturation de la pré- dation de i sur i-1	M	1/3		0,5	e
efficacité de la conversion entre l'éche- lon i-1 et l'échelon i	-	1		1	d
taux de mortalité du ^iièmeéchelon	T-1	0,4		0,01

Les variations de chaque compartiment du système peuvent ensuite être traduites en termes d'e'quations diffe'rentielles³ en faisant précéder les apports d'un signe positif et les pertes d'un signe négatif. On doit en outre remarquer que le terme qui est prélevé par la prédation ne correspond pas a ce qui est intégré dans l'échelon trophique supérieur du fait de l'introduction de l'efficacité de conversion: il y a une possibilité de perte d'énergie le long de la chalne trophique. Il en résulte le système d'équations différentielles suivant :

dX1 dt

dX2 dt dX3 dt

X1 a2 X1

=rX1(1-- _K) -- X2 (1a)
^b2+^X1

^a2^X1 a3 X2

= e2

= e3

^X2--d2^X2-- X3 (1b)

b2+^X1 b3+^X2

^X3^--d3^X3 (1c)

3+^X2

^a3^X2

^b

L'étude du modèle a été réalisée en considérant les paramètres utilisés dans de nombreuses études antérieures (e.g. Gragnani et al. , 1998). Ces paramètres ont la particularité de faire l'hypothèse d'une chalne trophique sans perte d'énergie, c'est a dire avec e = 1, i ? {2, 3} (Tab. 1). Il a été démontré que cela n'affectait pas la dynamique générale du modèle (Abrams & Roth, 1994).