Résultats et discussion
4 Modèle de Rosenzweig MacArthur (R-M)
4.1 Dynamique en absence du superprédateur
Ce modèle comporte trois points d'équilibres
différents dont l'existence et la stabilité sont régies
par la valeur de K, qui peut s'interpréter comme la richesse du
milieu. Il s'agit donc du paramètre de
bifurcation5 naturel du système (Fig. 3). Tout
d'abord l'équilibre sans proies ni prédateurs dans le
système, E1 = (0, 0), existe quelque soit la valeur de
K. Il s'agit d'un point selle, stable selon l'axe des
prédateurs et instable selon l'axe des proies. Le second
équilibre qui correspond a l'établissement d'une certaine
quantité de proies mais sans maintien du prédateur,
E2 = (K, 0), existe toujours lui
aussi. Il est stable si K < X 1 et se comporte en
point selle sinon. Enfin, le troisième point
d'équilibre, E3 = (X 1,
X 2) (Eq. 3) n'existe que si K > X
1.
d2 b2
E3 = (X 1,
X 2) = ,
e2 a2 - d2
|
)
rX
(1 - K )(b2 + X
1 1)(3)
a2
|
|
E3 est stable si K < b2
+ 2X 1 ou occupe le centre instable d'un cycle
limite sinon. On remarque donc que l'enrichissement du milieu, c'est a
dire l'augmentation de K, provoque des fluctuations de la biomasse des
proies et des prédateurs par l'intermédiaire de l'apparition
d'un cycle limite. La dynamique du modèle se
décompose donc en trois phases selon l'augmentation de K :
Si K < X 1 , seule la proie se
maintient a la capacité limite du milieu (E2).
Si x 1 < K < b2
+ 2X 1 , un équilibre stable entre proies et
prédateurs est atteint dont la position est donnée par
l'équilibre E3 (Eq. 3).
Si K> b2 + 2X
1 , un cycle limite correspondant a des fluctuations
périodique apparait. Ces fluctuations sont amplifiées par
l'augmentation de K.
5Les mots en écriture penchée
sont définis dans l'annexe A

FIG. 3 - Valeurs de bifurcation du modèle R-M,
existence, stabilité et survie des deux espèces.
L'apparition de ces fluctuations d'effectifs pour des valeurs
de K élevées rend les biomasses parfois très
faibles ce qui augmente le risque d'extinction de la population de proie ou de
prédateur. La définition d'un seuil en dessous duquel
l'espèce est considérée comme éteinte permet de
rendre compte de la baisse de la richesse spécifique. Les domaines
d'extinction ou de persistance de la proie et de son prédateur en
fonction de K et de r peuvent ensuite être
considérés (voir section 6.2).
4.2 Dynamique en présence du
superprédateur
Le modèle R-M a trois équations (Eq. 1)
possède les trois points d'équilibres précédents
sans superprédateur et deux équilibres propres autorisant le
maintien du superprédateur (Eq. 4).
Ei = (X 1,i,
X 2,i, X 3,i)
())
(e 2 a2 X
1,i
= X 1,i, d3 b3
,b3 +
X 2,i - d2
e3 a3 - d3a3
b2 + X 1,i
( )
r 1 - X 1,i
oü X 1,i est la solution de
(b2 +X 1,i)= 0 pour i E
{4, 5}
a2 K
|
(4)
|
|
L'ajout du superprédateur fait apparaitre de nouvelles
dynamiques d'équilibre plus complexes pour la chalne trophique (Fig. 4).
En effet, lorsque les conditions sont favorables a son maintien, pour une
capacité limite du milieu suffisamment importante et pour un taux de
croissance assez élevé, quatre type de dynamiques
peuvent être observées : constante (A),
périodique basse fréquence (B), chaotique (C)
et périodique haute fréquence (D).
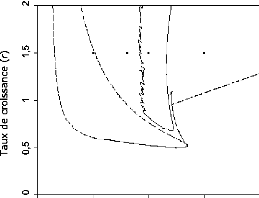
FIG. 4 - Différents régimes rencontrés a
l'état d'équilibre pour le modèle R-M en présence
du superprédateur. Les lettres A a D et les points associés
situent les valeurs des paramètres choisis pour réaliser
les portraits de phase présentés sur la figure suivante,
d'après Gragnani et al. (1998)
Une manière simple de visualiser ces dynamiques au
cours du temps (Annexe B) est d'en construire une représentation
graphique oü chaque axe représente la biomasse d'un échelon
trophique, une variable d'état différente du
système. Dans un tel graphique, chaque point correspond a un état
différent de la chalne trophique. Une trajectoire dans ce graphique rend
donc compte de l'évolution du système puisqu'elle parcourt la
succession de ses états au cours du temps. Comme il s'agit de
modèles pour lesquels chaque état différents n'admet qu'un
unique avenir, modèles dits déterministes, les trajectoires ne
pourront se croiser. Ces trajectoires dépendent en outre du point de
départ choisi, c'est a dire des valeurs des variables d'état
au départ de la simulation, appelées conditions
initiales. L'ensemble des trajectoires obtenues pour toutes les
conditions initiales forme le portrait de phase tandis que
l'ensemble des axes portant les variables constitue l'espace des
phases.
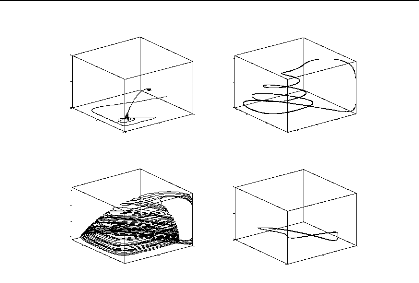
Les différents portraits de phases obtenus selon un
gradient d'enrichissement sur K et pour r = 1, 5 montrent la
succession de quatre types de dynamique (Fig. 5). Le premier (A) correspond a
l'attraction de la trajectoire vers un équilibre ponctuel
constitué par le point noir. La trajectoire du système
avant d'atteindre cet équilibre correspond au régime
transitoire. Ce régime transitoire a été
supprimé des repré-
10
10
0.3
1
1
0.5
X1
C
0.1 X2
0.20.4 0.6
X1
K = 1
1
0.6 0.40 .2
X2
0
0
X2
8
X3 7
6 2
K = 0,5 A K = 0,8
B
X3
5
X3
8
X2
0
0
X1
K = 1,5
D
1
1
2
6
0.5
0
2
12
X310
8
6
0.5
X1
FIG. 5 - Portraits de phase présentant
différentes dynamiques en présence du superprédateur. Ces
dynamiques sont rencontrées de (A) a (D) selon un gradient
d'enrichissement sur K pour r = 1, 5. (A) équilibre
ponctuel, (B) cycle limite basse fréquence, (C) attracteur
étrange et (D) cycle limite haute fréquence.
sentation suivante pour mieux mettre en évidence la
complexité des attracteurs qui rend compte du régime a
l'équilibre du système, dit régime asymptotique.
Le second (B) correspond a un cycle limite qui se traduit par des
oscillations lentes périodiques des biomasses des différentes
espèces. Le troisième portrait de phase (C) est la
représentation dans l'espace des phases d'une dynamique chaotique.
L'attracteur est alors nommé attracteur
étrange. Le dernier portrait de phase (D) est un cycle
limite qui se traduit par des oscillations périodiques
rapides des biomasses des différentes espèces. Cette
séquence pour ce même modèle peut être plus
compliquée ou plus simple selon la valeur des différents
paramètres. Des états transitoires entre ces
différentes dynamiques peuvent apparaltre comme la coexistence de deux
attracteurs entre le chaos et le cycle limite a
haute fréquence. La disparition de la dynamique chaotique est
aussi possible avec un superprédateur qui ressemble au prédateur
pour les paramètres de prédation et de croissance
(Abrams & Roth,
1994).
RéSULTATS ET DISCUSSION
| 


