Méthodes géostatistique pour l'interpolation et la modélisation en 2d/3d des données spatiales

Chapitre II : Méthodes de la géostatistique linéaire

La géostatistique se réfère aux méthodes d'analyse probabiliste pour étudier des phénomènes corrélés dans l'espace appelés phénomènes régionalisés. A ce titre elle fournit différents outils pour répondre au problème posé par la cartographie du socle rocheux dans le golfe du Morbihan.

1/ Notations et définitions

1.1/ Notion de variable régionalisée et notion de champ

Une variable régionalisée quantifie des grandeurs mesurées sur l'espace géographique. L'espace dans lequel cette variable prend ses valeurs est appelé champ.

Exemple de variable régionalisée : la profondeur du substratum sous le niveau zéro de la mer, mesurée par des campagnes sismiques dans une zone géographique située à l'est de l'île aux Moines, dans le golfe du Morbihan.

Exemple de champ : la zone géographique située entre la côte et l'est de l'île aux Moines. Nous pourrons estimer les valeurs prises par la variable régionalisée dans cette zone.

1.2/ Notations

Z : la variable régionalisée

D : le champ (domaine sur lequel la variable régionalisée est définie) s ? D : une position dans le champ

Z(s) : une valeur prise par la variable régionalisée au point s

Z à ( s ) : une estimation de Z(s)

h : la distance qui sépare deux points

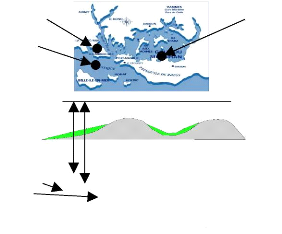
Z(s2)

Z(s3)

Z(s₁)

Niveau Zéro

Profondeur à estimer

Bathymétrie

Sédiments

Roche

14

Prenons un exemple dans le golfe du Morbihan

si est un l'emplacement géographique.

Tous les si ont une profondeur de roche : Z(si).

Chaque profondeur de roche est une variable aléatoire. Ensemble elles forment une fonction aléatoire de s.

La mesure faite au point si est une réalisation particulière de la fonction aléatoire Z(si).

Définissons à présent les hypothèses indispensables pour utiliser les techniques de la géostatistique linéaire.

2/ Hypothèses de base

Une fonction aléatoire {Z(s), s ? D} est caractérisé par sa loi spatiale F. Elle correspond à la loi de probabilité conjointe de (Z(s1), Z(s2), _Z(s3), ..., Z(s_n)).

F v v v P Z s v Z s v Z s v

( , ,..., ) ( ( ) ), ( ( ) ),..., ( ( ) )}

= { < < <

1 2 n 1 1 2 2 n n

Or cette fonction est très complexe par l'infinité des combinaisons possibles. Nous n'allons donc pas pouvoir estimer la fonction de distribution conjointe. La géostatistique linéaire se limite à la fonction de distribution d'ordre un F(v) et d'ordre deux FZ(si),Z(sj)(vi,vj) .

FZ (s ) ( v) = P{ Z (s ) = v}

F _i

( ) , ( ) ( , ) { ( ( ) ) , ( ( ) )}

=

Z s Z s i j

v v P Z s v Z s v

= =

i i j j

j

i ? j i=1,...,n et j=1,...,n

La première nous permet de calculer l'espérance de la fonction aléatoire Z en un point s.

E ( Z ( s )) = v
· fZ(s ) (v)dv

avec ( ) ' ( )

f Z ( s ) v = F Z ( s ) v

La fonction de distribution d'ordre deux, fourni la loi de probabilité entre les valeurs prises en deux sites si et sj. On utilise la covariance pour quantifier le degré de ressemblance entre les valeurs prises en si et sj et le variogramme pour mesurer la dissemblance entre les valeurs prises aux sites si et sj.

cov( s _i ,s ) = E(Z ( s _i ) Z ( s _j )) - E(Z ( s _i )) E ( Z (s j ))

ã( s _i , s _j ) = Var Z s _i Z s j

1 [ ( ), ( )] , (variogramme^*)

2

Le problème qui se pose est que la variable régionalisée est observée qu'une seule fois à un endroit précis. En d'autres termes, nous n'avons qu'une seule réalisation de la variable aléatoire. Or pour estimer les moments d'ordre un et deux il nous faudrait un grand nombre (>30) d'observations. Ce problème ne concerne pas la quantité d'information disponible mais le fait que l'on essaie de décrire un phénomène unique (profondeur au toit du socle rocheux), qui ne se répète pas, à l'aide de lois de probabilités.

Pour palier à ce problème nous posons comme hypothèse que la variable régionalisée est stationnaire. Concrètement cela veut dire que deux paires de points espacés d'un même vecteur h ont des caractéristiques (moyenne et covariance) semblables. Ou encore, la variable régionalisée ne dépend pas de sa position dans l'espace, elle garde les mêmes caractéristiques

* ã : cigle retenu pour désigner le variogramme

où que l'on se place. Cela nous permet de nous détacher de la localisation et de nous restreindre uniquement à la distance qui sépare les points d'observations.

La traduction mathématique est la suivante : Stationnarité du second ordre :

Une fonction aléatoire Z(s) est stationnaire du 2^nd ordre quand l'espérance mathématique existe et ne dépend pas du point s ; et que la covariance entre chaque paire ( Z(s+h) , Z(s)) existe et ne dépend que de h (distance).

- L'espérance mathématique ne dépend pas de s : ? s , E(Z ( s )) = m constante indépendante de s

- La covariance entre Z(s) et Z(s+h) ne dépend que de h :

? s s h

, + , cov ( ( ) , ( ) ) ( )

Z s h Z s C h

+ = ne dépend que de h et non de s

C(h) est appelé fonction de covariogramme

- La variance existe en tout site s et est une constante indépendante du site s :

? s Var ( Z s ) ( Z s Z s ) C cons te

, ( ) cov ( ), ( ) (0)

= = = tan

- Le covariogramme et le variogramme sont liés :

? s s h Var Z s h Z s

, + , ( ( ) ( ) ) / 2 ( ) (0) ( )

+ - = ã h C C h

= -

Remarque : L'hypothèse de stationnarité d'ordre deux ne peut être validé de manière rigoureuse et infaillible à l'aide d'un test statistique sur les données expérimentales (Arnaud et Emery, 2000 p.107).

L'hypothèse intrinsèque :

On dit _qu'une fonction aléatoire Z(s) est intrinsè_que _quand ses accroissements Z(s+h)-Z(s) sont stationnaires d'ordre 2. C'est-à-dire que

- L'espérance des écarts est zéro :

E ( Z ( s + h ) - Z(s )) = 0 ? s et h fixé

- La variance des écarts ne dépend que de h :

Var Z s h Z s E Z s h Z s

( ( ) ( )) [ ( ( ) ( ))² ] 2 ( )

+ - = + - = ã h

Cette hypothèse permet de dire que la variabilité entre les valeurs prises en deux points différents ne dépend que de h (la distance entre ces points).

Toute fonction aléatoire stationnaire d'ordre deux est également intrinsèque (la réciproque est
fausse). Autrement dit, l'hypothèse de stationnarité intrinsèque est moins restrictive que la

stationnarité du second ordre. L'hypothèse intrinsèque ne requiert pas de connaître l'espérance ni sa covariance de la variable aléatoire.

La fonction la plus utilisée en géostatistique pour décrire la continuité spatiale est le variogramme. La continuité spatiale est réalisée lorsque les valeurs prises entre deux sites proches l'un de l'autre sont similaires.