Utilisation des Machines à Vecteurs de Support (SVM) pour la reconnaissance des chiffres manuscrits

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE
Ministère de l'Enseignement Supérieur et de laRecherche Scientifique

Université des Sciences et de la Technologie Houari Boumediene

Faculté d'Electronique et Informatique

Département Instrumentation et Automatique

Mémoire de Projet de Fin d'Etudes d'Ingénieur d'Etat en Electronique

Option : Contrôle

THEME

Utilisation des Machines à Vecteurs de Support (SVM)
pour la reconnaissance des chiffres manuscrits.

Proposé et dirigé par : Présenté par :

Melle. NEMMOUR Hassiba Mr. DIBOUNE Rabah

Mr. CHIBANI Youcef Mr. FELLAH Hassen

Soutenu le Devant le jury com posé de :

Président :

Examinateur :

Promoteur :

Co-promoteur :

Promotion: 2006-2007

Remerciements

Nous remercions El laah de nous avoir donné la volonté et le courage qui nous ont permis de
réaliser ce travail, veuille t-il nous guider dans le droit chemin.

Nous aimons spécialement remercier Mlle H.NEMMOUR et Mr V. CHIBANI, qui nous ont
proposé ce suj et , pour leur grandes disponibilité pendant toute la durée de ce travail, pour
nous avoir toujours encouragé face à la difficulté , mais aussi pour leur gentillesse et leur
hospitalité.

Nous remercions aussi les membres de jury pour avoir accepter de juger notre travail.

Pour terminer, nous remercions toute personne ayant participé de prés ou de loin pour la
réalisation de ce travail.

Dédicaces

A mes très chers parents qui ont toujours été la pour moi, et qui m 'ont donné un magnifique
modèle de labeur et de persévérance et tout mon amour ;
A ma grand -mère khadudja qui a beaucoup sacrifie tout au long de ma vie, qu 'El laah la
pardonne
A mes oncles ;
A mes chers frères et soeurs : Mounir, Mehdi, Islam, Salim ;
A tous mes amis : Hichem, Djamel, Abd el hak , Mbarek, Abd el fattah, Mourad
,Soufianne,... ;
Je dédie ce mémoire

Rabah

A mes très chers parents qui ont toujours été la pour moi, et qui m 'ont donné un magnifique
modèle de labeur et de persévérance et tout mon amour ;
A ma grand -mère Haffssa qui a beaucoup sacrifie tout au long de ma vie, qu 'El laah la
pardonne
A mes oncles ;
A mes chers frères et soeurs : Mohamed, Kamel, Hossine, Salim ;
A tous mes amis : Hichem, Billel, Oualid , Ayman,Hamza , Mohamed ... ;
Je dédie ce mémoire

Tables des Matières

Introduction Générale 1
CHAPITRE 1

Reconnaissance des Chiffres Manuscrits

1. 1.Introduction ..3

1.2. System standard de reconnaissance des chiffres manuscrits ...4

1.2.1 Acquisition de l'image 5

1.2.2. Prétraitement ..5

1.2.2.1. Binarisation de l'image ...5

1.2.2.2. Elimination du bruit ......6

1.2.2.3. Segmentation des chiffres 6

1.2.2.4. Normalisation de l'image.. 6

1.2.3. Classification 7

1.2.4. Post-traitement: ...7

1.3. Méthodes de classification 7

1.3.1 Réseaux de neurones 8

1.3.2 Support Vecteur Machine (Machines à Vecteur de Support) 9

1.4. Conclusion 9

CHAPITRE 2

Machines a Vecteurs de Support

2.1. Introduction 10

2.2. Formulation mathématique des SVMs 10

2.2.1. Principe 10

2. 2.2. Données linéairement séparables .10

2.2.3. Données non linéairement séparable .13

2.2.3.1. Fonction noyau 15
2.2.3.2. Conditions de Mercer.........................................................................16

2.2.3.3. Exemples de noyaux	17
2.3. Implémentation multiclasse	..18
2. 3.1. Un contre tous (OAA : One Against All)	...18
2. 3.2. Un contre un (OAO : One Against One)	19
2.4. Méthode d'entrainement des SVMs	..19
2.4.1. Optimisation minimale et séquentielle SMO	....20
2.4.1.1. Fonctionnement de l'algorithme SMO	.21
2. 4.1.1.1. Optimisation analytique des multiplieurs du lagrangien	24
2. 4.1.1.2. Choix des multiplieurs du Lagrangien	...25
2.4.1.1.3. Mise à jour du seuil b	26
2. 4.1.1.4. Mise à jour de l'erreur	26
2.4.1.2. Pseudo code de l'algorithme SMO	..26
2.5. Conclusion	..30

Chapitre 3

Résultats Expérimentaux

3.1. Introduction	31
3.2. Critères d'évaluations	......31
3.1.1. Base de données USPS	.31
3.1.2. Matrice de confusion	.32
3.3. Apprentissage des SVMs	33
3.3.1. Réglage des paramètres	33
3.3.1.1. Paramètre de régularisation C	33
3.3.1.2 .Réglage des seuils de Tolérance et å	34
3.3.2. Choix du noyau	34
3.4. Classification binaire	34
3.4.1. Choix des pairs de classes	34
3.4.2. Evaluations	.34
3.4.3. Comparaison des résultats et discussions	37
3.5. Classification multi classe	..38

3.5.1. Evaluations 38
3.5.2. Comparaison des résultats et discussions .....................................................44

3.6. Comparaison classification binaire et multi-classe 3.7. Présentation de la plateforme	..47 .47
3.7.1. Fenêtre principale	47
3.7.2 Menu	48
3.7.2.1. Sélection des fichiers	48
3.7.2.2. Sélection des paramètres pour l 'apprentissage	49
3.7.2.3. Evaluation de la classification	.50

3.8. Conclusion 54

Conclusion Générale 55

Références Bibliographies ....A

Liste des figures et des tableaux

Figure 1.1 .Exemple des chiffres séparés	.4
Figure 1 .2.Exemple des chiffres touchés	...4
Figure 1.3.Diagrame des étapes principales de system de reconnaisance standard	5
Figure 1.4.Exemple de segmention des chiffres manuscrits	.6
Figure 1 .5.Exemple des chiffres manuscrits normalisées	6
Figure 1.6. Apprentissage supervisé d'une machine.	.8
Figure 2.1. Hyperplan de séparation linéaire pour des données linéairement séparables ...	11
Figure 2.2 .Hyperplan de séparation linéaire pour des données non linéairement séparables......	13

Figure 2.3.Exemple d'une application CP rendant les données linéairement séparables

15

Figure 2.4. Schéma synoptique de l'implémentation Un Contre Tous 19

Figure 2.5. Deux cas d'optimisations 21
Figure 2.6. Quand les deux multiplieurs sont égaux à la bande C : les vecteurs de support 2 et

r donnent le même seuil b. Les points 8 et _?fournissentè les seuils b1 et b2 respectivement. Les

points d'erreur et le seuil b se trouve entre b1 et b2 26

Figure 3.1.Représentation de la base USPS 31

Figure 3.2. Exemple d'une matrice de confusion .33
Figure 3.3.Taux de bonne reconnaissance(%) pour chaque classe pour différents valeurs du

paramètre du noyau RBF ...45
Figure 3.4.Taux de bonne reconnaissance(%) pour chaque classe pour différents valeurs du

paramètre du noyau Polynomial .45
Figure 3.5.Taux de bonne reconnaissance(%) pour chaque classe pour différents valeurs du

paramètre du noyau KMOD (a =6) 46
Figure 3.6.Taux de bonne reconnaissance(%) pour chaque classe pour différents valeurs du

paramètre du noyau Distance négative ..46

Figure 3.7. Fenêtre principale ...47
Figure 3.8. Rubriques de menu Fichier..48

Figure 3.9. Exemple de chargement de la base d'apprentissage 48

Figure 3.10. Rubriques de menu Apprentis sage ..49

Figure 3.11. Exemple de choix de noyau et les paramètres pour la classification multiclasse.....49 Figure 3.12. Exemple de choix de noyau et réglage des paramètres avec possibilité de sélectionner

deux classes pour la classification biclasse ..50

Figure 3.13. Rubriques de menu Test 51

Figure 3.14.Matrice de confusion avec précision globale ...51
Figure 3.15. Taux de bonne reconnaissance pour chaque classe représenté sous forme

graphique 52
Figure 3.16. Taux de bonne reconnaissance pour déférentes classes représenté sous forme d'une

matrice de confusion et graphique. 53

Figure 3.17.Résumé des résultats ...54

Tableau 2.1. Exemples de noyaux 17
Tableau 3.1. Échantillon représentant la première dizaine d'images binarisées et leurs étiquettes

dans la base de données USPS 32

Tableau 3.2.Matrices de confusion pour les paires de classes (9 ,4) pour chaque type de noyau 35
Tableau 3.3.Matrices de confusion pour les paires de classes (5 ,6) pour chaque type

de noyau 36
Tableau 3.4.Matrices de confusion pour les paires de classes (7 ,1) pour chaque type de noyau .37

Tableau 3.5.Taux global de bonne reconnaissance pour les trois paires de classes (9,4), (7,1) et (5,6) .37

Tableau 3.6.Matrice de confusion de la classification multi classe pour le noyau RBF (ó =3)... .38

Tableau 3.7.Matrice de confusion de la classification multi classe le noyau RBF (ó =10) 39

Tableau 3.8.Matrice de confusion de la classification multi classe le noyau RBF (ó =25) 39

Tableau 3.9.Matrice de confusion de la classification multi classe pour le noyau Polynomial (p=1) 40
Tableau 3.10.Matrice de confusion de la classification multi classe pour le noyau Polynomial

(p=2) 40
Tableau 3.11 .Matrice de confusion de la classification multi classe pour le noyau Polynomial

(p=3) 41
Tableau 3.12.Matrice de confusion de la classification multi classe pour le noyau KMOD ã =0.2

et ó=6 41

Tableau 3.13.Matrice de confusion de la classification multi classe pour le noyau KMOD ã =0.5

et ó=6 .......................................................................................................................42 Tableau 3. 14.Matrice de confusion de la classification multi classe pour le noyau Distance négative ã =0.2 42

Tableau 3.15.Matrice de confusion de la classification multi classe pour le noyau Distance négative ã=0.1 43

Tableau 3.16.Matrice de confusion de la classification multi classe pour le noyau Distance négative ã=0.05 43

Tableau 3.1 7.Résumé des résultats pour la classification multi classe .........44

Introduction générale

Depuis plusieurs années, de nombreux travaux de recherche ont porté sur la reconnaissance des chiffres manuscrits. Deux grandes classes d'application sont aujourd'hui à l'étude : les applications bancaires ou postales, qualifiés de hors lignes ou statiques par exemple en France, deux millions de chèques sont lus chaque jour sans intervention humaine et les applications destinés à la bureautique, qualifiés de en lignes ou dynamiques ou temps réel (voir [8] et respectivement [4] pour des exemples).

Dans ce mémoire, nous nous intéressons à la reconnaissance des chiffres manuscrits hors - ligne qui reste aujourd'hui un thème de recherche ouvert. En effet, bien que le nombre de classes naturelles soit très réduit (chiffres '0' à '9'), on trouve à l'intérieur de chacune d'entre elles, une très grande variabilité de l'écriture, de plus, les conditions souvent relativement précaires dans les quelles sont écrits les chiffres (chèques écrits rapidement sur un coin de table) et la variabilité du matériel utilisé (utilisation de divers stylos, de différentes qualités de papier) tendent à complexifier la reconnaissance.

Plusieurs générations de machines d'apprentissage ont vu le jour dans le but de classifier, de catégoriser ou de prédire des structures particulières dans les données. Mais la plupart de ces techniques éprouvent de grandes difficultés à traiter les données de très haute dimension. Pour surmonter ce problème, on procède souvent par la sélection d'une partie des attributs des données pour réduire la dimension de l'espace d'entrée. Mais dans ce cas on aura besoin d'utiliser des hypothèses simplificatrices qui ne se vérifient pas toujours en pratique. Par ailleurs, une méthode issue récemment d'une formulation de la théorie de l'apprentissage statistique due en grande partie à l'ouvrage de Vapnik en 1995 intitulé the nature of learning statistical theory [27] surmonte ce problème en imposant que le nombre de paramètres soit linéairement lié au nombre des données d'apprentissage. Cette technique est appelée Support Vector Machines (SVM) ou machines à vecteurs de support. Bien que récemment proposée, elle a fait l'objet d'un nombre important de publications.

Le SVM est un modèle discriminant qui tente de minimiser les erreurs d'apprentissage tout en maximisant la marge séparant les données des classes. La maximisation de la marge est une méthode de régularisation qui réduit la complexité du classifieur.

De nombreux travaux ont démontré la supériorité du SVM sur les méthodes discriminantes classiques. Sa robustesse vis-à-vis de la dimensionnalité des données et son pouvoir accru de

généralisation, font que le SVM est nettement plus avantageux [20]. Le succès de cette méthode est justifié par les solides bases théoriques qui la soutiennent.

L'objet de ce mémoire est l'implémentations des SVMs pour la reconnaissance des chiffres manuscrits . Il est organisé en trois chapitres. Le premier chapitre présente les différents blocs, schéma standard de reconnaissance des chiffres manuscrits en mettant l'accent plus précisément sur le bloc classifieur.

Le deuxième chapitre décrit en détail le concept ainsi que la formulation mathématique des SVMs. Pour résoudre le problème d'optimisation des SVMs, une description détaillée de l'algorithme SMO est également présentée dans ce chapitre.

Le troisième chapitre décrit les différentes expériences réalisées sur une base de données de chiffres manuscrits. Les expériences sont réalisées pour une classification binaire puis multiclasse sans oublier l'interface que nous avons développée sous environnement Windows avec le logiciel matlab 6.5 et qui porte le nom « RCSVM ».

Dans la conclusion, nous rappelons l'objectif ainsi que les perspectives de ce travail.

Reconnaissance des Chiffres

Manuscrits

1. 1.Introduction

Durant les vingt cinq dernières années, la lecture optique et la reconnaissance d'écriture manuscrite ont été des domaines de recherches actifs et ont fait l'objet de nombreuses publications. [11] [14] [28] [26] [22] [17] [19] [3] [6]. En effet, le problème de la reconnaissance de caractères manuscrits n'est pas encore parfaitement résolu bien que l'on sache atteindre des taux de reconnaissance supérieure à 90% dans diverses applications, telle que la reconnaissance des 10 chiffres manuscrits. Dans ce sujet de reconnaissance, deux grandes classes de systèmes sont aujourd'hui à l'étude

- Les systèmes pour les applications bancaires ou postales, qualifiés de hors-ligne ou statique. Dans ce cas, il s'agit de réaliser un système pour lire le montant d'un chèque ou pour lire une adresse postale sur une enveloppe, les informations transmises au système seront les pixels d'une image acquise à l'aide d'un scanner.

- Les systèmes destinés à la bureautique, qualifiés de en ligne ou dynamique ou temps réel. Dans ce cas, il s'agit de saisir un texte avec un stylo et une table à digitaliser pour le transmettre à un traitement de texte, les informations se présenteront sous forme d'une suite de points arrivant dans un ordre bien déterminé, information qui sera importante pour la classification [25]. Dans le domaine de reconnaissance, il faut faire une nette distinction entre texte imprimé ou dactylographié et texte manuscrit. Si dans le premier cas, on peut considérer que les principales difficultés ont été surmontées, la situation est entièrement différente en ce qui concerne la reconnaissance d'un manuscrit que nous présenterons dans ce présent chapitre pour le cas des chiffres, où les difficultés resteront celles de la variabilité de l'écriture [9]. Ces variations dépendent en général aussi bien du scripteur que de l'environnement de l'écriture. En effet, la variabilité mett ant en jeu le scripteur peut provenir de l'inclinaison des caractères, de l'inclinaison de la ligne de base des chiffres vue que des différents directions de ligne peuvent coexister sur une même page du fait de changements d'orientation de la feuille en cours d'écriture, etc. [16]. La variabilité liée à l'environnement d'écriture correspond par exemple à la variation de l'épaisseur des traits en fonction du type de stylo utilisé et du support d'écriture disponible, ou à la présence plus ou moins importante de discontinuités [2].

Dans notre mémoire, nous intéressons au problème de reconnaissance d'écriture manuscrite hors-ligne, qui demeure un problème difficile car l'entrée de ces systèmes est une image. D'autres problèmes doivent également surmontés comme par exemple, comment on peut enlever le bruit comme des éléments du fond d'image, comment on peut traiter le manque des

traits etc. De plus, il n'y a pas d'information supplémentaire comme le cas d'en-ligne. D'ailleurs, pour être utilisés largement, ces systèmes doivent traiter rapidement avec le taux de reconnaissance élevé.

Par contre dans le cas de reconnaissance en ligne l'utilisateur écrit sur une table spéciale, il y a moins de bruit. De plus, on peut déterminer comment un caractère est écrit, c'est à dire, l'ordre de traits constituants ce caractère. D'ailleurs, la contrainte du temps de reconnaissance n'est pas stricte, on peut utiliser des algorithmes complexes. C'est pour quoi le taux de reconnaissance de ces systèmes est assez élevé. [18]

Il faut distinguer deux types d'écriture manuscrite hors-ligne. Dans le premier cas, chaque chiffre est séparé par l'utilisateur. Par exemple, chaque chiffre est écrit dans une boîte comme dans la figure suivante :

Figure 1.1 .Exemple des chiffres séparés.

Ce problème est bien résolu. Les algorithmes utilisés sont souvent des SVM (Support Vector Machine), réseau de neurones etc. [18]

Figure 1 .2.Exemple des chiffres touchés.

Dans le deuxième cas, les chiffres sont écrits normalement, c'est à dire, les chiffres se sont touchés. C'est à notre système de séparer ces caractères. Le problème devient plus difficile. Dorénavant, quand on parle d'écriture manuscrite, on aborde le deuxième cas.

1.2. System standard de reconnaissance des chiffres manuscrits

Le diagramme suivant montre les étapes principales du processus de reconnaissance d'écriture manuscrit hors-ligne.

Image Classe

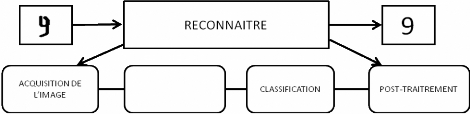
PRE-TRAITE M ENT

Figure 1.3. System standard de reconnaisance des chiffres manuscrits.

La démarche classique suivie en reconnaissance de chiffres manuscrits consiste à opérer selon les étapes suivantes :

1.2.1 Acquisition de l'image

L'écriture est digitalisée par un scanner pour être transformer en une image. Ceci correspond à l'entrée du système. Cette étape est assez simple mais très importante car elle influence sérieusement les étapes suivantes. Deux paramètres importants doivent être

pris en compte :

· Résolution : la résolution normale est de 300 dpi (dot per inch : points par pouce). Cependant, dans certains cas, lorsque la taille de l'écriture est petite, il est nécessaire d'augmenter la résolution pour tenir compte de la finesse de l'écriture.

· Niveau d'éclairage : l'éclairage influe également sur la qualité de la reconnaissance. Trop faible, le bruit devient important .Trop fort, le bruit est réduit mais les traits fins disparaissent.

1.2.2. Prétraitement

Cette étape prépare l'image entrée pour l'étape de reconnaissance. Elle essaie d'effacer les informations indésirables comme le bruit. Les opérations typiques regroupent la binarisation, élimination du bruit, segmentation en chiffres isolés, normalisation et squelettisation.

1.2.2.1. Binarisation de l'image

L'image entrée est représentée en niveau de gris et les algorithmes de reconnaissance courants travaillent souvent sur des images binaires. Donc, il faut appliquer un seuillage. Cependant, quand le fond est très compliqué, cela devient un problème difficile au cas où l'éclairage varie dans l'image entrée, on peut appliquer des techniques comme seuillage adaptatif [18].

1.2.2.2. Elimination du bruit

Le problème du bruit est très important mais très difficile particulièrement dans le cas où l'utilisateur écrit sur une feuille ayant le fond complexe comme un chèque de banque. Une technique simple est de faire la soustraction entre l'image entrée et l'image d'un chèque blanc (Il n'y a pas d'écriture). Cependant, les deux images doivent être alignées et les parties d'écriture qui traversent les éléments du fond vont être enlevées. La reconnaissance d'écriture sur un chèque de banque reste encore un défi [18].

.

1.2.2.3. Segmentation des chiffres

La segmentation consiste à séparer les chiffres les uns des autres. La difficulté de cette étape réside dans le fait que les chiffres ne sont pas alignés et ne présentent pas la même taille, de plus, dans certains cas, les chiffres se chevauchent. Par conséquents, il faut utiliser des techniques de séparation permettant d'isoler les chiffres [23].

Figure 1 .4.Exemple de segmention des chiffres manuscrits

1.2.2.4. Normalisation de l'image

Pour faciliter l'étape de reconnaissance, les chiffres segmentés doivent être normalisées à une taille fixée. La contrainte principale réside dans le choix de cette taille. Trop petite, il y a un risque d'une perte d'information. Trop grande, l'étape de reconnaissance va opérer lentement.

Figure 1 .5.Exemple des chiffres manuscrits normalisées

1.2.3. Classification

La classification consiste à affecter une forme donnée à une classe prédéfinie. Cette phase regroupe les deux taches d'apprentissage et de décision. En effet, à partir de la même description de la forme en paramètres, elles tentent, toutes les deux d'attribuer cette forme à un modèle de référence. Le résultat de l'apprentissage est soit la réorganisation ou le renforcement des modèles existants en tenant compte de l'apport de la nouvelle forme soit la création d'un nouveau modèle de l'apprentissage. Le résultat de la décision est un « avis » sur l'appartenance ou non de la forme aux modèles de l'apprentissage. [1] [24]

1.2.4 Post-traitement

Le post-traitement permet la validation des décisions de l'analyse sur la base de connaissances (du domaine). Cette étape aide à réduire considérablement des erreurs. Cependant, ce n'est pas une étape complètement séparée des étapes précédentes. [7]

1.3. Méthodes de classification

Généralement, un système de reconnaissance est construit à partir des connaissances a priori sur le problème. Le fait de classer un objet correspond donc à prendre une décision sur base d'une ou plusieurs règles. Dès lors, une des premières approches pour automatiser le traitement, fut d'extraire la connaissance experte de spécialistes sous forme de règles. Ainsi, pour chaque catégorie, on disposait d'un ensemble de règles permett ant de déterminer l'appartenance d'un objet à la-dite catégorie (ou classe). Bien que cette façon ait été largement utilisée jusqu'à la fin des années 80, on en conçoit aisément les limites. En effet, quand le nombre d'exemples et de classes est très important, il devient difficile de rassembler toutes les connaissances expertes nécessaires aux prises de décision. Dans les années 90, l'approche Machine Learning (ML) ou apprentissage machine devient très populaire. Il s'agit d'apprendre automatiquement les règles de décision sur base d'un ensemble d'exemples déjà classés.

L'apprentissage machine inclut entre autres les méthodes supervisées et non supervisées.

Dans les techniques non-supervisées, les objets sont présentés sans leur catégorie. Un exemple type de méthodes non-supervisées est le clustering dont le but est de créer des groupes (clusters) d'objets présentant des caractéristiques semblables.

Dans le cas des méthodes supervisées, on cherche à estimer une fonction f(x) à partir des exemples x, comme l'indique la figure ci-dessous. [15]

x,y = f(x)

Machine

f^~(x)

x,y = f(x) : Une donnée et son étiquette
f^~(x) est une estimation de f(x)

Figure 1.6. Apprentis sage supervisé d'une machine.

Parmi les méthodes qui ont été développées dans ce contexte (machine d'apprentissage), nous distinguons par exemple les réseaux de neurones et les machines à vecteurs du support (SVM : Support Vector Machines, en anglais).

1.3.1. Réseaux de neurones :

Un réseau de neurones est un assemblage de neurones connectés entre eux. Un réseau réalise une ou plusieurs fonctions algébriques de ses entrées, par composition des fonctions réalisées par chacun des neurones. La capacité de traitement de ce réseau est stockée sous forme de poids d'interconnexions obtenus par un processus d'apprentissage à partir d'un ensemble d'exemples d'apprentissage

Il arrive souvent que les exemples de la base d'apprentissage comportent des valeurs approximatives ou bruitées. Si on oblige le réseau à répondre de façon quasi parfaite relativement à ces exemples, on peut obtenir un réseau qui est biaisé par des valeurs erronées. Par exemple, imaginons qu'on présente au réseau des couples situés sur une droite

d'équation , mais bruités de sorte que les points ne soient pas exactement sur la

droite. S'il y a un bon apprentissage, le réseau répond ax+b pour toute valeur de x présentée. S'il y a surapprentissage, le réseau répond un peu plus que ou un peu moins, car

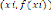
chaque couple positionné en dehors de la droite va influencer la décision. [10]

1.3.2. Support Vecteur Machine (Machines à Vecteur de Support) :

Les réseaux de neurones éprouvent de grandes difficultés à traiter les données de très haute dimension, de plus, ils possèdent un grand nombre de paramètres d'apprentissage à fixer par l'utilisateur. Pour surmonter ce problème, on procède souvent par la sélection d'une partie des attributs des données pour réduire la dimension de l'espace d'entrée. Mais dans ce cas, on aura besoin d'utiliser des hypothèses simplificatrices qui ne se vérifient pas touj ours en pratique. Par ailleurs, une méthode issue récemment d'une formulation de la théorie de l'apprentissage statistique due en grande partie à l'ouvrage de Vapnik en 1995 intitulé the nature of learning theory [27] surmonte ce problème en imposant que le nombre de paramètres soit linéairement lié au nombre des données d'apprentissage. Cette technique est appelée Support Vector Machines (SVM) ou machines à vecteurs de support. L'avantage principale provient du fait qu'il ya peu de paramètres à régler comparativement aux réseaux de neurones. Elle laisse très peu de place aux paramètres utilisateurs, bien que récemment proposée elle a fait l'objet d'un nombre important de publications.

1.4. Conclusion :

Dans ce chapitre, nous avons présenté les différentes étapes de reconnaissance des chiffres manuscrits hors-ligne et les méthodes de classification fondés sur les machines d'apprentissage.

Dans le système de reconnaissance, nous nous intéressons plus précisément au classifieur fondé sur les SVMs .Aussi, nous abordons dans le prochain chapitre la description détaillée de cette méthode de classification appliquées à la reconnaissance des chiffres manuscrits. Cette technique est appelé machines à vecteurs de support (SVM) qui appliquée avec une efficacité remarquable à la reconnaissance des chiffres manuscrits, au traitement d'images, à la prédiction de séries temporelles, au diagnostic médical, au contrôle qualité, etc. Des exemples d'application réussie des SVM peuvent être consultés sur Internet [12].

.

Machines à Vecteurs de

Support

2.1. Introduction

Le classfieur SVMs a été conçu pour une séparation de deux ensembles de donnée. Il est considéré donc comme un classfieur binaire.

Le but de SVM est de trouver un hyperplan qui va séparer et maximiser la marge de séparation entre deux classes. Le problème de recherche de l'hyperplan séparateur possède une formulation duale. Ceci est particulièrement intéressant car, sous cette formulation duale, le problème peut être résolu au moyen de méthode d'optimisation quadratique.

Différents algorithmes d'optimisation ont été développés parmi eux l'algorithme SMO (optimisation minimale et séquentielle) qui est un algorithme rapide proposé par platt [21] pour résoudre le problème de programmation quadratique des SVMs.

2.2. Formulation mathématique des SVMs

2.2.1. Principe

La tâche, qu'un classifieur doit effectuer, est exprimée par une fonction appelée fonction de décision reliant les exemples à classifier x (appelés espace d'entrée) à leur classes y (appelées espace de sortie). y correspond souvent à {- 1, + 1}.

Soit: {,? Ë}, : " ? {#177; 1}

f_á á f_á R l'ensemble de fonctions tel que (1, ₁ ),,(, )?"× {#177; 1}

xyKxlyl R

sont des exemples d'apprentissage indépendants générés aléatoirement selon une distribution de probabilité P(x,y) inconnue. Dans notre cas, la machine est supposée déterministe pour un x donné et un á donné, on obtient toujours la même sortie f(x, á). Un choix particulier de á génère ce que l'on va appeler «machine entraînée».

L'objectif des SVMs est de trouver un hyperplan permettant de séparer les données d'apprentissage de sorte que tous les points d'une même classe soient d'un même coté de l'hyperplan. Deux cas peuvent se présentent :

· Données linéairement séparables.

· Données non linéairement séparables.

2.2.2. Données linéairement séparables

On définit l'ensemble de données d'apprentissage par :

{}{}" xyilyxR

,, =1,K,,?-1,+1,?

i i i i

En supposant que nous disposons d'un hyperplan séparant les données positives des données négatives, les x_i qui appartiennent à l'hyperplan vérifient la relation :

. x_i·w+b=0 (2.1)
w est la normale de l'hyperplan et b paramètre de l'hyperplan (seuil).

Pour le cas linéairement séparable, l'algorithme de vecteurs de support cherche simplement l'hyperplan séparateur permettant la plus large marge. Ceci est formulé par :

x_i · w+b=+1 poury_i=+1 (2.2)

x_i·w+b=-1 poury_i=-1 (2.3)

Ces équations peuvent être combinées dans l'inégalité suivante :

yi(x _i ·w+b)=1;?i (2.4)

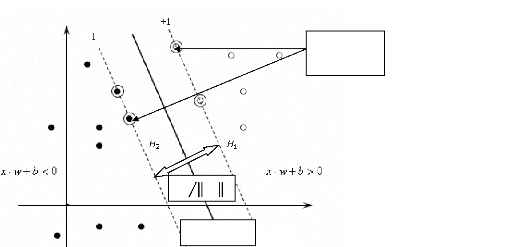
Vecteurs de support

: Données représentes des classes

2

w

x_i

.w+b

0

Figure 2.1. Hyperplan de séparation linéaire pour des données linéairement séparables.

Les points vérifiant l'égalité de (2.2), appartiennent à un hyperplan H1 :

x_i·w+b=+1 (2.5)

Similairement, les points vérifiant l'égalité de (2.3), appartiennent à l'hyperplan H2 :

x_i ·w+b=-1 (2.6)

(comme indiqué par la figure :2.1)

L'hyperplan optimal est celui pour lequel la distance aux points les plus proches (marge) est maximale. Cette distance vaut 2 w .

Maximiser la marge revient donc à minimiser 2

wde l'inégalité (2.4). Pour cela, le problème est reformulé sous forme de Lagrangien. Il y a deux raisons pour cela. La première est que la contrainte dans (2.4) sera remplacée par une contrainte sur les multiplieurs du Lagrangien qui sera plus facile à

traiter. En plus, dans cette reformulation du problème, seules les données d'apprentissage apparaissent sous forme de produit scalaire. Ainsi, on introduit des multiplieurs ái positifs, i = 1,K , l dans (2.4). Les contraintes dans (2.4) sont multipliées par les á_i et sont ensuite

soustraites de 2

1 w pour former le Lagrangien.

2

l l

á (2.7)

i

1 2

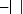
L w y x w b

= - · + +

? = ( ) ? =

á

p i i i

2 i 1 1

i

¹

L= ? á- ?

D i ²ⁱj

(2.10)

i

,

áá ·

i j i j i j

y y x x

Lp est appelé lagrangien primal.

On doit minimiser le Lagrangien par rapport à w et simultanément exiger que ses dérivées par rapport à tous les multiplieurs du Lagrangien á_i disparaissent. Une autre contrainte impose que

?i, á_i = 0. En imposant que les gradients de Lp par rapport à w et b disparaissent on obtient :

Vs

w ?

=á

i yx (2.8)

i i

i=1

?_i =0

^ái^yi (2.9)

Vs : Nombre de vecteurs de support.

En substituant les équations (2.8) et (2.9) dans (2.7) nous obtenons :

LD: est appelé lagrangien dual.

Les points dont les ái sont strictement supérieurs à 0 sont appelées vecteurs de support et appartiennent à l'un des hyperplans H1 ou H2. Ces points sont les plus proches de la frontière de décision et forment le plan séparateur.

2.2.3. Données non linéairement séparables

Lorsque les exemples ne sont pas linéairement, séparables les contraintes (2.2) et (2.3) sont relâchées en introduisant des variables d'écart îi ? 0, i =1, ....., l

qui deviennent : x _i ·w+b=1-î _i poury _i = +1 (2.11)

xwb î pour y (2.12)

_i· += -1+_{i i}= -1

î _i =0 ?i (2.13)
Pour qu'une erreur se produise, le î_i correspondant doit être supérieur à 1.

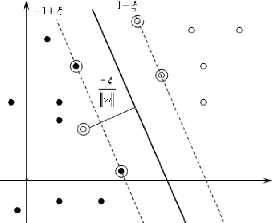
Figure 2.2. Hyperplan de séparation linéaire pour des données non linéairement séparables

Maximiser la marge revient donc à minimiser + ? 2 w /2C i

î i . (2.14)

C :est un paramètre choisi par l'utilisateur, plus qu'il est grand plus la pénalité sur l'erreur est grande.

La formulation lagrangienne devient :

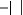
i i

^{1 2}

L wC

P i

= +- i

2

? ? ?

î áîâî

{()}_i

yxwb1(2.15)

iii

· +-+-_i

i

Les â_i sont des multiplieurs du Lagrangien introduits pour forcer la positivité des î_i. Le Lagrangien doit être minimisé par rapport à w, b,î et maximisé par rapport à á etâ.

? Lp ? w

0

w = ? á _i yx (2.16)

i i

i

= 0(2.17)

? ? i

L á

p y

=- i

? b i

? L_p

0

? b

C-á_i-â_i=0 (2.18)

?Lp =

î i

?

0

Ce qui induit à un problème dual :

(2.19)

Maximiser : Lyyxx

= ? á- ?áá·

¹

D i ijijij

i

i , j

2

Sous contrainte que :

0=á_i=C (2.20)

l

et ?i⁼⁰

á_iy (2.21)

i

=

w

V S

?=

i 1

La solution est donnée encore par :

á (2.22)

i^yi^xi

VS est le nombre de vecteurs de support

Dans le cas où 0< á_i <C , nous avons î_i = 0 ce qui nous permettra de déterminer le seuil b après l'optimisation. En effet, une fois w et b sont déterminés la fonction de décision est donnée par

? ?+> fxi () á = ? ?=+ Vs fxisign iyixixb1 si ()0 T ? ?x i fx ? 1 si () 0 ? ? i1 ? ? - < i

(2.23)

Les vecteurs de support aident à bien définir la surface de décision car ces exemples utilisés dans le calcul de cette fonction de décision.

2.2.3.1. Fonctions noyaux

Dans la plupart des cas les données à classer ne sont pas linéairement séparables. Tandis que les SVMs sont conçus pour séparer linéairement les données. L'idée des SVMs est de changer l'espace des données. Cette transformation conduit à un changement de dimension des données d'entrée. Par conséquent, il devient donc possible d'envisager d'utiliser la méthode des SVMs.

Dans le problème d'apprentissage, les données apparaissent sous forme de produit scalaire x_i · x_j.

Supposons que nous avons tracé ces données dans un autre hyperplan .7{ (.7{ étant un espace euclidien dont la dimension peut être infinie) en utilisant une application Ö telle que :

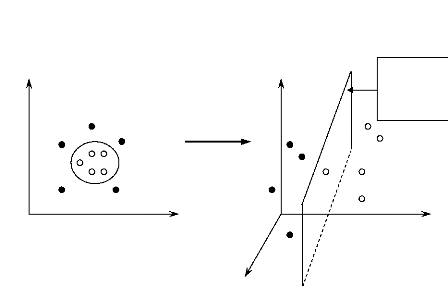
x1

R

^d?.7{

Ö :

Hyperplan
de
séparation

x2

x1

x2

Ö

x3

Figure 2.3. Exemple d'une application Ö rendant les données linéairement séparables

Alors l'algorithme d'apprentis sage va dépendre des données au travers des produits scalaires dans l'espace H des fonctions de la formeÖ(x _i )·Ö(x_j). Cet espace est appelé espace de traits ou feature

space. Il est difficile de travailler explicitement avec Ö. Dans ce cas, une fonction K appelé noyau ou Kernel définie par Ê(x_i ,x_j ) = Ö(x _i )· Ö (x_j). Ainsi, il suffit de définir uniquement le noyau K

sans connaissance explicite de Ö. En remplaçant x_i · x_j par K(x_i ,x_j) partout, nous obtenons une
machine à vecteurs de support fonctionnant dans un espace de dimension infinie. Toutes les considérations décrites précédemment seront vérifiées puisque nous maintenons touj ours la séparation linéaire, mais dans un espace différent.

2.2.3.2. Conditions de Mercer [15]

La fonction noyau ou Kernel évite la connaissance explicite de Ö et permet ainsi de connaître la similarité entre deux exemples. La matrice contenant les similarités entre tous les exemples d'une base d'apprentissage K est appelée matrice de Gram.

? KKK 11 12 1 L l ? ? ? ? KKK 21 222 L l ? K=? ? M M O ? ? ? KKK llll L 1 2 ?

(2.24)

Cependant, pour qu'une fonction K : X× X ?R corresponde au produit scalaire dans l'espace de traits, elle doit répondre à des conditions dite de Mercer.

· Théorème

La fonction K(x_i ,x_j): X× X ? R est un Kernel si et seulement si :

K=(K(x _i ,x _j )/i,j=1, l) (2.25)

est définie positive.

Notons qu'une fonction X× X ? R générant une matrice définie positive possède les trois propriétés fondamentales du produit scalaire : ?x _i ,x_j ? X

1. Positivité : ^K(xi ,x_j ) = 0 (2.26)

2. Symétrie : K(x_i,x_j)=K(x_j,x_i) (2.27)

3. Inégalité de Cauchy-Shwartz : K(x _i ,x_j) = xi·x _j (2.28)

La condition de Mercer nous indique si une fonction est un noyau mais nous n'avons aucun renseignement sur l'application Ö (et donc sur l'espace de traits) induit par ce noyau. Dans le reste de cette section, nous présentons quelques noyaux utilisés dans différentes applications de reconnaissance de formes.

2.2.3.3. Exemples de noyaux

Nous présentons dans le tableau les noyaux utilisées dans ce mémoire pour la reconnaissance des chiffres manuscrits.

Noyau	K(x i ,x j )			Paramètres
RBF (Radial Basis Function)	2 ? - ? ? x i x j ?			ó: est un paramètre qui permet de régler la largeur de la gaussienne.
	expó?^-2 ? 2 ? ?
Polynomial	( )^pp x i , x j +1			: est l'ordre du polynôme.
Distance négative	( ) ãã -x i - x j			: Paramètre du noyau régler dans ]0,2].
KMOD: (de l'anglais «Kernel with Moderate Decreasing»)	? ? ? 2 ?? ã ??A: A	- ^1	? ?	??normalisation. est une constant de ? et : contrôlent ó l'écrasement du noyau.
	??exp2 ? 2 ? -+ó ^xi^xj ? ? ? Avec : 1 A=
	ã 2 ?? - exp1^??
	2 ? ó ?

Tableau 2.1. Exemples de noyaux

M

(2.33)

arg max

)

f

1

(x_i

i=

Il est possible de composer de nouveaux noyaux en utilisant des noyaux existants. Si K₁(·,·), K₂(·,·) sont des fonctions satisfaisant les conditions de Mercer, et étant donnés +

a?R et B une matrice

définie positive, alors les fonctions suivantes sont des noyaux :

1. (ij)(ij)(ij) KxxKxxKxx

,=₁,+₂, (2.29)

2. K(x_i,x_j)=aK₁(x_i,x_j) (2.30)

3. K(x_i x_j ) K(x_i x_j )K(x_i x_j)

,= 1 ,₂ , (2.31)

4. ()_j

Kx_i,x_j=x_iÂx (2.32)

T

2.3. Implémentation multi-classe

A l'origine, les SVMs ont été conçus essentiellement pour la séparation de 2 classes. Cependant, plusieurs approches permettent d'étendre cet algorithme aux cas de plusieurs classes [5].

2.3.1. Un Contre Tous (OAA : One Against All)

Pour chaque classe, on détermine un hyperplan séparant celle-ci de toutes les autres classes. Ainsi, pour M classes, on doit déterminer M fonctions de décision.

Tous les exemples appartenant à la classe considérée sont étiquetés positivement (+1) et tous les exemples n'appartenant pas à la classe sont étiquetés négativement (-1).

La figure 2.4. décrit le schéma synoptique de principe pour la séparation multi-classe.

Ainsi, pour chaque exemple de test, M valeurs de sortie f_i (x)avec (i=1,... M) sont disponibles.

Ainsi, une donnée est affectée à la classe qui correspond à la valeur maximale des fonctions de décision :

Classe 1

SVM1

.

Autres classes

Affectation à la classe

Forme x

.

.

.

Classe M

SVMM

Autres classes

Figure 2.4. Schéma synoptique de l'implémentation Un Contre Tous

2.3.2 Un contre un (OAO : One Against One)

La deuxième méthode, est une méthode dite de Un Contre Un. Au lieu d'apprendre M fonctions de décisions, ici chaque classe est discriminée d'une autre. Ainsi M (M-1 )/2 fonctions de décisions sont apprises et chacune d'entre elles effectue un vote pour l'affectation d'un nouveau point x. La classe de ce point x devient ensuite la classe majoritaire après le vote.

2.4. Méthode d'entraînement des SVMs [21]

Le calcul de la solution d'un SVM consiste à résoudre le problème de programmation quadratique qui est un problème d'optimisation formulé comme suit :

l ll

() ( ) i j

1 max(2.34)

i j i j

,

á ?== ?? =

L y y K x x

Di

^áá á á

= -
i1 1 1

2 ij

Sous contrainte que :

0=á_i = C,?i (2.35)

(2.36)

l

et 0

?=

á _i y i

i =

1

Le problème de programmation quadratique (PQ) provenant d'une SVM ne peut pas être facilement résolu avec les techniques standards. La matrice de gram contient un nombre d'éléments égal au carré du nombre total des données de la base d'apprentissage. Pour résoudre ce problème, Un algorithme appelé Sequential Minimal Optimisation SMO ou Optimisation minimale et séquentielle, a été proposé pour accélérer l'apprentissage d'un SVM [21].

L'optimisation de ce problème se termine lorsque tous les exemples de la base d'apprentissage obéissent aux conditions Karush-Kuhn-Tucker (KKT) [21] suivant :

()^xi

yfx() i i

1,0
î=

i

f x

( )

i i

= ?

1, 0 (2.39)

î

Cy

_i

á =

i i

0 yf 0<<

áC

i

á_i

avec :f(x_i) = x i · w+b

==

(2.37) (2.38)

1,0

î i

2.4.1. Optimisation minimale et séquentielle SMO

L'optimisation minimale et séquentielle est un algorithme rapide proposé par platt[21] pour résoudre le problème de programmation quadratique des SVMs sans la nécessiter de stoker une grande matrice en mémoire (matrice de gram) et sans une routine numérique itérative pour chaque sous-problème. SMO décompose le problème de PQ en plusieurs sous-problèmes aussi mais contrairement aux autres méthodes, à chaque étape SMO optimise le plus petit problème possible. Ainsi à chaque étape il optimise deux multiplieurs de Lagrangien. A chaque étape d'optimisation, SMO cherche les valeurs optimales des deux multiplieurs et effectue une mise à jour de la SVM pour donner le reflet des nouvelles valeurs optimisées.

2.4.1.1. Fonctionnement de l'algorithme SMO

L'algorithme SMO comporte trois éléments :

1. Une méthode analytique pour résoudre le problème de PQ.

2. Des heuristiques pour choisir les deux multiplieurs à optimiser. 3. Une méthode pour calculer le seuil b.

2.4.1.1.1. Optimisation analytique des deux multiplieurs du Lagrangien

Les deux multiplieurs de Lagrange doivent satisfaire toutes les contraintes du problème de (PQ) Rappelons que le problème de programmation quadratique pour entraîner une SVM est décrit par les équations (2.34), (2.35) et (2.36). Les contraintes d'inégalité font situer les multiplieurs de Lagrangien à l'intérieur du carré. La contrainte d'égalité les situe sur une ligne diagonale. Par conséquent, une étape de SMO consiste à trouver le (á)

max _á L_D sur le segment de droite délimité

par le carré, avec :

á i^yi

l

á1y1+á2y2=ã ^où ?

ã=-

i3=

ã=á1 ^old +sá 2 old (2.40)

qui dépend á1,á2 ets = y₁.y₂.

ã est une constante, puisque les autre multiplieurs de Lagrangien qui ne vont pas être optimisés sont considérées comme des constantes.

La contrainte sur chaque á_i est : 0 = á_i = C ainsi, les deux multiplieurs se trouvent dans une surface limitée comme le montre la figure 2.5.

On a deux cas d'optimisation selon que y1 et y2 ont le même signe ou pas.

			á1			á1
^0

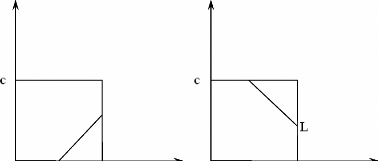
(a) (b)

H

á2

H

á2

Figure 2.5. Deux cas d'optimisation

(a) y₁ ? y₂ (b) y₁ = y₂

· Premier cas (a) :

Implique que : aa ^old _y

₁-= (2.41)

old

2

Les limites de á₂ sont donc :

L ( ?ld )

=max0, a 2 - a (2.42)

?ld

1

H = minC, C +á ₂ - á₁ (2.43)

₍ol'ol'₎

· Deuxième cas (b) :

Implique que : ol' + ol' =

á 1 á 2 ã (2.44)

Les limites de á₂ sont donc :

L = max(0,á 1 ol' + á 2 ol' - C) (2.45)

H = minC,á ₁ + á 2 (2.46)

( ol' ol'₎

l ll

LD (á) peut être exprimée par : LD i yyk =- ^?=^á=^??=^áá ^1 i j ij i j 1 2 1 1 iij

(2.47)

Avec: () ()^T

k ij^Kxi^x j et l

=,á = á₁,K,á

En mettant L_D sous forme d'une fonction de á₂ telle que s = y₁ y₂ , á ₁ =ã - sá ₂ et

l

en posant : ? íi=

^yjj^kij á

on obtient : (2.48)

j 3

1 1 1

=- + - + - -

ãááããáá²

skksk

2

2 2 11112 11 2

2 2 2

L_D ()^á2

^k22^á

2 2

(2.49)

- +

^sk122

ãá

kyyáíãí ²-+ 12 2 111

1

s y á í á 2 2 2 2 -

+

L Cons te tan

l

ll

où : Lyyk

conste i

=-

?á¹ (2.50)

tan 2 ??₌^áá

i j ijij

i=3 3 3

i=j

La dérivée première de L_D par rapport à á2 est telle que :

-

+ sy

y₂í

2 12

- skã

^k12^á

11

í

2

+

2

2

ss++ 1 ã

- + + s sk

1 11

(2)222 122 12(2)2(1 ₂)
ãáááãáíí --+ --+ -
skksksy

(2.51)

?L_D

?á₂

=

- - kk

112 22

áá

k 11

La dérivée seconde de L_D par rapport à á2 est donnée par :

? 2

L_D (2.52)
= - - = ç

2

? _á2 12 11 22

2 k kk

Nous pouvons à pré sent calculer le maximum L_D en permutant uniquement le changement de deux multiplieurs. On définit E_i comme étant l'erreur sur l'ieme exemple d'apprentissage, soit :

E _i =u_i -y_i (2.53)
Où u _i est la sortie fournie par le SVM à l'exemple (x_i, y i ).

l

u yk b 1 á 1 =?=1 j j j - j

(2.54)

On trouve :

í=u+b-yák-syák

1 1 2212 2111 (2.55)

Similairement,

í=u+b-yák-yák

2 2 1112 2222 (2.56)

Au point maximal de LD, l'équation (2.57)

?LD est nulle. Ainsi ?á2

á ã í í

2 11 22 12 11 12 2 1 2 1

( k k k ) s ( k k ) y ( ) s

+ - = - + - + - (2.57)
En substituant (2.55) et (2.56) dans (2.57), nous obtenons :

new old yE-E

()

áá

=- (2.58)

21 2

2 2 ç

Une fois new

á est trouvée, il correspond au maximum sans contraintes. Comme il doit être limité

2

par les points limites de la diagonale on utilise :

?H siH

á new =

2

?

,

á new clipped newnew

= ? áá

si L H

<< (2.59)

2 2 2

? =

?L si L

á new

2

Pour calculer new

á, nous utilisons l'équation suivante :

1

áááá^new newclipped old old

+ = +
ss ^,qui conduit à : 1 21 2

á 1 á 1á ₂ á 2

new =^old+ s ? old - new,clipped?

?? _??(2.60)

Remarque : Quand on évalue ç, la dérivée seconde de L_D avec l'équation (2.52), on constate qu'elle est nulle quand plus qu'un exemple dans les exemples de la base d'apprentissage ont le même vecteur d'entrée x. Dans ce cas, on doit chercher dans ce cas, un autre exemple pour l'optimisation. Sous certaines circonstances inusuelles, ç n'est pas négatif. Alors, SMO évalue (maxL_D) aux deux points de fin du segment. (Voir figure 2.5).

2.4.1.1.2. Choix des deux multiplieurs du Lagrangien

L'algorithme SMO est basé sur l'évaluation des conditions de KKT. Quand tous les multiplieurs vérifient ces conditions, l'algorithme s'arrête. En pratique ces conditions sont vérifiées à une erreur près å.

· Choix du premier multiplieur

D'abord, la boucle externe de l'algorithme effectue une itération sur toute la base d'entraînement pour vérifier s'il existe des exemples qui violent les conditions de KKT. Une fois qu'un violateur est trouvé il est immédiatement choisi pour être optimisé.

· Choix du second multiplieur :

SMO utilise une autre heuristique pour le choix du second multiplieur .Cette heuristique tente de maximiser E₁ - E₂ dans l'équation (2.58). On choisit le multiplieur qui permet de donner la plus grande valeur de cette différence. Rappelons qu'une valeur d'erreur E est déjà calculée pour chaque

exemple dont le multiplieur est différent des limites 0 et C, car c'est à partir de ces exemples que le multiplieur est choisi. Si E1 est positive, l'exemple qui possède la plus petite valeur de E2 est choisi. Si E1 est négative, alors l'exemple avec la plus grande erreur E2 est choisi. SMO utilise, en effet, une hiérarchie dans le choix du second multiplieur. S'il n'y a pas un progrès positif, l'algorithme effectue une itération sur les exemples dont les multiplieurs sont différents de 0 et de C en partant d'une position aléatoire. Si aucun d'entre eux ne permet d'avoir un progrès positif, il reprend la recherche sur toute la base d'entraînement en partant d'une position aléatoire.

Et alors les deux multiplieurs sont conjointement optimisés. A la fin de l'optimisation, le SVM est mis à jour et l'algorithme reprend la recherche des exemples violateurs. Après un passage sur toute

la base d'apprentissage, la boucle externe commence à travailler uniquement avec les exemples dont les multiplieurs appartiennent à l'intervalle ]0, C[ jusqu'à ce que tous les exemples vérifient les conditions KKT. A ce moment, la boucle externe reprend l'itération sur toute la base

d'apprentissage. Elle passe alternativement entre toute la base d'apprentissage et l'ensemble des exemples dont les multiplieurs sont différents de 0 et de C, jusqu'à ce que tous les exemples vérifient les conditions KKT à une erreur å près.

Après avoir trouvé les deux multiplieurs à optimiser conjointement, on calcule leurs valeurs grâce aux formules (2.59) et (2.60) et on met à jour la SVM.

L'algorithme SMO s'arrêt lorsque il ne reste aucun multiplieur de Lagrangien qui viole les condition KKT.

2.4.1.1.3. Mise à jour du seuil b

La valeur de b est calculée à la fin de chaque optimisation.

l

Soit u1 la réponse de SVM avec les anciennes valeurs de á₁ etá₂.

old (2.61)

uykykykb

1 1 1 ¹¹ 2 2 22

=++-

ááá

old old old ^old?111

1

1

=3

Si la nouvelle valeur de á1 est différente de C, alors la sortie du SVM après l'optimisation sera y1.

l

(2.62)

Donc : yykykyk b

= + +-
ááá

new newclipped

,

1 1 111 2212 ?111

1 1

1

3

Nous déduisons ainsi :

b E byky k

=+ + ? -

old new old newclipped old

? ,, ?

1 1 1 1 1 1122

?? áááá

??+? -

?? 2 12

_??(2.63)

De la même manière nous obtenons le seuil b2.

b E by k yk

=+ + ?-

oldnew old newclipped old

? , ?

2 ²¹11 12 22

?? áááá

??+ ? -

?? 2 22

??(2.64)

X2

0

ë

á i = C , î _i >1

è

ô

ä

X1

0<á _i <C , î _i =0

á i = C,0 <î _i <1

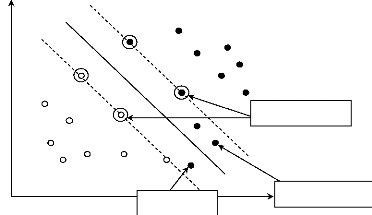
Figure 2.6. Quand les deux multiplieurs sont égaux à la bande C : les vecteurs de support ë et ô donnent le même seuil b. Les points ä et è fournissent les seuils b1 et b2 respectivement. Les points d'erreur et le seuil b se trouve entre b1 et b2.

Si á i = C , dans ce cas, on peut prendre b new +

= comme étant la valeur du seuil.

b ₁ b 2

2

2.4.1.1.4. Mise à jour de l'erreur

Après l'optimisation, lorsqu'un multiplieur de Lagrange possède une valeur différente de C, l'erreur correspondante est mise à zéro. Les erreurs des autres multiplieurs dont la valeur est différente de C et qui n'ont pas été concernés par l'optimisation sont mises à jour comme suit :

E_k= E+u-u (2.65)

new oldnew old

k k k

Nous obtenons ainsi :

EEykykb b

new = + ? -

old new old? newclipped old

, ?old new

kk ?? á á áá

??+ ? -

k ?? ??+ -

k (2.66)

11 1 122 2 2

Dans ce qui suit, nous donnons le pseudo code de l'algorithme SMO.

2.4.1.2. Pseudo-Code de l'algorithme SMO

Target : il contient la sortie désirée (+1 ou -1).

Routine principal

Début

Initialiser les paramètres d 'apprentissage (C, tolérance, epsilon, type de noyau, paramètres du noyau)

Initialiser les multiplieurs á [i] à zéro.

Initialiser le seuil b à zéro.

Chargement de la base d'apprentissage

Numchanged = 0 /* variable qui incrémente pour chaque optimisation des multiplieurs*/ Examineall = 1

Tantque (Numchanged > 0 ou Examineall==1), Faire

Numchanged = 0

Si Examineall= 1, alors

Pour (i= 1 : l), Faire /*répéter i sur tous les exemples d'apprentissage*/
Numchanged= Numchanged+Examine_Exemple (i) /* Exam ine_Exemple est une fonction

est définie plus loin*/

Fin si

Sinon Faire

Pour (i=1, : l), Faire

Si (á[i] != 0 et á[i] != C), alors faire

Numchanged = Numchanged +Eamine_Exemple(i)

Fin si Fin sinon

Si (Examineall == 1), alors faire

Examineall= 0

Fin si

Sinon Faire

Si (Nnumchanged = 0), alors faire

examineall= 1;

Fin si

Fin sinon Fin Tant que FIN

Fonction Examine Exemple(i1)

/*cette fonction permet le choix de deux multiplieurs à optimiser*/

Chapitre2 Machines à vecteurs de support (SVMs)

Debut

y1 = Target[i1]

á1=á[i1]

Si((á1 >0) et ( á1< C)) alors faire

E1= error _cache[i1] /*Error cache calculé par la fonction takestep*/

Fin si

Sinon Faire

E1= (learnedjunction(i1)- y1 /* learnedjunction clacule la fonction de décision*/

Fin sinon r1=y1 *E1

Si rtolérance etCou rtoléranceet )alors faire

(() ()

<-<> >

) ( 0

á á

1 1 1 1

i2= -1

tmax=0

pour i=1, l faire

Si ((á[] > 0) (á[] < ))

ietiCalors faire))

E2= error _cache[i] temp= abs (E1-E2)

Si (temp >tmax) alors faire

tmax= temp

i2= i

Fin si

Fin si

Si (i2= 0) alors faire

Si (takstep(i1,i2) alors retourner 1 Fin si

Fin si

Fin pour

en commençant à une position aléatoire q

pour i=q ,l+q faire
i2=l modulo n

Si ((á[i2] > 0 ) et (á[i2])< C)) alors faire

Si ((takestep(i1,i2) alors retourner1 Fin si

Chapitre2 Machines à vecteurs de support (SVMs)

Fin si Fin pour

en commençant à une position aléatoire q

pour i=q,q+l faire

i2=l modulo q

Si (takestep(i1, i2)) alors retourner1 Fin si

Fin si Fin pour retourner 0

FIN

Fonction takestep(i1,i2)

/* Cette function permet de :- l 'optimisation de deux multiplieurs choisir

-mise à jour du seuil b

- mise à jour de l'erreur */

Début

Si i1=i2 alors retourner 0 Fin si

á1=á[i1]

y1 =target[i1] á2=á[i2]

y2 = target[i2]

S=y1.y2

Calcule L,H

Si (L=H) retourner 0 Fin si

k11 = kernel(exemple[i1], exemple[i1])

k12 = kernel (exemple[i1], exemple[i2]) k22 = kernel (exemple[i2], exemple[i2])

ç 2.k12 - k₁₁ - ^k22

Si (ç<0) alors faire

ááç

22y2.(E1E2)/ ^new=-- Si(^new

á2<L)

á2=L

new

Sinon si ( new

á2>H)

á2=H

new

Fin si

Sinon alors faire

Calculer Lobj et Hobj à partir de (max L_D) en remplacent new

á=L et new

á=H

Si (Lobj>Hobj+ eps) faire

á2=L

new

Sinon si (Lobj<Hobj-eps) faire á2=H

new

Si non faire á2= á2

new

Fin sinon faire

Si (á^new- á<epsá^new+ á+ eps

22 .(22 )) retourner 0 Fin si

á1 new = á1-(2 new 2

s á-á)

Mise à jour du seuil pour refléter le changement dans les multiplieurs de Lagrangien.

Mise à jour de l'erreur pour les autres exemples et mettre les erreurs des multiplieurs qui viennent d'être optimisés à 0.

FIN

5. Conclusion

Ce chapitre a été consacré à la présentation de la formulation mathématique des SVMs et l'algorithme utilisé pour son optimisation. Celle-ci est fondée sur l'utilisation de l'algorithme SMO qui permet l'accélération de l'apprentissage sans la nécessiter de stoker la matrice de Gram en mémoire. Son principe repose sur l'optimisation de deux multiplieurs de lagrangien à chaque étape. Le prochain chapitre sera consacré à l'évaluation des SVMs pour la reconnaissance des chiffres manuscrits.