b. Un découpage harmonieux
Le démiurge partage le mélange en le retranchant
(diaireîn, äécßðåéí),
suivant certaines proportions. Il est nécessaire d'exposer les
règles de base qui constituent ces proportions, même s'il n'est
pas nécessaire d'entrer dans les détails, détails dont la
complexité risquerait de nous égarer. Il convient d'expliquer les
proportions, car si elles ne sont pas le mouvement en tant que tel, elles lui
fournissent les règles sans lesquelles il serait inenvisageable. Le
nombre (arithmos, Üðßèìüñ)
est une pure abstraction obtenue par la raison, agent de mesure et de
beauté. Il n'y a pas de mouvement circulaire qui puisse être
désordonné, car le cercle est associé à
l'idée de perfection et le désordre est synonyme de chaos. Le
mouvement qui anime le monde est donc impérativement lié à
une mesure, sans laquelle il dégénérerait, se
détruirait et ne pourrait pas être. C'est aussi grâce
à la mesure que le démiurge peut découper la
matière en deux bandes24. La bande de l'Autre est
divisée en sept, ce qui correspond au mouvement jugé
irrégulier des sept planètes connues à l'époque de
Platon, c'est-à-dire la Terre [1], la Lune [2], Mercure [3],
Vénus [4], Mars [9], Jupiter [8] et Saturne [27 ou 33]. La
bande du Même représente alors le mouvement apparemment
régulier des étoiles fixes. Il faut rendre compte du mouvement
régulier des corps célestes grâce à la proportion :
« de tous les liens, le plus beau, c'est celui qui impose à
lui-même et aux éléments qu'il relie l'unité la plus
complète, ce que, par nature, la proportion réalise de la
façon la plus parfaite25 ». La bande de l'Autre se
divise en sept, en fonction d'une suite d'entiers positifs : 1 ?1 ; 2?2 ; 3?3 ;
4?4 ; 5?9 ; 6?8 ; 7?27
Ce qu'il est aussi possible de noter en montrant une double
médiété26 géométrique :
23 Voir Chapitre I. 3, a, p. 23.
24 Malgré le fait que Platon nomme les deux
bandes bande du Même et bande de l'Autre, ces bandes
sont bien constituées du mélange du Même et de l'Autre,
cela sans doute pour rendre compte de la différence observée
entre les astres fixes et les planètes.
25 Ibid., p. 120 (Timée 31
c).
26 Platon définit lui-même ce qu'est
la médiété, ou proportion : « Chaque fois que trois
nombres quelconques, que ces nombres soient entiers ou en puissance, celui du
milieu est tel que ce que le premier est par rapport à lui,
lui-même l'est par rapport au dernier, et inversement que ce que le
dernier est par rapport à celui du milieu, celui du milieu l'est par
rapport au premier, celui du milieu pouvant devenir premier et dernier, le
dernier et le premier
|
Première progression
|
20
|
21
|
22
|
23
|
|
Seconde progression
|
30
|
31
|
32
|
33
|
Deux autres types de suites proportionnelles sont
ajoutés : « Après quoi, il combla les intervalles doubles et
triples, en détachant encore des morceaux du mélange initial et
en les intercalant entre les premières, de façon qu'il y ait dans
chaque intervalle deux médités, la première surpassant
l'un des extrêmes tout en étant surpassée par l'autre d'une
même fraction de chacun d'eux, et la seconde surpassant l'un des
extrêmes d'un nombre égal à celui dont elle est
elle-même surpassée. De ces relations, naquirent dans les
intervalles ci-dessus mentionnés, des intervalles nouveaux de un plus un
demi, un plus un tiers et un plus un huitième. À l'aide de
l'intervalle de un plus un huitième, le dieu a comblé tous les
intervalles de un plus un tiers, laissant subsister de chacun d'eux une
fraction, telle que l'intervalle restant fût défini par le rapport
du nombre deux cent cinquante-six au nombre deux cent quarante-trois
27».
Voici un schéma annoté du découpage :

1
2
3
4
8
9
Même Mélange
du Même
Autre et de l'Autre.
27

2/1 2/1 2/1 2/1 3/2 9/8 Gamme
|
Octaves Quinte Ton
|
|
harmonique.
|
|
|
|
La médiété harmonique ajoutée est
traduite ainsi : x-a=a/n et b-x=b/n donc x-a/a = b-x/b = 1/n et (x-a) b= (b-x)a
ou x=2ab/(a+b)
La médiété arithmétique
ajoutée est traduite ainsi : (x-a) = (b-x) ou x= (a+b)/2
En insérant les moyens proportionnels harmoniques et
arithmétiques dans la première médiété
géométrique, cela donne pour les extrêmes :
pouvant à leur tour devenir moyens ». Ibid.,
p. 120 (Timée 32 a). Platon connaissait la
médiété arithmétique, la
médiété harmonique et la médiété
géométrique.
27 Ibid., p. 125 (Timée 36
b).
Pour les médiétés harmoniques : 4/3 ; 8/3 ;
16/3 Et pour les médiétés arithmétiques : 3/2 ; 3 ;
6 Ce qui donne : 1, 4/3, 3/2, 2, 8/3, 3, 4, 16/3, 6, 8.
En insérant les moyens proportionnels harmoniques et
arithmétiques dans la seconde médiété
géométrique, cela donne pour les extrêmes :
Pour les médiétés harmoniques : 3/2 ; 9/2 ;
27/2 Et pour les médiétés arithmétiques : 2 ; 6 ;
18
Ce qui donne : 1, 3/2, 2, 3, 9/2, 6, 9, 27/2, 18, 27.
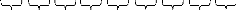
1 4/3 3/2 2 8/3 3 4 16/3 6 8
4/3 9/8 4/3 4/3 9/8 4/3 4/3 9/8 4/3
Les trois intervalles qui subsistent sont 4/3 et 9/8 pour la
première médiété géométrique
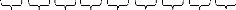
1 3/2 2 3 9/2 6 9 27/2 18 27
3/2 4/3 3/2 3/2 4/3 3/2 3/2 4/3 3/2
et 4/3 et 3/2 pour la seconde.
Ceci correspond en musique pour la proportion 4/3 à la
quarte, pour la proportion 3/2 à la
quinte et pour la proportion 9/8
au ton. En ajoutant l'octave 2/1 -entre la quarte et la quinte- et
le leimma 256/243 -intervalle entre deux tons 9/8-, nous
obtenons un arrangement musical28. L'âme du monde est donc
d'un point de vu musical composée de quatre octaves, une quinte et un
ton : 2/1 x 2/1 x 2/1 x 2/1 x 3/2 x 9/8 = 27
Platon met ici à profit une découverte des
pythagoriciens qui avaient constaté que le son d'un instrument de
musique reste consonant quelque soi la dimension de l'instrument, tant que les
rapports mathématiques entre les cordes restent
égaux29. L'essentiel est le rapport mathématique et
non le son lui-même, car Platon, contrairement aux pythagoriciens, ne
considère pas qu'il existe une musique des sphères
audible30. Platon suppose que l'harmonie (harmonia,
Üðìïíßa) musicale est de la même nature
que celle qui régit les mouvements astronomiques. C'est pourquoi la
musique doit s'efforcer d'imiter l'harmonie divine31. La
parenté entre les deux disciplines est d'ailleurs affirmée dans
La République : « comme les yeux sont attachés
à l'astronomie, de même les oreilles sont attachées au
mouvement harmonique, [...] ces connaissances sont liées l'une à
l'autre comme des soeurs, ainsi que les pythagoriciens l'affirment, et nous
également, [...] qui sommes d'accord avec eux32 ».
Un autre point à souligner tient à l'usage du
mythe fait par Platon. La genèse du monde est un mythe qui a la
particularité d'être conté par un pythagoricien, le
personnage nommé Timée. En effet, le mythe (mythos,
ìýèïñ) n'est pas opposé à la
rationalité (logos, ëüãïñ), et la
philosophie n'est pas opposée à la musique. Le mythe reste un
récit fictif composé par des personnages ; il est fait de
paraboles et d'allégories. Il ne vise pas la vérité, mais
le vraisemblable, répondant aux questions métaphysiques en
interrompant puis en remplaçant l'argumentation et la déduction
par la narration et la suggestion. Le rôle essentiel du mythe est de
porter un sens caché, il est un adjuvant à la réflexion,
ainsi qu'un stimulant moral. De plus, Platon utilise le mythe afin de formuler
des explications de phénomènes que la raison ne peut pas
résoudre, car le logos n'est par principe compatible qu'avec
l'immobile33. Le devenir
28 Pour une étude plus approfondie sur le
thème de la gamme harmonique chez Platon : MOUTSOPOULOS
Evangkélos, La musique dans l'oeuvre de Platon, PUF, Paris,
1959. MOREAU Joseph, La construction de l'idéalisme
Platonicien, Les Belles Lettres, 1936, § 283, pp. 481-484.
29 Voir illustration 1, Annexe p. 64.
30 Op. cit., p. 127 (Timée 37
b) : « emporté sans son articulé ni bruit dans ce qui
se meut par soi-même ».
31 Ibid., p. 200 (Timée 80
b).
32 Op. cit., p. 383 (La
République, VII, 530 b).
33 Ce principe est par ailleurs commun à
Platon et à Parménide, ce dernier disant dans un de ses
poèmes : « Or
c'est le même, penser et ce à dessein
de quoi il y a pensée. Car jamais sans l'être où il est
devenu parole, tu ne
trouveras le penser ; car rien d'autre n'était,
n'est ni ne sera à côté et en dehors de l'être,
puisque le Destin l'a
étant quant à lui par définition
constamment en changement -- principe que Platon tire sans doute de la lecture
d'Héraclite34 --, il n'est en conséquence pas possible
d'en tirer une science. La seule pensée qui puisse expliquer ce que la
raison ne peut pas saisir est donc de nature mythique. Autrement dit, le
discours sur le devenir relève du récit mythique, du
vraisemblable, tandis que la compréhension de l'intelligible
relève de la science, de l'argumentation et des mathématiques.
Les deux axes de la pensée sont unis afin de pallier aux limites de
chacun d'eux, ce qui permet d'exposer le comment et le pourquoi de la formation
de l'univers, ainsi que l'origine du mouvement qui l'anime.
enchai né de façon qu'il soit d'un seul tenant et
immobile ». BEAU FRET Jean, Parménide Le poème,
Paris, PUF, Collection Epiméthée, 1955, p. 87 (le
poème de Parménide VIII-35).
34 «Héraclite dit, n'est-ce pas ? Que tout
passe et que rien ne demeure, et comparant les choses à un courant
d'eau, qu'on ne saurait entrer deux fois dans le même fleuve ».
Op. cit., p. 419 (Cratyle 402 a).
| 


