Résolution de l'équation de kolmogorov par la méthode de fourier

Remerciements

A Monsieur Khaldi Khaled

Maitre de conférences en probabilités-statistique a` l'universitéde Boumerdes et Chef de département de mathématiques

Directeur de these

Monsieur, je vous exprime mes plus sinceres remerciements pour avoir encadrer mon travail pendant cette période de these. Je tiens également a` vous exprimer ma reconnaissance pour votre disponibilité, votre rigueur scientifique, et vos précieux conseils qui ont fait progresser ce travail.

A Monsieur Osmanov Hamid

Professeur d'analyses mathématique a` l'universitéde Boumerdes Directeur de these

Monsieur, je suis tres sensible a` l'honneur que me faites en acceptant de diriger mon travail pendant cette année de these. Je tiens également a` vous exprimer ma reconnaissance pour votre disponibilitéa` tout moment, votre soutien sans faille, soyez assuréde ma sincere estime.

Aux membres de jury

Je suis touchéde l'honneur que vous me faites en acceptant de juger ce travail et d'en être rapporteur. Veuillez accepter mes plus vifs remerciements pour votre présence dans ce jury et soyez assuréde ma profonde gratitude.

A Madame Meddahi-Monsieur Haneche Enseignants au département de mathématiques

Je vous adresse ma sincere reconnaissance pour vos aides et conseils au niveau de la simulation et de la programmation.

A tous mes enseignants de mathématiques, qui m'ont portéde l'aide et de nombreux conseils m'ont étéd'un enseignement précieux.

A mes collègues

Je ne terminerai pas mes remerciements sans avoir une pensésympathique pour mes chers amis Samir, Amer et sans oublier tous mes collègues qui m'ont encouragétout au long de cette année.

Je tiens a` exprimer la fiertede mon père»»Hadj Arab»»ainsi qu'àma mère »»Oum-El-khheir»», source d'amour et de tendresse, pour leur soutient sans relâche durant tout mon parcours pedagogique.

A mon très cher frère Achour.

A mes soeurs Nawel et sarah, que j'aime fort bien.

A ma grande soeur Majdouline, son mari Mohamed, qui m'ont portede l'aide et de soutien.

A l'ange »» Ayate-Errahmane»» qui a volel'amour de nos coeurs.

Je compterai toujours, pour ma part, au nombre des heurs les plus douces, les heureuses de ma vie, celles o`u j'ai pu saisir dans l'espace et étudier sans trêve quelques-uns de ces êtres géométriques qui flottent en quelque sorte autour de nous.

Gaston Darboux

Tables des matières

1. Résumé 8

2. Partie I 'Equation de Fokker-Planck 10

3. Partie II Rappels sur les processus aléatoires 11

(a) Processus aléatoires 11

(b) Mouvement brownien 11

(c) Processus de Bessel 12

4. Partie III Position du problème 15

(a) Problématique 15

(b) Justification de l'équation de Kolmogorov 16

5. Partie IV Méthode de résolution 18

(a) Problème de Sturm-Liouville 19

6. Partie V Présentation des résultats 21

(a) X(t) est un mouvement brownien 21

i. Résolution de la première équation 21

ii. Résolution de la deuxième équation 24

iii. Solution generale 25

(b) X(t) est un processus de Bessel 27

i. Resolution de la première equation 28

ii. Harmonisation de la solution de la première equation

et des frontières 30 iii. Resolution de la deuxième equation 33 iv. Harmonisation de la solution de la deuxième equation				et de la première frontière
34		v. Solution generale
36
A. Première solution		37
B. Deuxième solution		38
C. Troisième solution		38			D. Quatrième solution
39

7. Partie V I Simulation 40

(a) Simulation de Monte-Carlo(rappel) 40

(b) Simulation du mouvement brownien bidimensionnel 41

(c) Simulation du processus de Bessel bidimensionnel 41

8. Conclusion 43

9. Annexe 44

10. Bibliographie 60

R'esum'e

Examinons un processus de diffusion bidimensionnel

X(t) = (X1(t); X2(t)) pour lequel les composantes X1(t) et X2(t) sont ind'ependantes.

Nous voulons 'etudier le probl`eme physique suivant :

Supposons que ce processus bidimensionnel X(t) se trouve dans une r'egion rectangulaire D d'efinie par

D = {(x1, x2 ) ? R² : c1 = x1 = c2;d1 = x2 = d2 }, et que cette r'egion est situ'ee a` l'int'erieur du premier quadrant.

Supposons d'autre part, que le point de d'epart (x1, x2) se trouve a` l'int'erieur de la r'egion D.

Notre probl`eme consiste a` trouver l'expression analytique de la probabilit'e d'atteinte du processus X(t) a` la fronti`ere c2 de l'axe x1 avant toute autre fronti`ere c'est-`a-dire :

P (x1, x2 )= P [X1(T) = c2|X1(0) = x1, X2(0) = x2 ],

o`u

T(x1, x2) = inf{t > 0, X1(t) ?/ (c1,c2)ou X2(t) ?/ (d1,d2)|X1(0) =
x1, X2(0) = x2},

est appel'e le temps de premier passage a` la fronti`ere en question. Cette probabilit'e d'atteinte est donn'ee pour des processus de diffusion

bidimensionnels, parmi eux nous 'etudierons seulement deux : le mouvement brownien et le processus de Bessel.

Pour trouver ce r'esultat, il s'agit en fait,de r'esoudre l''equation de Kolmogorov r'etrograde :

?²P ?P

E²₁{¹₂^- vi(xi) + m_i(xj), } = 0,

?4 oxi

o`u mi et vi sont la moyenne et la variance du processus X(t). Cette derni`ere 'equation est soumise aux conditions fronti`eres de type Dirichlet, telle que P(x1; x2)est nulle en tout cot'e du rectangle except'e en x1 = c2 o`u elle 'egale a` 1.

La solution d'ecoulant de la m'ethode de Fourier connue par m'ethode de s'eparation des variables, est repr'esent'ee sous forme d'une s'erie de Fourier g'en'eralis'ee.

'Equation de Fokker-Planck

Un processus de diffusion est un processus de Markov a` trajectoires continues verifiant l'equation d'Itào

Xt = X0 +

Rt 0

b(s, Xs)ds +

Rt 0

ó(s, Xs)dWs(1.1)

On suppose que b et ó sont des fonctions mesurables, localement bornees sur Rⁿ.

La matrice _(óót)i,j est symetrique et semi-definie positive

i.e.verifie pour tout x E Rⁿ

_in

E,j 0

Soit f une fonction de classe C^1,2 admettant des derivees partielles premi`eres et secondes bornees, et soit Xt une diffusion verifiant l'equation d'Itào independante du temps [1].

.(1.2)

dXt = b(Xt)dt + ó(Xt)dWt

alors on peut definir l'operateur differentiel

f

2

A f = E i bi(x) ^f + 1 E . (óó^t)

?

xi

2

i

,j

^i,j ?xi?xj

?

Une diffusion est caracterisee par :
1. la limite donnant la derive

limh--0 h

E(Xt+h -- Xt | Xt = x)

= b(t, x).

2. la limite donnant la diffusion

E((Xt+h -- Xt)² | Xt = x)

= ó²(t, x).

limh--0 h

3. la condition de Dynkin

= 0.

P[|Xt+h -- Xt| > €|Xt = x]

Vc > 0 limh--0 h

A chaque équation de Itào

dXt = b(t, Xt)dt + ó(t, Xt)dWt

correspond une équation aux dérivées partielles que vérifie la probabilitéde transition ñ(t, x, y) = ñ . Cette équation est dite équation de Fokker-Planck ou équation de Kolmogorov progressive.

?ñ = ?t

?^2(ó^2(t, y)ñ) 1 ^2 ?y2

?(b(t, y)ñ) ?y (1.3).

Il existe une autre équation vérifiée par la densitéde probabilitéqui est appelée équation de Kolmogorov rétrograde (elle porte sur la variable de départ):

?ñ ?t

2ó^2(t, x)^?2ñ ^1 ?x2 + b(t,x)^?ñ ?x(1.4).

En dimension n on note A l'opérateur suivant

A = >:i: i bi(x) ? + 1 >:i: i,j ói,j(x) ?2 . ?xi 2 ?xi?xj

?ñ
?t

L'équation de Kolmogorov rétrograde s'écrit

= Añ.(1.5)

Rappels sur les processus

aléatoires

1. En règle générale, il s'agit d'un processus aléatoire lorsqu'une certaine grandeur aléatoire X(t) varie dans le temps t. On appellera donc processus aléatoire X = X(t) une fonction du paramètre t ? T dont les valeurs X(t) pour chaque t sont des variables aléatoires. En outre, si le passage d'un état ultérieur n'a de dépendance qu'envers l'état présent,le processus est dit markovien, et particulièrement de diffusion si ces changements continuels d'état se font au sein d'un espace continu d'état.

2. Mouvement brownien

Soit Wt = (W t 1, W t 2) un processus de diffusion bidimensionnel,telles que ces composantes sont indépendantes.

Nous dirons que (Wt; t = 0) est un mouvement brownien bidimensionnel si pour tout i = 1, 2 (W t i ; t = 0) est un mouvement brownien unidimensionnel.

D'efinition:

Le processus (Wt; t = 0) est dit mouvement brownien si:

(a) P(W0 = 0) = 1.

(b) ?s = tWt - W_s N(0,t - s).

(c) ?n,?ti;0 = t0 = ... = t_n : (Wt_n - Wt_{n 1}, ..., Wt1 - Wt0) sont indépendantes.

(d) ?t = 0,la fonction t 7? Wt est continue presque surement.

3. Processus de Bessel

Soit une équation différentielle stochastique

Xt = Z + _Rt b(s,X_s)ds + _Rt a(s, X_s)dW_s, (2.1)

0 0

cette équation est équivalente a`

dXt = b(t, Xt)dt + a(t, Xt)dWt, (2.2)

Xt représente l'unique solution de (2.2) et justifiable le fait que b et a vérifies le théorème d'existence et d'unicitédes solutions des E.D.S. Une classe importante des E.D.S. dont l'existence et d'unicitésont montrées en appliquant des théorèmes du calcul stochastique¹, est la suivante [16]:

Xt = x + 2 _Rt vX_sdW_s + 8t.(2.3),

0

o`u (Wt; t = 0) est un mouvement brownien standard réel; x, 8 > 0.

¹Théorème 2.1: [16]

supposons que a et b sont a` croissance linéaire, c'est-à-dire,satisfont la condition de Lipschitz locale, et que

|a(t, x) - a(t, y)|² = p(|x - y|), Vt = 0 avec p :]0, +8[-?]0, +8[ est

une fonction borélienne telle que Vå > 0 :

Rå 0

dz p2(z) = +8.

Alors si Z = x E R l'équation (2.1) admet une solution forte et unique, c'est-à-dire VB E , Vô E Ft(temps

d'arrêt),Vh = 0 : P[Xô+h E B/Ft] = P[Xt+h E B/X_ô] avec est la tribu des boréliens.

Donc (2.3) admet une unique solution forte. X est appeléprocessus de Bessel carréde ä-dimension.

Nous allons relier le processus de Bessel au brownien. Soit n = 2 W = (W¹, W²) un mouvement brownien bidimensionnel.

Soit X le processus définit par Xt = ||Wt|| alors X2 t = P2 i=1(Wti)2, et la formule d'Itômontre que

dX2 t = 2 2 i=1 W t i dW t i+ 2dt.(2.4)

Notons (x, y) le produit scalaire des vecteurs x et y, on voit que le processus â définit par:

? ? ?

1 1 P2 dâ = (Wt, dWt) = i=1 W t i dW t i Xt ||Wt|| â0 = 0

(2.5)

est une martingale continue, de carréintégrale, et la formule ^d'Itômontre que (â2 t - t; t = 0) est une martingale.

La caractérisation de Paul-Levy montre que (ât; t = 0) est un mouvement brownien [16].

dX2 t = 2(Wt,dWt) + 2dt

s'écrit

dX2 t = 2Xtdât + 2dt

En effet,

dX2 t = 2>2 i=1W t i dW t i= 2(Wt,dWt)+2dt.

or

(Wt, dWt) = Xtdi9t

=dX2 t = 2Xtdi9t + 2dt.

Si on pose Vt = X2 t ,on obtient que V est la solution d'une E.D.S.de type (2.3)

c'est-à-dire

dVt = 2vVtdi9t + 2dt,

o`u (i9t, t = 0) est un mouvement brownien.

Appliquant de nouveau la formule d'Itôa` (Xt, t = 0) on obtient

2 - 1dt dt

dXt = di9t + = di9t + .

2 Xt 2Xt

On dit que (Xt; t = 0) est un processus de Bessel de 2-dimensions. Remarques:

(a) Zt = logXt est une integrale stochastique par rapport a` i9t.

(b) Soit v un nombre reel positif :

_v²_ft ds

Lt = [Xt]^vexp(-) est une martingale locale. 2 X2

0 s

(c) Soit l'E.D.S.

8 - 1

dYt = di9t + dt ,

2Yt

(Yt) est un processus de Bessel de dimension 8.

Part III

Position du problème

1. Problématique

Soit un processus de diffusion de dimension 2 : Xt = (X1(t), X2(t))

dont les composantes X1(t), X2(t) sont indépendantes. Soit aussi T(x1, x2) la variable aléatoire associée a` l'instant de premier passage

du processus Xt a` la frontière d'une région rectangulaire finie D :

D = {(x1,x2 )E R² : c1 = x1 = c2;d1 = x2 = d2 } .

laquelle région est située a` l'intérieur du premier quadrant. Supposons que le point de départ (x1, x2) du processus Xt est nécessairement de cette région.

Nous définissons la probabilitéde premier passage [2] par

P (x1,x2 )= P [X1(T) = c2|X1(0) = x1,X2(0) = x2 ] cette probabilitéest donnée par deux processus stochastiques

bidimensionnels, le mouvement brownien et le processus de Bessel.

Pour arriver a` la concrétisation de P(x1, x2) , il s'agit en fait de résoudre l'équation de Kolmogorov rétrograde, qu'on va démontrer plus tard :

P2 i=1{1 ₂vi(xi)^o2P + mi(xi) ^oP} = 0, (3.1) ox² oxi

i

o`u mi(xi) = E(Xi),vi(xi) = V ar(Xi),avec les conditions aux limites :

P(c1,x2) = 0,x2 E [d1;d2]
P(x1 = c2,x2) = 1,x2 E [d1;d2].

La solution de (3.1) découle de la méthode de séparation des variables ou méthode de Fourier.

On definit l'instant de premier passage par ([2], [5])

T(x1, x2) = infft > 0, X1(t) ?/ (c1, c2) ou X2(t) ?/ (d1,d2)|X1(0) =
x1, X2(0) = x2}.

Une facon d'aborder ce type de probl`eme est de considerer que la fronti`ere d'atteinte est absorbante avec probabilite1. ([5], [11])

2. Justification de l''equation de Kolmogorov (3.1) : Comme nous avons dit dans la premi`ere partie l'equation de Fokker-Planck est donnee par :

_~1 ~ ~ ~

?ñ = P2 2Sij(x) ?2ñ + ^P2 mi(x) ^?ñ , (3.2)

i,j=1 i=1

?t ?xixj ?xi

avec ñ limit'ee par les quartes fronti`eres est donn'ee par

ñ(t , x 1, x2, u, v) = 1

dudv P[X1(t) ? (u, u + du), X2(t) ? (v, v + dv)]

est la densitedu processus Xt.

Puisque les termes de covariances pour X1(t),X2(t) sont nuls, (3.2) sera equivalente a`

?ñ
?t

_~1 ~ ~ ~

= P2 ₂vi(xi)^?2ñ + ^P2 mi(xi) ^?ñ .(3.3)

i=1 ?x2 i=1 ?xi

i

Puisque (3.3) est homog`ene dans le temps.

Supposons que Ö(t) est la fonction de repartition de la variable aleatoire T(x1, x2), donc

d2 c2I - Ö(t) = P [T (x1, x2) = t = f f ñ (x1, x2, u, v,t)dudv ,

d1c1

et Ö^'(t) = ö(t) notee ö(t/x1, x2) est la fonction densitede T(x1, x2).

Soit la transformée de Laplace q^*(t/x1, x2) de la fonction q(t/x1, x2) :
ö* (s|x1, x2 )= Ee-sT(x1,x2)

= _R8 e^-stq (t|x1, x2 )dt.

0

D'après le résultat classique de probabilitéfondamentale cette transformée de Laplace satisfait

P2

+ mi(xi)^?ö*
i=1{1 ₂vi(xi)^?2ö* } = sq^*, (3.4)
?x² ?xi
i

avec les conditions évidentes :

ö* (s|c1, x2 )= ö^* (s|c2, x2 )= ö^* (s|x1, d1 )= ö^* (s|x1, d2 )= 1,

ö(t|x1, x2) comporte 4 branches correspondant a` autant de frontières et peut être écrite

q (t|x1, x2 )= _öc1 (t|x1, x2 _)+öc2 (t|x1, x2 _)+öd1 (t|x1, x2 _)+öd2 (t|x1, x2 ).

Alors qi (t|x1, x2 ) est la fonction de densitéde l'instant de premier passage a` la frontière i dont la probabilitéd'absorption se donne a` la frontière i.

Si le problème est modifiéde facon a` ce que l'instant ne soit maintenu

que pour la frontière j, la fonction q^* sera posée nulle pour toute autre frontière exceptépour celle en cause, et la résolution de l'équation (3.4) conduira vers l'expression de q* j (s|x1, x2 ) .

La limite de cette dernière lorsque s tend vers 0 est la probabilitéque X(t) soit absorbéa` la frontière j. On obtient :

P2 i=1{1 ₂vi(xi)^?2P + mi(xi) ?P } = 0. ?x² ?xi

i

Part IV

M'ethode de r'esolution

Pour le problème d'endroit de premier passage, il n'est methode de resolution mieux adaptee a` ce type de problèmes bidimensionnels que celle de Fourier.

Soit l'equation de Kolmogorov retrograde :

^2P ?P

E_{i 1{21vi} (xi) ₂ + mi (xi) ,₁ = 0. (4.1)

?x_i Oxi

La methode de Fourier consiste a` poser :

P(x1,x2) = ?(x1)ø(x2).(4.2) Donc on aura l'equation :

A2 (n(x_i)ø (x2) ??(x1)ø (x2)} = 0.

Ei2 { 21 vi (xi) - #177; Til_z (X_i)

?4 ?xi

En devisant les deux membres de cette equation par ?(x1)ø(x2) on obtient

(x1)^?(x1)

2 ?(x1) ?x1)

2 v2(x2)

1 ø(x2)

ø(x2) m1 (x2)

ø(x2) = ë.

^II(x1)

1

?

v1x1)

Nous obtenons deux equations differentielles

1

2

1

2

v2(x2)ø^"(x2) + m2(x2)ø^'(x2) + ëø(x2) = 0.(4.3)
v1(x1)?^0"(x1) + m1(x1)?^'(x1) - ë?(x1) = 0.(4.4)

ë sont appelees valeurs propres auxquelles sont associees des fonctions propres.

Il s'agit en fait, de resoudre le problème de Sturm-Liouville.([20], [22])

1. Problème de Sturm-Liouville

Soit l'équation de Sturm-Liouville

~ ~

d p(x)^dy - q(x)y + Ar(x)y = 0.(4.5)

dx dx

x ? [a,b],p > 0,r > 0,q = 0.

Toute équation différentielle d'ordre 2 peut être mise sous la forme (4.5). Nous construisons la solution de (4.5) vérifiant les conditions frontières :

? ???

???

(4.6)

c1y^'(a) + c2y(b) = 0
â1y^'(a) + â2y(b) = 0
c2 1 + c2 2 =6 0
â²₁ + â2 2 =6 0

La recherche des nombres A et des fonctions y(x) non identiquement nulles, solutions de (4.5) et vérifiant (4.6) , s'appelle problème de Sturm-Liouville.

Proposition 4.1. [21]

Il existe une suite infinie de valeurs propres (0 peut ne pas être valeur propre)formant une suite croissante:

-8 = A0 = A1 = ... = A_n...

avec _limn?8 A_n = +8.

Proposition 4.2. [22]

Les fonctions propres y1(x), ..., y_n(x) forment un système orthogonal par rapport a` la fonction poids r(x)

Rb a	{ 0 si k =6 m r(x)yk(x)yn(x)dx = u2 n si k = m (4.7)

Proposition 4.3. [21]

Si les conditions aux limites telles que

p(x)y(x)y'(x) |^b _a= 0

alors toutes les valeurs propres sont strictement positives. Proposition 4.4. [22]

N'importe quelle 'equation diff'erentielle d'ordre 2

A(x)y^" + B(x)y⁰ + (ëC(x) - D(x))y(x) = 0, peut se ramener a` la forme (4.5) si A(x) =6 0.

En effet,

On multiplie cette 'equation par ñ(x), et on suppose que

x_cr, B(t)

B - A' ñ(x) = exp (J A(t)

- A^' (t) dt .

)

ñ =

(Añ)^' = B ñ A

ñ

Dans ce cas notre 'equation de d'epart s''ecrit :

(Añy^')^' + (ëCñ - Dñ)y = 0

On pose A(x)ñ(x) = p(x), C(x)ñ(x) = r(x), D(x)ñ(x) = q(x). On obtient donc

(p(x)y⁰(x))^' + (ër(x) - q(x))y = 0.

111

Revenons a` l''equation (4.2) si celle-ci est multipli'ee par

x2 )

ñ(x2) = exp (f 2m2 (x2) dx2

0 v2(x2)

alors on obtient l''equation de Sturm-Liouville :

? ? ~x2R ~

2m2(x2)

~x2R ~ 2ëexp ø

? 2m2(x2) ? v2(x2) dx2

? ?exp ø0 ? 0 + 0

v2(x2) dx2 = 0 ,

? v2(x2)

0

Alors par identification :

(x²₇.₍ 2m2(x2) dx2)

p(x2) = exp

0 v2(x2)

q(x2) = 0,

r(x2) =	2exp (^xf^2m2(x2)dx2) 0 v2(x2)	2p(x2) = v2(x2) .
	v2(x2)

Part V

Presentation des resultats

1. X(t) est un mouvement brownien:

Pour ce processus stochastique on a :

mi(xi) = ui E R vi(xi) = ó2 i strictement positive. La méthode de Fourier conduit aux deux équations:

ø00 + 2u2 ø, + ^2ë ø = 0.(5.1)

_ó2 _ó2

2 2

+ ?

ó2 ₁

2ë

⁰ - ? = 0.(5.2)

ó2 ₁

00

?

2u1

(a) Resolution de la premi`ere equation Soit l'équation différentielle :

ø00 + 2u2 ø, + ^2ë ø = 0.

_ó2 _ó2

2 2

+

2u2

00

ù

⁰ +

ó 2

ù

2

2ë

Posons x2T = x2 - d1 E [0, _d2T] ^avec d2T = d2 - d1 et ø(x2) = ù(x2T). De cela, il vient que:

ù = 0

ó2 ₂

L'équation caractéristique est :

2u2 2ë

K2 + K + = 0.(5.3)

_ó2 _ó2

2 2

admet comme solution

K1,2 = -^u2 #177; ó2 2

1 \/ u2 2 - 2Aó^2 2. ó2 2

Il est facile de voir qu'il y a 3 cas a` analyser 1)u2 2 > 2Aó² ₂, 2)u2 2 = 2Aó² ₂, 3)u2 2 < 2Aó² ₂.

(1).u2 2 > 2Aó2 2

On distingue deux racines réelles K1 et K2 alors

ù(x2T) = C1e^K1x2T + C2e^K2x2T. Vérifions les conditions aux limites

ù(x2T = 0) = C1 + C2 = 0 = C1 = -C2.
ù(x2T = d2T) = C2(e^K1d2T - eK2x2T) = 0

ceci n'est réalisable que si ,d'une part, C2 = 0, ou si , d'autre part, K1 = K2, ce qui contredit le fait que K1 =6 K2. Donc cette solution est bien rejetée.

(2).u2 2 = 2Aó2 2

La solution para^àit comme suit :

u2x2T

-

ù(x2T) = C1e

u2x2T

2

ó 2 .

-

ó2 2 + _C2x2T e

On vérifie les conditions aux limites on obtient :

ù(x2T = 0) = C1 = 0,

u2d2T

ù(x2T = d2T) = C2d2Te

ó22 = 0,

ce qui est possible seulement si d2T = 0 ou C2 = 0, donc cette solution est aussi bien refusée.

(3). u2 2 < 2Aó² ₂.

Il y a deux racines complexes conjuguées:

K1,2 = -^u2 #177; i ó2 2

1 \/2Aó2 2 - u2 2 = a2 #177; ib2. ó2 2

-u2

avec a2 =

ó 2

.

2

De sorte que ù(x2T) = ea2x2T

{C1 cos(b2x2T) + C2 sin(b2x2T)}. Verifions les conditions aux limites:

ù(x2T = 0) = C1 = 0,
ù(x2T = d2T) = C2e^a2d2T sin(b2d2T) = 0.

Si C2 =6 0 donc sin(b2d2T) = 0 ? b2d2T = nð, n ? {1, 2, 3...} Donc la solution est

~ _nð ~

ù(x2T ) = C2e^a2x2T sin x2T .

d2T

Maintenant pour C2 = 1

~ _nð ~

ù(x2T ) = ea2x2T sin x2T .

d2T

Maintenant pour la constante ë on a :

,2 { _n2_ð2 ₁₁2

² + ²

2 AT #177; ó2 }

ë_n = " ,n ? {0, 1, 2, ...}.

2

Remarquons que (ë_n) ? et que lim_n, ë_n = +cc, d'apr`es le theor`eme de Sturm-Liouville, on correspond des fonctions propres ù_n a` chaque ë_n

~ _nð ~

ùn(x2T ) = C2e^a2x2T sin x2T , n = 0.

d2T

(b) R'esolution de la deuxi`eme 'equation

Soit l'equation differentielle :

+

2u1

00

?

2 ? 1

2ë_n

⁰ - ₂? = 0.

ó₁

Comme precedemment, on pose x1T = x1 - c1 ? [0, c2T ] , avec c2T = c2 - c1.

En outre, on pose ?(x1) = ù^*(x1T) on aura l'equation

ù*,, + 2u1 ù*0 - 2ënù* = 0.(5.4),

_ó2 2

ó₁

ainsi, l'equation caracteristique reliee a` cette derni`ere expression

2u1 2n= 0,

K2 + ₂ K

2

ó₁ ó₁

laquelle admet les solutions reelles:

#177; u1 K1,2 = -2 ó1 Donc la solution est

12 Vu^21+ 2ënó = a1 1

ù^*(x1T) = A_ne^K1x1T + BneK2x1T = ea1x1T {A_ne^b1x1T + Bne-b1x1T}

n ? {1,2,3...}.

Verifions la condition fronti`ere x1T = 0

ù^*(x1T = 0) = A_n + B_n = 0 = A_n = -B_n.

Donc

ù^*(x1T) = Bnea1x1T {_e-b1x1T -_eb1x1T} = -2B_ne^a1x1T sh (b1x1T).

(c) Solution g'en'erale

Nous avons poseP(x1, x2) = ?(x1)ø(x2) ce qui revient a` dire que P(x1, x2) = ù^*(x1T)ù(x2T). Donc la solution generale est une serie de Fourier generalisee de la forme :

~ _nð ~

P (x1T , x2T) = E8n=1 --2B_ne^a1x1T sh (b1x1T) ea2x2T sin x2T .(5.5)

d2T

Pour trouver le coefficient de Fourier, on evalue P _(x1T , x2T) a` la fronti`ere

c2T.

P (x1T = c2T, x2T) =

( _nð ~

E8n=1 --2B_ne^a1c2Tsh (b1c2T) _ea2x2T sin x2T = 1.

d2T

Exhibons tous les termes independants de n :

~ _nð ~

_e-a2x2T = E8n=1 --2B_ne^a1c2Tsh _(b1c2T) sin x2T .

d2T

(n ^,ð

Multiplions les deux membres par : sin x2T , et en integrant sur

d2T

(0, d2T), on a :

d2T

0

~n,ð ~

_e-a2x2T sin x2T dx2T =

d2T

d2Tf 0

~ 2 nð sin d n^' --2B^a1c2Th (b ) nesic2T sin 7 x2T sin x2T) x2T d2T d2T

Supposons que la serie a` droite est uniformement convergente donc integrable terme a` terme.

En tenant compte de l'orthogonalitedes fonctions sinus on obtient :

d2Tf 0	(n^0ð e sin x2T)dx2T ^--a2x2T i ,..7 Ct2T
=-2Bn^,e^a1c2Tsh (b1c2T)		d2Tf 0	sin2 (nd x2T) dx2T = uv2T

(b

1c2T

)

²

.

-2Bn,ea1c2Tsh d2T

Le coefficient de Fourier est liea` l'integrale qui prec`ede de la facon suivante :

2 d2T n ð

-2Bn, ea1c2T

(b1c2T) = d f _e-a2x2T sin x2T)dx2T

w2T 0 d2T

En calculant cette integrale, on obtient :

Bn =	-nð {(-1)^n+1e^-a2d2T + 1}
	(a22d22T + n^2ð^2) e^a1c2Tsh(b1c2T)^.

Donc la solution generale dans le syst`eme des references originales

x2T = x2 - d1; x1T = x1 - c1 est :

P (x1, x2) =

En8 C_ne^a1(x1-c1)sh [b1 (x1 - c1)] ea2(x2-d1)sin [ mr d2 - d1 (x2 - d1)] ,

o`u

Cn =	2nð^{(-1)n+1e-a2(d2-d1) + 1} (a^22(d2 - d1)^2 + n^2ð^2) e^a1(^c2-^c1)sh(b1(c2 - c1))^;

a1 = -u1 ó12 ;

b1 = 12 Vu²₁ + 2ë_nó²₁;

1

ó2 ( n²ð² ë_n = .

(d2 - d1)2 + u2 ₂ 2 ó2 ₂

2.X(t) est processus de Bessel:

Le processus de Bessel en est un qui représente la distance euclidienne a` l'origine d'un mouvement brownien multidimensionnel.

Ainsi si l'équation de Kolmogorov rétrograde est établie de façon a` ce que : [5]

ái - 1

mi(xi) = , (ái = 0) et vi(xi) = ó2 i > 0,

2xi

alors elle caractérise un processus du Bessel, et les équations différentielles

ø00 + á2 - 1 ø, + ^2ë ø = 0, (5.6)

ó2 2x2 ó2 ₂

et

00 ?

á1 - 1 + ? ó2 1x1

2ë ^0 - ? = 0, (5.7) ó2 1

sont celles obtenues par la méthode de Fourier.

D'efinition:

Une frontière est dite accessible si la probabilitéqu'elle soit atteinte par le processus en un temps fini est supérieure a` zéro, sinon elle est dite inaccessible.

On admet que la dénomination aux frontières régulières et de sortie est maintenue.

Donc ces dernières sont accessibles dans le sens o`u l'atteinte de celle-ci par le processus en un temps fini est une éventualité.

En opposition, sont qualifiées d'inaccessibles les frontières d'entrée et les frontières naturelles.

Supposons aussi que l'origine est un point pour le processus de Bessel dont l'atteinte ou non par ce processus dépend du lien de grandeur qui unit les paramètres á et ó².

D'autre part, si ái = ó2 i + 1 pour i = 1, 2 alors tout point est accessible incluant l'origine, particulièrement, si 1 - ó2 i = ái = ó2 i + 1, zéro est une frontière d'entrée et manifestement inaccessible. [4]

(a) R'esolution de la premi`ere 'equation:

Soit l'équation

ø00 + á2 - 1 ø, + ^2ë ø = 0.
ó2 2x2 ó2 ₂

Il parait que deux cas sont a` analyser: ë = 0 et ë =6 0.

Si ë = 0

ø00 + á2 - 1 ø, = 0.
ó2 2x2

Posons u = øⁱ u^' = ø⁰⁰. On aura u^' + á2 - 1 u = 0.

ó2 2x2

Donc la solution est

1 - á2

u = ùx 2 ó2 ₂ = ø^'.

= ø(x2) = ù1x^2â2

2 + ù2,

avec â2 =

ó2 2 - á2 + 1

.

2ó2 2

Cette dernière est valable ó2 2 =6 á2 - 1.

Dans le le cas contraire on a :

ø(x2) = ù1log(x2) + ù2.

'Evaluons les solutions aux fronti`eres :

* pour la premi`ere solution :

ø(x2 = d1) = ù1d1 2â2 + ù2 = 0

ceci n'est vrai que si ù2 = -ù1dr². Ainsi

ø(x2 = d2) = ù1(d^2â2

2 - d2â2

1 ) = 0

et puisque

d1 =6 d2,et â2 =6 0 = ù1 = ù2 = 0

Donc cette solution est rejetée. *pour la deuxi`eme solution :

ø(x2 = d1) = ù1log(d1) + ù2 = 0 = ù2 = -ù1log(d1).

ø(x2 = d2) = ù2(log(d1) - log(d2)) = 0

et puisque d1 =6 d2 donc

ù1 = ù2 = 0 .

Donc la solution est rejetée, et par extension ë =6 0.

Soit ë =6 0 la solution générale est : [9]

ø(x2) = 42 fù1Jv(vb2x2) + _{ù2Yv(vb2x2)},} (5.8) 2ë

22 - á2

oii. v = |â2| ? R⁺ , b2 = ó2 , â2 =

.

0

2 2ó2+ 1

2

Les fondements du problème imposent que A > 0. Car dans le cas contraire vb2 serait purement imaginaire, la solution ferait donc appel aux fonctions de Bessel modifiées, lesquelles n'admettent des zéros, d'une part, qu'àx = 0 pour la fonction I_v(x), et d'autre part, qu'àx ? 8 pour la fonction K_v(x), ces fonctions n'ont pas le caractère oscillant exigé.

(b) Harmonisation de la solution de la premiere 'equation et des frontieres:

Soit les formes limites des fonctions de Bessel pour des arguments se rapprochant de zéro et pour ç réel et fixé: [17]

(x ~ç 1 Jç(x) ' F(ç + 1) 2

,ç =6 -1,-2,...(5.9)

_{(2 )ç}

-1 F(ç) si ç =6 -1, -2...

ð x

log(x), si ç = 0

2

ð

(5.10)

? ??

??

Y_ç(x) '

cas oüd1 = 0

Nous avons â2 = v lesquelles valeurs sont strictement positives de sorte que 0 = a2 < O2 2 + 1.

~ W1 (vb2x 2 _~v ( ₂ )v}

- W2

limx2?0 (x2) = limx2?0 xv ð F(v)

² vb2x2

F(v + 1) 2

( ₂ )v

-W2

= F(v) _vb2 .(5.11)

ð

~ ₂ )v

-W2

Donc (x2 = 0) = F(v) _vb2 = 0 = W2 = 0.

ð

On obtient

ø(x2) = ù1x^v ₂J_v(vb2x2).(5.12).

'Evaluons a` la frontiere x2 = d2

Ù

ø(x2 = d2) = ù1d^v2Jv(vb2d2) = 0 ?vb2 = Kvn = , v > 0,n ? {1, 2, ..}

dⁿ2

Remarque:

Utilisant le resultat connu sur J_v(kx) = 0,Ùvn est la ^ni`eme racine de la fonction de Bessel de premiere espece d'ordre v et le nombre de ces racines est infini.

Puisque vb2 = Ùvn

d2 ó² ó2

= =

\/ 2ë v2ë

2 .

Alors ë se trouve en un nombre infini, on les notes ë_n qui peuvent notes

par

ó2 2K2 vn ën = 2

> 0.

D'apres le probleme de Sturm-Liouville,on fait correspondre a` chaque valeur propre ë_n une fonction propre ø_n(x2).

Donc

Ù

ø_n(x2) = x^v₂J ^vnv(Kvnx2) = 4,4( _j x2), n = 1.

a2

cas o`u d1 > 0

Si 0 = á2 = ó²₂ + 1, alors â2 = v(6= 0),d1 peut àetre positif, par contre,si á2 = ó²₂ + 1 ,â2 est negatif et est de signe opposea` v lequel peut àetre nul. d1 n'est alors autrement que positif, donc l'evaluation de la solution aux frontieres conduit a` un systeme dont les constantes ù1 et ù2 de la solution constituent les termes variables.

1

ù1Jv(vb2d1) + ù2Yv(vb2d1) = 0 ù1Jv(vb2d2) + ù2Yv(vb2d2) = 0 (5.13)

Le syst`eme admet une solution non triviale, pour ù1, ù2, si et seulement si le determinant :

Ä = ~~~~

Jv(Vb2d1) Yv(Vb2d1) Jv(Vb2d2) Yv(Vb2d2)

~~~~

soit egale a` zero,

et les racines positives de cette equation transcendante determinent les valeurs propres.

Acceptons que

--Y_v(Vb2d1)

Jv(Vb2d1)

Jv(Vb2d2) .(5.14)

ù1

=

ù2

^--Yv(Vb2d2)

Notons le rapport multipliepar --1 des fonctions Y_v et J_v par R(d1,d2)

2,v .

Donc la solution est

_n

R₁1_,- ⁴²) T_v /1, \ \ \

ø(x2) = ù242 ^d (_v u2x2)+ v(Vu2x2)} .(5.15).

Designons les racines Vb2 du determinant Ä par _KÄvn, il resulte que

_KÄ

vn

,n E {1, 2,...}.

_V

2ë

ó2

Puisque ë_n sont infinis = K^Ävn le sont. Posons

ó2 2(KÄ vn)2 ën = 2 Donc la solution generale est

.(5.16)

nøn (x2) = ù242 ^,d2) J_v (K_v^Ä_nx2) Yv(K_v^Ä_nx2)} .(5.17).

ø_n(x2) =x^â2

2 Fv(KÄvnx2).(5.18).

(c) R'esolution de la deuxi`eme 'equation:

II ?

á1 - 1 + 2 ? ó1x1

0 2ë - ? = 0. ó^21

La solution de cette équation différentielle est donnée par : [9]

?(x1) = 4_.¹ fAnJs(vb1x1) + _BnYs(vb1x1)} , (5.19)

o`u s = |â1| ? R⁺,b1 =

-2ë 2

ó₁ - á1 + ¹

,

1

² 2ó2

1

â1 =

ó

v2ë_n

.

Puisque ë_n > 0, alors vb1 = i

ó1

Donc

ó^T,vó1

?(x1) = xP^- {A_nJ_s(i x1) + B_nY_s(i x1)} .(5.20)

ëë_n

?(x1) = x^li^'_.¹ {A_nJ_s(iNAb1|x1) + B_nY_s(i^,\Ab1|x1)} .(5.21) Remarquons qu'une valeur réelle de x1 peut résulter en une évaluation complexe de la fonction.

Raisonnons autrement comme suit :

Si xP^- Js(i ^V |b1|x1) est solution de l'équation différentielle alors _i-s 41 J_s (i V|b1|x1) l'est aussi.

Or, cette derniere expression est une fonction réelle pour tout x1 réel, et contient la fonction de Bessel modifiée de premiere espece notée I_s : c'est-`a-dire on substitue le terme 4¹J_s(iV |b1|x1) par 4¹I_s(V|b1|x1).

D'une facon analogue, si 4¹Y_s(iV |b1 |x1) est une solution , donc 4¹ K_s(V|b1|x1)
l'est aussi. K_s est la fonction de Bessel modifiée de deuxieme espece.

Sachant que :

ði^s+1

xP-Ks( ^V |b1|x1) = 2 xâ1 {Js(iNAb1|x1) + iY_s(iV|b1|x1)} .(5.22)

1

Finalement, la solution est :

?(x1) = xP^- {A_nI_s(V |b1|x1) + B_nK_s(V |b1|x1)} .(5.23)

(d) Harmonisation de la solution de la deuxi`eme 'equation et de la premi`ere fronti`ere :

Soient les formes limites des fonctions de Bessel modifi'ees : [17]

I_ç(x) ,-, 1 _(x)ç

, si ç =6 -1, -2, ...(5.24)

(ç + 1) 2

Kç(x) ,-'

{

-log(x) ,si ç = 0 2(ç)^(2)ç, si ç > 0 (5.25)x

cas o`u c1 = 0

Ceci est permis que si 0 = á1 = ó²₁ + 1, et alors â1 = s(> 0et =6 0).

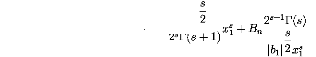
limx1_>.0 ?(x1) = limx1_>.0 xâ1

1

|b1|

2^s(s + 1)x1 n s

A_n

{

s

2

^s + B 2s-1(s)

|b1|2 x^s₁

}

B 2s-1(s) = -"n s		> 0.
	{		ó2Kvn	si d1 = 0 si d1 > 0
avec V|b1 | =			ó1 ó2K^Ävn ó1

|b1| 2

Donc ?(x1 = 0) = Bn 2s-1(s) s = 0 B_n = 0

|b1| 2

?(x1) = A_nx^s₁I_s(V|b1|x1).(5.26)

cas o `u c1 > 0

Si 0 < á1 < ó²₁ + 1, alors â1 et s sont strictement positifs et sont égaux, (c1 peut àetre positif).

Ainsi, dans le cas o`u á1 > ó<sup>2</sup><sub>1</sub> + 1, â1 et s sont égaux en valeur absolue et inférieurs ou égaux a` zéro.(c1 n'est autre que positif)

L'évaluation a` la première frontière conduit au résultat :

co(x1 = c1) = 41 { A_nI_s(V |b1|c1) + B_nK_s(V |b1|c1)} = 0

....	An	--Ks(V| b1 | c1)	= R(c1) 1,s .(5.27).
	_ Bn	IsMb1 | c1)

Ceci justifie l'expression

co(x1) = BnxP- { R⁽₁7_,¹₉⁾ I_s(_NAb1|x1) + Ks(NAb1|x1)} =
B_nxP^-G_s(V|b1|x1).(5.28).

	{	ó2Kvn	si d1 = 0 si d1 > 0
avec V|b1 | =		ó1 ó2K^Ävn ó1

(e)Solution g'en'erale pour le processus de Bessel :

Avant de donner les formes de la solution générale, voici quelques propriétés essentielles:

Proposition 5.1.(Orthogonalitédes fonctions de Bessel)[17][24]

l f 0

xJp(k1x)Jp(k2x)dx =

{

0 si k^21 =6 k22 P^2 2 ( l2 -- -k2) Jp^2(kl) si k1 = k2

o`u k1, k2 sont des racines de J_p(kl) = 0.

Proposition 5.2.(Orthogonalitédes fonctions cylindriques)[1] Soit Fç(K^Ä_çnx) une fonction telle que

F_ç(K^Äx) = ù1Jç(K^Ä_çnx) + _{ù2Yç(KÄçnx),} ç c R.(5.28)

Si

Fç(K^Ä_çnl1) = Fç(K^Ä_çnl2) = 0 pour _l1,l2 =6 0

alors

o`u

F (K^Ä x) = R(l1,l2) _JÄ₊ V (

ç çn ç(Kçn71 çnx).

= 41,l2) = ù1 ^--1^7-77(K_ç^Ä_nl1) --1^7-77(K_ç^Ä_nl2)

J(KAl1) Jç(K^Ä_çnl2)

et les racines _KÄçn sont telles que

~~ A = ~~

Jç(K^Äçnl1) Yç(K^Äçnl1) Jç(K^Äçnl2) Yç(K^Äçnl2)

~~~~

= 0

Dans ces conditions :

l2 R l1

xFç(K;?i'x)Fç(K7tx)dx = 21 [l3 (Fç+1(Kçnl2))^2 -- l? (Fç+1(K,,nl1))^2] äij.(5.29)

äij est le symbole de Kronecker. Concernant les intégrales :

Th'eor`eme 5.1.[1]

Soit U_ç(x) une combinaison linéaire de fonctions de Bessel de premi`ere esp`ece et de seconde esp`ece, ainsi que de fonctions de Hankel. Ces fonctions d'ordre ç ayant x pour argument, alors :

pour ç c R

f x^1-çU_ç(x)dx = --x^1-çU_ç-1(x).(5.30)
R x^1+çU_ç(x)dx = x^ç+1U_ç+1(x).(5.31)

1. Premi`ere solution (c1 = d1 = 0)

P(x1, x2) = En⁸=1 Anxs1Is (ó2Kvn x1) x^v₂J_v(K_vnx2).(5.32)

ó1

En c2 la probabiliteegale a` 1.

On extrait le terme x^v₂ independant de n :

(ó2Kvn

ó1

_x-v

2 = E⁸n=1 Anc^s2Is

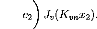
Trouvons le coefficient A_n de la serie de Fourier generalisee. Multiplions l'equation precedente par x2Jv(K_vn⁰x2) et integrant de 0 a`

d2

d2 R 0

x2 1-v Jv(Kvn^0x2)dx2 =

d2 R 0

(ó2 Kvn En^8 Anc^s2I c2) x2Jv(Kvnx2)Jv(Kvn^, x2)dx2. ó1

D'après l'orthogonalitedes fonctions de Bessel, on obtient :

d2

x₂ J_v(i

1-v _Tz

vn, x2 )dx2

cd22I,s (ó2K vn' c2) Jv+1(Ù_vn^,))² ó1

A_n^, =

2 0

c2) Jv(Kvnx2).

.(5.33)

Calculons I1 =			d2 R 0		x2 1-vJv (Kvn, x2)dx2 . dx = Kvn^, d^X2
1 = K^2-0^v vn	^Ùvn	0
	f			x^1-vJv(x)dx.

Effectuons le changement de variables suivant :

x = Kvn^,x2 = Alors

Ùvn^,x2 d2

D'après le theorème 5.1.

~ I1 = K^2-,^v 2^v-¹(v) 1 1

Ù1-, vJv-1(Ù

vn

vn

Cela on considerons que v > 0

x1-v J_v 1(x) _>

^I 2v-P(v), x ? 0.

Alors

ó2 Kvn

2v-2(v)Ùv77,v*Vs( ó1

.(5.34)

A_n =

1 - 2^v-1(v)R¹,₇7,^vJ_v-1(Ù_vn)

c2)(Jv+1(Ùvn))²

2. La deuxi`eme solution:(c1 > 0, d1 = 0)

P(x1, x2) = En=⁸ 1 Bn41x'2'Gs ( ó2Kvn x1 ) Jv(Kvnx2).(5.35)

ó1

De la màeme facon on trouve

1 - 2v-1(v)Ùvnt4-1(Ùv1n ^v)

₂G_s(^ó2Kvn

2v-2(v)Ù2-v vn câ1

₂ dv

ó1

B_n =

.(5.36)

c2)(Jv+1(Kvnd2))²

3. La troisi`eme solution:(c1 = 0, d1 > 0)

P(x1, x2) = En8=1 Anx^s14^2 Is (ó2Ke'n ó1

vn,)] . x1) Fv(KÄvnx2).(5.37)

Toujours comme precedemment:

P(x1 = c2, x2) = 1 et on extraire xâ2

2 independant de n

x2 â2 = EZ__{1 Ancs1Is} ^(ó2Ke.nc1) Fv(K^Ä_vnx2)

ó1

En multipliant cette expression par x2F_v(K^Ä,x2), et en int'egrant de

vn

d1 a` d2 et en tenant compte le fait que les fonctions cylindriques sont orthogonales, on obtient :

2 An =

d2 d1

x2 1-â2Fv(Ke'nx2)dx2 (ó 2 K vÄn A Is c2) ilân ó1

(*)

.(5.38)

avec Ëân = d2 {Fv+1(K^Ä_vnd2)}² -- di _{{Fv+1(KÄvnd1)}2} .

4. La quatri`eme solution:(c1 > 0, d1 > 0)

K

Ä

_âi (

P(x1, x2) = En^°°=1 Bnx1 x2 ⁰² Gs ó2 vn x1) F_v(K^Ä_vnx2).(5.39).

ó1

De la màeme facon on trouve ais'ement

d2 x2 1-â2 Fv(KÄvnx2)dx2 (**)

d1

_er re-Ä .(5.40).

c₂ G_s

â1 vn A

ó1 c2) ilân

2

B_n =

avec Ëân = d2 {Fv+1(K_v^Ä_nd2)}² -- di _{{Fv+1(KÄvnd1)}2} .

Remarque: Pour le calcul des int'egrales(*) et (**) en utilise le r'esultat du th'eor`eme (5.1.).

Part VI

Simulation

Dans cette partie nous présentons des programmes de simulation pour le mouvement brownien et le processus de Bessel bidimensionnels, ainsi que la probabilitéde premier passage pour des cas choisit.

1.Simulation de Mont'e-Carlo (rappel)

Soit X une variable aléatoire construite sue l'espace probabiliste (Ù, F, P). Nous pouvons déterminer la loi de X en considérant sa fonction de répartition

FX(x) = P(X),Vx E R

Soit g : R -+ R une fonction. Vous voulons estimer l'espérance de g(X):

E(g(X)).

A l'aide d'un ordinateur,nous allons réaliser une suite de tirages de la variables aléatoires X selon la loi F en utilisant un générateur de nombres pseudoaléatoires. Si Xi représente le résultat du ^ii`em tirage et que l'on effectue m tirages alors

g(X1),...g(X_n)

représentent un échantillon aléatoire simple. Supposons que

V ar(g(X)) < 00

1
m

Dans ce cas la loi forte des grands nombres nous permet de conclure que Pn i=1 g(Xi) -+ E(g(X))p.s.

lorsque

m + 00.

De plus le théorème limite central montre que la loi de

1

n 2

n

1 Pn i=1 g(Xi) - Eg(X)
V arg(X)

converge vers la loi N(0, 1).

Nous sommes donc en mesure de calculer un intervalle de confiance pour Eg(X)

[ Pn 1 i=1 g(Xi) - zá n 2

(V arg(x))1 2 >n (V arg(x) ~1 2 ] ; 1 i=1 g(Xi) + zá n n 2 n

pourvu que le nombre de trajectoires simulées soit grand.

Lorsque la variance V arg(X) n'est pas connue, on l'estime par la variance empirique.

2.Simulation d'un mouvement brownien bidimensionnel

Soit W = (W¹; W²) un mouvement brownien bidimensionnel, dont les composantes sont indépendantes.

Soit T la matrice de corrélation de dimension 2 * 2.

Nous voulons construire un mouvement brownien bidimensionnel B = (B¹; B²) tel que

Corr(Bⁱ _t, B^j_t) = ñij, Vt

o`u _ñij est l'élément de T.

3.Simulation du processus de Bessel bidimensionnel

Considérons une équation différentielle stochastique de la forme

dXt = b(t, Xt)dt + ó(t, Xt)dWt X0 = x0.

La premi`ere étape consiste a` assurer qu'il existe bien une solution a` cette équation différentielle stochastique.

Nous appliquons ensuite la méthode d'Euler :

X* 0 = x0

X* (n+1)Ät = X* nÄt + b(nÄt, X* nÄt)Ät + ó(nÄt, X* nÄt)(W * (n+1)Ät - W * nÄt)

Soit une E.D.S.

1

dXt = dWt + dt, X0 = 0.

2Xt

1

On a b(t,Xt) = , ó(t, Xt) = 1.

2Xt

Le schéma d'Euler est :

X* 0 = 0. 1 X* (n+1)Ät = X* nÄt + 2X* nÄt

Ät + (W * (n+1)Ät - W * nÄt).

Remarque:

Les programmes MATLAB sont donnés dans l'annexe.