II-2-2). La résonance de la fonction
diélectrique présente un facteur de qualité
différent selon les matériaux III-V [II-3] :
Dans la partie précédente, nous avons vu
qu~à la fréquence : 1 où il y a une forte
réflexion, où la fonction diélectrique présente une
résonance (correspond à un couplage entre la fréquence
excitateur et la fréquence de l~oscillateur de Lorentz). Cependant, le
GaAs possède une meilleure réflectivité parmi les
III-V. Ceci est bien illustré dans la figure.II-4.
qui représente la résonance de la fonction
diélectrique de différents matériaux de III-V
(GaAs, InAs, InP, InSb,&.).
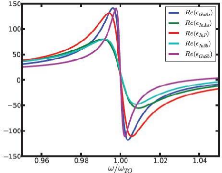
Figure.II.4. Partie réelle de la fonction
diélectrique " pour différents composés III-V [II-3].
Donc, d~après la figure.II.4, il est
clair que GaAs possède un meilleur facteur de qualité en
résonance de la fonction diélectrique, car le meilleur maximum de
" est celui associé a GaAs, et la partie réelle ' qui
tend vers les valeurs les plus négatives est celui associé a
GaAs. Ceux-ci montre que le GaAs présent une meilleure
réflectivité parmi les III-V.
Finalement, on déduit alors que la fonction
diélectrique est un outil qui nous permet de caractérisé
la réflectivité d~un matériau d~après la
présentation du leur résonance.
Cependant, et en observant la figure.II.4, on
trouve que la fonction diélectrique présente sa résonance
à une fréquence qui égale la fréquence optique
transverse TO (phonon optique transverse). Donc il est convient de
donner l~expression de la fonction diélectrique en fonction de
TO [II-2] :
Que l'on peut exprimer encore en fonction de fréquences
longitudinales LO et transverses TO [II-3] :
|
En effet :
|
R
|
2 2 æ -ö
1 2 LO 2 TO
+ ÷ (II-21)
è - - ø
j
TO
|
En donnant l'expression de la fonction (formule (II-20))
diélectriques aux limites [II-4] ( ® 0 , E ®
S) :
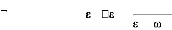
N 1e2
2
Þ
S
+
TO
0 m1
D'où :
Ne 2
1
- = 2 (II-22)
TO
0 m1
Et, en remplaçant dans l'expression de
R (formule (II-20)), on écrit :
|
|
2
|
|
|
+s - e
|
TO
|
(II-23)
|
|
R
|
2 - +
2
( j g 1 )
TO
|
Dont, dans ce formule on voit que pour un faible amortissement (
® 0 avec g ), la
TO
1
2
fonction diélectrique R va être
nulle à une fréquence donné par [II-4] :
æ ö
s
' = ÷ 03TO (II-24)
è ø
Qui peut être traduite par la relation de
Lyddane-Sachs-Teller (LST) en posant ' =
LO
( LO est la fréquence optique
longitudinale) :
æö
s
LO = ÷coTO (II-25) c-à-d
:
è ø
1
2
2
(II-26)
LO = s
2
TO
Cependant, en substituant dans l'expression de la fonction
diélectrique (formule (II-23)), nous aurons l'expression de la fonction
diélectrique d'un semi-conducteur tient compte des modes de vibrations
longitudinaux LO et transverses TO
donnée par (formule (II-21)) :
|
2 2
æ - ö
= 1 2 LO 2 TO
+
R ÷
è - - ø
j
TO
avec :
|
g
|
|
|
TO
|
Cependant, la fonction diélectrique s~annule pour la
fréquence LO associée au mode
longitudinal, par contre la fréquence transverse
TO présente un pole de la fonction
diélectrique
[II-2], tels que si la fréquence du rayonnement
excitateur est comprise entre ces deux
fréquences
TO et LO ( TO p p
LO) limitant la bande Reststrahlen, la
réflexion sera très
forte. Ceci que nous allons discuter dans la partie suivante.
| 


