3.3.1.6 Choix du meilleur ou des modèles entre
l'analyse factorielle discriminante et celle bayésienne
Tableau 21 : Comparaison entre les
modèles issus de l'analyse factorielle discriminante et celle
bayésienne
|
Modèles
|
|
Nombre de mal classés
|
Fonction discriminante (Analyse factorielle discriminante)
|
Fonctions discriminantes
linéaires de Fisher (Analyse discriminante
bayésienne)
|
|
Pauvres
|
111
|
422
|
|
Non pauvres
|
111
|
311
|
|
Total
|
222
|
733
|
|
Taux d'erreur de classement
|
2,9%
|
9,7%
|
Source : Calcul de l'auteur sur les données de l'ELEP 2007
sous SPSS
Au vu de ces résultats, le taux d'erreur de classement est
:
Pour le modèle de la fonction discriminante, il est de
2,9% (222/7552)*100.
Pour les deux modèles des fonctions discriminantes
linéaires de Fisher, il est de 9,7% (733/7552)*100.
Le choix du meilleur modèle ou des modèles doit
porter sur celui ou ceux qui a ou ont le plus faible taux d'erreur de
classement. Donc, notre choix va porter sur le modèle de la fonction
discriminante de l'analyse factorielle discriminante, car il a le plus faible
taux d'erreur soit 2,9%.
Le modèle retenu est le suivant :
F = 1,222*Rural +0,489*Indépendant agricole
+0,112*Aucun niveau d'instruction - 0,446*Supérieur
+0,160*Salarié public +0,212*Indépendant non agricole + 0,003*Age
chef du ménage -0,331*Technique professionnelle -0,103*marié
monogame - 2,212*Conakry +1,179*N'Zérékoré +1,173*Kankan
+1,115*Faranah + 0,297*Labé + 0,108*Kindia -1,148
Le modèle que nous avons construit, nous a permis de
constater que la pauvreté des ménages est fonction du milieu de
résidence (rural), du groupe socio-économique du chef de
ménage
49
(indépendant agricole, indépendant non agricole et
salarié du secteur public), du niveau d'instruction du chef de
ménage (aucun niveau d'instruction, technique professionnelle et
supérieur), du statut matrimonial du chef de ménage (marié
monogame), de l'âge du chef de ménage), mais également de
la région d'habitation (Conakry, N'Zérékoré,
Kankan, Faranah, Labé et Kindia).
C'est ce modèle qui permettra de classer les
ménages de sorte que, connaissant les caractéristiques d'un
ménage donné, il soit possible de les classer soit dans la
catégorie des pauvres, soit dans celle des non pauvres.
3.3.1.7 Adéquation du modèle de classement
retenu
Dans le but de construire le modèle de
prédiction, il est d'un intérêt de faire un examen de son
pouvoir discriminant. Cet examen se fait par calcul de l'aire au-dessous de la
courbe ROC (Receiver Operating Characteristic) ou courbe de
caractéristiques d'efficacité. Cette courbe permet
d'étudier les variations de la spécificité et de la
sensibilité d'un test pour différentes valeurs du seuil de
discrimination.
La courbe de ROC est utilisée dans les méthodes
de classement ne mettant en oeuvre qu'une seule variable à deux
modalités et utilisées pour la classification des sujets. Elle
est avant tout définie pour les problèmes à deux classes
(les positifs et les négatifs), elle indique la capacité du
classifieur à placer les positifs devant les négatifs, sa
construction s'appuie donc sur les probabilités d'être positif
fournies par les classifieurs. Il n'est pas nécessaire que ce soit
réellement une probabilité, une valeur quelconque dite «
score » permettant d'ordonner les individus suffit amplement.
Dans notre exemple, sur l'axe des abscisses, on porte la variable
1- spécificité donnant l'effectif (en pourcentage) de non pauvres
parmi les pauvres, sur l'axe des ordonnées, on place la
sensibilité égale à l'effectif (en pourcentage) de vrais
pauvres parmi les non pauvres. Si Se et Sp désignent respectivement la
sensibilité et la spécificité du test, nous avons :
y' Se=Pr(le test décide que l'individu est pauvre sachant
qu'il est effectivement pauvre) ;
y' Sp=Pr(le test décide que l'individu n'est pas pauvre
sachant qu'il n'est effectivement
pas pauvre).
La surface sous cette courbe nous permet d'évaluer la
précision du modèle pour discriminer les ménages pauvres
des ménages non pauvres.
Mémoire de fin d'études
50
On retiendra comme règle:
- Si aire ROC = 0.5 il n'y a pas de discrimination ;
- Si 0.5 < aire ROC < 0.7 la discrimination est
insuffisante ; - Si 0.7 < aire ROC < 0.8 la discrimination est acceptable
; - Si 0.8 < aire ROC < 0.9 la discrimination est excellente ; - Si aire
ROC = 0.9 la discrimination est exceptionnelle.
Graphique 03 : Courbe de ROC du modèle de
classement retenu
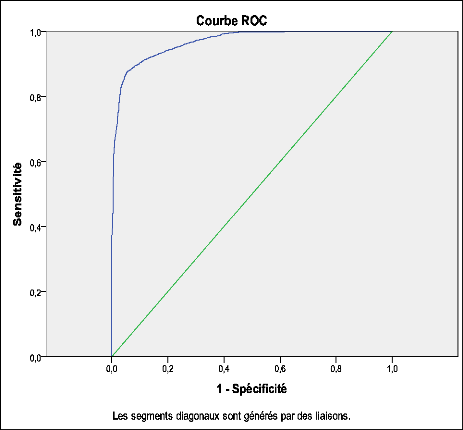
Source : Calcul de l'auteur sur les données de l'ELEP 2007
sous SPSS
Un test avec un fort pouvoir discriminateur occupera la partie
supérieure gauche du graphique. Un test avec un pouvoir discriminant
moins puissant montrera une courbe ROC qui s'aplatira vers la première
diagonale du graphique.
Dans notre cas, nous avons un test qui a un fort pouvoir
discriminateur.
Mémoire de fin d'études
51
Tableau 22 : Aire sous la courbe de ROC du
modèle de classement retenu
|
Zone sous la courbe
|
|
|
Variable(s) de résultats tests: Probabilité
d'appartenance au groupe pour l'analyse
|
|
|
Zone
|
Erreur Standard.a
|
Signification
asymptotiqueb
|
Intervalle de confiance 95 % asymptotique
|
|
|
Borne inférieure
|
Borne supérieure
|
|
0,966
|
0,002
|
0,000
|
0,963
|
|
0,970
|
Source : Calcul de l'auteur sur les données de l'ELEP 2007
sous SPSS
La ou les variables de résultats tests :
Probabilité d'appartenance au groupe pour l'analyse comporte au moins
une liaison entre le groupe d'état réel positif et le groupe
d'état réel négatif. Les statistiques peuvent être
déformées.
a. Dans l'hypothèse non-paramétrique
b. Hypothèse nulle / : zone vraie = 0.5
L'aire sous la courbe (AUC) indique la probabilité pour
que la fonction SCORE place un positif devant un négatif (dans le
meilleur des cas AUC = 1). Il existe une valeur seuil, si l'on classe les
individus au hasard, l'AUC sera égal à 0.5.
Dans notre exemple, nous remarquons que la valeur de l'aire sous
la courbe est très importante. Pour ce modèle, l'aire sur la
courbe ROC vaut 96,6%, ce qui traduit un pouvoir discriminant exceptionnel.
Ceci démontre encore une fois que le modèle retenu
est d'une excellente qualité.
Mémoire de fin d'études
52
Mémoire de fin d'études
| 


