La Volatilité et la
Saisonnalité
1. Volatilité
Il existe deux types de volatilité : la
volatilité historique et la volatilité implicite.
· Volatilité
historique : elle mesure les variations des cours du
sous-jacent par le calcul de l'écart
type sur un nombre assez faible de séances (souvent 10).
· Volatilité
implicite : mesure les anticipations de
variation de cours du sous-jacent.
Pour utiliser la volatilité on dit qu'une option
est surcotée si la volatilité implicite supérieure
à la volatilité historique, elle est sous cotée si la
volatilité implicite inférieure à la
volatilité historique.
1.1 Définition
C'est une valeur qui mesure la propension d'un actif (action,
taux d'intérêt,...) à varier significativement à la
hausse ou à la baisse. Plus cet actif à tendance à varier
fortement sur une courte période de temps, plus cet actif est dit
volatile.
Autrement dit que la volatilité est une mesure de
l'instabilité du cours d'un actif financier. Elle sert de
paramètre de quantification du risque de rendement et de prix
d'un actif financier.
1.2 Calcul de la volatilité
tQ
Volatilité = std log
t - 1Q
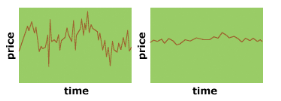
Elle dépend des séries chronologiques de prix de
deux capitaux hypothétiques. Nous pouvons penser à la
série des prix du côté gauche comme plus risqué.
Nous disons qu'il est l'"plus volatil" des deux. Nous formalisons ceci en
définissant la volatilité comme suit :
t-2Q, t-1Q, tQ, t+1Q Laissé soyez un
processus stochastique. Ses limites peuvent représenter des prix,
valeurs, taux de change, taux d'intérêt accumulés. La
volatilité du processus au T-1 de temps est définie comme
l'écart type du retour du temps t. Typiquement, des retours de notation
sont employés, ainsi la définition devient.
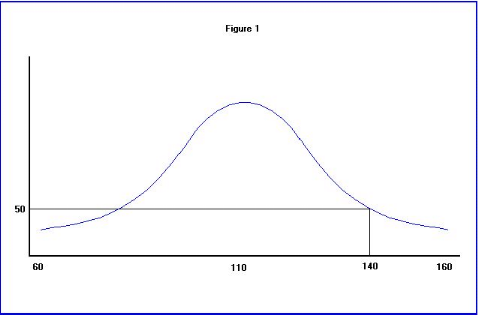
La volatilité et les statistiques peuvent probablement
mieux être décrites à titre d'exemple. La figure 1
représente un graphique des résultats d'un essai de Q.I. pour
1000 personnes. L'axe de X lit de 60 à 160 et représente la gamme
des points de Q.I. pour les personnes impliquées dans l'essai. L'axe de
Y représente le nombre de personnes avec un Q.I. particulier (comme
mesuré par l'axe de X).
La plupart des personnes ont marqué au milieu de la
gamme avec l'IQS près de l'identifier 110 par peu de gens aux
extrémités supérieures et inférieures de gamme. Par
exemple, une lecture d'axe de Y de 50 avec le niveau d'axe de X de 140
indiquerait qu'il y avait 50 personnes dans l'échantillon avec un Q.I.
de 140.
NB : La courbe sur le
schéma 1 est symétrique avec une crête au milieu
aplatissant dehors aux queues des deux côtés. Ce type de courbe
s'appelle une courbe de distribution normale. Des courbes de distribution
normale sont employées pour mesurer une série
d'événements indépendants ou apparemment
aléatoires. Une courbe de distribution normale peut être
mesurée par deux nombres, son moyen et son écart type. Le moyen
est la moyenne de l'échantillon et est représenté par la
crête de la courbe. L'écart type est employé pour mesurer
la probabilité d'un certain événement se produisant dans
la courbe de distribution normale.
La théorie statistique déclare cela
approximativement :
- 68% de toutes les occurrences sera dans + 1 écart type
du moyen ;
- 95% de toutes les occurrences sera dans + 2 écarts type
du moyen ;
- 99% de toutes les occurrences sera dans + 3 écarts type
du moyen.
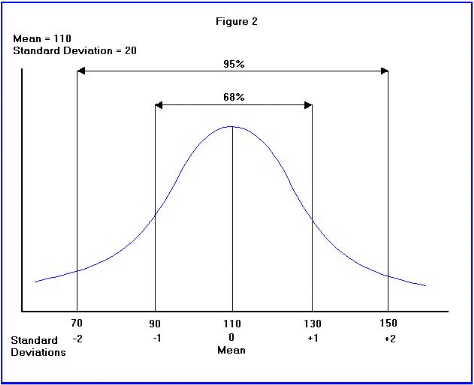
La figure en face représente la même courbe de
distribution normale que la figure précédente, toutefois un moyen
de 110 et un écart type de 20 ont été inclus dans le
diagramme. Si vous vouliez savoir la probabilité d'une personne ayant un
Q.I. 150 plus grands que vous pourriez calculer la probabilité de ceci
se produisant comme suit :
150 est plus de 2 écarts type loin du moyen.
Nous savons que 2 écarts type du moyen entoure 95% de
toutes les occurrences, dans ce cas-ci les gens avec l'IQS de 70 à
150.
Cependant ceci signifie également qu'il y a une chance
de 5% d'une personne ayant un Q.I. plus de 2 écarts type du moyen, moins
de 70 ou 150 plus grands que.
Puisque le 3ème écart type prend dans les deux
extrémités de la courbe de distribution normale, la
possibilité d'une personne ayant un Q.I. 150 plus grands qu'est
moitié de 5%, c.-à-d. 2 le ½ %.
| 


