3.2.2 Implémentation des algorithmes et tracé
des trajectoires sous Matlab
Nous avons implémenté avec Matlab [13] les
fonctions des différentes méthodes correspondant aux deux
approches dont la poursuite cyclique et le rapetissement de courbe. Dans
chacune d'elles, nous avons tracé des graphes affichant les
trajectoires, effectuées par un groupe d'agents, pour vérifier
leur convergence au point centre de gravité.
Poursuite cyclique
Pour effectuer cette stratégie, les agents évoluent
selon le système ci-dessous avec la matrice A qui change suivant la
méthode.
z_ =Az (3.1)
Remarque 3.1 Il existe une deuxième méthode pour la
résolution du système 3.1, qui consiste à trouver
itérativement les positions z telles que :
z = expm(At ).z0
Où expm(A) est la matrice exponentielle de A, et est
calculée en utilisant la formule suivante :
expm(A) = V diag(exp(diag(D))) V ~1
Avec D : un vecteur constitué de l'ensemble des valeurs
propres, et V: la matrice des vecteurs propres correspondant.
Ceci revient à calculer les valeurs et les vecteurs
propres d'une matrice de dimension n, et donc de résoudre une
équation et un système d'équation de l'ordre n. Ce dernier
pouvant être très grand, il devient très difficile de
résoudre le système. En utilisant matlab, ceci fut simple
à implémenter car la fonction expm est prédéfinie.
Mais pour programmer la classe Java qui le résout, l'exécution de
la fonction aura une très forte complexité dans l'utilisation des
ressources (temps et espace mémoire). C'est pour cela que nous avons
employé une méthode plus simple qui est celle de Runge Kutta
d'ordre 4.
Poursuite cyclique traditionnelle Dans cette méthode, la
matrice A de la formule 3.1 est une matrice circulante de la forme : A1 =
circ(-1 , 1,0,.. . , 0), et l'algorithme est le suivant :
Algorithme 3.2
Début
% n est le nombre d'agents
% z est un tableau contenant les positions des agents % zn est le
centre des agents
A1 = zero (n); % une matrice nulle de dimension n
Pour i = 0 à n - 1 % Construire la matrice circulante
j
= (i+1) mod n;
A1(i,i) = -1;
A1(i,j) = 1;
fin pour
zn = mean(z) % la moyenne du tableau z
h = 0.1;
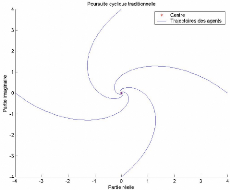
FIG. 3-1 - 4 agents dans une poursuite cyclique
traditionnelle
Tant que (z =6 zn) % les agents ne sont pas au centre
wi = Al * z;
w2=A1 *(z+ (h/6) *wl); w3=Ai *(z+ (h/6) *w2); w4=Al
*(z+h*w3);
z = z +((h/6) * (w1+2*w2+2*w3+w4));
fin tant que
fin.
Implémentant plus formellement cet algorithme sous matlab,
et traçant un plot des positions "z", nous obtenons la courbe dans la
figure 3-1 pour n = 4:
Poursuite cyclique hiérarchique Dans ce schéma, la
matrice AL (L étant le nombre de couches) est circulante à blocs
et est obtenue d'une manière récursive à partir de la
formule 2.15.
L'algorithme de la poursuite cyclique hiérarchique est le
même que celui de la traditionnelle avec une différence dans le
calcul de la matrice A.
Algorithme 3.3 Début ...
% L est le nombre de couches.
% ni est le nombre d'agents de la première couche.
nm = L pn;
Am = circulante(L,n,n1,nm); zn = mean(z);
...
fin.
Et voici un pseudo code de la fonction circulante(L,n,n1,nm) :
Code 3.1 Fonction circulante(m,n,n1,nm)
début
si (m = 1) % la matrice A1
A = zero(n1); %la matrice nulle
pour i=0 à n1-1
j = (i+1) mod n;
A1(i,i) = -1;
A1(i,j) = 1;
fin pour
sinon
size = nmm~1 ;
Id = eye(size); % La matrice identité de dimension size
mat=circulante(m-1,n,n1,nm) - Id % La récursivité pour calculer
Am-1
size = nmm;
A =zeros(size2, size2);
pour cpt=0 à ((size2/size)-1)
pour i=0 à size-1
pour j=0 à size-1
k = i+size*cpt;
l =j+size*cpt;
r = (l + size) mod size2 ;
A(k,l)=mat(i,j); % Am-1 - I
A(k,r)=Id(i,j); % I
fin pour
fin pour
fin pour
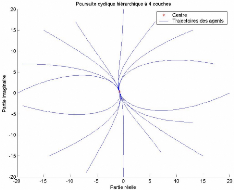
FIG. 3-2 - 16 agents dans une poursuite cyclique
hiérarchique à 4 couches
fin.
Sous Matlab, nous avons obtenu la courbe dans la figure 3-2
traçant les trajectoires des agents dans une poursuite
hiérarchique à L = 4 couches, et n = 16 agents.
Poursuite cyclique à L liens Ce schéma est aussi
résolu avec l'équation 3.1, et la matrice correspondante AL est
calculée à partir de la formule 2.17. L'algorithme qui
implémentera cette méthode sera le même que la
méthode précédente, et un pseudo code sous matlab
décrivant la fonction de calcul de la matrice AL est la suivant :
Code 3.2
Début
A=zeros(n,n); % Initialisation de la matrice
pour k=0 à n-1
r = (k+1) mod n;
A (k, k) =-L ;
pour cpt=0 à L-1
r = (r+cpt) mod n;
A(k,r2)=1;
fin pour
fin pour
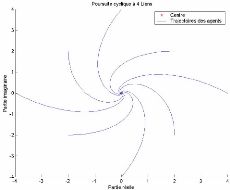
FIG. 3-3 - 8 agents dans une poursuite cyclique à 4
liens
A=(1/L) *A Fin.
Le graphe traçant les trajectoires d'un groupe de 8 agents
effectuant une poursuite cyclique à 4 liens est dans la figure 3-3.
Rapetissement de polygone
Dans cette approche, à chaque instant "t", la position
d'un agent est calculée à partir des positions
précédentes de ses deux agents voisins. L'algorithme suivant
trace les trajectoires des agents utilisant la technique de la courbure de
Menger-Melnikov ou celle du schéma linéaire. Il est le même
pour les deux méthodes, la différence réside dans le
calcul de la fonction C de la formule 3.2. La résolution se fait
toujours en utilisant la méthode de Runge Kutta.
z_ = C(zi_1,zi,zi+1) (3.2)
Algorithme 3.4
De but
% n est le nombre d'agents
% z est un tableau contenant les positions des agents à
l'instant t % zprec est le tableau qui contient les positions à
l'instant t-1
% zn est le centre des agents
zn = mean(z) % la moyenne du tableau z
h = 0.1;
Tant que (toutes les positions =6 centre)
pour chaque agent
zprec(i) = z(i);
w1 = Ci( zprec(j), zprec(i), zprec(k));
w = Ci( zprec(j)+(h/ )*w1, zprec(i)+(h/ )*w1, zprec(k)+(h/
)*w1);
w3 = Ci(zprec(j) + (h/ ) *w , zprec(i) + (h/ ) *w ,zprec(k) +(h/
) *w );
w4 = Ci(zprec(j)+h*w3, zprec(i)+h *w3,zprec(k)+h*w3);
z(i) = zprec(i) + ((h/6) * (w1 + *w + *w3+w4));
finPour
fin tant que
fin.
Rapetissement par Menger-melnikov Pour cette méthode,
comme nous avons vu au chapitre précédent la fonction C est
calculée comme suit :
(zi_1 - zi - zi+1 - zi ) 1
ci(zi_1, zi, zi+1) = zi_1 - zi zi+1 - zi zi_1 -
zi+1
Nous traçons alors le graphe qui décrit le
rapetissement du polygone formé par les agents, ainsi que les
trajectoires accomplies par les agents lors de leur convergence au centre. Voir
la figure 3-4
Schéma linéaire Dans ce cas, la fonction C est
définie comme suit, et les trajectoires, tracées par 16 agents
mobiles effectuant un rapetissement de polygone, sont dessinées dans la
figure 3-5:
1 1
ci(zi_1,zi,zi+1) = 2(zi+1 -zi)+
2(zi_1 -zi)
Remarque 3.2 Les graphes seront commentés au chapitre
suivant, où nous donnerons tous les résultats déduits sous
Matlab, en parallèle avec ceux obtenus par la simulation.
| 


