Stratégie de rendez-vous dans les systèmes multi-agents

Table des matières

Introduction générale 1 Le problème de la stratégie de Rendez-vous			1 3
	1.1	Introduction	3
	1.2	Agents et Systèmes multi-agents	3
		1.2.1 Définitions	3
		1.2.2 Architectures des SMA	5
		1.2.3 Classification des agents	7
		1.2.4 Domaines d'application des SMA	9
		1.2.5 Quelques exemples de SMA	9
	1.3	SMA et robots mobiles	11
		1.3.1 Définitions	11
		1.3.2 Application des SMA aux robots mobiles	12
		1.3.3 Exemples de SMA réalisés en robotique	12
	1.4	Stratégie de Rendez-vous des SMA	13
		1.4.1 Situation du problème	13
		1.4.2 Définition de la stratégie	13
		1.4.3 Exemples d'application de la stratégie	14
		1.4.4 Les différentes approches adoptées	14
	1.5	Conclusion	14
2	Différentes approches de la stratégie de rendez-vous		15
	2.1	Introduction	15
	2.2	La poursuite cyclique	15
		2.2.1 Préalables mathématiques	16
		2.2.2 Poursuite cyclique traditionnelle	19

2.2.3 Poursuite cyclique hiérarchique 20

2.2.4 Poursuite cyclique à L liens 24

2.2.5 Comparaison et taux de convergence 25

2.3 Le rapetissement de polygone 29

2.3.1 Préalables mathématiques 30

2.3.2 Rapetissement par la courbure de Menger-Melnikov 33

2.3.3 Le schéma linéaire 35

2.3.4 Remarques 35

2.4 Conclusion 35

3 Mise en oeuvre de la simulation 37

3.1 Introduction 37

3.2 Vérification et implémentation des algorithmes sous Matlab 38

3.2.1 Résolution de la dynamique du système 38

3.2.2 Implémentation des algorithmes et tracé des trajectoires sous Matlab 39

3.3 Mise en oeuvre de la simulation 45

3.3.1 Cahier de charge du simulateur 47

3.3.2 Conception du simulateur 47

3.3.3 Réalisation de l'interface graphique 53

3.4 Conclusion 56

4 Résultats et discussions 57

4.1 Résultats obtenus sous Matlab 57

4.1.1 Comparaison entre les méthodes 57

4.1.2 Mise à l'échelle du nombre de couches dans un schéma hiérarchique 59

4.1.3 Mise à l'échelle du nombre de liens dans un schéma à L liens 59

4.2 Résultats de la simulation 59

4.2.1 Poursuite cyclique 61

4.2.2 Rapetissement de polygone 62

4.2.3 Remarques 63

4.3 Conclusion 63

Table des figures

1-1	Interaction d'un agent avec son environnement	4
1-2	Architecture d'un SMA à contrôle centralisé	6
1-3	Architecture d'un SMA à contrôle distribué	6
1-4	Structure d'un agent réactif dans un environnement multi-agents	7
1-5	Structure d'un agent cognitif dans un environnement multi-agents	8
2-1	la structure d'une poursuite cyclique traditionnelle à 4 agents	19
2-2	Structure d'un schéma hiérarchique à 2 couches (9 agents, 3 groupes)	22
2-3	Trois couches d'hiérarchie dans une poursuite cyclique	23
2-4	Structure d'une poursuite cyclique de 5 agents à 2 liens	25
2-5	La dynamique du rapetissement de courbe	32
2-6	Rapetissement de polygone	33
2-7	Le cercle circonscrit de 3 points de la courbe	34
3-1	4 agents dans une poursuite cyclique traditionnelle	41
3-2	16 agents dans une poursuite cyclique hiérarchique à 4 couches	43
3-3	8 agents dans une poursuite cyclique à 4 liens	44
3-4	Rapetissement par Menger-Melnikov d'un polygone formé par 16 agents	46
3-5	Rapetissement par le Schéma linéaire d'un groupe de 16 agents	46
3-6	Diagramme de classes	49
3-7	Diagramme de séquences	54
3-8	Interface principale de la simulation	55
3-9	Rapport des résultats	56
4-1	Les 3 méthodes de la poursuite cyclique d'un groupe de 16 agents	58
4-2	Trajectoires des deux méthodes du rapetissement de polygone	59
4-3	La poursuite cyclique hiérarchique de 16 agents en fonction du nombre de couches. . .	60

4-4 La poursuite cyclique à 4, 8 ou 12 liens 60

4-5 Le comportement observé des agents avec la méthode de Menger-Melnikov 62

Introduction générale

Parmi les domaines d'application de la robotique, nous trouvons les missions de sauvetage où la présence de l'homme est menacée et telles que des robots sauveteurs doivent se réunir à un lieu donné pour effectuer cette mission au même moment. Plusieurs stratégies sont nécessaires pour effectuer une navigation fiable de robots mobiles dans un environnement contraint, l'une d'elles est la convergence à un point de rendez-vous.

Dans une telle situation, on cherche à concevoir une stratégie de rendez-vous d'un groupe de robots mobiles autonomes et homogènes, formant un système multi-agents. Dans ce mémoire, ce problème a été étudié et les solutions proposées dans la littérature notamment par Stephen L. Smith[1], ont été testées. Les travaux de Smith s'intéressent au développement d'algorithmes pour l'allocation de tâches dans des groupes de robots mobiles.

Inspirés par ses travaux et par sa thèse de master sur les stratégies de rendez-vous et de stabilisation de formations, nous allons implémenter deux approches de la stratégie de rendez-vous dont la poursuite cyclique et le rapetissement de courbe.

Notre travail se compose de quatre chapitres. Le premier représente une synthèse bibliographique sur les systèmes multi-agents appliqués dans le domaine de la robotique et à la stratégie de rendez- vous.

Au second chapitre, une description analytique approfondie de notre système et des différentes solutions proposées sera établie. Le système est composé de n agents se situant dans un plan complexe, chaque agent peut détecter les positions de certains des autres agents, selon la méthode employée. Un agent considéré comme leader doit initialiser tous les agents avec les informations nécessaires à l'accomplissement de la stratégie. Un rapport entre les taux de convergence des différentes méthodes est calculé pour comparer entre elles.

Au troisième chapitre, une mise en oeuvre des solutions proposées au chapitre 2 sera réalisée. Dans un premier temps, nous allons vérifier la validité et la convergence des algorithmes sous matlab, et tracer les trajectoires effectuées par les agents. Ensuite, une interface graphique sera réalisée, permettant de simuler les différentes approches de cette stratégie, visualiser le comportement des

agents et calculer certaines valeurs d'évaluation.

Finalement, nous discuterons les résultats obtenus par la simulation et présenterons les avantages et les inconvénients de chaque méthode, ainsi que les éventuelles difficultés rencontrées dans l'implémentation des algorithmes.

Chapitre 1

Le problème de la stratégie de

Rendez-vous

1.1 Introduction

Dans ce chapitre, le problème de rendez-vous est présenté où un ensemble d'agents mobiles réalise une convergence à un point commun. Pour cela, nous commencerons par présenter un aperçu sur les systèmes multi-agents, leur application aux robots mobiles et plus précisément à la stratégie de rendez-vous. Les différentes approches présentées dans la thèse de Stephen L. Smith [1] seront étudiées dans le chapitre 2.

1.2 Agents et Systèmes multi-agents

1.2.1 Définitions
· Agent

Un agent est une entité (physique ou abstraite) caractérisée par le fait qu'elle est autonome dans la prise de décision, par ses connaissances sur elle même et sur les autres, et par sa capacité d'agir.

Ce peut-être un processus (en gestion des processus dans les systèmes d'exploitation), un robot (dans un environnement industriel), un être humain (en sociologie), etc.

Pour Weiss (1999), un agent est une "entité computationnelle", comme un programme informatique ou un robot, qui peut être vue comme percevant et agissant de façon autonome sur son environnement. voir figure 1-1

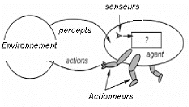
FIG. 1-1 - Interaction d'un agent avec son environnement

Caractéristiques d'un agent:

- un agent est une entité autonome mais fortement dépendante des autres.

- un agent communique à l'aide de messages, ou par partage d'informations. - un agent est autonome, il peut refuser de faire ce qu'on lui dit de faire.

- les agents peuvent être spécialisés: un agent ne sait pas faire beaucoup de choses mais

ce qu'il sait faire, il le fait vite et bien et le met en commun avec les autres agents.

· Système multi-agents

Un système multi-agents (SMA) est constitué d'un ensemble de processus informatiques se déroulant en parallèle, donc de plusieurs agents vivant au même moment, partageant des ressources communes et communicant entre eux.

Le point clé des SMA réside dans la formalisation de la coordination entre les agents.

Partant de la définition que donne Ferber(1995) [2] d'un agent logiciel, on peut définir cette entité comme un système informatique situé dans un environnement, capable de mener de manière autonome des actions sur cet environnement en vue d'accomplir ses objectifs, possédant en plus les propriétés de :

Réactivité : il perçoit des stimuli provenant de son environnement et réagit en fonction de ceux-ci. Proactivité : il est mû par un certain nombre d'objectifs qui guident ses actions.

Sociabilité : il communique avec d'autres agents ou des humains et, peut se trouver engagé dans des transactions sociales (négocier ou coopérer pour résoudre un problème) afin de remplir ses objectifs.

On parle ainsi d'intelligence artificielle distribuée.

L'une des grandes sources d'inspiration pour les systèmes multi-agents a été l'étude des comportements sociaux de certaines familles d'insectes. Dans ce domaine, on se référera utilement aux articles Intelligence collective et Intelligence distribuée.

Les SMA peuvent être vus comme la rencontre de divers domaines :

· l'intelligence artificielle pour les aspects prise de décision de l'agent.

· l'intelligence artificielle distribuée pour la distribution de l'exécution.

· les systèmes distribués pour les interactions entre agents.

· le génie logiciel pour l'approche agents et l'évolution vers des composants logiciels de plus en plus autonomes.

Les SMA peuvent être partagés en deux types d'architectures [3], en fonction du type de contrôle adopté :

SMA à contrôle centralisé ou a base de tableau noir

Composé de trois éléments :

- Les connaissances représentées par les agents.

- Le tableau noir: qui est une zone de travail commune, dévolue à la transition d'informations entre les différents agents. Chacun peut venir le consulter à sa guise, y prélever et y déposer des objets qu'il peut également modifier. Le tableau structure la modélisation du domaine d'application comme l'espace des hypothèses et des solutions.

- Le mécanisme de contrôle : concerne les contraintes sur les relations entre les conversations des protocoles qui régissent le système, et au quels l'agent peut participer simultanément ou successivement.

Le SMA à contrôle centralisé possède en outre les propriétés suivantes :

- Pas de communication directe entre les agents.

- Interaction via le partage d'un même espace de travail qui est le blackboard. - Mal adapté aux SMA large échelle.

SMA a contrôle distribué

- Une distribution totale des connaissances et du contrôle.

- Caractéristiques :

· Traitement local.

· Communication entre agents par envoi de messages.

- Le langage d'Acteur est la technique la plus utilisée pour la mise en oeuvre de ce type

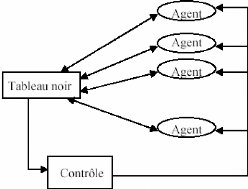
FIG. 1-2 - Architecture d'un SMA à contrôle centralisé

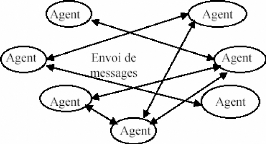
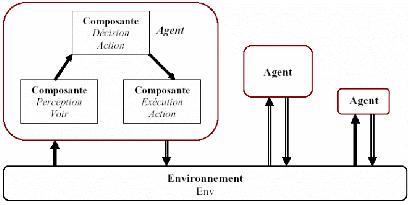
FIG. 1-4 - Structure d'un agent réactif dans un environnement multi-agents

d'architecture. Un Acteur regroupe au sein d'une même entité un ensemble de connaissances : les accointances, un script.

1.2.3 Classification des agents

Les experts des systèmes multi-agents ont classifié ces derniers (agents) en deux grandes catégories selon un critère essentiel qui est la représentation de son environnement, et sont donc les agents réactifs et les agents cognitifs, et les systèmes dits hybrides.

Agents réactifs

On parle ici de système intelligent d'agents. Les agents sont simples et ne possèdent pas une représentation de leur environnement, ni de mémoire, ce qui les prive d'apprentissage et de toutes anticipations aux évènements. Ils sont caractérisés par l'absence de structures organisationnelles initiales prédéfinies, d'où les agents agissent naturellement au moment où l'action est nécessaire. Leur comportement est de type «stimuli - réponses».Voir figure 1-4

Les SMA dotés d'agents réactifs possèdent généralement un grand nombre d'agents. Le comportement de groupe est impressionnant lorsqu'il s'agit de coordonner certaines actions, telles que leur déplacement.

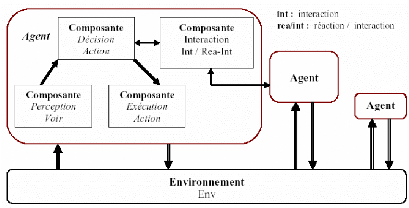
FIG. 1-5 - Structure d'un agent cognitif dans un environnement multi-agents

Agents cognitifs

On parle ici de système d'agents intelligents. Les agents cognitifs sont plus évolués, résultats des recherches menées dans le domaine de l'intelligence artificielle. Ils possèdent une représentation globale de leur environnement et des agents avec lesquels ils communiquent, ils tiennent aussi compte de leurs actions antécédentes. Chaque agent possède une base de connaissances comprenant l'ensemble des informations nécessaires à l'accomplissement de sa tâche, ainsi qu'à l'interaction avec l'environnement et les autres agents. Voir figure 1-5

Les SMA constitués d'agents cognitifs compte un petit nombre d'agents «intelligents», exigent des ressources plus importantes que les agents réactifs, et permettent de résoudre des problèmes plus complexes.

Agents hybrides

Ce type d'architecture combine les agents réactifs et cognitifs, qui sont généralement distribués sur plusieurs niveaux ou couches. La couche de haut niveau, délibérative, rassemble des agents purement cognitifs, s'occupe du raisonnement et de la prise de décision du système. La couche de bas niveau ne rassemble que des agents réactifs qui exécutent généralement des tâches élémentaires sous les ordres de la couche supérieure ou par leurs propre initiative. La (les) couches intermédiaires, peuvent regrouper les deux types d'agent (réactifs et cognitifs), le nombre de couches intermédiaires dépend du modèle du système à concevoir.

1.2.4 Domaines d'application des SMA

On distingue généralement 3 types d'utilisation des systèmes multi-agents :

La simulation ou la modélisation de phénomènes complexes

Où on utilise les SMA pour simuler des interactions existantes entre agents autonomes. Le but est de déterminer l'évolution de ce système afin de prévoir l'organisation finale. Ce qui importe c'est le comportement d'ensemble et non pas le comportement individuel. L'autonomie permet ici de simuler le comportement exact d'une entité.

La première simulation utilisant les SMA, et qui d'ailleurs fut la source d'inspiration de ceux-ci est le système MANTA (simulation d'une fourmilière) [4].

La résolution de problèmes et prise de décision

L'intelligence artificielle distribuée est née pour résoudre les problèmes de complexité des gros programmes de l'intelligence artificielle : l'exécution est alors distribuée, mais le contrôle reste centralisé. Contrairement aux SMA, où chaque agent possède un contrôle total sur son comportement. Pour résoudre un problème complexe, il est plus simple de concevoir des programmes relativement petits (les agents) en interaction, qu'un seul gros programme monolithique. L'autonomie permet au système de s'adapter dynamiquement aux changements imprévus qui interviennent dans l'environnement.

Exemple : minimisation d'impact pour des aménagements

La conception de programmes

Intégrer un système d'information constitué d'un ensemble d'agents organisés pour faciliter la compréhension et la décision, soit individuelle, soit collective. Contrairement à un objet, un agent peut prendre des initiatives, refuser d'obéir à une requête, se déplacer . . .

Exemple : systèmes d'aide à la négociation de projets

1.2.5 Quelques exemples de SMA

Les systèmes multi-agents associés à l'intelligence artificielle représentent actuellement un grand domaine d'application et de recherche. Plusieurs systèmes ont été développés, nous présenterons ici quelques uns tels que :

· Le système MANTA [4] : ce système illustre parfaitement l'intérêt de la modélisation multiagents de type réactif. Il modélise la constitution d'une fourmilière mature à partir d'une ou

plusieurs reines, étudie la capacité d'adaptation d'une telle colonie, le mécanisme de polyéthisme(division du travail), et la spécialisation des ouvrières.

Cette simulation avait vérifié le fait qu'une société d'agents peut bien survivre et s'organiser en
se passant de tout système de contrôle centralisé et d'une quelconque organisation hiérarchique.

· Le comportement de meute : les agents réactifs se montrent capables d'évoluer parfaitement en groupe tout en s'évitant mutuellement, constituant par là une meute aux comportements très souples. Le premier à s'être intéressé à ce comportement est Craig Reynolds (1987) [5], il a créé des créatures appelées "Boïds", des agents réactifs capables d'interagir pour réaliser un comportement semblable à un vol d'oiseaux migrateurs, chacun des Boïds se contentant d'appliquer un ensemble de règles comportementales :

- Maintenir une distance minimale par rapport aux objets de l'environnement y compris les autres Boïds.

- Adapter sa vitesse à la moyenne de celle de ses voisins.

- Aller vers le centre de gravité de l'ensemble des Boïds voisins.

Contrairement aux oiseaux, les Boïds évoluent sans leader et sans contrôle global. Ils contournent tous ensemble un obstacle tout en restant naturellement groupés.

· les systèmes industriels distribués : où les concepteurs partent de problèmes réels existants et ils cherchent à les résoudre en se basant sur les techniques d'interaction et de coopération des systèmes multi agents.

Plusieurs systèmes ont été développés dans les domaines de la télécommunication, et de contrôle du trafic aérien.

· Applications temps réel: Les agents ont été bien évidemment appliqués au domaine des systèmes temps réel; ce dernier maintient des systèmes à contrainte souple. On voit de plus en plus des systèmes temps réel dit Hard utilisant des agents.

· Applications agents pour le commerce électronique : Le e-commerce signifie des échanges de produits qui se passent via Internet. Les sites pour les ventes aux enchères, pour les négociations entre les utilisateurs (producteurs/consommateurs), etc.

· Applications agents pour la Recherche d'Information: Une grande partie des applications de système multi-agents est dans le domaine de recherche d'information. Parmi ces nombreuses applications dans ce domaine, on peut trouver "NetSA" [6] : une architecture de système multi-agents pour la recherche d'information dans des sources hétérogènes et réparties.

Nous avons aussi les projets suivants : Phoenix (simulation de contrôle de feux de forêts); Archon (gestion de réseaux électriques); SimDelta (simulation de gestion de ressources halieutiques); Smaala (aide à la localisation d'infrastructures linéaires); Simpop (dynamiques urbaines); Swarm (simulation d'écosystèmes); Gestion de trafic aérien ...

1.3 SMA et robots mobiles

Dans ce mémoire, nous étudierons une stratégie de navigation d'un groupe d'agents (robots) autonomes, constituant ainsi un système multi-agents.

La mise au point d'un système de navigation pour un robot mobile représente un champ d'application privilégié pour valider les notions d'agents autonomes et SMA. La robotique constitue également un champ d'application fécond pour aborder l'intelligence collective.

Après quelques définitions de termes employés, nous aborderons les SMA et leur application dans le domaine de la robotique.

1.3.1 Définitions

· Robot

Il existe plusieurs définitions d'un robot, satisfaisant plusieurs domaines. La norme internationale ISO 8373 [7] a définie un robot comme étant un manipulateur universel programmable, automatiquement contrôlé, reprogrammable, ayant 3 axes ou plus, qui peut être soit fixé dans une place ou mobile dans le cas des applications industrielles automatisées.

· Robot mobile

Un robot mobile est une machine automatique qui est capable de naviguer dans un environnement, généralement non fixé à un endroit physique.

Les robots mobiles sont le centre de beaucoup de recherches courantes et presque chaque université principale possède un ou plusieurs laboratoires de recherche des robots mobiles.

· Robot autonome

Les robots autonomes sont des robots qui peuvent accomplir des tâches désirées dans des environnements contraints sans assistance humaine continue. Ils peuvent également apprendre ou gagner de nouvelles possibilités, comme ajuster les stratégies d'accomplir leurs tâche(s) ou à s'adapter aux environnements changeants.

Un degré d'autonomie élevé est souhaitable dans les domaines tels que l'exploration de l'espace, où l'acquisition de l'information est retardée et les interruptions sont inévitables.

1.3.2 Application des SMA aux robots mobiles

Ces dernières années, plusieurs équipes de recherche de robots mobiles intègrent les architectures de systèmes multi-agents dans la navigation, les stratégies de positionnement et les tâches que peut accomplir un groupe d'agents.

L'utilisation d'agents robotiques est bénéfique dans le sens où, cela permet de limiter la perte de vies humaines dans les milieux hostiles.

L'exemple d'application le plus courant est : la collaboration d'un groupe de robots mobiles et l'exploration d'un environnement contraint d'obstacles, en vue d'accomplir certaines tâches. Ce type de problèmes peut facilement être modélisé en appliquant un SMA. Vu sa complexité, le comportement global sera distribué sur les agents, et chaque robot se doit d'être autonome pour pouvoir réaliser sa tâche, s'adapter à l'environnement et réagir aux évènements inattendus.

1.3.3 Exemples de SMA réalisés en robotique

Plusieurs systèmes multi-agents ont été développés dans le domaine de la robotique, nous citerons seulement quelques uns dont le succès a attiré notre attention :

· La reprise des travaux de Reynolds (comportement de meute) par Mataric (1992 -94) [8] appliqués à des agents réactifs robotiques. Un comportement de meute est obtenu par pondération des comportements d'évitement d'obstacles, de filature de robots, d'agrégation et de dispersion. Les résultats ont été moins brillants que ceux de Reynolds, car il a remarqué que les robots s'éloignent les uns des autres, ou au contraire sont très compactés. Mais il a affecté ces problèmes à la dynamique imparfaite de la mécanique des robots ainsi qu'à la limitation de leurs capteurs.

· Le projet Mars Explorer [9] : Un projet développé par l'équipe SMAC de l'université des Sciences et Technologies de Lille, concernant le positionnement de robots mobiles. Le but est d'avoir des robots qui explorent leur environnement et le cartographient, pour qu'ils puissent se repérer et s'orienter dans un environnement inconnu préalablement.

· Robots sauveteurs: Le projet AROUND (Autonomous Robots for Observation of Urban Networks after Disasters) en partenariat avec le Vietnam, est un système d'aide à la décision et qui vise à développer des systèmes automatiques d'observation et de surveillance. Il consiste à déployer et coordonner des robots autonomes d'observations dans les zones urbaines victimes

de catastrophes.

· Et on conclue avec les recherches de Stephen L. Smith (2005) [1] dans les stratégies de robots mobiles autonomes dont la stabilisation à une formation, ou encore la stratégie de Rendez-vous qui fait l'objet de notre projet.

1.4 Stratégie de Rendez-vous des SMA

La plupart des travaux actuels en système multi-agents entraînent l'utilisation de stratégies simples de contrôle local dans le but de réaliser un ou un groupe de comportements global désiré. L'un des comportements étudiés dans ce mémoire est « la convergence d'un groupe d'agents mobiles à un point commun ».

C'est un type de problèmes de Rendez-vous appelé aussi agrément ou problème de consensus. Nous étudierons et comparerons ainsi les différentes approches et méthodes initiées par S. L. Smith pour réaliser cette stratégie.

1.4.1 Situation du problème

Notre système multi-agents est tout simplement un groupe d'agents. On impose une tâche désirée au SMA, un agent superviseur doit initialiser les agents avec les informations nécessaires à l'accomplissement de la tâche. A partir de ce moment, et jusqu'à la fin, les agents agissent sans l'intervention du superviseur. Ainsi les agents sont autonomes, et tentent d'accomplir la tâche utilisant seulement leurs informations locales.

1.4.2 Définition de la stratégie

Considérons un groupe de « n » agents réactifs numérotés de 1 jusqu'à n et situés dans un plan supposé sans obstacles. La stratégie de rendez-vous consiste à partir de positions initiales quelconques et à se réunir à un point commun au même instant, ici c'est le point centre de gravité.

Les agents ne sont pas tous dirigés dans la même direction. Chaque agent, équipé d'un senseur omnidirectionnel, de détection de positions relatives, avec une capacité de capture supérieure à la dimension de son environnement, peut sentir la position de tout autre agent.

Comme la communication est coûteuse, nous admettons que moins il existe de liens entre les agents, mieux est la solution.

1.4.3 Exemples d'application de la stratégie

La stratégie de rendez-vous des SMA, associée à d'autres stratégies et techniques de groupes de robots mobiles, peut être utilisée, par exemple, dans les cas suivants :

Les missions de sauvetages, dans des milieux hostiles comme le cas d'un incendie, où un nombre de robots mobiles sauveteurs doivent arriver au même moment, pour pouvoir effectuer cette tâche.

- La recherche d'un objet dans une zone fermée, le périmètre de cette zone est déterminé par les agents qui sont équipés par des capteurs pour détecter la pièce recherchée.

- Un groupe de robots se réunissant à un minerai, pour extraire et/ou transporter la matière extraite.

- La commande automatique de véhicules ...

1.4.4 Les différentes approches adoptées

Il y eu deux approches dans l'étude des SMA. La première fut l'utilisation de l'intelligence artificielle, et la deuxième l'utilisation de l'analyse numérique pour l'étude du comportement qui résulte de stratégies locales de contrôle. Nous utiliserons la deuxième pour résoudre le problème de rendez-vous.

Smith a introduit à son tour deux approches pour la réalisation de cette stratégie, dont : la poursuite cyclique et le rapetissement de courbe.

Dans chacune de ces approches, il a présenté des méthodes possédant chacune des avantages et des inconvénients. Dans le chapitre qui suit, une étude détaillée de ces méthodes et une comparaison théorique entre elles, seront données.

1.5 Conclusion

Dans ce chapitre, nous avons présenté une brève introduction à la stratégie de rendez-vous, aux systèmes multi-agents et leur application dans le domaine de la robotique mobile pour mieux appréhender la suite du projet.

Chapitre 2

Différentes approches de la stratégie

de rendez-vous

2.1 Introduction

Dans ce chapitre, nous étudierons plus en détail le problème de rendez-vous, les différentes approches adoptées par Smith [1] ainsi que les méthodes associées.

Un schéma analytique du problème sera présenté pour chaque méthode, vu qu'on utilise l'approche de calcul numérique, par référence aux travaux de Smith.

Dans le but de concevoir une stratégie de rendez-vous, plusieurs méthodes suivant différentes approches ont été étudiées dans la thèse de Smith, et ce dans le but de trouver la méthode la plus efficace, la plus rapide et aussi la moins coûteuse. Dans la première partie de ce chapitre, nous expliquerons la première approche, qui est la poursuite cyclique et dans la deuxième, le rapetissement de courbe appliqué au SMA.

2.2 La poursuite cyclique

Il a été montré dans la littérature que le point de convergence d'un groupe d'agents et les mouvements des agents mobiles autonomes peuvent être commandés en employant des lois de poursuite cyclique (généralement utilisée dans la commande de véhicules).

Smith et autres ont mis en place un modèle mathématique décrivant cette stratégie comme suit : un groupe d'agents représentés par des points de masses, numérotés de 1 à n, la position de chaque agent peut être décrite dans un plan complexe par le point z = x + jy , i = 1, ..., n, avec j = J--1

z = x + jy

CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE DE RENDEZ-VOUS 16

La stratégie est telle que l'agent « i » chasse l'agent « i+1 ». La vitesse de l'agent « i » en direction de l'agent « i+1 » est donnée par le modèle suivant :

_zi _=zi+1-zj, i=1,...,n-1

(2.1)

_zri = z1 - zri.

Suivant ce schéma, les agents vont converger à leur centre stationnaire. Plusieurs stratégies peuvent être inspirées de ce modèle de base, c'est ce que nous verrons dans cette section. Mais avant, nous allons définir quelques concepts mathématiques utiles à la suite du chapitre.

2.2.1 Préalables mathématiques

Pour continuer, nous avons besoin de définir quelques concepts mathématiques utiles à la conception de notre système, tels que les matrices circulantes, et circulantes par blocs, la diagonalisation de matrices circulantes...

Matrices circulantes

Considérons un n-uplets (c1, C2, C3, ..., _cri) de nombres réels. La matrice circulante, est une matrice carrée (n x n) dont les lignes sont composées du n-uplet décalé à droite cycliquement modulo n. La forme générale d'une telle matrice est la suivante :

6 6 6 Cri C1 C2 ~ ~ ~ Cri_1 6 6 C = 6 Cri_1 Cri C1 ~ ~ ~ Cri_2				(2.2)
... 2 C1 C2 C3 ~ ~ ~ Cri	...	...	.. .. ..

C2 C3 C4 ~ ~ ~ C1

D'une façon plus explicite, nous écrirons :

C =: circ(c1, C2, C3, ..., cri)

Définition 2.1 En algèbre linéaire, une matrice carrée M d'ordre n (nEN*) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c'est-à-dire s 'il existe une matrice inversible F telle que F _¹MF soit une matrice diagonale.

CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE DE RENDEZ-VOUS 17

C =cnP ⁿ¹ + cn_1P n2 + ... + c2P + c1I (2.3)

avec:

010---0

001---0

P= =circ(0,1,0,...,0) (2.4)

... ... ... ... ...

100---0

Remarque 2.1 Ceci découle du fait que:

P2 =circ(0,0,1,0,..0,0), P³=circ(0,0,0,1,0,..,0), ...

Après certaines transformations sur la matrice C, nous obtenons la formule . 3. Définition 2.2 posons :

qc(s) = c_ns^n_1 + cn_1s^n~2 + ... + c2s + c1s^°

d'où:

C = qc(P)

Pour le calcul des valeurs propres de C, que nous noterons VP(C), nous devons d'abord calculer les valeurs propres de la matrice P. Davis [10] a montré que :

VP(C) = {q_c(.X) : 2 VP(P)}

Par définition de la matrice P dans [10] :

VP(P) = {1,e^2~jIⁿ,e^4~jIⁿ,...,e^2(n_1)~jIⁿ} (2.5)

Posons w = e2~iIn d'où:

VP(P) = {1,w,w²,...,w^n_1}

= VP(C) = fq_c(1)_; q_c(w)_; q_c(w²)_; :::; q_c(w^n~1)g

Après quelques calculs [1], nous obtenons la matrice diagonale:

CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE DE RENDEZ-VOUS 18

q_c(1) 0
·
·
· 0

A= 0 q_c(w)
·
·
· 0

...

...

. . . . . .

0
·
·
· 0 q_c(w^n-1)

C = FAF^* avec F la matrice inversible de passage de la forme :

1

F=

^,Vn

1 1
·
·
· 1

1 w
·
·
· wn-1

. .

. .

. .

... ...

1 wn-1
·
·
·w(n-1)(n-1)

De cette manière, nous aurons montré que la matrice circulante est diagonalisable.

Matrices circulantes par blocs

La matrice circulante par bloc est une matrice circulante où chaque réel dans la matrice 2.2 est remplacé par une matrice carrée Di (m x m), elle a la forme suivante :

2 D1 D2 D3
·
·
· D_n

6 6 ₆D_n D1 D2
·
·
· Dn-1

₆

D =6 6Dn-1 D_n D1
·
·
· Dn-2

...

...

...

. . . . . .

D2 D3 D4
·
·
· D1

C'est une matrice de dimension (nm x nm), et elle peu aussi être écrite en fonction de la matrice P(n x n) :

D= P ^n-1 0D_n+P^n-20D_n-1+
·
·
·+P0D2+I0D1

Définition 2.3 0 représente le produit de kronecker.

Le produit de kronecker entre deux matrices A(n x m) et B est définie comme suit :

a11B
·
·
· a1mB

A 0 B =

...

. . . . . .

an1B
·
·
· anmB

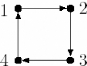
FIG. -1 - la structure d'une poursuite cyclique traditionnelle à 4 agents

Les valeurs propres de A ® B sont données par tous les produits possibles entre les valeurs propres de A et B.

2.2.2 Poursuite cyclique traditionnelle

C'est le cas le plus simple de la poursuite cyclique, où chaque agent poursuit l'agent qui le suit dans l'ordre de numérotation, tel qu'il est décrit dans le système 2.1. Ce système peut aussi s'écrire dans la forme vectorielle suivante :

z_ = A1z (2.6)

où A1 = circ(--1, 1,0, ..., 0). La matrice A1 = P -- I où P est donnée par 2.4. Smith a démontré le théorème suivant dans sa thèse [1] :

Théorème 2.1 Considérons la poursuite cyclique dans le schéma . 6, pour toute configuration initiale, le centre des agents z1(t), z2(t), ..., z,(t) est stationnaire et tous les zi(t), (i = 1,..., n) convergent à ce centre.

Le centre des agents est donc stationnaire, et est donné à chaque instant "t" par l'expression

1
n

z^~ =

_X,
i=1

suivante :

zi(t) (2.7)

Exemple 2.1 Prenons le cas de 4 agents, la poursuite cyclique est représentée par le schéma -1, et la matrice de transformation est :

--1 1 0 0

0 --1 1 0

A1=

0 0 --1 1

1 0 0 --1

2.2.3 Poursuite cyclique hiérarchique

Dans cette partie, le concept d'hiérarchie est introduit et appliqué à la poursuite cyclique. La hiérarchie veut dire une organisation des agents selon une hiérarchie de groupes en plusieurs couches. Le cas le plus simple est le schéma hiérarchique à deux couches, en suite nous étudierons un schéma plus général avec un nombre de couches quelconque.

Schéma hiérarchique à deux couches

Dans ce cas, les n agents de la poursuite cyclique traditionnelle sont répartis en n2 groupes de tailles identiques, chaque groupe contenant n1 agents (n1 x n2 = n). La stratégie est donc que, les agents d'un groupe sont en poursuite cyclique (traditionnelle), et leurs centres respectifs le sont aussi. Ceci veut dire que le centre de chaque groupe d'agents poursuit le centre du groupe suivant dans l'ordre de numérotation des groupes.

Chaque agent est caractérisé par sa position, dans un plan complexe, notée _zi,j où i (i = 1, :::, n2) représente l'indice du groupe, et j (j = 1, ..., n1) l'indice de l'agent dans le groupe "i". Le schéma décrivant cette stratégie, et ainsi les vitesses de déplacement des agents est le suivant :

	8	_z1,1 = z1,2 -- z1,1 + d1,1
	<>>>>>>	_z1,2 = z1,3 -- z1,2 + d1,2
groupe 1	>>>>>>:	}		(2.8)
		...
		_z1,n1 = z1,1 -- z1,n1 + d1,n1
...
	8	_zn2,1 = zn2,2 -- zn2,1 + dn2,1
groupe 2	<>>>>> >	_zn2,2 = zn2 ,3 -- zn2 ,2 + dn2,2	}
		...
	>>>>>>:
		_zn2,n1 = zn2,1 -- zn2,n1 + dn2,n1

Où les _di,j sont les déplacements des agents, la question est donc, : comment choisir ces déplacements pour réaliser la stratégie décrite par 2.8

L'équation de déplacement des centres, sachant qu'ils réalisent une poursuite cyclique, est :

:

zi = ^~zi+1 -- zi, i = 1, ..., n2 -- 1 (2.9)

:

^~zn2 = ^~z1 -- ^~zn2

CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE DE RENDEZ-VOUS 21

1

n1

^~zi =

_Xn 1
j=1

où le centre du groupe "i" est donné par:

zi_;j (j = 1, ..., n1) (2.10)

1

n1

:

^~zi =

_Xn 1
j=1

en dérivant ce système, nous obtenons la vitesse de déplacement du centre du groupe "i" :

di_;j (j=1,...,n1) (2.11)

car, d'après 2.8 :

_Xn 1 _zi,j = _Xn 1 di_;j Vi= 1,...,n2

j=1 j=1

d'après 2.11 et en remplaçant dans 2.9, nous obtenons :

Xn 1 j=1					: di;j = n1 ^~zi= n1(^~zi+1 - ^~zi) (2.12)
Pn2 = i=1	Pn1 j=1	di;j = n1	n2 P i=1	: ^~zi = 0

= le centre des n agents est stationnaire.

Plusieurs _di;j peuvent être choisis satisfaisant 2.12, l'un des choix : di_;j = zi+1,j - zi,j.

Ceci veut dire que l'agent "j" dans le groupe "i" poursuit l'agent "j" dans le groupe "i+1". Si on remplace les _di;j par leurs expressions dans 2.8, nous obtenons la dynamique de l'agent "j" du groupe "i" :

_zi_;j = zi,j+1 - zi_;j + zi+1,j - zi_;j (2.13)

nous remarquons que l'agent "j" du groupe "i" a un lien avec l'agent "j+1" du même groupe, et un lien avec l'agent "j" du groupe "i+ 1". D'où chaque agent aura besoin de deux liens de communication (capteurs). Avec cette stratégie, le système comporte 2n senseurs.

L'équation 2.13 s'écrit dans une forme vectorielle :

z_=Bz+Dz

où B est la matrice diagonale par blocs représentant la poursuite cyclique à l'intérieur d'un groupe.

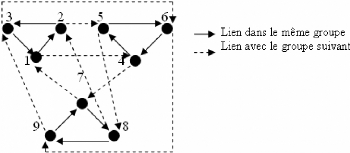
FIG. 2-2 - Structure d'un schéma hiérarchique à 2 couches (9 agents, 3 groupes)

avec A1 = (P - I)(n 1Xn1) telle qu'elle est définie dans la poursuite cyclique traditionnelle. La matrice D représente les _di;j et est donc de la forme :

D = circ(-1,1,0,...,0)(n2Xn2)®In1

= (P - I)(n2xn2) ® In1 = circ(-I, I,0,... , 0)

où In1 = S représente les connexions de chaque agent dans un groupe aux agents du groupe suivant.

Un "1" dans la fg^~emeposition de la matrice S (f,g = 1, ...,n1) indique que le ^f~eme agent dans un groupe détecte le ^g~eme agent du groupe suivant (modulo n2).

posons A2 = B+D = circ(A1 -I, I,0, ..., 0), où A2 est une matrice circulante à blocs de dimension (n x n) où chaque bloc est de dimension (n1 x n1).

le système devient alors :

z_ =A2z

Exemple 2.2 Considérons un groupe de 9(n) agents, et un schéma hiérarchique à deux couches, avec 3(n2) groupes de 3(n1) agents (voir figure 2-2). La matrice de transformation est donc :

2 -1 1 0 6 6 A2 = circ(A1 - I,I,0,...,0) avec A1 = 6 0 -1 1 4 1 0 -1 A2 = circ(-2, 1,0, 1,0,0,0,0,0).

= circ(-1, 1,0). et I =

100 010 001

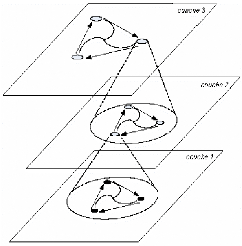
FIG. 2-3 - Trois couches d'hiérarchie dans une poursuite cyclique

Schéma général

Dans un schéma plus général, nous avons L couches d'hiérarchie. La première couche contient n1 agents, la deuxième contient n2 sous-groupes de n1 agents, la troisième n3 groupes de n2 sous- groupes de n1 agents, ... (voir Figure 2-3)au total, nous avons _r'L n_m = NL.

m=1

Le système est le suivant :

z_=ALz (2.14)

où z est un vecteur colonne de taille NL (le nombre d'agents global), et AL est une matrice de dimension (NL x NL). Pour L = 1, la matrice A1 = (P - I)n1~n1:

A chaque fois que nous ajoutons une couche, nous devons nous assurer que le comportement de la couche inférieure reste stable. Ceci veut dire que les agents / les groupes de la couche inférieure restent en poursuite cyclique. Des senseurs sont ajoutés entre les centres des groupes d'une même hiérarchie, pour qu'ils réalisent une poursuite cyclique au niveau supérieur. Comme pour le schéma hiérarchique :

- Les A1 au long de la diagonale représentent la poursuite cyclique dans chaque groupe.

- Les "-I" au long de la diagonale, associés aux "I" au long des blocs qui suivent, représentent les connexions entre les groupes pour créer la nouvelle couche d'hiérarchie.

Chaque agent dans un groupe prend la position de l'agent dans le groupe suivant moins sa propre

position, pour créer la nouvelle hiérarchie. Une hiérarchie à L couches est décrite par le système 2.14 où, la matrice AL est obtenue de façon récursive à partir de A1, de la façon suivante:

A1 = circ(-1,1,0,...,0) (2.15)

A_m = circ(Am_1 - I,I,0, ..., 0) m = 2, ..., L

où A_m est une matrice composée de n_m blocs de dimension Nm_1 ^X Nm_1.

Le nombre de liens de communication:

Nous remarquons que, pour mettre en place chaque nouvelle couche, tout agent doit avoir un lien avec un agent d'un autre groupe, ceci est décrit par la deuxième diagonale "I" dans 2.15. D'où chaque agent aura L liens de communication avec les autres agents. Ainsi, le système compte un total de LNL liens.

La question qui se pose naturellement est comment choisir la distribution d'agents qui donne le meilleur taux de convergence (que nous calculerons dans la dernière partie de cette section)? Smith [1] a introduit et démontré le théorème suivant :

Théorème 2.2 Dans le cas où /NL est un entier, la distribution uniforme des n_m :

pn1 = n2 = ~ ~ ~ = nL = NL (2.16)

est une distribution optimale. De plus elle est la seule à l'être. Sachant que la distribution optimale, qui satisfait _r'L n_m = NL, est celle qui donne le taux de convergence le plus important.

m=1

Remarque 2.2 Cette solution donne une augmentation dans le taux de convergence équivalente à

RL = _N2(n_1)' L

_L que nous verrons ensuite comment calculer.

Remarque 2.3 Quand pNL n'est pas un entier, il peut exister plusieurs distributions optimales.
Par exemple, pour NL = 12, L = 2, deux solutions optimales : {n1, n2} = {3, 4} et {n1, n2} = {4, 3}.

2.2.4 Poursuite cyclique à L liens

En comparant, dans la partie qui va suivre, les deux techniques étudiées précédemment, la pour-
suite cyclique hiérarchique donne un taux de convergence plus élevé que le schéma traditionnel.
Cependant, elle demande plus de liens de communication entre les agents, chaque agent perçoit plus
d'un agent contrairement au traditionnel où chaque agent ne capte que l'agent qui le suit dans l'ordre.
Pour cette raison, un schéma intermédiaire a été introduit où le nombre de connexions entre
agents est inférieur au schéma traditionnel, ou plus ou moins contrôlé, et où chaque agent chasse le

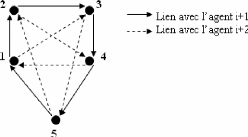
FIG. 2-4 - Structure d'une poursuite cyclique de 5 agents à 2 liens.

centre d'un groupe d'agents.

Dans une poursuite cyclique à L liens, chaque agent possède un lien de communication avec "L" agents. S'il y a NL agents, alors il y aura un total de LNL connexions dans le système. La stratégie que nous adopterons est la suivante :

Dans un système de NL agents, l'agent "i" poursuit le centre des agents de "i+1" jusqu'à "i+L" (modulo NL). Formellement ceci s'écrit :

1
L

_zi=

_XL
m=1

zi+m(modNL) ~ zi i=1, . . . ,NL.

ou sous une forme vectorielle : _zi = Az avec _ANLXNL une matrice circulante de la forme :

,0,...0) (2.17)

| _{z }

L uns

circ(--L,1,... 1

1

A= L

Exemple 2.3 Prenons le cas de NL = 5 agents, avec L = 2 (voirFigure e-4). la matrice de transformation A est la suivante :

A = 1 ₂circ(-2, 1,1,0,0) = circ(-1,¹ 2, ¹ 2,0,0).

2.2.5 Comparaison et taux de convergence

Dans cette partie, nous comparerons entre les trois différentes méthodes de la poursuite cyclique. Cette comparaison servira à faire une sélection entre les méthodes selon différents facteurs, elle sera ensuite appuyée par les résultats de notre simulation au dernier chapitre.

En plus du temps de convergence et de la vitesse moyenne des agents calculés à la fin de la simulation, un rapport est calculé pour exprimer l'augmentattion dans le taux de convergence entre

chaque couple de méthodes : Schéma traditionnel / l'hiérarchique, hiérarchique / Poursuite cyclique à L liens et ce dernier / schéma traditionnel.

Définition 2.4 Le taux de convergence des agents à leur centre est déterminée à partir de la valeur propre non nulle de A2 avec la partie réelle absolue la plus petite, nous appellerons cette dernière "valeur 'y".

Définition 2.5 L'augmentation dans le taux de convergence (R) calculé représente la rapidité de convergence du groupe d'agents au centre, avec une méthode comparé à l'autre méthode, c'est un rapport entre les parties réelles des valeurs 'y des deux différentes méthodes :

Ï(valeur 'y(m^~ethode 1))

R = Ï(valeur 'y(m^~ethode 2)) Ï: La partie réelle du nombre complexe.

Poursuite cyclique traditionnelle / hiérarchique

Soit : NL le nombre d'agents total.

Le taux de convergence correspondant à cette comparaison est:

Ï(valeur 'yhier)(2.18) Ï(valeur 'ytrad)

RL = traditionnel

hierarchique

Pour trouver la valeur 'y, nous devons d'abord calculer les valeurs propres de la matrice de transformation correspondant à la méthode utilisé AL (A1).

D'après 2.15, la matrice A_m est une matrice circulante à blocs, ses valeurs propres sont donc :

VP(A_m) = nm_[ VP(Am_1 + ^{(e2~j(r_1)Inm} - 1)I)

r=1

donc, les VP(A_m) sont les n_m ensembles de _{VP(Am_1)} décalées à gauche par a_m(r) = e2~i(r_1)Inm1. Nous remarquons que :

-2< Ï(a_m(r))<0 Vr=1,...,n_m.

car : Ï(o_m(r)) = cos(2r(r - 1)/n_m) - 1. et -1 < cos(2r(r - 1)/n_m) < +1.

Pour trouver la valeur 'y, nous devons d'abord déterminer toutes les valeurs 'y possibles de VP(A_m). Ces valeurs 'y appartiennent aux ensembles des VP avec le décalage à gauche le plus petit.

- Le premier ensemble des VP(A_m), elles sont simplement les _{VP(Am_1)} décalées par a_m(1) = 0, donc les valeurs 'y possibles de cet ensemble sont les valeurs 'y des VP(Am_1).

- L'ensemble des VP avec le décalage suivant le plus petit est donné par Am_1 + a_m(2)I (ou également a_m(n_m))[1]. Pour cet ensemble, la VP nulle de _{Am_1(la} VP la plus à droite) est décalée à gauche de a_m(2). Elle est donc la valeur 'y de cet ensemble, et est donnée par:

'y_m := e2~jInm - 1

De cette façon, on constitue l'ensemble des valeurs 'y possibles. Ensuite, la 'y-value des VP(A_m) doit être, ou la valeur 'y des _{VP(Am_1),} ou bien 'y_m. Ceci est un schéma récursif, pour chaque couche ajoutée, une autre VP est ajoutée à l'ensemble des 'y - values possibles. Plus concrètement :

Pour la première couche, la valeur 'y des VP(A1) est : 'y1 := e2~u/n1 - 1.

La deuxième couche, la valeur 'ye des VP(A2) est la valeur 'y des VP(A1) qui n'est autre que 'y1 ou bien : 'y2 := e2~3/n2 - 1.

De même pour la troisième couche, la valeur 'y des VP(A3) est 'y1, 'y2 ou : 'y3 := e2~3In3 - 1.

...

Pour les VP(A_m) la valeur 'y du schéma hiérarchique à L couches est donnée par:

'y := e2~j' - 1 w = max m

{nm}, m=1,...,L.

Pour la poursuite cyclique traditionnelle, il n'existe qu'une seule couche donc, la valeur 'y est donnée par : 'y := e2~j'NL - 1.

Ainsi, à partir de 2.18 l'augmentation du taux de convergence utilisant le schéma hiérarchique en comparaison avec la poursuite cyclique traditionnelle est :

Hi^~erarchique R = Traditionnel

<(e^2~iI - 1) <(e^2~iI^NL - 1)

cos(2r/w) - 1 cos(2r/NL) - 1

Pour simplifier cette expression, nous remplaçons le cos par son développement limité de l'ordre

1 avec :

cos(x) = _Pn

i=0 (_1)ⁱ

_(2i)! x2n + o(x²ⁿ) à l'ordre 2n avec o(x²ⁿ) -! 0 cos(x) à l'ordre 1 : cos(x) = 1 - ¹ ₂x². d'où :

1_1 2 (2ir/$)2_1 R 1_ 2 1 (21r/NL)2_1

~ 2=$ ) 2 ~NL 2 ~ NL 2 = = = 21r/NL $ maxm{nm}

Remarque 2.4 Dans le schéma hiérarchique à deux couches, le taux de convergence est directement:

max{n1, n2}

NL = min{n1,n2}²

(R2 =

2

Cas particulier: Lorsque n1 = n2 = /N2 les N2 agents convergent approximativement N2 fois

plus rapidement utilisant le schéma hiérarchique qu'utilisant la P.C traditionnelle.

.

Remarque 2.5 Pour la distribution optimale des n_m, trouvée précédemment concernant le schéma hiérarchique général. Et d'après 2.16 Le taux de convergence est :

~ (

( _NL J 2 ~ 2 ~ J 2 ~ 2

L1

NL L

R L = NL ~ N_1IL = N2(L_1)=L

L pNL = = = N

_N1/L L L L

L

Dans tous les cas, RL ~ 1 et donc, la convergence au centre utilisant une hiérarchie se fait plus rapidement que le schéma traditionnel.

Cependant, le schéma hiérarchique nécessite plus de liens de communications que le traditionnel, d'où plus de senseurs => il est donc plus coûteux.

Poursuite cyclique hiérarchique / à liens

De la même manière, nous retrouvons la valeur 'y de la poursuite cyclique à L liens, pour la comparer à celle du schéma hiérarchique, et calculer le taux de convergence.

D'après la formule 2.17 et utilisant la forme polynomiale de la matrice A qui est : A = q_c(P) avec : q_c(s) = 1 _Ls^L + ¹ _Ls^L_1 + ... + ¹ _Ls - s⁰,

VP(A) = ~q_c(1), q_c(w), q_c(w²), ..., q_c(w^NL_1)~

avec : w = e2~j=NL

La matrice A est circulante, elle possède donc une seule VP nulle q_c(1) et toutes les autres se situent dans la partie gauche du plan. S.L. Smith [1] a montré qu'il faut que NL » L pour que la valeur 'y des VP(A) soit donnée par q_c(w) = 'y.

XL 1 'y = qc(w) = L(w + w^2 + ~ ~ ~ + w^L) - 1 = 1 L m=1

e2~jm=NL - 1

et la partie réelle de est :

XL 1 <('y) = L m=1

(cos(2mr/NL)) - 1

CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE DE RENDEZ-VOUS 29

Ainsi, le taux de convergence est :

Hi^~erarchique R = L-lien

cos(2r/w) - 1

(cos(2mr/NL)) - 1

=

avec w = max{n1, n2, ..., nL}

1
L

_PL
m=1

Toujours en utilisant le développement limité du cosinus, simplifions cette expression :

1_1 ₂ (2ir/$)2_1

R = PL

m=1

(27r $ )2

=

( _27r )2 1 PL

_m2

NL L m=1

(NL )2

L ~ :

$

(1_1 ₂ ( 27rm

NL )2)_1

_PL
m=1

1
L

_m2

1
L

_PL
m=1

De même, nous avons: R ~ 1 et donc, le schéma hiérarchique à L couches converge plus rapidement que celui à L liens, même s'ils demandent tous les deux le même nombre de capteurs.

Poursuite cyclique à L liens / Traditionnelle

Dans les comparaisons précédentes, nous avons calculé les valeurs 'y correspondant aux deux méthodes respectives (traditionnelle, L-liens). D'où l'augmentation dans le taux de convergence de la P.C à liens comparée à la traditionnelle est la suivante :

L - liens

R = Traditionnelle

(cos(2mr/NL)) - 1

=

cos(2r/NL) - 1

Après simplification du cos par son développement limité de l'ordre 1 :

(1_1 ₂ ( 27rm

NL )2)_1

1_ 1 2 (21r/NL)2_1

_PL

_Pm=1 2 ( 27r

1 NL )2 =m=

m2 ~ 1 = Les agents avec le schéma à L liens

R=

1

1_1 ₂ ( NL 27r )2

m²_1 L

1
L

_PL
m=1

convergent plus rapidement qu'avec le traditionnel, mais demandent plus de liens de communications et donc plus de senseurs.

2.3 Le rapetissement de polygone

Dans cette section, nous appliquerons la théorie du rapetissement de courbe aux SMA. Si on considère que les agents représentent les sommets d'un polygone, en utilisant les résultats du rapetissement de courbe euclidien, nous prouvons que ce polygone va se rétrécir jusqu'à devenir un point qui n'est autre que le centre des agents, et par ce fait réaliser la stratégie de rendez-vous.

Nous commencerons par un aperçu mathématique sur la géométrie euclidienne, le rapetissement de courbe, les différentes propriétés des polygones, ensuite nous étudierons deux méthodes mise en oeuvre par S. L. Smith [1] qui appliquent le rapetissement de polygone au problème de rendez-vous, dont Menger-Melnikov, et un autre schéma linéaire.

Considérons toujours le système représenté ci-dessous, où les z sont les positions des agents et

_zi leur vitesses respectives :

_p

zi = xi + jyi i = 1, . . . , n j = -1

_zi = ui

où ui est calculé en fonction de la méthode utilisée.

2.3.1 Préalables mathématiques

Dans ce qui suit, et pour pouvoir poursuivre, un aperçu sur la géométrie euclidienne, la dynamique du rapetissement de courbe qui en dérive, ainsi que quelques propriétés des polygones.

Géométrie euclidienne

Définition 2.6 Une transformation euclidienne de R² est une fonction L : R² . R², L(x) = Ux+a. Où U est une matrice orthogonale (2 x 2), a 2 R.

U est une matrice orthogonale == U^~1 = UT

L'ensemble des transformations euclidiennes est l'ensemble de toutes les rotations, translations, réflexions d'une figure dans R². Autrement dit, la géométrie euclidienne est l'étude des propriétés des figures qui restent inchangeables par des transformations euclidiennes. Ces propriétés euclidiennes comprennent la distance, la courbure et la colinéarité des points.

Rapetissement de courbe euclidien

Soit une famille de courbes lisses et fermées, x(p, t) : [0, 1] x [0, r] - R², situées dans un plan complexe où p désigne les points le long de chaque courbe et t la famille de courbe. La courbe initiale x(p, 0) évolue en fonction du temps à x(p, r). Nous allons considérer dans un premier temps seulement la première courbe noté x(p) = (x1(p), x2(p)).. Le vecteur tangent à la courbe est donné par^dx

dp = _x, son vecteur unité est T(p) = x_

k _xk = ( _x1(p)_; _x2(p))

k _xk .

et le vecteur unité de la normal qui est perpendiculaire à la tangente (N(p) T(p) = 0) est : N(p) = (~ _x2(p)_j _x1(p))

k _xk .

Un nouveau paramètre de la courbe sera introduit pour les prochains calculs "s" qui représente la longueur d'un arc, et ce afin de décrire la distance autour de la courbe au lieu de p. Avec ds = k _xk dp.

_{F 3 F 3}

LT T L x' ₁ x' ₂

Soit la matrice de rotation A(s) = ] = ] où ⁰ décrit la différentielle par rapport

NT -x ' 2 x' ₁

à "s". Pour calculer la dynamique du système, nous allons d'abord calculer la dynamique des deux

vecteurs N et T pour obtenir l'équation de Frenet [12]. C'est à dire A'.

CHAPITRE 2. DIFFÉRENTES APPROCHES DE LA STRATÉGIE DE RENDEZ-VOUS 31

A^' = A^GA^~1A = C(s)A Trouvons C(s)?

A-1 = A^T = X₀ --X₂

₀01

(matrice orthogonale)

[ ⁰

X2X1

₂

A^' = 4

» »

X1 X2

--X »2 X » 1

_3
5

_{2 3 2 3 2 3}

» » 0 0 0 » 0 ^»C(s) = 1 = X1 X2 X1 --X2 = X1X1 + X2X2 X;X^'2^' -- X;i2 _{4 5}

0 0 » 0 0

--X2 X₁ X₂ X1 --X1X2 -- X1X2 X1X1 + X2X2

_{2 3}

0

j 0 X1

posons : k(s) = X1X2 -- X1X2 = det ₅= det(X^, ,X^, ). Où k(s) est la courbure de la courbe

X2 X2

X(s) et le rayon de courbure est : ¹

1i(s)1^-

Nous avons aussi :

(AAT)/ = A/AT + A(AT)/ = A/A-1 + (A-1)T(A/)T = A/A-1 + (A/A-1)T

Avec : --(AAT )/ = 0, puisque : AA^T = I. --A^/A^-1 = C(s)

et donc : C(s) = --C(s).

[ 0 "

--X1X1 -- X2X2 --X1X2 + X1X2

» 0 0 » 0 » 0 »

X1X2

+

X1X2--X1X1

--

X2X2

--C(s) =

C(s) = --C(s) ) 0 » 0 » X1X1 + X2X2 = 0 D'où :

8 < :

0 » 0 » 0 » 0 » X1X1 + X2X2 = --X1X1 -- X2X2 0 » » 0 0 » » 0 X1X2 -- X1X2 = --X1X2 + X1X2

}

0 » 0 j ), i i , X1X1 + X2X2 = --(X1X1 + X2X2) )

C(s) =

[ 0 k(s)1

--k(s) 0 (2.19)

Retrouvons la dynamique du système :

dT

A(s) =[1 A^/ (s) = [dd _{ds N}^s1 A^-1(s) = h_T-1 _N-1i

N^T

d'après 2.19 :

2 A^GA^-1 = 4 dT

dT ds dN ds

3hT-1 N-1i --k(s =[ 0 k(s)1 ) 0

)

8 < :

dTds N^-1 = k(s) dNds T^-1 = --k(s)

}

{

^dTdsN^-1N = k(s)N ^dd^Ns T^-1T = --k(s)T

}

)

8 < :

dTds = k(s)N ^dd^Ns = --k(s)T

}

)L'équa-

2 )4

ds T^-1 ds T-1 N-1 T dN T-1 dN N-1 ds ' ds

1= [ 0 k(s)1 --k(s) 0

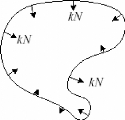
FIG. 2-5 - La dynamique du rapetissement de courbe

Dans la dynamique du rapetissement de courbe Euclidien, la courbe x(p, t) est déformée le long de son vecteur normal N(p, t) avec un taux proportionnel à sa courbure k(p, t). Et donc:

Dx

3p (p,t) = k(p,t)N(p,t) (2.20)

La formule 2.20 décrit la dynamique du rapetissement de courbe Euclidien x(p, t) tel qu'il est montré dans la figure 2-5.

Rapetissement de polygone

Nous allons appliquer les résultats de Smith et autres concernant le rapetissement de courbe aux systèmes multi-agents. Considérons un groupe d'agents mobiles autonomes situés dans un plan et formant les sommets d'un polygone à "n" cotés (voir la figure 2-6). En créant un schéma de rapetissement de polygone semblable à celui du rapetissement de courbe, les sommets (les agents) convergeront à un point elliptique. Ainsi, la forme du polygone se rétrécissant à un point aura les mêmes propriétés que la théorie du rapetissement de courbe. Avant, nous donnerons une définition formelle d'un n - gons ainsi que quelques propriétés intéressantes.

Définition 2.7 Un n - gons est un circuit de "n" segments de ligne : z1z2, z2z3,. . . , z_nz1,joignant chaque paire de points consécutifs : z1, z2, . . . z_n. Les segments sont appelés cotés, et les points sommets.

Définition 2.8 Un polygone simple est un n - gons avec les cotés non intersectés. Notons I3i les angles internes (dans le sens contraire des aiguilles d'une montre) entre les côtés consécutifs zizi+1 et _{zi_1zi} d'un polygone. i = 1,.. . , n(modulo n). Ces angles satisfont :

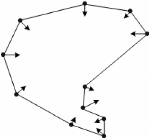
FIG. 2-6 - Rapetissement de polygone

Définition 2.9 Un n - gons convexe est n - gons simple dont les angles internes satisfont : 0 ~ /3i ~ 7r,Vi=1,...,n.

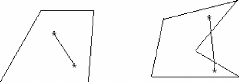
Polygone convexe Polygone concave

Une ligne tracée entre n'importe quels deux points distincts du n-gons convexe appartient toujours à celui-ci.

2.3.2 Rapetissement par la courbure de Menger-Melnikov

Considérons le cas où nous connaissons seulement quelques points discrets x(pj), i = 1,... , n d'une courbe lisse x(p) (voir la figure 2-6). En connectant ces points, nous obtenons un n - gons. Quand n - oc le n - gons n'est rien d'autre que la courbe même.

Il existe un unique cercle circonscrit qui passe par n'importe quels trois points, non colinéaires, x(pj_1), ^x(pj), _x(pj+1) ^où pj_1 < pi _<pj+1 sur la courbe x(p) comme sur la figure 2-7.

R(pi) est le rayon de ce cercle, et Ci(pi) le centre circonscrit. La quantité ¹

R(pi) est appelé la

courbure de Menger-Melnikov et a la propriété suivante :

lim pi-1 ,pi+1!pi

1 R(pi)

= Ik(pi)I

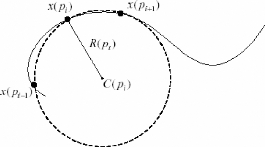
FIG. 2-7 - Le cercle circonscrit de 3 points de la courbe

Quand les deux points _{x(pi_1)} ^et _{x(pi_1)} sont proches de x(pi) :

C(pi) -- x(pi) R(pi) --*		8 <>>> >>>:	N(pi) si k(pi) > 0 ou --N(pi) si k(pi) <0	9 >>>= ;>> >
et donc : lim pi1 ,pi+1!pi	C(pi)_x(pi) R(pi)2 = k(pi)N(pi).

Utilisant cette méthode, un schéma discret analogue au rapetissement de courbe euclidien peut être mis en oeuvre. Considérons "n" agents z1, z2,.. . z, situés dans un plan complexe, et formant un n -- gons. pour chaque 3 sommets consécutifs : zi_1, zi,zi+1, la fonction suivante est définie:

(zi_1^--zi_-- zi+1 -- zi ~ 1

ci = c(zi_1, ^zi, zi+1) = (2.21)

zi_1 -- zi zi+1 -- zi zi_1 -- zi+1

où zi est le conjugué complexe. zi = xi + jyi = xi -- jyi.

Dans [1], il a été démontré que lcil est la courbure de Menger-Melnikov pour les 3 points zi_ 1, zi, _zi+1. Le centre circonscrit est donné par: zi+Ci

jCij2 . Le vecteur normal pour zi est approximé à

jCij. Et donc, la dynamique de la courbure de Menger-Melnikov décrit précédemment peut être écrit

Ci

comme suit :

_zi = c(zi_1,zi,zi+1)

Le nombre de liens de communication nécessaires pour réaliser ce schéma est de 2n, puisque chaque agent zi doit percevoir les deux agents _{zi_1} ^et zi+1:

L'évolution du polygone décrite par ce système a été étudié dans [11]. Mais vu la complexité de ce système et du calcul de ci, les résultats sont limitées. Il a été montré que :

- Un n - gons simple s'écroule en un point dans un temps fini, et pour n = 4, la plupart des quadrilatérales tendent à des polygones réguliers en se rétrécissant.

- Quand n est petit, pour un n - gons convexe, il peut exister un _zi qui ne se dirige pas vers l'intérieur.

- Quand le polygone s'écroule, la vitesse des sommets _zi devient infiniment grande, car le dénominateur dans ci devient très petit quand les points se rapprochent. Ceci n'est pas compatible avec les SMA, où la vitesse doit rester raisonnable.

Vu que les résultats obtenus avec cette méthode n'étaient pas très satisfaisants (ce qui va être confirmé avec les résultats de notre simulation au dernier chapitre), Smith a introduit un nouveau schéma linéaire pour le rapetissement de polygone.

2.3.3 Le schéma linéaire

L'idée est simple, nous considérons la même configuration d'agents précédente, la stratégie consiste à ce que chaque agent "j" chasse le centre de ses deux agents voisins (j - 1) et (j + 1). La vitesse de l'agent j est la distance qui sépare ce dernier du centre de ses 2 voisins :

_zi=	1 1 2(zi+1 - zi) + 2(zi_1 - zi) (2.22)

Avec: _zi = 1 2(zi_1 + zi+1) - zi.

Le nombre de liens de communication nécessaire pour ce schéma est aussi égale à 2n, pour les même raison que le cas précédent.

2.3.4 Remarques

- Smith [1] a montré qu'un groupe d'agents, disposés et formant une étoile autour de leur centre de gravité, restent dans cette forme pour le reste du temps jusqu'à arriver au centre.

- Il a aussi démontré qu'un n -gons convexe évoluant selon la formule 2.22 reste toujours convexe.

2.4 Conclusion

Dans ce chapitre nous avons étudié théoriquement les différentes approches utilisées pour effectuer une stratégie de rendez-vous de SMA, leurs caractéristiques ainsi que les limitations rencontrées lors de la conception. Un schéma hiérarchique a été introduit pour la poursuite cyclique. Nous avons aussi étudié la théorie mathématique du rapetissement de courbe appliquée aux SMA, des résultats

ont été explicitement déduits. Ils seront vérifiés dans le chapitre suivant où nous mettrons en oeuvre une simulation de ces différentes approches et méthodes relatives.

Chapitre 3

Mise en oeuvre de la simulation

3.1 Introduction

La simulation consiste à effectuer des expériences sur un modèle d'un système réel, dans notre cas, il s'agit d'une stratégie de collectivité de robots autonomes dans un environnement spécifique. Pour ce faire, nous décomposons cette activité en quatre étapes :

Analyse du système réel, et des informations que l'on désire obtenir sur son comportement.

- Représentation d'un modèle, dans lequel nous ne retenons que les caractéristiques qui semblent pertinentes par rapport aux résultats recherchés, sous forme d'un programme de simulation. L'expérimentation, dans laquelle nous faisons évoluer le modèle, c'est à dire interpréter le

programme de simulation à l'aide d'un schéma d'exécution adapté qui est le simulateur.

- Analyse des résultats produits, et en déduire des informations sur le comportement du système réel.

La première étape a été traitée dans le chapitre précédent. Dans celui-ci, il s'agit de prendre en charge les deux étapes qui suivent en développant une interface graphique sous forme d'une applet Java, pour simuler les différentes approches de la stratégie de rendez-vous et en déceler quelques caractéristiques. Dans le dernier chapitre, nous réaliserons la dernière étape.

Avant de procéder à la conception de l'interface de simulation, et compte tenu de la complexité des méthodes présentées au chapitre précédent, nous avons jugé nécessaire de passer par une étape intermédiaire, qui consiste à vérifier et à étudier la faisabilité des algorithmes. Ceci a été fait en utilisant Matlab, qui est un langage de calcul mathématique, car notre système implémente des algorithmes employant plusieurs d'outils mathématiques.

3.2 Vérification et implémentation des algorithmes sous Matlab

Avant de réaliser notre simulation sous Java, nous avons pensé à mettre en oeuvre des algorithmes implémentant les différentes stratégies et méthodes présentées au chapitre précédent. Cette implémentation permettra de vérifier la réalisabilité des algorithmes, de tracer les trajectoires des robots mobiles réalisant la stratégie de Rendez-vous, et de comparer entre les différentes approches. Cette étape fut très simple et très rapide, car Matlab offre une boite à outils mathématiques très riche contenant toutes les fonctions nécessaires à notre étude.

3.2.1 Résolution de la dynamique du système

Dans les deux approches adoptées pour réaliser la stratégie de Rendez-vous (Poursuite cyclique, Rapetissement de polygone), il s'agit de résoudre des systèmes dynamiques décrivant l'évolution d'agents mobiles autonomes dans un environnement spécifique. Ces systèmes sont régis par des équations différentielles d'ordre 1 qui sont sous la forme suivante :

x_ = f(t,x)

Pour résoudre ce type d'équation, nous utilisons la méthode de Runge Kutta d'ordre 4 [10] afin de calculer les positions des agents aux instants "t".

Définition 3.1 Les méthodes de Runge-Kutta sont des méthodes d'analyse numérique d'approximation de solutions d'équations différentielles. Elles portent le nom des mathématiciens Carl Runge et Martin Wilhelm Kutta. Ces méthodes reposent sur le principe de l'itération, c'est-à-dire qu'une première estimation de la solution est utilisée pour calculer une seconde estimation, plus précise, et ainsi de suite.

Algorithme 3.1 Algorithme de Runge Kutta d'ordre 4 Considérons le problème suivant :

x_ = f(t,x) x(t0) = x0 connu

La méthode de RK4 est donnée par l'équation:

xi+1 = xi +

h 6 (w1 +2w2 +2w3+w4)

w1 = f(t ,x )

w2 = f(t +h 2 ;x +h 2 k1)

w3 = f(t +h 2 ;x +h 2 k2)

w4 = f(t +h,x +hk3)

L'idée est que la valeur suivante x ₊₁ est approchée par la somme de la valeur actuelle x et du produit de la taille de l'intervalle h par la pente estimée. La pente est obtenue par une moyenne pondérée de pentes :

w1 est la pente au début de l'intervalle.

w2 est la pente au milieu de l'intervalle, en utilisant la pente w1 pour calculer la valeur de x au point t + h 2 par le biais de la méthode d'Euler.

w3 est de nouveau la pente au milieu de l'intervalle, mais obtenue cette fois en utilisant la pente w2 pour calculer x.

w4 est la pente à la fin de l'intervalle, avec la valeur de x calculée en utilisant w3.

Dans la moyenne des quatre pentes, un poids plus grand est donné aux pentes au point milieu.

pente =	w1 + 2w2 + 2w3 + w4
	6

L'ordre 4 signifie que l'erreur commise à chaque étape est de l'ordre de h⁵, alors que l'erreur totale accumulée est de l'ordre de h⁴.

3.2.2 Implémentation des algorithmes et tracé des trajectoires sous Matlab

Nous avons implémenté avec Matlab [13] les fonctions des différentes méthodes correspondant aux deux approches dont la poursuite cyclique et le rapetissement de courbe. Dans chacune d'elles, nous avons tracé des graphes affichant les trajectoires, effectuées par un groupe d'agents, pour vérifier leur convergence au point centre de gravité.

Poursuite cyclique

Pour effectuer cette stratégie, les agents évoluent selon le système ci-dessous avec la matrice A qui change suivant la méthode.

z_ =Az (3.1)

Remarque 3.1 Il existe une deuxième méthode pour la résolution du système 3.1, qui consiste à trouver itérativement les positions z telles que :

z = expm(At ).z0

Où expm(A) est la matrice exponentielle de A, et est calculée en utilisant la formule suivante :

expm(A) = V diag(exp(diag(D))) V ^~1

Avec D : un vecteur constitué de l'ensemble des valeurs propres, et V: la matrice des vecteurs propres correspondant.

Ceci revient à calculer les valeurs et les vecteurs propres d'une matrice de dimension n, et donc de résoudre une équation et un système d'équation de l'ordre n. Ce dernier pouvant être très grand, il devient très difficile de résoudre le système. En utilisant matlab, ceci fut simple à implémenter car la fonction expm est prédéfinie. Mais pour programmer la classe Java qui le résout, l'exécution de la fonction aura une très forte complexité dans l'utilisation des ressources (temps et espace mémoire). C'est pour cela que nous avons employé une méthode plus simple qui est celle de Runge Kutta d'ordre 4.

Poursuite cyclique traditionnelle Dans cette méthode, la matrice A de la formule 3.1 est une matrice circulante de la forme : A1 = circ(-1 , 1,0,.. . , 0), et l'algorithme est le suivant :

Algorithme 3.2

Début

% n est le nombre d'agents

% z est un tableau contenant les positions des agents % zn est le centre des agents

A1 = zero (n); % une matrice nulle de dimension n

Pour i = 0 à n - 1 % Construire la matrice circulante
j = (i+1) mod n;

A1(i,i) = -1;

A1(i,j) = 1;

fin pour

zn = mean(z) % la moyenne du tableau z

h = 0.1;

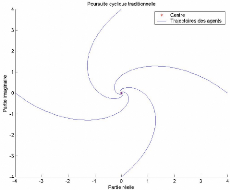
FIG. 3-1 - 4 agents dans une poursuite cyclique traditionnelle

Tant que (z =6 zn) % les agents ne sont pas au centre

wi = Al * z;

w2=A1 *(z+ (h/6) *wl); w3=Ai *(z+ (h/6) *w2); w4=Al *(z+h*w3);

z = z +((h/6) * (w1+2*w2+2*w3+w4));

fin tant que

fin.

Implémentant plus formellement cet algorithme sous matlab, et traçant un plot des positions "z", nous obtenons la courbe dans la figure 3-1 pour n = 4:

Poursuite cyclique hiérarchique Dans ce schéma, la matrice AL (L étant le nombre de couches) est circulante à blocs et est obtenue d'une manière récursive à partir de la formule 2.15.

L'algorithme de la poursuite cyclique hiérarchique est le même que celui de la traditionnelle avec une différence dans le calcul de la matrice A.

Algorithme 3.3 Début ...

% L est le nombre de couches.

% ni est le nombre d'agents de la première couche.

nm = L pn;

Am = circulante(L,n,n1,nm); zn = mean(z);

...

fin.

Et voici un pseudo code de la fonction circulante(L,n,n1,nm) :

Code 3.1 Fonction circulante(m,n,n1,nm)

début

si (m = 1) % la matrice A1

A = zero(n1); %la matrice nulle

pour i=0 à n1-1

j = (i+1) mod n;

A1(i,i) = -1;

A1(i,j) = 1;

fin pour

sinon

size = nm^m~1 ;

Id = eye(size); % La matrice identité de dimension size mat=circulante(m-1,n,n1,nm) - Id % La récursivité pour calculer Am-1
size = nm^m;

A =zeros(size2, size2);

pour cpt=0 à ((size2/size)-1)

pour i=0 à size-1

pour j=0 à size-1

k = i+size*cpt;

l =j+size*cpt;

r = (l + size) mod size2 ;

A(k,l)=mat(i,j); % Am-1 - I

A(k,r)=Id(i,j); % I

fin pour

fin pour

fin pour

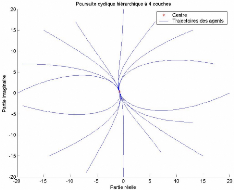
FIG. 3-2 - 16 agents dans une poursuite cyclique hiérarchique à 4 couches

fin.

Sous Matlab, nous avons obtenu la courbe dans la figure 3-2 traçant les trajectoires des agents dans une poursuite hiérarchique à L = 4 couches, et n = 16 agents.

Poursuite cyclique à L liens Ce schéma est aussi résolu avec l'équation 3.1, et la matrice correspondante AL est calculée à partir de la formule 2.17. L'algorithme qui implémentera cette méthode sera le même que la méthode précédente, et un pseudo code sous matlab décrivant la fonction de calcul de la matrice AL est la suivant :

Code 3.2

Début

A=zeros(n,n); % Initialisation de la matrice

pour k=0 à n-1

r = (k+1) mod n;

A (k, k) =-L ;

pour cpt=0 à L-1

r = (r+cpt) mod n;

A(k,r2)=1;

fin pour

fin pour

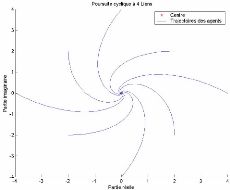
FIG. 3-3 - 8 agents dans une poursuite cyclique à 4 liens

A=(1/L) *A Fin.

Le graphe traçant les trajectoires d'un groupe de 8 agents effectuant une poursuite cyclique à 4 liens est dans la figure 3-3.

Rapetissement de polygone

Dans cette approche, à chaque instant "t", la position d'un agent est calculée à partir des positions précédentes de ses deux agents voisins. L'algorithme suivant trace les trajectoires des agents utilisant la technique de la courbure de Menger-Melnikov ou celle du schéma linéaire. Il est le même pour les deux méthodes, la différence réside dans le calcul de la fonction C de la formule 3.2. La résolution se fait toujours en utilisant la méthode de Runge Kutta.

z_ = C(zi_1,zi,zi+1) (3.2)

Algorithme 3.4

De but

% n est le nombre d'agents

% z est un tableau contenant les positions des agents à l'instant t % zprec est le tableau qui contient les positions à l'instant t-1

% zn est le centre des agents

zn = mean(z) % la moyenne du tableau z

h = 0.1;

Tant que (toutes les positions =6 centre)

pour chaque agent

zprec(i) = z(i);

w1 = Ci( zprec(j), zprec(i), zprec(k));

w = Ci( zprec(j)+(h/ )*w1, zprec(i)+(h/ )*w1, zprec(k)+(h/ )*w1);

w3 = Ci(zprec(j) + (h/ ) *w , zprec(i) + (h/ ) *w ,zprec(k) +(h/ ) *w );

w4 = Ci(zprec(j)+h*w3, zprec(i)+h *w3,zprec(k)+h*w3);

z(i) = zprec(i) + ((h/6) * (w1 + *w + *w3+w4));

finPour

fin tant que

fin.

Rapetissement par Menger-melnikov Pour cette méthode, comme nous avons vu au chapitre précédent la fonction C est calculée comme suit :

(zi_1 - zi - zi+1 - zi ) 1

ci(zi_1, ^zi, zi+1) = zi_1 - zi zi+1 - zi zi_1 - zi+1

Nous traçons alors le graphe qui décrit le rapetissement du polygone formé par les agents, ainsi que les trajectoires accomplies par les agents lors de leur convergence au centre. Voir la figure 3-4

Schéma linéaire Dans ce cas, la fonction C est définie comme suit, et les trajectoires, tracées par 16 agents mobiles effectuant un rapetissement de polygone, sont dessinées dans la figure 3-5:

1 1

ci(zi_1,zi,zi+1) = ₂(zi+1 ^-zi)+ _{2(zi_1} -zi)

Remarque 3.2 Les graphes seront commentés au chapitre suivant, où nous donnerons tous les résultats déduits sous Matlab, en parallèle avec ceux obtenus par la simulation.

3.3 Mise en oeuvre de la simulation

Dans cette perspective, nous réalisons notre simulation sous forme d'une applet java, une interface graphique qui permet de contrôler les entrées nécessaires au lancement de la simulation, de visualiser le comportement des agents dans un écran de simulation, ainsi que d'afficher les résultats déduits.

MengerMelnikov

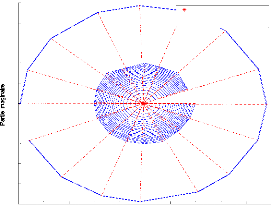
50

Centre

Rapétissement de polygone Trajectoires

30

20

10

40

0

10

20

30

40

50

50 40 30 20 10 0 10 20 30 40 50

Partie réelle

FIG. 3-4 - Rapetissement par Menger-Melnikov d'un polygone formé par 16 agents

Schéma linéaire

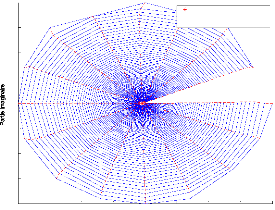
20

Centre

Rapétissement de polygone Trajectoires

10

5

15

0

-5

-10

-15

-20

-20 -15 -10 -5 0 5 10 15 20

Partie réelle

Nos robots autonomes et homogènes sont modélisés via des agents réactifs. L'espace dans lequel ces agents errent est sous forme d'un plan à deux dimensions considéré sans obstacles.

3.3.1 Cahier de charge du simulateur

la simulation va nous permettre de tester la validité des solutions proposées dans le chapitre 3, de suivre et de vérifier le comportement des agents dynamiquement et de mesurer certains facteurs d'évaluation qui permettent de comparer entre les différentes méthodes étudiées au chapitre précédent.

L'utilisateur doit avoir la possibilité de :

- Choisir la stratégie ainsi que la méthode qu'il désire tester,

- Introduire le nombre d'agents qui constitue le système, ainsi que les différentes entrées nécessaires à chaque méthode,

- Spécifier une précision qui représente à quelle distance les agents doivent se réunir. Si cette précision est nulle, les agents effectuent un rendez-vous au centre,

- Lancer la simulation, avec la possibilité d'arrêter et de reprendre l'exécution ainsi que de l'annuler,

- Visualiser les résultats de chaque simulation après son achèvement, stocker ces résultats qui représentent le temps de convergence et la vitesse moyenne des agents, ainsi que le nombre de senseurs nécessaires à la méthode,

La possibilité d'afficher un rapport final regroupant les résultats obtenus utilisant les différentes méthodes, et de calculer les rapports de taux vus au chapitre précédent.

3.3.2 Conception du simulateur

Avant de réaliser la simulation, et indépendamment du langage utilisé, nous allons d'abord passer par une étape de conception de notre système multi-agents en réalisant des modèles UML [14], pour décrire l'aspect statique et dynamique de l'application.

Définition 3.2 La conception consiste à apporter des solutions techniques aux descriptions définies lors de l'analyse, on y définit les structures et les algorithmes sans tenir compte du langage de programmation utilisé. Aujourd'hui, le standard industriel de modélisation objet est UML (Unified Modeling Language). UML unifie à la fois les notions et les concepts orientés objet, et aussi les notations nécessaires aux différentes activités d'un processus de développement et offre, par ce biais, le moyen d'établir le suivi des décisions prises depuis l'expression des besoins jusqu'au codage.

Dans ce qui suit, nous donnerons les diagrammes de conception de la simulation.

Remarque 3.3 Dans notre projet, il s'agit de modéliser un système multi-agents, or UML utilise une approche orientée objets. Nous définissons un agent comme étant un objet intelligent capable de prendre des décisions sans intervention externe, ainsi les vocabulaires d'agent, de composant ou d'objet peuvent être employés dans les divers contextes et domaines du coté de l'utilisateur. Alors que du coté du développeur, il y a un lien évident entre ces entités et il est même souhaitable d'uniformiser les descriptions pour ne pas avoir à employer des méthodes ou des formalismes différents.

Il n'existe pas moins de 12 diagrammes UML, partagés en deux vues, une statique et l'autre dynamique. Nous utiliserons seulement deux, chacun décrivant une vue pour modéliser notre système. Ces diagrammes ont été conçus avec l'outil UMLEclipse de l'éditeur Java Eclipse.

Modélisation structurelle

Pour donner une vue statique du système c'est-à-dire représentant le système physiquement, nous donnons le diagramme de classes (voir la figure 3-6), qui est le point central dans le développement orienté objet, il représente la structure du code orienté objet, et par la suite les modules qui constituent l'application. Une classe est décrite par son nom, ses attributs (propriétés) et ses méthodes (fonctions). Mentionnons que notre interface hérite de la classe Applet et implémente la classe Runnable (Thread). Ceci pour permettre à l'utilisateur d'interrompre son exécution à n'importe quel instant, modifier la vitesse de simulation, et ceci se traduit par un pseudo-parallélisme dans l'exécution.

Légende du diagramme de classes

Définition 3.3 En Java:

Fonction (variable) publique : c'est une fonction (variable) qui peut être appelée à partir d'autres classes du même package.

Fonction (variable) privée : ne peut être que par la classe mère, et les classes parentes.

Fonction synchronisée : désigne une fonction partagée par plusieurs threads, rendre une fonction de type "synchronized" fait qu'elle ne puisse être appelée que par un seul thread à la fois.

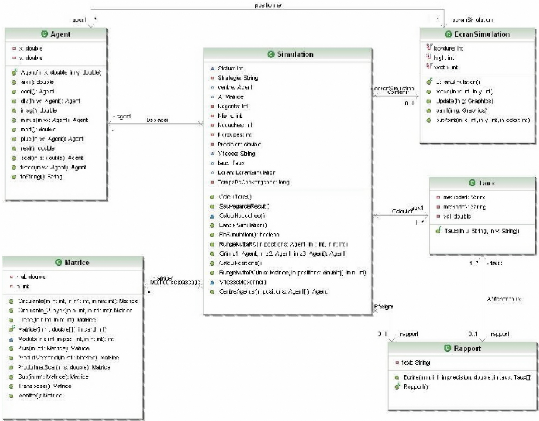
FIG. 3-6 - Diagramme de classes

1 V= n

Xn i=1

( di temps) (3.3)

Description des classes

La classe Simulation Représente l'interface principale de notre simulation, elle héritera dans la phase de réalisation de la classe Java Applet de la bibliothèque Swing. Cette classe regroupe les différents attributs et méthodes nécessaires à la réalisation des simulations, dont :

Les attributs :

- Le nombre d'agents dans le système,

- Le nombre de couches dans le cas d'une poursuite cyclique hiérarchique,

- Le nombre de liens dans le cas d'une poursuite cyclique à liens,

- Le nombre de groupes dans le cas d'une poursuite cyclique hiérarchique à deux couches, - Les positions des agents tout au long de la simulation,

- La précision telle que nous l'avons définie précédemment.

Les méthodes :

- _{Ci(zi_1,} ^zi, zi+1) : la fonction utilisée dans le rapetissement de courbe, décrivant l'évolution des agents du système.

- RungeKuttaPC() : pour la résolution de l'équation qui décrit le système dans le cas d'une poursuite cyclique.

- RungeKuttaRC() : La résolution de Runge kutta dans le cas du rapetissement de courbe.

- FinSimulation() : Une fonction booléenne qui scrute la fin de la simulation, autrement dit la réunion au centre.

- CalculNcouches() : Une fonction permettant le calcul des nombres de couches (L) admissibles en fonction du nombre d'agents saisi. La simulation permet d'effectuer les poursuites cycliques hiérarchiques :

- à 2 couches, avec possibilité de contrôler le nombre d'agents dans chaque groupe.

- Le cas optimal du schéma général, tel que nous l'avons vu auparavant, c'est à dire lorsque

pNL

2 N. Dans cette fonction, il s'agit de retrouver tous les L valides tels que cette condition L
soit vérifiée.

- CalculPositions() : Calcule les positions des agents dans le temps jusqu'à l'arrivée au centre et qui fait appel aux fonctions RungeKutta().

- CentreAgents() : Retourne les coordonnées du centre des agents.

- VitesseMoyenne() : Retourne la vitesse moyenne des agents, un facteur d'évaluation entre les différentes méthodes.

di : la distance parcouru par l'agent i.

temps : Le temps de convergence. C'est à dire, le temps nécessaire à l'accomplissement du rendez- vous.

- SauvegarderResult() : Une fonction qui permet de stocker les résultats obtenus (temps de convergence, vitesse moyenne, nombre de senseurs) des différentes méthodes, pour un nombre d'agents donné, afin de pouvoir les comparer. Les résultats ne sont sauvegardés que si cette simulation n'a jamais été lancée.

- CalculTaux() : Calcule l'augmentation dans les taux de convergence entre les différentes méthodes de la poursuite cyclique, ceux que nous avions approximé au chapitre 2. Le taux est calculé dans les cas que nous avons déjà vus.

La classe EcranSimulation Regroupe les propriétés de l'écran d'affichage des simulations, ainsi que des fonctions graphiques permettant son affichage, sa mise à jour ...

Les attributs :

- hight et width : décrivent les dimensions de l'écran.

- bordure : l'épaisseur de la bordure.

Les méthodes :

- paint() : la méthodes qui permet d'initialiser et d'afficher l'écran de simulation.

- Update() : met à jour l'écran, en affichant les nouvelles positions des agents ainsi que le centre. Elle est appelée par la classe Simulation.

- putPoint() : dessine un point (représentant un agent) su l'écran.

- Move() : la fonction qui gère le curseur, pour récupérer sa position d'où celle de l'agent à placer.

La classe Agent Comme chaque agent est représenté par sa position sous forme d'un nombre complexe, cette classe regroupera les propriétés et les fonctions qui gèrent les nombres complexes, telles que :

Les attributs :

x, y : la partie réelle et imaginaire du nombre complexe, représente aussi les coordonnées d'un agent selon l'axe des abscisses et des ordonnées.

Les méthodes :

- real() et imag() : retournent la partie réelle et imaginaire d'un nombre complexe. - mod() : retourne le module d'un nombre complexe, représente la vitesse d'un agent. - conj (): retourne le conjugué complexe d'un nombre complexe.

- plus(), minus(), times(), div (), scal() : les opérations effectuées sur les nombres complexes telles que : l'addition, la soustraction, le produit, la division ainsi que la multiplication par un réel.

La classe Matrice Une classe regroupant un ensemble de fonctions pouvant être effectuées sur des matrices carrées telles que : l'addition, la soustraction, le produit vectoriel, ... mais aussi des fonctions complexes telles que la construction d'une matrice circulante de dimension donnée.

Les attributs : Sont la matrice elle même (mat) et sa dimension (n).

Les méthodes :

- Identite() : Retourne la matrice identité de dimension n.

- Sub(), Plus (), ProduitVectorielCarre() : retournent les résultats de l'addition, la différence, et le produit vectoriel de 2 matrices carrées.

- ProduitMatScal() : retourne une matrice qui résulte produit d'un nombre réel par la matrice mat.

- SommeV() : somme de deux vecteurs.

- Modulo(i, pas, n) : retourne le résultats de (i + pas) mod n.

- Circulante(m, n1, n_m) : une fonction récursive qui calcule la matrice circulante décrite dans la formule 2.15. avec m est le nombre de couches, n1 le nombre d'agents de la première couche, et n_m le cardinal de chaque couche.

Circulante(n, n1) : un cas particulier de la matrice circulante qui est celle de la poursuite cyclique hiérarchique à deux couches, deux attributs sont nécessaires dont le nombre d'agents total et le nombre d'agents de chaque groupe, calculé à partir du nombre de groupes.$ Lliens(L, n) : retourne la matrice circulante de la poursuite cyclique à L liens, telle qu'elle est décrite dans la formule 2.17.

La classe Taux Cette classe représente les rapports de taux entre les différentes méthodes de la poursuite cyclique.

Les attributs : meth1 et meth2 pour décrire les deux méthodes comparées, et val la valeur du rapport approximé précédemment.

Les méthodes : Taux(meth1, meth2) : le constructeur de la classe.

La classe Rapport Cette classe représente une fenêtre (Frame) indépendante qui affiche le rapport regroupant les différents résultats obtenus lors des simulations lancées pour un groupe d'agents donné.

Les attributs : seulement un champs de texte qui affiche le rapport.

Les méthodes :

- Initialize() : réinitialisation du champs de texte, par exemple après changement du groupe d'agents.

- Ecrire() : Ecrit un rapport dans le champs de texte qui contient : le temps de convergence, le vitesse moyenne et le nombre de senseurs de toutes les simulations, ainsi que les rapports calculés entre les différentes méthodes de la poursuite cyclique.

Modélisation comportementale

Nous avons choisi le diagramme de séquences (voir figure 3-7), pour modéliser la vue dynamique de la simulation, montrer son fonctionnement et l'interaction entre l'utilisateur et l'interface de simulation.

3.3.3 Réalisation de l'interface graphique

Nous avons réalisé notre simulation sous forme d'Applet héritant de la classe JApplet de la bibliothèque Swing. L'interface graphique a été implémentée avec le plugin Visual Editor de l'EDI (Environnement de développement intégré) Java [15, 16, 17] Eclipse 3.2.

Définition 3.4 Les Swing sont des composants (boutons, fenêtres, label, menus ...) utilisés pour faire des interfaces graphiques. Ces composants sont regroupés dans le package Swing. Eclipse 3.2 comporte par défaut ce package.

Remarque 3.4 Les nombres manipulés dans la simulation sont tous des réels de format double, le type de codage est : IEEE 754.

L'interface de simulation est présentée dans la figure 3-8.

1 : Un bouton permettant l'affichage du rapport des résultats de la simulation.

2 : Onglets des entrées de la simulation, des deux stratégies et selon la méthode sélectionnée. Les champs doivent contenir des nombres positifs.

3 : L'écran de simulation, les robots mobiles sont représentés par des points de masses.

4 : Permet de contrôler la vitesse de simulation.

5 : Les résultats de la simulation, contient un chronomètre qui calcule le temps de convergence, et affiche à la fin de simulation la vitesse moyenne des agents donnée par l'équation 3.3. Ainsi que le nombre de liens de communication (senseurs) dans le système nécessaires à l'accomplissement de la stratégie.

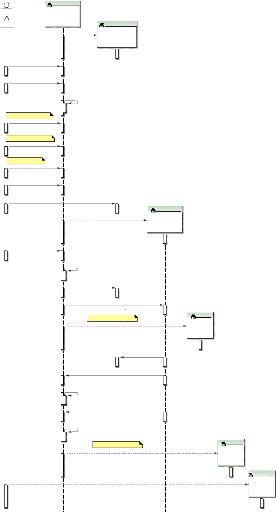
Utilsateur

setPrecision()

Donner uneprécision deconvergence

Si méthode = PC hiérarchique

Si le nombredecouches est2

Si méthode = PC à liens

Choisir la s tratégieetla méthode

setNgroupes()
Sais ir le nombredegroupes

Choisir Nombre decouches

Sasir le nombre d'agents

Sais ir lenombre de liens

Lanc er la s imulation

LancerSimulation()

setN couches ()

Selectionner()

setNagents()

setNliens()

Positionner les agents

Interface:Interface

putPoint()

Ec ranSimulation()

Initialier Ec ran

Calculer les nombres de couches possibles

CalculNcouches()

Calc ulerla positionducentre

CalculCentre()

Afficher le temps de simulation Calc ulTemps ()

Sauv egarder les résultats Sauv egarderResult

Afficher le centre

putPoint()

La position des agents atteintle centre

Si méthode = Pours uite cy clique

Affichervitessede c onvergence

Calc uler lesnouvelles positions

Créer les agents

Si méthode = pours uite cy clique

Afficher le rapportdes résultats des s imulations

Vites seDeConvergence()

Agent()

Calc uler la matricede transformation

CalculPositions()

Ec ran: EcranSimulation

FinSimulation()

Circ ulante()

Afficher les nouvelles pos itions

Calc uler les rapports de taux

Ec rire()

Calc ulTaux()

Update()

PosAgent:Agent

A:Matrice

Taux :Taux

Rap port: Rappo

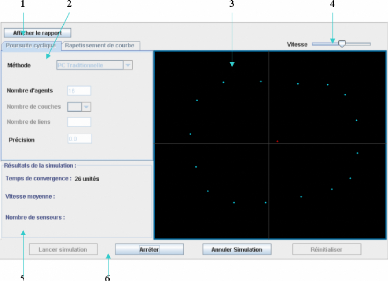
FIG. 3-8Interface principale de la simulation

6 : Boutons de contrôle, permettant de lancer la simulation, l'arrêter puis la reprendre, l'annuler ou de tout réinitialiser.

Remarque 3.5 Le temps de convergence:

Représente le nombre d'unités de temps nécessaires à l'accomplissement du rendez-vous. L'unité est le pas de la méthode de Runge Kutta, que nous avons vu au chapitre 3, et qui est égale à h = 0.1.

L'applet permet de tester les différentes stratégies étudiées dans le chapitre 2, et de percevoir le comportement des agents réalisant une stratégie de rendez-vous sans l'intervention de l'utilisateur entre le lancement et l'accomplissement de la simulation. Un rapport (voir la figure 3-9), sous forme d'une Jframe avec un bouton fermer, peut être visualisé à la fin de chaque simulation, regroupant tous les résultats obtenus, pour un groupe d'agents donné, et aussi les rapports de taux calculés entre les méthodes de la poursuite cyclique et qui permettent de comparer entre elles. Dans l'exemple de la figure, le résultat du rapport de taux entre la poursuite cyclique hiérarchique à 4 couches et la traditionnelle signifie que la première converge 64 fois plus rapidement que la seconde.

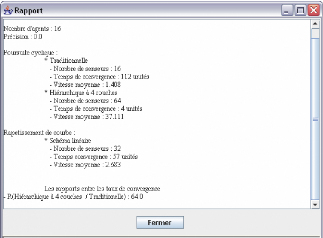
FIG. 3-9 - Rapport des résultats

3.4 Conclusion

Dans ce chapitre, une implémentation des approches de la stratégie de Rendez-vous, présentées dans le chapitre précédent, a été réalisée. Une première étape fut la vérification et la validation des algorithmes de base sous matlab, la seconde fut la mise en oeuvre d'une simulation Java implémentant toutes les méthodes, simulant la coopération et le déplacement des robots autonomes et affichant les résultats que nous allons discuter au chapitre qui suit, et qui va résumer l'ensemble des conclusions, des remarques et des théories fondées.

Le passage par Matlab fut très bénéfique dans le sens où ceci nous a permis une facilité dans la conception des algorithmes sans devoir programmer les outils mathématiques nécessaires à notre étude. La deuxième partie nous a permis de nous familiariser avec le langage de programmation orienté objet Java et plus spécialement avec l'environnement Eclipse, qui nous a aussi facilité l'étape de conception avec son plugin UMLEclipse.

Chapitre 4

Résultats et discussions

Dans ce chapitre, nous présenterons un résumé des résultats, des remarques et des conclusions obtenues lors de notre travail pratique qui a été abordé au chapitre 3. Nous discuterons des différents problèmes rencontrés lors de l'implémentation de la stratégie de rendez-vous et comparerons entre les méthodes étudiées pour réaliser cette stratégie.

Le chapitre se compose de deux parties, la première concerne le tracé de graphes sous Matlab en vue de comparer les trajectoires dessinées par les agents utilisant les trois méthodes de la poursuite cyclique, et celles du rapetissement de polygone et l'influence des nombres (de couches ou de liens) sur les vitesses de convergence.

Dans la seconde, nous allons commenter le comportement des agents qui a été observé lors des tests de simulations sous différentes approches, dans le but de déceler les avantages et les inconvénients des unes et des autres.

4.1 Résultats obtenus sous Matlab

4.1.1 Comparaison entre les méthodes

Hormis les trajectoires des agents tracées aux chapitre 3 (voir figures 3-1, 3-2, 3-3, 3-4, 3-5) pour vérifier leur convergence au centre, nous allons tracer dans cette partie d'autres graphes, les premiers affichent une comparaison entre les différentes méthodes, et les autres consistent à augmenter les nombres de (couches/liens) et à percevoir l'impact de ceci sur la rapidité de convergence.

Comparaison entre les méthodes de la poursuite cyclique

Nous avons tracé dans le même graphe (sur la figure 4-1) les 3 courbes décrivant les trajectoires des agents utilisant les méthodes de la poursuite cyclique, afin de pouvoir comparer entre elles.

Les 3 méthodes de la poursuite cyclique

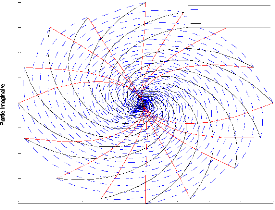
20

Traditionnelle Hiérarchique 4-couches Hiérarchique 4-liens

10

5

15

0

-5

-10

-15

-20

-20 -15 -10 -5 0 5 10 15 20

Partie réelle

FIG. 4-1Les 3 méthodes de la poursuite cyclique d'un groupe de 16 agents

Nous remarquons que, les agents avec la méthode hiérarchique à 4 couches convergent au centre en premier, suivi de la poursuite cyclique à 4 liens, puis de la traditionnelle qui est la plus lente, ce qui confirme les résultats obtenues théoriquement au chapitre 2 en référence à ceux de Smith [1]. Sachant que les deux premiers schémas utilisent le même nombre de senseurs.

Comparaison entre les méthodes du rapetissement de polygone

Les trajectoires des agents qui s'affichent en bleu sur la figure 4-2 sont celles tracées en employant le schéma linéaire, les agents convergent effectivement et rapidement au centre en effectuant un rapetissement du polygone formé par les 16 agents. Par contre, dans le cas du rapetissement de Menger-Melnikov, nous remarquons que les agents se rapprochent, donnant l'illusion qu'ils convergent au centre, puis d'un seul coup s'éloignent comme il est montré sur les figures 4-2 et 3-4 ce qui va être mieux visualisé sur la simulation. Ceci est dû particulièrement au fait que lorsque les agents se rapprochent, la formule 4.1 va tendre vers l'infini, puisque les dénominateurs tendent vers 0. Ainsi, les positions des agents se dirigent dans le sens contraire et s'éloignent de leur lieu de rendez-vous, que nous allons voir dans la simulation qu'il ne se situe pas toujours au centre!

(zi_1^-zi_- zi+1 - zi ~ 1

ci = c(zi_1; ^zi; zi+1) = (4.1)

zi_1 - zi zi+1 - zi zi_1 - zi+1

trajectoires des méthodes du rapetissement de polygones

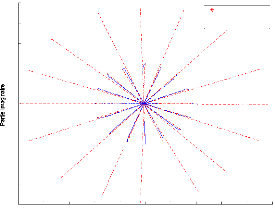
Centre MengerMelnikov Schéma linéaire

40

30

20

10

0

10

20

30

40

50

50 40 30 20 10 0 10 20 30 40 50

50

Partie réelle

FIG. 4-2Trajectoires des deux méthodes du rapetissement de polygone

Le problème de Menger-Melnikov sera étudié plus en détail dans les résultats de la simulation.

4.1.2 Mise à l'échelle du nombre de couches dans un schéma hiérarchique

Dans la figure 4-3, nous avons voulu tester l'influence de l'augmentation du nombre de couches sur la vitesse de n = 16 agents et leur convergence au centre. Il s'est avéré que lorsque le nombre de couches augmente, la stratégie de rendez-vous s'effectue plus rapidement. Car la PC hiérarchique à 4 couches (n1 = n2 = n3 = n4 = 2) est plus rapide que celle à 2 couches (n1 = 2, 8 groupes), ainsi que celle à une couche.

4.1.3 Mise à l'échelle du nombre de liens dans un schéma à L liens

De la même manière, nous montrons que lorsque le nombre de liens dans une poursuite cyclique à L-liens augmente, la convergence au centre des agents se fait plus rapidement. Ceci est affiché sur la figure 4-4.

4.2 Résultats de la simulation

La poursuite cyclique hiérarchique

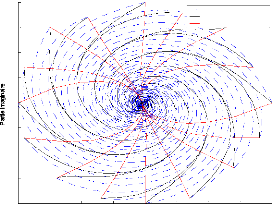
20

1 couche (traditionnelle)

2 couches
4 couches

10

5

15

0

-5

-10

-15

-20

-20 -15 -10 -5 0 5 10 15 20

Partie réelle

FIG. 4-3 - La poursuite cyclique hiérarchique de 16 agents en fonction du nombre de couches.

Poursuite cyclique à Liens

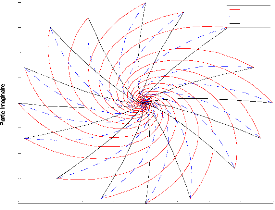
4 liens 8 liens 12 liens

10

5

0

-5

-10

-15

-20

-20 -15 -10 -5 0 5 10 15 20

20

15

Partie réelle

par la simulation (temps de convergence, vitesse moyenne des agents, nombre de senseurs et les rapports entres les taux de convergence).

4.2.1 Poursuite cyclique

Notre simulation permet de visualiser les agents autonomes, dotés de senseurs omnidirectionnels représenté par des points de masses et effectuant une poursuite cyclique, pour se réunir en vain au centre de rendez-vous. La poursuite cyclique a été réalisée par les trois méthodes étudiées dans les chapitres 2 et 3. Nous avons pu déceler quelques règles via les simulations de ces trois méthodes pour quelques configurations d'agents dont :

Les agents convergent, dans tous les cas, au centre de consensus sans jamais se heurter. Ceci confirme la validité des résultats obtenus par la synthèse théorique et les graphes tracés sous matlab.

Le temps de convergence des agents augmente, et la vitesse moyenne diminue quand le nombre d'agents est grand dans une poursuite cyclique.

- Le temps de convergence dans un schéma hiérarchique est toujours plus petit, suivi de celui à L liens, et finalement par la poursuite cyclique traditionnelle. Contrairement à la vitesse de convergence qui augmente.

- Dans une poursuite hiérarchique, le temps de convergence est proportionnel, et la vitesse est inversement proportionnelle au nombre de couches. Cependant, quand ce dernier est grand, le nombre de liens de communication concrétisés par des capteurs, augmente. Mais ceci se traduit aussi par une augmentation dans la complexité de calcul, et de traitement.

- De même pour le schéma à L liens, la convergence est d'autant plus rapide que le nombre de liens augmente, c'est même la solution qui converge le mieux sous la condition 4.2 :

Nombre de liens = Nombre d^'agents - 1 (4.2)

- Les rapports entre les taux de convergence, approximé dans le chapitre 2, signifient combien de fois une méthode est plus rapide que l'autre. Dans les résultats obtenus, La PC hiérarchique à L couches est N1 fois plus rapide que la PC à L liens qui est elle même N2 fois plus rapide que la PC traditionnelle. Avec N1 > N2.

Ceci dit, nous avons pu aussi déduire quelques inconvénients de cette stratégie notamment en ce qui concerne le comportement des agents. Ces derniers empruntent un chemin très long pour atteindre le centre au même moment.

FIG. 4-5 - Le comportement observé des agents avec la méthode de Menger-Melnikov

En ce qui concerne la PC hiérarchique, la configuration n'est possible que dans certains cas, notamment lorsque ^LpNL est un entier ou lorsque le nombre de groupes est valide quand c'est un schéma à deux couches.

4.2.2 Rapetissement de polygone

Cette approche possède l'avantage d'exiger un nombre fixe de capteurs et le même pour les deux méthodes et qui équivaut à 2n. Ce qui facilite la possibilité de les départager. Durant notre étude, certaines remarques et déductions ont été faites :

- Dans le schéma linéaire, la dynamique du rapetissement s'effectue normalement et les agents convergent dans une durée raisonnable.

- Dans la méthode de la courbure de Menger-Melnikov, nous avons observé une dynamique étrange du rapetissement de polygone et donc de la convergence des agents. Ceux-ci se rapprochent au début très lentement. Ensuite les vitesses s'amplifient infiniment jusqu'à ce qu'ils se réunissent à un point qui ne se situe pas forcément au centre de gravité. Les agents aussi se heurtent quand ils sont trop proches, ce comportement inconvenable, vu risqué, est exposé sur la figure 4-5 :

Solution:

En tentant de faire converger les agents au centre, nous ne pouvons ignorer le fait que les agents se rentrent dedans, ce qui est dangereux. La seule solution que nous avons pu apporter à notre simulation est d'arrêter celle-ci dès que les agents sont trop proches les uns des autres, en remplaçant le test d'arrêt qui est l'arrivée des agents au centre par la nullité des dénominateurs

de la formule 4.1. La vitesse de convergence n'est pas calculée dans ce cas, puisque les agents n'atteignent pas le centre.

Et comme l'un des objectifs majeurs de la simulation est de tester la validité des solutions proposées théoriquement, cette stratégie a été classée instable et donc inappropriée.

- Nous avons aussi remarqué que dans les deux méthodes du rapetissement de polygone, les agents disposés n'importe comment forment d'abord une sorte de polygone convexe dont les sommets sont ces agents, puis effectuent le rapetissement au centre en forme d'ellipse.

4.2.3 Remarques

Nous avons pu faire d'éventuelles observations et proposé des solutions lors de notre étude, et qui sont:

- En comparant entre les deux approches, nous avons remarqué que le schéma linéaire effectue une convergence directe au centre, sans faire de détour, par contre les déplacements des agents sont relativement petits comparés à ceux de la poursuite cyclique. Donc, le schéma linéaire converge plus rapidement que la PC traditionnelle mais moins que le schéma hiérarchique et celui à L liens.

- L'un des inconvénients de notre implémentation est que les agents agissent dans l'ordre d'entrée, plus précisément dans la poursuite cyclique. La solution à apporter serait de renuméroter ces agents selon leurs positions et d'économiser ainsi des déplacements inutiles des agents.

- Les agents ne perçoivent pas le lieu de rendez-vous, ce qui fait que dans certaines situations, nous avons remarqué que les agents passent prés du centre sans s'arrêter, poursuivent leur stratégie puis retournent au même point. Une solution serait d'ajouter des senseurs pour dédecter l'approche du point de rendez-vous et s'arrêter dès que celui-là est atteint, dans le cas où l'arrivée au même moment de tous les agents n'est indispensable.

4.3 Conclusion

Au cours de ce chapitre, nous avons réussi à résumer les différentes remarques et observations établies durant les nombreuses simulations que nous avons testées et les graphes de trajectoires que nous avons tracés sous Matlab, afin de détecter le comportement des agents et pouvoir comparer entre les méthodes de la stratégie de rendez-vous.

Une conclusion a été déduite concernant le rapetissement par la courbure de Menger-Melnikov qui a engendré des résultats inattendus et peu satisfaisants qui ne correspondent pas à la stratégie voulue. Cette méthode a été classée inutilisable vu les inconvénients qu'elle présente.

Conclusion générale

L'objectif principal du travail décrit dans ce mémoire était d'appliquer les théories de la poursuite cyclique et du rapetissement de courbe au problème de la stratégie de rendez-vous dans les systèmes multi-agents.

Une première partie fut l'initiation et la compréhension de ce domaine des SMA, et plus particulièrement à son application aux groupes de robots mobiles et à la stratégie de rendez-vous.

A titre préparatoire, nous avons mis en oeuvre les algorithmes des solutions proposées sous Matlab; une étape qui fut à la fois simple et importante à la compréhension du comportement d'agents et l'optimisation des algorithmes. Nous avons également réalisé une interface graphique sous Java pour la simulation du comportement des agents utilisant les différentes approches pour effectuer la stratégie précitée et qui nous a permis d'évaluer certaines valeurs de convergence, afin de comparer entre ces méthodes.

Au cours des tests de simulation, nous avons éliminé la méthode de la courbure de MengerMelnikov qui a révélé un comportement inadapté à la stratégie du rapetissement de courbe et au problème de rendez-vous.

Ce travail accompli pourrait servir à implémenter l'autre stratégie de Smith qui est la stabilisation à une formation où un groupe d'agents mobiles doit être stabilisé pour former les sommets d'un polygone équilatéral et où le centre de gravité du polygone reste statique pendant l'évolution. On pourrait aussi déplacer le centre des agents et créer ainsi une stratégie de navigation du groupe mené par un agent leader positionné au centre qui sera dynamique.

Bibliographie

[1] Stephen L. Smith. «Strategies for RendezVous and Formation stabilization of Multi-Agents Systems », University of Toronto, 2005

[2] J. ferber « Les systèmes multiagents vers une intelligence collective » Lien : http : // jbenech.free.fr/old_site/agents/html/P-definition.html

[3] Lemlouma Tayeb, Boudina Abdelmadjid. «L'intelligence Artificielle Distribuée et les systèmes multi-agents »

[4] Drogoul, A.; Corbara, B.; Lalande, S. 1995. "MANTA : New Experi-
mental Results on the Emergence of (Artificial) Ant Societies", Lien : http : // www.limsi.fr/'jps/enseignement/examsma/2003/ISRAEL _GAUCHOU/SMA.html

[5] C.W.Raynolds, «Flock, heard and scools : A distributed behavioral mode.», http :// www.red3d.com/cwr/boids/

[6] Marc Côté et Nader Troudi, NetSA : "Une architecture multiagent pour la recherche sur Inter- net" Département d'Informatique, Université Laval

[7] La norme ISO 8373(1994)

[8] M.Mataric, « Designing emergent behavior : From local interaction to collective intelligence », Lien : http :// www.complexity.org.au/ci/draft/draft/schaef0 1/schaef01s.ps

[9] Projet mars explorer de l'équipe SMAC, l'IUT d'Informatique de Lille I, Lien : http :// www2.lifl.fr/~secq/projects/mars/site/

[10] P.R Lascaux. Théodor, «Analyse numérique matricielle appliquée à l'art de l'ingénieur.», Dunod, 1994

[11] A.M. Bruckstein, N. Cohen, and J.J. Gray. Geometry. Cambridge University Press, 1999.

[12] Jean Frédéric Frenet, Lien : http :// fr.wikipedia.org/wiki/Rep%C3%A8re_de_Frenet

[13] M.Mokhtari, Matlab 5.2 & 5.3 et Simulink 2 & 3 pour étudiants et ingénieurs, Edition Springer_Verlag Berlin Heidelberg, 2000.

[14] Grady Booch , James Runbough, Ivar Jacobson, «UML, Le guide de l'utilisateur», Paris Eyrolles, 2001

[15] Bruce Eckel, «Thinking in Java », Prentice Hall PTR ISBN 0-13-659723-8, 1998

[16] Robert Michel Di Scala, «L'essenteil de l'informatique et de la programmation», Algerie Edition BERTI, 2004

[17] David J. Eck, Introduction to Programming Using Java, Edition 5.0, 2006. Lien : http : // math.hws.edu/javanotes/