Systeme de transition sur les ordre Partiellement complet

1.4 Coproduit des opc s

Notre objectif est de déterminer le coproduit d'une famille d'opc^s. En s'inspirant de la construction des coproduits dans la caté_gorie ENS. Soit _(Ai)i?I une famille d'opc^s. Posons

_X A_i = {(a,i), a E A_i et i E I}

i?I

Munissons P i?I		Ai de la relation d'ordre définie par (a, i) (a', j) si et seulement si i = j et
a a'. Le lemme suivant permet de conclure que P i?I définies par : li (a) = (a, i), est le coproduit de la famille (Ai)i?I. Lemme 1.11. Soit (Ai)i?I une famille d'opc^s.			Ai, muni des injections li : Ai ? P i?I	Ai
i) P i?I	Ai muni de la relation ci-dessus définie est un opc.

ii) Les li sont continues

iii) Pour tout opc C et pour toute famille d'applications continues fi : A_i ? C, il existe

une unique application continue ? : P i?I

Ai ? C rendant commutatif le diagramme

suivant.

_P
i?I

ça

²²

C

A_i

~~}}}}}}}}}}}}}}}}}}

fi

li

A_i

Preuve. i) Montrons que P i?I

Ai est un opc. Soit D une partie dirigée de P i?I

Ai.

Pour tout (a, i) et (a', j) dans D, il existe (a», k) dans D tel _que (a, i) (a», k) et

(a', j) (a», k) d'après la définition de , i = k = j. Il s'en suit _que D est continue

dans une unique composante {i} x Ai de P i?I

Ai. D étant dirigé {a, (a, i) E D} est une

partie diri_gée de A_i.

i?I

On montre sans peine _que (V^Ai{a, (a, i) E D}, i) = VP Ai D.

ii) Montrons que les injections li : Ai ? P j?I

Aj sont continues.

Soit D une famille diri_gée de A_i. On a :

li (D) = {li (d), d E D}

= {(d, i), d E D}, donc

_P

VAj li (D) = VP

j?I j?I Aj {(d, i), d E D}

_P

= Vj?I Aj D x {i}

=V^AjDx {i}

VAi D )

= li

Donc li est continue.

iii) Montrons que P iEI

Ai possède la propriété universelle des coproduits. Soit C un opc. Soit

(fi) une famille d'applications continues de Ai dans C.

Considérons l'application ? : P jEI

A j ? C définie par ? ((a, j)) = fi (a). Les fi étant

continues, il en est de même pour ?. De plus cette application rend commutatif le dia_gramme suivant :

_P
iEI

ça

²²

C

A_i

~~}}}}}}}}}}}}}}}}}}

fi

_oo

li

A_i

.

Il reste à démontrer que ö est unique. Soit ø : P jEI

A j ? C rendant commutatif le

dia_gramme ci dessus. Pour tout (a, j) E P Aj

jEI

? ((a, j)) = ? o li (a)

= fi (a), par commutativité du dia_gramme

= øoli (a) = ø ((a, j))

donc ?= ø

Pour illustrer cette notion et faciliter sa compréhension, nous allons donner _quel_ques exemples.

_OO

_OO

(2,0)

(x,0)

1.4.1 Exemples de coproduits

i) Soient deux OPC^s R et T ci-dessous représentés

R = z qq

_{77 hh}

%%

x

3₃ y

_ee

Leur coproduit est représenté par :

R + T = (z,1)

₇₇

_gg

uu

<<

1₁ (y, 1)

(x,1)

zz

T= 2 qq x rr

^^>>>>>>>>

^ccGGGGG_GGGG

1 mm

_zmm

y _mm

uu

uu

_OO

(z, 0) LL

(y, 0) LL

(1,0) LL

ii) Posons A₂ = {2p, p = 8}. Munissons le de l'ordre <défini par 2ⁿ < 2^m si et seulement si n divise in. Il est clair _que A2 muni de cette relation est un opc. Munissons é_galement A2 de la structure d'opc définie par la relation d'ordre :

2n 4 2^m ssi n et in ont même parité et 2ⁿ = 2^m.

Le schéma de représentation du coproduit de ces deux opc est :

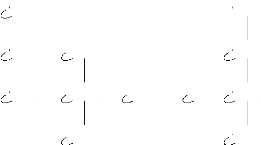
(2⁵, 0)

₇₇

(2⁴, 1)

(2⁶, 1)

₇₇

₇₇

_{OO :u:}

_uuuu^uuuu

_OO

(2⁷,0)

₇₇

(2⁸, 1)

_OO

₇₇ (2⁵, 1) ₇₇ (2⁷, 1)

_OO :u: 5j5

₇₇

(2², 1)

^ddIIIII_IIII

₇₇

(2³, 1)

₇₇

(2³,0)

₇₇

(2¹, 1)

₇₇

(2¹,0)

₇₇

(2⁴,0)

(2², 0)

₇₇

Pour tout x = y E S I_a ilexisteáEËtel_que(x = yEI_a)doncxEI_a ? S I_a

aEË aEË