Conclusion
Toutefois le taux de rentabilité est calculé
comme étant la différence entre deux cours, l'une initial et
l'autre finale rapporté au cours initial. La rentabilité d'un
investissement incertain exige des estimations probabilistes des états
de nature possibles ; c'est à dire que à chaque état de
nature on effectue une probabilité de réalisation d'un futur
incertain et par suite il faut choisir la distribution appropriée.
Ce chapitre décrit brièvement la théorie
du choix des portefeuilles, On a vu que les préférences d'un
investisseur peuvent être représentées par une fonction de
rendement espéré et la variance d'un portefeuille et que les
hypothèses de la théorie de l'utilité prévue
peuvent être violés systématiquement.
À la lumière de ces observations nous arguons du
fait que théorie de l'utilité, pendant qu'elle est
généralement interprétée et appliquée, n'est
pas à modèle descriptif proportionné.
Un investisseur averse au risque préfère un
rendement certain à n'importe quelle perspective risquée avec la
valeur prévue X. Dans la théorie de l'utilité
prévue, l'aversion de risque est équivalente à la
concavité de la fonction d'utilité, ce qui explique l'orientation
vers les actifs qui possèdent le risque le plus faible.
Or plusieurs études ont donné la preuve que dans
les choix risqué, les investisseurs tendent à surestimer la
probabilité des événements extrêmes et à
sous-estimer la probabilité des événements normaux.
On a cité que le concept d'aversion aux pertes se
repose sur deux résultats centrales, la première étant que
l'analyse des gains et des pertes est évalué relativement
à un point de référence neutre, et la deuxième,
porte sur les changements qui rendent une perte perçue de manière
deux fois plus déplaisant qu'un gain.
Markowitz condense l'optimisation de portefeuille en deux
stations ; dans un premier temps, on trouve la combinaison optimale d'actifs
risqués puis, on ajoute, à ce portefeuille optimal risqué,
une certaine proportion d'actif sans risque.
À travers une simple programmation quadratique
(minimiser la variance pour une rentabilité donnée), on
sélectionne les titres à mettre dans notre portefeuille sous deux
hypothèses, la première c'est la normalité des rendements
du portefeuille et la seconde c'est que la moyenne du rendement et sa
volatilité résument toute l'information nécessaire sur la
performance du portefeuille, mais aussi de son risque.
L'ensemble des solutions pour différents niveaux de
rentabilité constitue une série des portefeuilles dite efficients
et chaque investisseur, suivant son degré d'aversion au risque,
détermine le portefeuille optimal.
Introduction :
Le choix de portefeuille est basé sur un arbitrage
entre le rendement et le risque, à cet effet, plusieurs méthodes
de mesure de risque sont apparues depuis le début du
XXéme siècle dans le but d'évaluer le risque
simple et également le risque de perte: En effet, c'est Neumann et
Morgenstern qu'ont développé la première mesure de risque
fondamental qui est la volatilité. Mais, suite à des crashs
boursiers catastrophiques, d'autres mesures ont été
dévoilées. Toutefois, ces mesures ne donnent qu'une approximation
du risque. Pour cela les investisseurs ont recherché des nouvelles
stratégies pour assurer leurs portefeuilles. Parmi ces politiques, on
mentionne, la théorie de Safety-First de Roy (1952).
Néanmoins, l'utilisation des mesures de risque simples
est insuffisante dans certains cas, puisqu'elles ne tiennent pas compte des
pertes extrêmes qui peuvent conduire les investisseurs à des
pertes catastrophiques, voir même la banqueroute. A ce fait, et
après la crise boursière de 1987 qui a un effet négatif
sur l'accroissement de la volatilité, les gestionnaires de risque ont
élaboré un nouveau indicateur du risque financier qui est
à la fois globale et synthétique ; c'est la mesure de risque de
perte présenté en terme de la Value at Risk et la Value at Risk
conditionnelle.
De ce fait, nous déroulons ce chapitre en trois
sections : la première propose la notion de risque ainsi que la
définition d'une mesure cohérente. La seconde section est
consacrée à la présentation des mesures de risque simples
tel que les mesures de Downside et les mesures de dispersion. Dans la
troisième section, nous exposons la VaR et la CVaR comme mesure de
risque de perte dans la gestion de risque.
II.1 Mesure cohérente de risque
II.1.1 Notion de risque
En Tunisie tous comme à l'échelle
internationale, les institutions financières sont disciplinés par
une variété des risques qui sont généralement
classés sous quatre genres qui sont :
· Le risque de crédit : c'est
incapacité à respecter les engagements de régler les
dettes que se soient principale ou intérêt.
· Le risque de liquidité : ce type
de risque touche toute personne physique ou morale à cause de la
détention d'un actif peu liquide.
· Le risque de marché : ce type
de risque peut être résultat d'une évolution
défavorable des paramètres de marché, D'une manière
plus précise, c'est le risque de perte sur la position du bilan et du
hors bilan.
· Le risque opérationnel : c'est
l'ensemble des risques provenant d'erreurs dans le développement des
outils de valorisation ainsi que de défaillance de procédure, de
personne ou de système.
Se couvrir contre ces risques d'une part, et profiter d'une
situation propice d'autre part, sont les intérêts d'un
investisseur rationnel et l'accès à ces objectifs part par la
mesure de risque.
II.1.2 Notion de la mesure cohérente de
risque
Artzner et al (1997) ont définie une mesure
cohérente de risque en 1997 comme suite : une mesure ? : V
?R de risque s'appelle une mesure cohérente de risque si
elle satisfait les
quatre propriétés suivantes
- Invariance par translation : ?(X
+ á.r) =?(X) -
á
L'addition d'un montant sureá au portefeuille
initial réduit le risque globale d'un montantá.
- Homogénéité positive :
?(ëX) = ë? . ( X )
Le risque est proportionnel à la taille de la position X
pour tenir compte d'un éventuel risque de liquidation lorsque la taille
de X est grand.
- Sous-additive : ? Portefeuille X et Y,
?(X + Y) = ?(X)
+?(Y)
Cette propriété reflète le gain de la
diversification en matière de réduction de risque par le fait de
la corrélation entre les composantes de portefeuille.
- Monotonie : ? X et Y?V si X > Y donc
?(X)=?(Y)
Le risque a une fonction croissante avec la perte autrement dit
la position caractérisé par une perte plus élevé,
elle semble plus risqué.
II.2 Mesures de risque simples
Markowitz et Tobin (1959) ont montré qu'un investisseur
rationnel choisie un tel actif financier à partir deux épreuves ;
le rendement espéré et la variance de titre. Cependant, dans
certain cas ces deux critères sont insuffisants, à titre
d'exemple lorsque la variance et l'espérance rendent l'investisseur
indifférent entre deux titre ou plus.
Toutefois, Si on veut apprécier la performance d'un
actif financier et tenir compte de risque, l'investisseur doit calculer
correctement le risque de chaque titre de portefeuille qui veut construire.
À cet instar, il existe deux types des mesures de risque simples ; la
mesure de dispersion et la mesure de Downside.
II.2.1 Mesures de baisse ou de Downside
L'objectif de ces mesures est la maximisation de
probabilité pour que le rendement de portefeuille soit au-dessus d'un
certain niveau acceptable et minimal, souvent ce dernier est connu sous le nom
de Benchmark (1) ou le niveau de faillite.
II.2.1.1 Semi - Variance
Markowitz a proposé l'utilisation du semi - variance
dans le cas où l'investisseur est indifférent entre deux titres
ou plus après avoir calculer la variance, c'est-à-dire, la
variance est parfois insuffisante pour prendre la décision
adéquate.
À cet instar, la semi- variance, noté SV, est
défini comme l'espérance des carrés des écarts que
les valeurs d'un taux de rentabilité d'une action inférieure
à son espérance présentent par rapport à celle-ci
:
n
|
SV(R ) = p
i i
|
( ) 2
R i E R i
- ( )
|
|
avec Ri
|
i 1
=
< E(R )
i
|
(28)
|
Bien que cette mesure soit un remède dans le cas où
la variance est insuffisante pour choisir le portefeuille optimal, elle
néglige les rendements supérieurs à la moyenne E (Ri).
(1) Florin Aftalion « la nouvelle
finance et la gestion des portefeuilles»: « il existe des fonds qui
possèdent un Benchmark, c'est-à-dire un indice ou un portefeuille
dont la gestionnaire doit reproduire plus ou moins exactement la performance en
essayant de l'améliorer.... Les performances des fonds possèdent
un Benchmark doivent donc se mesure par rapport à celles de leurs
Benchmark et non dans l'absolu. «pp 165.
II.2.1.2 Probabilité d'une rentabilité
négative
C'est une généralisation de Semi - Variance,
elle consiste à calculer le pourcentage des taux de rentabilité
négatif pour un horizon de temps T spécifique de chaque titre
choisissant par l'actionnaire. Elle est définie comme suite :
T
i = 1
Avec pn,i est le pourcentage de taux de
rentabilité de iéme titre négatif.
L'inconvénient de cette mesure est qu'elle
néglige totalement les taux de rentabilité positif, de plus elle
ne tient pas compte des interrelations entre les taux de rendement des titres
considérés.
II.2.1.3 Le Downside Risk.
Afin de minimiser le risque, un investisseur, fixe souvent un
seuil minimal de taux de rentabilité qu'il ne faut pas dépasser
lors de sélection des actifs financiers. Pour cette raison, chaque fois
il doit calculer la probabilité d'avoir un taux inférieur
à un niveau fixé. Cet probabilité est appelé
Downside Risk, noté DN et donné par :
T
DN p R s i (30)
= ( )
,
Où p(Rs,i) est la probabilité d'avoir un
taux de rendement inférieur à une seuil donnée.
L'inconvénient de cette mesure est qu'elle néglige totalement les
taux de rentabilité supérieur au seuil fixé par
l'investisseur.
II.2.2 Mesure de dispersion
Les mesures de dispersion sont des mesures d'incertitude.
Néanmoins, cette incertitude ne mesure pas nécessairement le
risque contrairement aux mesures de Downsides. En effet, elles utilisent des
déviations positives et négatives au même temps et imposent
que ces déviations soient identiquement distribuées.
II.2.2.1 Mesure historiques de risque : La
variance
Le taux de rentabilité moyen est insuffisant pour
évaluer et mesurer la performance d'un actif financier pour un horizon
de temps donné. Il est plus favorable de tenir compte de la distribution
de taux de rentabilité autours de son moyen. Généralement,
on utilise la variance
des taux de rentabilité pour mesurer l'amplitude des
variations de ce dernier autour de sa moyenne.
À cet effet, on définie la variance de taux de
rentabilité d'un actif financier i et on la note
2
parói , la moyenne arithmétique des
carrés de la différence entre le taux de rentabilité et le
taux de rentabilité moyen pour une période T;
T
2 2
1 i
ó i R i t R
= ( )
- (31)
,
T t = 1
L'inconvénient de cette mesure est qu'elle s'infliance par
les taux de rendement élevés et faibles.
II.2.2.2 La volatilité
La volatilité d'un actif financier, noté
parói, est définie comme étant la
dispersion de la valeur du titre autour de sa moyenne.
ó (32)
2
= n -
1 i
n
i t i
( , )
R R
- 1
t = 1
Afin d'avoir une bonne approximation de la volatilité,
il est nécessaire de choisir un nombre d'observation très
important et d'utiliser des observations très récent (par exemple
données intraday...).
Bien qu'elle soit une mesure populaire du risque, la
volatilité ne donne pas importance à la valeur négative de
rendement, puisqu'elle traite les cours positifs et négatifs des actions
de la même façon. Un autre problème d'estimation de la
volatilité est qu'elle est instable au cours de temps : plus forte au
moment de crise et faible lorsque le marché boursier est immobile.
II.2.2.3 L'intervalle de variation
(Étendu)
Il consiste à calculer la différence entre le
taux de rentabilité le plus élevé et le taux de
rentabilité minimal de chaque titre i du portefeuille sur un horizon de
temps T. L'actif le plus risqué est celle dont son étendu est
plus élevé :
ETD= (taux de rentabilité maximal) - (taux de
rentabilité minimal) (33)
Cependant cette mesure néglige les taux de
rentabilité intermédiaire, autrement, elle ne prend pas en
considération les taux supérieurs au taux de rentabilité
minimal et inférieurs au taux de rentabilité maximal.
pi
EAM =
t =
II.2.2.4 L'écart absolu moyen
L'écart absolu moyen est la moyenne arithmétique
absolue des écarts qui existe entre le taux de rentabilité et le
taux de rentabilité moyenne, on le note par EAM et on le calcule comme
suite :
|
|
1
|
|
T
|
|
|
|
|
EAM
|
|
|
|
RitR
- i
,
|
(34)
|
|
=
|
T
|
|
|
1
|
|
|
t
|
=
|
|
|
Si les taux de rentabilité des actions, dans le
portefeuille, sont exprimés en pourcentage, autrement dit en fonction de
proportion de chaque titre, dans ce cas on utilise une autre formule pour
calculer l'écart absolu moyen :
T
(35)
RitR
- i
,
1
Où pi désigne la proportion de l'action i dans le
portefeuille.
L'inconvénient primordial de cette mesure est qu'elle
ne tient pas compte des taux de rentabilités négatifs, de plus
elle n'exprime pas le lien qui existe entre les fluctuations respectives de
taux de rentabilité entre les différents titres.
II.3 Assurance de portefeuille
A la suite de crise octobre 1987, les Risks Managers ont
recherché des nouvelles stratégies d'assurance des
portefeuilles.
La première procédure d'assurance, apparue au
début de vingtième siècle, est appelée
assurance Hedgers de portefeuille (1). A priori,
cette méthode a été rejetée par la plupart des
investisseurs parce qu'elle a crée une déviation importante au
prix des actions.
Plusieurs financiers ont tenté de construire des
modèles permettant la protection des portefeuilles contre les variations
brusques des cours d'actifs financiers, parmi ces financiers, on trouve Roy
(1952) qui a évoqué l'approche « Safety-First » dans
lequel un investisseur garantit qu'un certain montant du principal avant le
choix de portefeuille.
(1) L'assurance Hedgers de portefeuille est
une méthode d'assurance basé sur les prix historiques des titres
et le graphique d'évaluation des cours, elle consiste à vendre
les titres suite à une baisse de cours ou à acheter les actifs en
réaction à une hausse
II.3.1 L'approche Safety-First
Deux approches importantes de choix de portefeuille ont
été éditées en 1952. La première, est celle
de Markowitz qui est la théorie classique de choix de portefeuille et la
seconde, de Roy « Safety-First ». Cette dernière est la
théorie fondamentale pour le développement des mesures de risque
de chute du cours.
En effet, Roy a montré qu'un investisseur au lieu de
constituer son portefeuille en terme de fonctions d'utilité comme l'a
proposé Markowitz, il doit tout d'abord, s'assurer qu'un certain montant
du principal est préservé. Ensuite, il choisit le rendement
acceptable et minimal réalisant cette garantie obligatoire.
De même, Roy a précisé qu'un investisseur
préfère l'investissement intéressant avec la plus petite
probabilité d'investir au portefeuille plus rentable mais plus
risqué aussi.
Généralement, cet investisseur choisit ce
portefeuille en résolvant le système d'optimisation suivant ;
Min = (36)
p ( R p R 0 )
w
S/c w' I=1
avec I : vecteur unitaire.
p : est une fonction de probabilité.
Rp : taux de rentabilité du portefeuille. R0 :
niveau de rentabilité fixé.
Nonobstant, l'investisseur ne connaît pas, souvent, la
véritable fonction de probabilité. Pour cela, on fait recours
à l'inégalité des Tchebycheff (1) :
ó 2
p
) =
0
p R R
( =
p
( )
2
(37)
u R
-
p 0
Avec u p et ó p sont respectivement
l'espérance et l'écart type de portefeuille.
(1) Pour une série de variable
aléatoire x où son espérance égale à u et sa
variance égale à 2
ó i l'inégalité de
Tchebycheff
2
ó x
affirme que pour tout nombre positif c, on a
l'inégalité suivante p x u c
( )
- > =Dans notre cas
c 2
2
ó
p
0 ) 2
p R R 0 p u R u R 0
( ) ( )
p = = p - p = p -=
(u
p R - Connaissant la fonction de probabilité,
l'investisseur résout l'approximation comme suite :
S/c w'I=1
Si l'investisseur fixe un niveau de rendement R0 identique
à l'actif sans risque, ce problème d'optimisation est
équivalent à maximiser un portefeuille de ratio de Sharpe.
II.4 Mesure de risque de perte
Divers facteurs contribuent à l'apparition d'une
nouvelle mesure globale de risque, plus efficace, plus pertinent et surtout une
mesure dont tout investisseur a besoin d'en mettre confiance. Parmi ces
facteurs, on cite :
* La crise du dollar et premier choc pétrolier en 1973
* La krach de Wall-Street en octobre 1987
* La crise des monnaies européenne en 1992
* La faillite de la banque Barings en 1994
* La crise des pays asiatiques en 1997
Ainsi qu'un portefeuille diversifié reste
dépoitraillé en matière d'analyse du son risque ou encore
de le calibrer, surtout lorsqu'il renferme certains produits spécifiques
tels que les options, les devises, les obligations.
La succession de ces différentes crises a
renforcé les institutions financières à réviser
leur système de l'analyse du risque d'une part, et d'autre part de
moderniser leurs tactiques de faire face aux risques dans le but d'avoir qu'une
mesure de risque ne soit ni surestimé le risque ni le
sous-estimé.
Or puisque les mesures de risque simples sont insuffisantes
à estimer les risques des événements extrêmes, des
récentes mesures de perte sont mises en place tels que La Value-atRisk
(VaR) et l'Expected Shortfall (ES).
II.4.1 La Value at Risk (VaR)
La Value at Risk est une méthode d'évaluation des
risques fines, elle permet de quantifier les différentes nature du
risques en un seul chiffre appelé montant à risque.
D'une manière éclatante, la VaR peut être
définie comme étend la perte potentielle maximale d'un
investisseur sur la valeur d'un ou d'actifs financiers dont le rendement suit
une loi spécifiée en tenant compte d'un horizon de
détention et d'un intervalle de confiance bien
spécifié.
A partir du chiffre monétaire donné par la VaR, on
peut certifier sur le niveau du risque en fonction de la valeur du portefeuille
et de l'aversion au risque.
Selon Esch, Kieffer « la VaR d'un portefeuille ou
d'un actif pour une durée T et un niveau de probabilité
á, se définit comme le montant de perte attendu de
façon que ce montant, pendant la période [0, T], ne devrait pas
être plus important que la VaR et ceci avec une probabilité (1-
á) ».
On rappel que la VaR se focalise sur des observations
centrales, mais également elle reflète toute l'information
contenue dans la queue gauche adjoint aux pertes de la distribution des taux de
rendements d'un portefeuille d'actifs financiers. Mathématiquement on
définie la Value at Risk comme suit :
VaR (á) = F
-1(á) (39)
avec F (.) désigne la fonction de répartition
associé a la distribution des gains et des pertes.
VaRá (x) = inf {r \ P(x = r) =á }
(40)
Pr (r - VaR ) = Pr (r VaR ) =
= = á á (41)
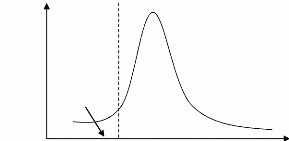
Fréquence
Probabilité
des
événements
extrêmes
VaR
Figure 8 : Distribution des profits et des pertes d'un
portefeuille
Esch, Kieffer, , "Value at Risk - Vers un Risk Management
moderne", De Boeck université 1997.
Si on admet une VaR d'un portefeuille de 10 millions sur un
niveau de confiance de 95%. Ceci implique sous les conditions normales du
marché on a seulement 5% de chance pour que la perte soit
supérieure à 10 millions.
Cependant la VaR était qualifié comme un
standard en mesure du risque, pourtant il faut l'interpréter comme
étend un instrument de contrôle et de gestion ainsi qu'un signe
d'une bonne maîtrise des risques. En effet, la VaR est un outil
adhérent dans l'identification des sources du risque dans un
portefeuille globale.
II.4.1.1 Paramètres
Comme pour toute mesure de risque, avant d'accéder aux
méthodes de calcul, il faut bien définir quelques
éléments fondamentaux dans l'interprétation d'un chiffre
VaR.
Horizon: C'est la période de
détention du l'actif ou du portefeuille, il doit être le plus
proche possible de la réalité.
La littérature a montré un horizon bref est
préférable qu'un horizon long pour deux raisons, la
première c'est que la combinaison dans un portefeuille reste stable
durant cette période, et la second est que la rareté des
donnés disponible ne pose aucune difficulté sur la
détermination de la VaR donc pour un long horizon les pertes peuvent
être graves.
Il est autorisé d'effectuer une transformation
d'horizon.
Seuil de confiance: Il indique le degré
de couverture contre le risque, ainsi qu'il reflète le degré
d'aversion des investisseurs face au risque de perte. C'est la
probabilité pour que les pertes éventuelles d'un portefeuille ne
dépassent pas la VaR donc elle doive être située entre 0 et
1 pour être significative.
Distribution des profits et des pertes du portefeuille
visés en fin du période: Valeur en fin du période
du portefeuille déduite à partir des cours historiques des titres
dans un portefeuille, c'est donc une identification du niveau d'exposition du
portefeuille en actif risqué.
Bien qu'on arrive à concevoir les caractéristiques
du VaR, pourtant que son calcul nécessite certaines simplifications.
II.4.1.2 Méthodes de calcul du VaR
Afin d'estimer la VaR, il existe une liste de modèles.
Chaque modèle a ses propres prétentions. Mais la
prétention la plus commune qui rassemble ces modèles c'est
l'exploitation des données historiques du marché pour estimer les
changements futurs.
Il est intéressant de signaler que la mise en place
d'une telle méthode dépend essentiellement des titres
étudiés, pourtant dans un univers gaussien les différentes
méthodes convergent vers des résultats très proches.
II.4.1.2.1 La méthode historique ou non
paramétrique
« Le future est le prolongement du passé »
C'est sur cette hypothèse sous-jacente qu'on part l'identification de
cette méthode. En effet, elle est fondée sur un Record des
distributions passées des rendements des actifs, et a partir des quels
on reproduit une nouvelle distribution sous l'hypothèse que ces
rendements soient iid.
Le calcule de la VaR par une telle méthode se
déroule comme suit : Il faut tout d'abord déterminer la valeur
actuelle du portefeuille. Puis, identifier les N variations potentielles toute
en classant ces valeurs historiques par ordre croissant. Finalement, en
déterminant le quantile correspond au niveau de couverture, on
déduit la VaR.
Bien que cette méthode soit la plus simple puisqu'elle
n'impose aucune hypothèse sur la nature de distribution des rendements
ou des facteurs de risque donc elle puisse être utilisée pour des
portefeuilles contenant des options.
La rareté des donnés et des nombreux calculs
peuvent apporter des problèmes quant à l'application de cette
méthode, donc on déduit que la longueur de la série affect
la qualité des résultats. Ainsi la méthode historique
suppose que le marché est stationnaire
II.4.1.2.2 La méthode paramétrique ou
analytique
Afin d'estimer la matrice du
òVariance-Covariance des rendements du portefeuille pour le
calcul de la VaR, cette méthode convoque deux hypothèses, la
première est que les taux de rentabilité suivent une distribution
gaussienne et la seconde est qu'il existe une relation linéaire entre la
valeur du portefeuille et les facteurs de risque,
Pourtant, le recours à cette approche impose certes une
faible probabilité pour les événements extrêmes.
L'application de cette méthode se déploie en trois étapes
: dans un premier temps, il faut estimer la matrice du Variance-Covariance.
Ensuite, on détermine la variance de perte du portefeuille. Enfin, on
calcule la VaR en multipliant la volatilité du ce portefeuille par le
nombre d'Êcart-type associé à un niveau de confiance
donné.
C'est une méthode rapides et simple car elle suppose la
linéarité des facteurs, ce qui écarte les
difficultés pratiques et rend l'agrégation possible mais aussi
assure une perfection quant à la précision de la VaR.
Cependant, cette méthode suppose que la matrice du
Variance-Covariance est stable c'est à dire la composition de
portefeuille et les corrélations entre ces titres sont invariables
durant la période considérée, or dans la pratique la
volatilité influent positivement les corrélations entre les
actifs financiers.
II.4.1.2.3 La méthode de Monte-Carlo
C'est une méthode sophistiquée qui consiste
à effectuer une séquence de simulation dite aussi
réévaluation sur les comportements futurs possibles des facteurs
de risque. La méthode de Monte Carlo combine deux types d'estimation,
l'une des paramètres comme pour la méthode paramétrique et
l'autre d'estimer le quantile comme pour la méthode historique.
Tant que cette procédée peut être
appliqué quelque soit la distribution des facteurs de risque sur le plan
théorique, alors que sur le plan pragmatique cette approche appelle
l'hypothèse que les prix de marché sont distribués selon
une loi gaussienne.
Cette méthode se déroule comme suit : tout d'abord,
on effectue une simulation des trajectoires d'estimation des sources de risque.
Á partir de ces facteurs simulés, on détermine la valeur
du portefeuille. On calcule, finalement, la VaR correspondante.
Cette méthode accepte tous distribution des rendements
ce qui offre une flexibilité attirante dans la mesure ou elle autorise
la modification des modèles. De plus, cette méthode tient en
considération des portefeuilles contenant des produits
dérivés.
Nonobstant, puisque la méthode de Monte-Carlo est
basée sur des processus stochastiques, son application est assez
complexe et également coûteux en matière de temps de
calcul. Autant cette approche suppose une évolution nulle du risque dans
le temps.
II.4.1.3 Limites de la VaR
Malheureusement, la VaR n'est pas la panacée des
méthodologies de mesure de risque. Cependant, le choix du
Valeur-à-Risque comme mesure de risque a été
critiqué par plusieurs théoriciens tels que Szergö (1999),
Danielsson et al. (2001) pour plusieurs raisons : dans un premier temps la VaR
n'est pas une mesure cohérente au sens d'Artzner et al. (1997). Cette
insuffisance mène à plusieurs problèmes théoriques
et pratiques. En effet, pour des distributions non normales, la VaR n'est pas
sous-additive (Embrechts et al. 2002), et peut
mener aux politiques inefficaces de diversification de risque
et aux problèmes graves dans l'exécution pratique des algorithmes
d'optimisation de portefeuille (M. Chabaane et al 2002), autrement dit si on
introduit une action additionnelle dans la composition du portefeuille, le
risque augmente donc la diversification ne permet pas de réduire le
risque total, ce qui ne reflète pas la réalité.
Tandis que son calcul pour un portefeuille donné
indique que son rendement sera au- dessous de la VaR avec la probabilité
(1- á) × 100%, elle ne fournit aucune information sur
l'ampleur de la queue de la distribution ce qui peut
être tout à fait long; dans ces cas, le rendement du portefeuille
peut prendre sensiblement des valeurs inférieures que la VaR et avoir
comme conséquences des pertes graves.
De plus, la base des donnés historiques disponibles sur
le marché, le nombre des facteurs de risque pris en considération
lors de calcul ainsi que la taille de portefeuille posent des contraintes sur
l'application et la précision de la VaR .
Pour remédier ces défauts, On a proposé
l'alternative en termes de VaR Conditionnelle ou Expected Shortfall (Artzner et
al 1997, Acerbi et Tasche 2002, par exemple), qui apprécie la
propriété de la sous-additivité.
II.4.2 La CVaR: Expected Shortfall (ES)
Néanmoins que la VaR représente une mesure plus
générale et utilisée par les plus parts des investisseurs,
des banquiers et des teneurs de marché financier, elle a
été critiqué en tant qu'étant théoriquement
délicat, puisqu'elle ne vérifie pas la sous-additivité de
théorie d'Artezner et al, et numériquement sophistiqué,
à cause de la non convexité. De ce fait une autre mesure de
risque de perte a été introduite à la fin de
vingtième siècle qui est l'Expected Shortfall.
Dans la littérature, cette mesure de risque notée
également sous le nom du Conditional Value-at-Risk et Expected tail loss
(ETL).
En effet, l'Expected Shortfall est une mesure de risque plus
pertinente et aussi puissante que la Value-at-Risk puisqu'elle tient compte des
catastrophes des événements de grands dommages encourus.
Autrement dit, la CVaR, de plus qu'elle est une mesure de perte comme la VaR,
elle est aussi une mesure des événements rare.
A cet instar, on peut définir la CVaR comme le quantile
correspondant à la perte potentielle qui peut subir un titre ou un
portefeuille suite à des mouvements défavorables des prix de
marché avec un seuil de confiance á donné sachant que
cette perte dépasse au moins
la VaR. Donc elle permet de répondre à la
question suivante : combien un investisseur peut il perdre sur un portefeuille
sélectionné avec une probabilité á et pour un
horizon de temps donnée sachant que cette perte dépasse au moins
la VaR ?
Par conséquence, la CVaR est une mesure relative de
risque, elle est définie comme étant l'espérance
conditionnelle des pertes dépassant la VaR pour un niveau de confiance
donné. Pour un portefeuille, elle est équivalente à
l'espérance conditionnelle des rendements des titres au-dessous du
rendement de la VaR.
Comme présenté par Rockafellar et Uryasev (2000),
pour des distributions continues, CVaRá d'un titre p et de
taux de rendement égale à Rp est donnée par :
CVaR R E R R VaR R
á = - - = á
( ) ( / ( )) (42)
p p p p
En outre la VaR est le minimum de l'équation (16) pour
cela elle peut être une solution optimale de cette fonction et dans ce
cas la CVaR est égale à la VaR.
Une autre définition peut être
élaborée à l'Expected Shortfall est l'addition d'une Mean
Exess (moyenne de perte) à la VaR. En effet, la figure (9) montre que la
CVaR á d'un
portefeuille est plus élevée que la VaR
á. De ce fait, la VaR-conditionnelle est
donnée par l'équation suivante :
CVaR ( R p ) = VaR +
Moyenne de perte dépassant la VaR (43)
á á á
CVaR (R p ) = VaR + VaR
-
á á å ( á ì)
(44)
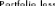
Figure 9 (1) : VaRá et
CVaRá d'un portefeuille
(1) On extrait cette figure de l'article «
VaR, CVaR and mean-downside Risk portfolio selection » des auteurs Paolo
Vanini et Luigi Vignola page 5.
Rockafellar et Uryasev (2002) ont montré que la CVaR
est une mesure cohérente de risque au sens d'Artezner et al et ils ont
exposé la justification dans leur article «Conditional
value-at-risk for general loss distributions«. De plus ils ont
dévoilé que cette mesure peut être estimée
même dans le cas où l'estimation de la VaR est
échouée.
D'autre part, pour des répartitions discrètes,
la formule (42) conduit à une fonction non convexe en position de
portefeuille, et aussi à une mesure non sous-additive de risque. Une
définition de CVaR pour des distributions générales
(répartitions discrètes y comprîmes) a été
présenté par Rockafellar et Uryasev:
1 1
CVaR ( 1
= - p) Z + p R (45)
á s s s
1 - á { } { }
1 - á
s / R Z
? Ù = s / R Z
? Ù =
s s
T
Avec Ps : la probabilité positive
associée au titre s tel que ps = 1 et Z =
VaR á
s = 1
Pflug (2000) a montré que l'Expected Shortfall est plus
significatif que la Value-at-Risk, particulièrement, quand les
données du marché suivent une distribution discrète et/ou
non normale.
En discutant quelques propriétés
mathématiques de la CVaR, elle est toujours plus petite ou bien
égale à la VaR. mais comme nous avons mentionné ci-dessus,
CVaR est une mesure cohérente tandis que le VaR ne l'est pas. On peut
également montrer que ES est une fonction concave
(1) et a, en conséquence, un minimum unique.
II.5 Comparaison entre la volatilité, VaR et
CVaR
Pendant longtemps, la volatilité était la mesure
des risques financiers la plus dominante, grâce à sa
simplicité. D'autre part, la VaR est imposée par les
régulateurs comme mesure plus pertinente, alors que la CVaR est
recommandé par plusieurs statisticiens comme mesure alternative au VaR.
A cet instar, le tableau (1) résume les caractéristiques
particulières de chaque mesure.
(1) La démonstration de convexité
de CVaR á a été élaborer par
Paolo Vanini et Luigi Vignola dans l'article «VaR, CVaR and mean-downside
Risk portfolio selection«
Tableau 1 : Comparaison entre la Volatilité, la
VaR et la CVaR.
|
Volatilité
|
|
La VaR
|
|
La CVaR
|
|
-Représentation commode et simple des risques (un seul
nombre)
- Mesure standard de risque et utilisé par les plus part
des investisseurs.
- Cohérente au sens d'Artzner et al.
- S'infliance par les rendements élevés et
faibles.
- Inapplicable aux distributions non linéaires, tels que
des options, avec des distributions non normales.
-On peut appliquer une procédure de validation de la
volatilité telle que test d'homoscédasticité et
d'autocorrélation.
|
|
-Représentation commode et simple des risques de perte (un
seul nombre)
- Mesure standard de risque de perte et utilisé par les
plus part des investisseurs
- Non cohérente au sens d'Artzner et al car elle ne
vérifie pas l'axiome de sousadditivité.
-Une mesure de risque de chute du cours.
- Applicable aux distributions non linéaires.
-On peut appliquer une procédure de validation de la VaR
tel que Backtesting
-Ne mesure pas des pertes dépassant la VaR.
|
|
- Représentation commode et simple des risques de perte
(un seul nombre)
-Mesure recommandé pour des pertes excédant la
VaR.
- Cohérente au sens d'Artzner et al.
-La meuilleure mesure de risque de chute du cours
-Applicable aux distributions non linéaires.
-Pas facilement d'appliquer les méthodes Backtesting
pour tester la validation de CVaR
-Plus conservatrice que la VaR: elle mesure les risques au
delà de la VaR.
|
| 


