I.5 Risque systématique
On rappel que le risque globale dans un portefeuille
composé d'actifs financiers, rejoint deux types de risques qui sont le
risque spécifique et le risque systématique liés aux
fluctuations des facteurs du marché.
En effet, le risque systématique en tant que la seule
source d'incertitude dans un portefeuille efficient résulte de la
corrélation entre la rentabilité des portefeuilles efficients
avec celle du portefeuille de marché. L'expression du risque
spécifique est donné par :
N
1
ó 2 ó
=
N 1
i=
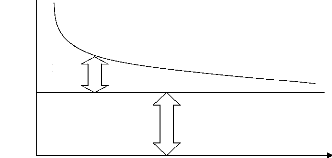
Il convient de noter qu'il existe une relation entre le risque et
le nombre des titres dans un portefeuille, à ce cotexte on avance le
schéma suivant :

5 10 20 50
óPF
R. div
R. systématique
Limite: COV
Nombre de titres
Figure (5) : L'effet de diversification sur le risque
d'un portefeuille
On observe que la réduction du risque est d'abord
très rapide, toutefois elle se freine assez vite. Ceci est due au faite
que le risque systématique est non éliminable par diversification
en raison d'effet de covariance des plus parts des titres.
Markowitz note que « le risque d'un portefeuille bien
diversifié tend vers la moyenne des
covariances des titres inclus dans le portefeuille
» C'est-à-dire ; si N ? 8 ,
ó2PF ?
COV
Il faut mentionner que le risque systématique,
mesuré par Bêta, ignore les risques diversifiables, les risques
asymétries ainsi que les risques spécifiques à chaque
institution financière.
I.6 Le modèle de Markowitz et
détermination de frontière efficiente
Markowitz affirme dans sa théorie que la moyenne et la
variance des taux de rentabilité sont les critères les plus
pertinents en matière d'évaluation des actifs.
Pour analyser cette approche, cette section, souligne la
technique du choix des portefeuilles.
I.6.1 Calcul des portefeuilles efficients
Il est très connu que tous les investisseurs
préfèrent une espérance de rentabilité
élevée ainsi qu'une variance faible. Toute fois, pour un niveau
de risque, on préfère une rentabilité élevée
à une autre moins élevée. Pour se faire, il est judicieux
de rappeler que les courbes d'indifférence représentent la mesure
la plus efficace des préférences des investisseurs,
c'està-dire déterminer le degré de risque qu'un individu
est prêt a accepter afin d'obtenir un certain taux de rentabilité
aléatoire.
Il est maintenant possible de choisir le meilleur portefeuille
dit portefeuille optimal qui correspond à la meilleur combinaison entre
le rendement et le risque en appliquant les concepts de probabilité.
A ce niveau là, Markowitz intervient, une fois encore,
en introduisant la notion du portefeuille dominant, connu encore sous le non du
portefeuille efficient, qui consiste à déterminer le taux de
rentabilité espère le plus élevé pour un niveau de
risque fixé.
A ce propos, Markowitz admet comme cible la détermination
des portefeuilles efficients en les traçant sur un plan (rendement
espéré, risque).

Frontière efficiente
Ensemble des couples (moyenne variance)
*
* *
**
* * * * * * * * * * * * * *
* * ** **
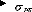
Courbes d'indifférences

EPF
Figure (6) : Le choix du portefeuille
efficient
D'après le graphique, on observe que pour chaque niveau
de risque, il existe un portefeuille qui maximise le rendement attendu ou
encore, pour chaque niveau de rendement, il existe un portefeuille qui minimise
le rendement. L'ensemble de ses portefeuilles construit la frontière
efficiente de Markowitz.
On remarque que par construction, la frontière est convexe
ce qui provoque que le risque n'augmente pas linéairement en fonction
des poids d'actifs dans le portefeuille.
Il est à noter que la région située au
dessus de la frontière implique qu'un tel portefeuille est impossible
à construire, alors que région située au dessous de la
frontière implique que ces portefeuilles sont sous-optimaux et
n'intéresseront pas un investisseur rationnel.
Le problème ici se manifeste par la
détermination du portefeuille optimal, en d'autre terme celui qui
coïncide avec la courbe d'indifférence. Pour se faire, le
problème se résoudre par une simple translation de la courbe
d'indifférence jusqu'au atteindre une tangente entre cette
dernière courbe et celle de la frontière efficiente, bien que
cette tangence représente un portefeuille efficient.
D'une manière plus précise, le portefeuille
optimal est celui qui correspond, pour un investisseur, le mieux aux
caractéristiques de sa fonction d'utilité particulière
c'est à dire en fonction de ces préférences en
matière de rendement ainsi que du risque.
Mais comment bâtir un tel portefeuille ? La réponse
fait l'objet de la suite.
En fait, le but de cette partie c'est de trouver les proportions
Xi à investir dans les différents titres à travers la
résolution de ce système.
Min X X X (18)
i j ij
ó
N
i = 1 N
1
Xi
i = 1
avec Ei : Rendement espéré du titre.
Xi : Proportion investie dans le titre i.
óij : Covariance des rendements des titres i et
j.
óii : Variance des rendements du titre i.
On fera appel à la méthode des multiplicateurs de
Lagrange qui consiste à minimiser
*
|
l'expression de Lagrange, pour chaque niveau de E
|
, qui est donner par :
|
|
N
|
N
|
N
|
N
|
|
Z = X i X j ó ij
|
+ ë ( E*)
Xi E i ë2
- +
1
|
( 1) (19)
Xi -
|
|
i
|
= 1 1
j =
|
i
|
=1
|
i
|
=
|
1
|
Résoudrons cette équation :
?X1
?Z = 2X1 ó11 +
2X2ó12 + .+
2XNó1N + ë 1 E1 +
ë2 = 0 (20)
.
.
?XN
?Z = 2 X1 óN1 +
2X2 óN2 + + 2 XNó
NN + ë 1 EN +
ë2 = 0 (21)
?Z
?ë1
?Z
?ë2
= X1E1 + X2E2 + +XNEN - E* = 0
(22)
= X1+ X2 + XN -1 = 0 (23)
On obtient un ensemble de (N+2) inconnus qui peuvent
s'écrire sous la forme matricielle : C.X= K (24)
|
2 2
ó ó
11
|
121 1
. . 2 1
ó E N
|
X 1
|
0
|
|
:
|
:
|
:
|
:
|
:
|
:
|
:
|
:
|
|
avec C=
|
2 2 . . 2 1
ó ó ó
N N NN N
E
1 2
|
,
|
X= XN
|
et K =
|
0
|
|
E1
|
E E
..
2 N
|
00
|
ë 1
|
E
|
*
|
|
1 1
|
..
|
1 00
|
ë2
|
1
|
Par un simple jeu mathématique, on arrive à trouver
que X = C-1 .K
Le vecteur X représente la structure du portefeuille
efficient pour le niveau de rendement
|
espéré E*
|
. On enregistre finalement une série des portefeuilles
efficients correspond chacun
|
par un niveau de rendement espéré donné.
L'ensemble de ces portefeuilles efficients constitue la frontière
efficiente.
Black (1972 P.448-449) a bien démontré que la
combinaison de deux portefeuilles efficients est un portefeuille efficient,
donc il légitime de conclure que toute combinaison linéaire de
deux portefeuilles est un portefeuille efficient.
I.6.2 L'introduction d'un actif sans risque
Jusqu'à présent, nous avons analysé des
portefeuilles composés d'actifs de nature risqués. Toute fois,
sur le marché réel il existe des actifs sans risque, et
l'introduction d'un tel actif permet à l'investisseur de prêter et
d'emprunter au même taux.
Puisqu'il ne soutient aucun risque, un actif sans risque est
caractérisé par un taux de rémunération
parfaitement certain, une variance nulle ainsi qu'une covariance nulle avec les
autres actifs risqués. Il est généralement associé
aux titres émis par l'Etat à court terme sous forme de Bon de
Trésor, donc son rendement est connu à l'avance.
De ce faite, on note que l'introduction d'un actif sans risque
n'a aucun effet sur l'expression de la variance des portefeuilles cependant, il
apportera des modifications sur ces deux contraintes.
N
(25)
* *
Xi Ri + X + R
= E
N 1 F
i 1
=
N 1
+
* X i 1 (26)
=
i 1
=
En effet, l'espérance de rentabilité est
formée de l'actif sans risque augmenté d'une prime de risque et
l'expression de Lagrangien devient :
|
N
|
N
|
N
|
N+
|
1
|
|
Z = X i X j ij
ó +
|
ë ( N F
X i E i X 1
R
+ +
1
|
- E*) + ë2 (
|
Xi -1) (27)
|
|
i 1 1
= =
j
|
i=1
|
i
|
=
|
1
|
Suivant une même démarche de résolution, on
déduit le vecteur Xi.
De ce fait, on déduit que le rendement
espéré de ce portefeuille est exprimé par une droite
quelque soit la proportion investie dans l'actif sans risque.
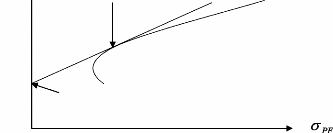
RF
A
Figure (7) : Frontière efficiente avec un actif
sans risque
On constate que l'introduction d'un actif sans risque
transforme la frontière efficiente en une droite partant par le niveau
de l'actif sans risque RF, de façon de toucher la pente la
plus élevé autrement dit la pente de la tangente avec la
frontière définie par Markowitz et cette droite représente
l'ensemble des combinaisons possibles entre l'actif sans risque et l'actif
risqué, autrement, elle offre de nouvelles opportunité
d'investissements donc augmenter son niveau de satisfaction. Cette droite est
connue sous le nom CML(1) « Capital Market
Line ».
Bref, un investisseur opte pour un portefeuille situé
sur le point A, déplie tout ses richesses dans l'actif sans risque.
Cependant, dans le point B l'investisseur place tout son argent dans l'actif
risqué. Un point situé entre A et B implique qu'un tel
investisseur reparti son capital entre l'actif sans risque et l'actif
risqué.
On peut déduire finalement que selon cette approche,
l'optimisation de portefeuille est faite en deux étapes ; la
première était de trouver la combinaison optimale des actifs
risqués en identifiant les poids optimaux pour chacun des titres
composant un portefeuille et la deuxième c'est d'ajouter à ce
portefeuille optimal une certaine proportion d'actif sans risque.
I.6.3 Théorème de
séparation
Dans ce contexte, il intervient à notre esprit une
question fondamentale qui est la suivante : Existe-il une relation entre
l'attitude de l'investisseur en face au risque d'une part, et d'autre part le
choix des combinaisons d'actif risqué ?
(1) on rappel que la droite du marché CML
exprime que le rendement espéré du portefeuille est égal
au taux sans risque plus une prime du risque spécifique à ce
portefeuille.
Markowitz a été principalement
intéressé par la diversification des titres risqués. Tobin
(1958) a ajouté le concept de combiner les actifs sans risque avec les
titres risqués lors de choix du portefeuille. Dans la même logique
de l'approche classique Moyenne-Variance on définie la
théorème de séparation comme suite ; la sélection
de portefeuille optimal pour un niveau donné de tolérance de
risque peut être séparé en deux étapes: d'abord
trouvant un mélange optimal des titres du marché invariant avec
le risque, et ensuite le combinant avec une quantité appropriée
d'actifs certains. C'est-à-dire, il y a une séparation entre les
choix des actifs risqués qui sont le même pour tous les
investisseurs et l'ajout des titres sans risques qui dépendent de
degré d'aversion au risque.
En effet, cette théorie évoque que la
sélection des proportions des actifs risqués des portefeuilles ne
dépend pas de degré d'aversion au risque de l'investisseur. Par
contre la répartition de sa richesse entre les actifs risqués et
les titres certains est basée sur son aversion au risque. Par
conséquent, le choix de portefeuille est fondé sur les
capacités de l'agent d'investir dans le marché financier et ne
plus de l'aversion au risque même dans le cas où il n'y a pas des
actifs certains.
I.6.4 Limites du modèle classique
Comme pour tout modèle, les limites sont
généralement focalisées autours de ces hypothèses
ainsi que sur l'estimation de ces paramètres.
En effet, en cas de défaut, ou encore en cas des pertes
exceptionnelles l'hypothèse de normalité n'est plus vigoureuse
à cause d'une part, l'excès de probabilité des
événements aérogares, et d'autre part l'asymétrie
des rendements c'est à dire que cette approche ne différencie pas
les variations positives (ampleur des variations au-dessous de la moyenne)
à celle négative (ampleur des variations au dessous de la
moyenne).
En outre, le modèle moyenne variance suppose que les
premiers moments sont explicitement suffisants afin de condenser toute
l'information englobée au tour des séries des rendements des
actifs financiers.
De plus, les indicateurs traditionnels préjugent que
les facteurs de marché reste sédentaire pendant la durée
d'investissement ce qui est loin d'être réelle. Par analogie,
l'approche traditionnelle suppose que la volatilité est durable dans le
temps nonobstant, dans la pratique, plusieurs facteurs associés à
la volatilité évoluent au cours de temps tel que le taux
d'intérêt, le bénéfice, les facteurs
macroéconomiques ainsi que l'importance du l'allocation des fonds.
La volatilité n'est plus valides en cas des
portefeuilles complexes c'est-à-dire ceux qui contiennent les produits
dérivés et souvent incapable d'estimer avec précision les
risques et surtout extrêmes.
Tous ces limites nous font douter sur la pertinence des
résultats quelles nos procurent.
| 


