Gestion de Portefeuille Obligataire : Cas de la Banque Nationale d'Algérie (BNA)

Section 2. L'évaluation des obligations

La théorie de taux d'intérêt a toujours été considérée comme un élément fondamental dans les choix financiers, celle-ci s'avère incontournable en gestion financière. A cet effet, les variations des taux d'intérêt prennent autant d'ampleur qu'elles peuvent affecter les choix d'investissement.

Nous avons vu dans la première section de ce chapitre que les outils actuariels étaient des instruments fiables d'analyse du risque de taux, ils s'avèrent contraignants pour les investisseurs d'autant qu'ils considèrent la constance des taux de rendement sur la période d'emprunt.

Ainsi, il s'agira dans cette section, d'explorer les facteurs qui régissent le niveau de taux d'intérêt et déterminant les prix des obligations.

1. Le taux d'intérêt

« Le taux d'intérêt est le prix du service immédiat de liquidité pendant une certaine période. Il est associé à un contrat par lequel le prêteur met à la disposition de l'emprunteur des liquidités. L'intérêt ici est le revenu certain qui découle de l'immobilisation des ressources monétaires pendant une certaine durée. Il s'agit de la rémunération du service de la liquidité dans la durée »¹.

En effet, le contrat obligataire oblige le prêteur à sacrifier une somme actuelle au profit de l'emprunteur, rémunérant un intérêt basé sur un taux établit en pourcentage sur cette somme, augmenté à la fin de la période du montant de la transaction. Par exemple, un prêteur donne 100.000 DA à un emprunteur pour la durée de 1 an au taux R, il a sacrifié de la liquidité immédiate en vue de revenus futurs. Il recevra 10.000 DA d'intérêts dans une année augmentés de la somme payée en début de période. Il aura dans une année : 100.000* (1+R) = 110.000.

Ce qui nous donne un taux d'intérêt de : R = 110.000

100.000 - 1 = 10%.

Le taux d'intérêt permet d'établir une relation entre la valeur d'un investissement immédiat et les paiements futurs liés à cet investissement.

2. L'évaluation des obligations 2.1. Valeur d'une obligation

Nous savons que la valeur monétaire d'une créance est différente que l'on se situe à un
moment actuel ou futur. En effet, bien que la valeur que paye l'investisseur aujourd'hui

CHAPITRE I : Approche actuarielle et évaluation obligataire	) Le coupon couru prend la formule : 47

soit différente de la valeur des coupons et remboursements qu'il recevra dans le futur, le prix qu'il paye est lié aux sommes futures à un taux d'intérêt donné. Le principe de l'actualisation permet d'uniformiser les valeurs à une date donnée.

Le prix d'une obligation s'exprime selon la formule suivante :

P = I

n ( CFi

i=1 (1-Fr)i)

Avec P: prix théorique de l'obligation à un instant donné ; CFi : Flux monétaires (coupon + remboursements); r : taux de rendement ;

i : période d'investissement.

Cette formule permet d'obtenir le prix d'une obligation à n'importe quel moment de la période de placement. A cet effet, il s'agit simplement de prendre en considération les coupons courus jusqu'à ce moment.

Supposons que l'on se situe à M mois après le jème coupon, le prix de l'obligation sera :

_In-j

Fi

+1

( (i+

r

)

i

-

m

it

2

) P'=(2.1

i=

1

K*c*M

Coupon couru =
	1200

Où K : capital payé en début de période ;

c : taux du coupon ;

M : nombre de mois écoulés après le jème coupon.

2.2. Relation prix/taux de rendement actuariel

Le comportement financier des investisseurs sur le marché laisse entendre que les deux facteurs prix et taux actuariel de rendement sont liés mais inversement. En effet, la réalité du marché impose le fait que les investisseurs optent pour les investissements les plus rentables, par conséquent, si les taux d'intérêt subissent une hausse, l'investisseur aura intérêt à vendre son obligation afin d'investir dans d'autres, et toutes choses égales par ailleurs, on assistera à une baisse des prix des obligations. Par ailleurs, en cas de baisse des taux d'intérêt, le cours de l'obligation augmente.

Il est plus judicieux de présenter cette relation en graphique, en considérant une obligation remboursable in fine à taux de coupon de 11% et ayant une maturité de 5ans :

48

CHAPITRE I : Approche actuarielle et évaluation obligataire

Prix(%)

160

140

120

Obligation à coupon 11%, maturité 5ans

60

40

20

0

y=3% y=5% y=7% y=9% y=11%y=13%y=15%y=17%y=19%y=21%

Taux de rendement actuariel

100

80

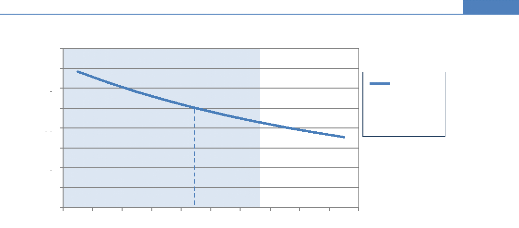
Graphique n° 3 : Relation entre le prix d'une obligation et son taux de rendement actuariel (yield).

D'après le graphique ci-dessus, nous pouvons constater que pour un taux de rendement de 11%, l'obligation vaut le pair (100%). Aussi, pour une valeur y=0%, le prix de l'obligation n'est autre que la somme des cash-flows générés par celle-ci, à savoir 155% et pour valeur infinie y = 8%, la valeur de l'obligation est nulle (P₈=0). Par conséquent, on peut déduire la relation inverse entre ces deux facteurs à travers la lecture de la forme de la courbe représentée dans le graphique.

Par ailleurs, la courbe obtenue prend une forme convexe et non linéaire, cette forme provient de l'influence d'autres paramètres à savoir la maturité de l'obligation et son taux de coupon.

2.3. Effets sur la variation des prix obligataires

Généralement, les facteurs pouvant affecter les prix des obligations sont : le taux de coupon, la maturité, leur asymétrie et leur convergence vers le pair.

2.3.1. L'effet coupon

En considérant deux obligations dont les caractéristiques sont similaires à part le taux de coupon, plus celui-ci est grand plus la variation du prix de l'obligation sera faible.

Penons un exemple pour l'illustration de ce point où on considère trois obligations aux mêmes caractéristiques sauf le taux du coupon qui diffère. Ainsi, on considère deux obligations A et B à taux respectifs de 9% et 4,5% et une obligation Z à zéro-coupons qui nous servira d'appui pour mieux interpréter les résultats.

A noter que chacune des obligations a une maturité de 6 ans et vaut le pair (100%) à une date D.

Ainsi, pour une variation à la hausse de 1% du taux de rendement actuariel (de 10% à 11%), on obtiendra les résultats qui sont représentés dans le tableau 2 et schéma 4 suivants :

Tableau n° 2: Effet du coupon sur la variation du prix de l'obligation

	Ancien prix (%)	Nouveau prix (%)	Variation relative
Taux de rendement	Y=10%	Y=11%	Ay = +1%
Obligation A (9%)	95,65	91,54	(4,29)
Obligation B (4,5%)	76 ,05	72,50	(4,66)
Obligation Z (0%)	56,45	53 ,46	(5,29)

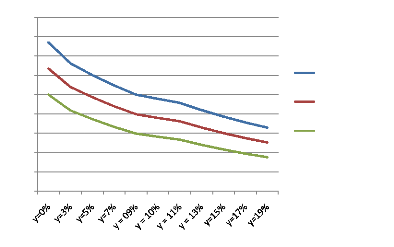
La hausse du taux de rendement de 1% a provoqué une baisse considérable des prix pour les obligations zéro-coupons. Néanmoins, l'obligation ayant un fort taux de coupon voit son prix baisser mais à des proportions moindres que la première. Ces résultats nous montrent effectivement que plus le taux de coupon est élevé le prix baisse moins. Il s'en sort que le prix du titre assorti du coupon le plus élevé est supérieur pour un taux actuariel donné.

180

160

140

120

100

80

40

60

20

Prix

0

Taux de
rendement

Obligation A (9%)

Obligation B

(4,5%)

Obligation Z (0%)

Graphique n° 4 : Illustration de l'effet coupon sur la variation des prix des obligations.

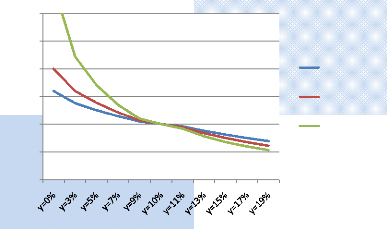
2.3.2. L'effet maturité

Dans toute situation d'équilibre, on considère que plus maturité d'une obligation est
longue, plus les fluctuations des prix sont élevés, ceci s'explique par l'évolution du taux

300

250

200

150

100

50

0

Prix

Taux de
rendement

Obligation A (6ans)

Obligation B (10ans)

Obligation C (25ans)

de rendement pendant la période. Il existe une relation croissante entre la maturité et le prix d'une obligation.

Cette relation peut être vérifiée en considérant l'exemple suivant :

Soient trois obligations (A, B, et C) cotant le pair (100%) et remboursables in fine dont le taux du coupon s'élève à 10%, ayant des maturités différentes respectivement de : 6, 10 et 25ans, les résultats de la variation des prix en prenant en compte une situation d'évolution du taux de rendement de 1% à une certaine période T, sont présentés dans le tableau 3 ci-après avec comme illustration un graphique n°5 montrant l'effet de cette hausse sur les prix de chacun des titres :

Tableau n°3: Variation des prix selon la maturité

	Ancien prix (%)	Nouveau prix (%)	Variation
Taux de rendement	Y=10%	Y=11%	Ay = +1%
Obligation A (6ans)	100	95,77	(4,23)
Obligation B (10ans)	100	94,11	(5,89)
Obligation C (25ans)	100	91,58	(8,42)

La hausse du taux de 1% a eu pour effet la diminution des prix des trois obligations ; néanmoins, cette baisse est d'autant plus grande pour l'obligation à longue maturité (25ans) dont le prix a chuté de près de 8,5% alors que celui-ci n'a baissé que de 4,23% pour l'obligation A (6ans). Ainsi, en multipliant la maturité par 4 fois et pour le même coupon, l'obligation ne vaudra que le double de sa valeur.

Enfin, ces résultats peuvent être résumés dans le graphique suivant :

2.3.3. L'asymétrie : Effet d'une variation de taux de rendement sur les prix

Toutes les obligations ne voient pas leurs prix varier avec la même amplitude pour une variation de taux identique (la simulation prise en compte est une hausse de 1%). En effet, celle résultant d'une baisse de taux est plus importante du fait de la convexité de la relation liant les prix aux taux de rendement actuariels.

Prenons l'exemple d'une obligation à taux de coupon de 9% et de maturité de 5ans et considérons les résultats présentés dans le tableau 4 ci-après pour une hausse et une baisse de 1% du taux de rendement :

Tableau n°4: Asymétrie des variations des prix des titres

Variations des taux	Ay=0%	Ay=1%	Ay=-1%
Taux de rendement	y=9%	y=10%	y=8%
Obligation 9% (5ans)	100	96,209213	103,99271
Variations des prix	0	-3,79079	3,99271

D'après ces résultats, nous pouvons constater que si le taux de rendement augmente de 1% les prix baissent, et qu'une même variation à la baisse de y engendre la hausse des prix mais avec des proportions plus grandes que dans le premier cas. L'écart entre les variations des prix est de seulement E=0,202%.

Par ailleurs, une variation Ay=#177; 5% nous donnera un écart entre les variations des prix de : E1=5,094%. Ce qui représente un écart considérable par rapport au cas de variation de #177;1%.

Enfin, l'asymétrie nous démontre bien la relation convexe existant entre le prix et le taux de rendement actuariel de l'obligation.

2.3.4. La convergence vers le pair

Les prix des obligations évoluent avec le temps et tendent de plus en plus vers le pair (ou bien vers la valeur du remboursement s'il n'est pas égal au pair) surtout à l'approche de l'échéance du titre, peu importe le niveau du taux d'intérêt.

Prenons un exemple d'une obligation à coupon 10%, maturité : 6ans, taux de rendement : 12%. Après les calculs, on obtiendra le tableau suivant :

Tableau n°5: Convergence vers le pair des prix obligataires

Durée jusqu'à l'échéance	6ans	5ans	4ans	3ans	2ans	1année
Prix pour taux de rend. : 12%	91,78	92,79	93,92	95,20	96,62	98,22
Prix pour taux de rend. : 10%	100	100	100	100	100	100
Prix pour taux de rend. : 08%	109,25	107,98	106,63	105,15	103,57	101,85

A partir des données de ce tableau, nous obtiendrons le graphe ci-après :

115

110

105

100

95

90

85

80

Prix

6ans 5ans 4ans 3ans 2ans 1année

Durée à échéance

Taux de rendement 12%

Taux de rendement 10%

Taux de rendement 08%

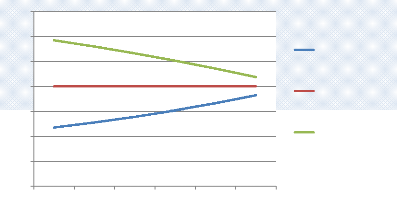
Graphique n° 6 : Convergence vers le pair obligation TC=10%, 6ans.

Comme le montre le graphique, les prix évoluent dans le temps et finissent par converger vers la valeur du pair. Cependant, le graphe montre bien que cette évolution est différente selon qu'on prenne en compte une obligation surcotée, au pair ou décotée ; l'obligation surcotée aura un prix qui diminue jusqu'à atteindre la valeur du remboursement, de son coté, l'obligation décotée verra son prix augmenter jusqu'à un certain seuil et enfin, l'obligation cotée au pair aura un prix constant jusqu'à l'échéance du titre.

Les différents concepts développés ci-dessus permettent l'estimation des variations des prix des obligations seulement pour des taux de rendement donnés. Ainsi, un autre concept vient pallier à cette insuffisance : c'est la structure par terme de taux d'intérêt (STTI) qui permet l'estimation des variations des prix de titres suite à des changements de taux de rendement.

3. La structure par terme de taux d'intérêt

La structure par terme des taux d'intérêt acquiert le statut d'objet d'analyse à part entière vers la fin des années trente, sous la direction de Hicks (1939) et Lutz (1940). La problématique concernant les taux a évolué des façons les plus remarquables pendant ces 40 dernières années, les analystes sont allés jusqu'à surnommer cette période par « l'âge d'or » des théories traditionnelles de la structure des taux.

A la fin des années 80, les nouvelles théories qui apparaissent ont eu beaucoup d'effet notamment à la dissolution des théories classiques qui, selon les analystes, contenaient des processus trompeurs à la réalité financière.

L'étude des théories de la structure par terme est assujettie à plusieurs hypothèses fondamentales qui ne sont pas toujours des plus « réalistes ». Ainsi, nous distinguons deux éléments qui expliquent ces théories. Le premier est lié aux anticipations des investisseurs qui ne s'intéressent qu'aux rendements qu'ils espèrent dégager dans le futur. De là découlent deux possibilités (toutefois présentées comme deux alternatives)¹ : soit l'investisseur connait les taux d'intérêt qui prévaudront dans le futur ou bien il est incertain de l'évolution de ceux-ci mais espère obtenir le meilleur rendement possible.

Le deuxième facteur concerne le comportement de l'investisseur envers le risque : soit il a de l'aversion au risque², soit il est neutre envers le risque ou bien il aime le risque.

Dans nos jours, la gestion obligataire repose beaucoup sur la théorie du taux d'intérêt. Celui-ci évolue constamment et régulièrement en fonction de la durée d'investissement des titres financiers. La relation qui lie le taux d'intérêt à la durée du titre est représentée par une courbe appelée « Structure par terme de taux d'intérêt ».

3.1. Définition

La structure par terme de taux d'intérêt ou courbe de taux est le terme attribué à une représentation graphique, à un moment donné, des taux de rendement sur un marché en fonction de la durée de l'investissement. On retrouve des courbes de taux en fonction de la vie moyenne, de la duration ou de la durée de vie à l'échéance.

Ces courbes peuvent être construites en référence à des emprunts à zéro-coupons, in fine ou amortissables mais dont le choix est complètement empirique. Elles reposent notamment sur des titres dont les caractéristiques sont homogènes (mode de remboursement, risque de défaut ou de liquidité... etc.).

¹ En effet, nous étudierons les anticipations dans un avenir certain et les anticipations dans un avenir incertain.

² Un investisseur qui a de l'aversion au risque signifie, toutes choses étant égales par ailleurs, qu'il préfère les distributions de probabilité de gains les moins dispersées, i.e. qu'il n'a pas de préférence pour le risque.

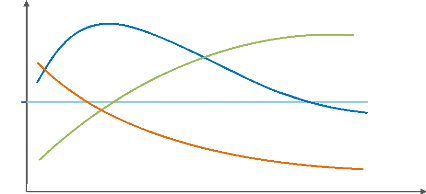
En pratique, on représente la structure de taux à un instant donné sur un graphe où l'on projette en abscisse la maturité et en ordonnée l'ensemble des taux spot : {Rt,1, Rt,2, Rt,3,..., Rt,n}. En général ¹ , elle peut être : ascendante, en cloche, horizontale ou descendante :

(2)

(1)

5%

(3)

(5)

Taux

Maturité

Graphique n° 7 : Les formes de la structure par terme de taux

> (1) : courbe ascendante : la plus fréquemment observée où les taux croissent avec l'échéance et donc les taux longs sont supérieurs aux taux courts ;

> (2) : courbe en cloche : les taux augmentent jusqu'à atteindre un maximum puis décroissent. Cette forme est plus en vue en période de hausse des taux ;

> (3) : courbe plate : forme très rarement observée sur le marché. Cette forme est expliquée par la stabilité de l'évolution future des taux d'intérêt ;

> (4) : courbe descendante : où les taux longs sont inférieurs aux taux courts. En fait, en situation de déclin économique, les investisseurs anticipent une diminution des taux à court terme et acceptent donc d'investir à long terme pour des rendements inférieurs.

Nous présenterons dans ce qui suit un modèle de structure par terme des taux en avenir certain puis incertain.

3.2. La structure de taux dans un univers certain

L'univers est dit « certain » lorsque les agents économiques ont une parfaite connaissance du futur, ce qui signifie qu'ils ont une idée précise sur les valeurs futures. Cette hypothèse est quasiment irréaliste dans un marché où les taux évoluent de façon permanente et continuelle.

Concernant la structure de taux dans un environnement d'anticipations certain, Leroy (1982) a dit que « Parce qu'en certitude, les taux de rendement sur les bons (et sur tout autre actif) sont égaux sur des intervalles comparables même lorsque les taux d'intérêt varient au cours du temps, les individus sont indifférents vis-à-vis de la maturité des bons qu'ils émettent ou détiennent. En conséquence, il n 'y a rien d'intéressant à dire à propos de la relation entre des bons de maturité différente. ».

Cependant, sachant que la plupart des théories traditionnelles se sont basées sur des hypothèses qui relèvent du monde certain, ce qui permettra de mieux comprendre le mécanisme de construction de la structure par terme.

Ce modèle, exposé autrefois par Lutz (1940), repose sur plusieurs hypothèses 3.2.1. Hypothèses

> Les titres transigés sont remboursables in fine, de maturité n, ayant un taux de

rendement _Rt,n , ?n ;

> Le marché considéré est supposé parfait : pas de coût de transaction ni coût d'information et un risque de défaut quasi nul. On dit que c'est un marché walrassien où les ventes à découvert sont admises ;

> Les agents ont des comportements rationnels et préfèrent toujours plus à moins¹ ;

> Etant dans un avenir certain, les agents économiques connaissent parfaitement les taux d'intérêt passés, présents et futurs.

Les trois premières hypothèses constituent la référence commune pour les diverses théories explicatives de la structure par terme de taux. La dernière hypothèse est propre aux caractéristiques du monde certain.

3.2.2. Stratégies d'investissement

Dans ce cas, on suppose que l'investisseur obtienne un rendement sûr pour n'importe quelle combinaison d'échéances, et comme l'avenir est plus que probable, il pourra prévoir le taux d'intérêt à une période dans le futur.

D'une manière générale, la stratégie de l'investisseur ayant des titres en t pour n périodes, impose le fait qu'il lui est équivalent dans un monde certain :

> D'investir en t dans des titres de maturité n et les conserver jusqu'à l'échéance t+n.

Cet investissement rapporte : (1+RY_,7)⁷.

> De choisir une stratégie de roulement (roll-over), en d'autres termes, une stratégie consistant à placer en t les titres de même maturité au taux rt. Ensuite, de réinvestir le tout en t+ 1 dans des obligations de même durée au taux rt+1 ; et ainsi de suite jusqu'à l'échéance. En somme, cet investissement en roulement rapporte à l'investisseur :

(1 + rt).(1 + rt+1)...(1 + rt+n-1)

En considérant l'investissement pour n périodes, la généralisation de l'équivalence entre ces deux stratégies nous donne la relation mathématique entre les taux de rendement longs et courts :

(1+Rt,n)ⁿ = (1 + rt) (1 + rt+1) ... (1 + rt+n-1)

? (1+Rt,n) = [(1 + rt) (1 + rt+1) ... (1 + rt+n-1)] 1/n, (2.2)

? Rt,n = [(1 + rt) (1 + rt+1) ... (1 + rt+n-1)] 1/n - 1, ?t, ?n.

Avec :

Rt,n : est le taux de rendement appliqué en t d'une obligation de maturité n ;

rt : est le taux de rendement observé en t sur le marché d'une obligation d'une échéance d'un (1) an ;

rt+1 : est le taux de rendement anticipé par le marché d'une obligation d'une échéance d'un an commençant à courir en t+ 1.

On en déduit qu'à l'équilibre, les taux longs Rt,n représentent une moyenne géométrique des taux courts observés rt et anticipés rt+1, rt+2,..., rt+n-1.

3.2.3. Exemple illustratif

En considérant deux périodes d'investissement, et en supposant que le taux au comptant à un an est de 6% et le taux anticipé dans un an est de 8%¹, alors le taux spot à deux ans est approximativement égal à 7%² . Ce résultat est obtenu par application numérique dans la formule générale (2.2).

3.2.4. Enseignements tirés de cette théorie

Les travaux de Lutz (1940) lui ont permis de dégager un résultat plus qu'essentiel : le niveau des taux longs s'explique par celui des taux courts. Par ailleurs, Trois enseignements fondamentaux viennent justifier la capacité de la théorie des anticipations à expliquer les variations des taux d'intérêt :

¹ On a supposé auparavant que les agents économiques sont capables d'anticiper les taux avec certitude.

² En général, pour des considérations liées aux marchés, on affiche des taux approximatifs (arrondis). Toutefois, dans ce cas, l'application numérique nous donnera exactement un taux de rendement de 6,995327%.

> Généralement, lorsque le marché tend à anticiper une hausse de taux d'intérêt, la courbe de taux prend une forme croissante. Réciproquement, lorsque le marché anticipe des taux futurs bas, la courbe sera décroissante.

> La structure par terme en univers certain révèle avec exactitude la façon d'évolution des taux d'intérêt. En d'autres termes, les taux à terme sont ceux anticipés par le marché.

> Cette théorie suppose que les titres de maturités différentes sont parfaitement substituables entre eux.

Depuis ces enseignements, on peut déduire que les résultats obtenus par Lutz sont totalement dépendants d'hypothèses que certaines sont on ne peut plus dire `irréalistes'.

3.2.5. Contraintes du modèle de structure de taux en avenir certain

Cette théorie a fait état de plusieurs critiques. D'ailleurs, beaucoup d'analystes sont venus renforcer les fondements essentiels des travaux de Lutz et ainsi apporter des corrections aux hypothèses qui frôlent l'irréalisme.

> La première des critiques a pour origine les professionnels des marchés. En effet, cette théorie présume que les investisseurs peuvent prédire les taux d'intérêt pour des périodes futures lointaines. A la frontière de l'inacceptable, l'investisseur pourra connaître les taux d'intérêt pendant une période future finie. Mais voilà justement, cette théorie tend vraiment à pousser les réalités jusqu'à l'absurde !

Cette critique trouve réellement sa justification du fait que le comportement des individus sur le marché est totalement contraire à la logique de l'hypothèse.

> Ensuite, vient Hickman (1943) qui démontra que les taux observés réellement et les taux prévus (tests effectués pendant une certaine période) n'étaient guère égaux. Bien plus encore, il y découvre un écart très important et surtout variable.

> Depuis, de nombreux tests effectués ont abouti aux mêmes conclusions. Toutefois, Meiselman (1962) est parvenu à modéliser le rôle des anticipations dans un monde incertain. Pour cela, il a porté son attention aux autres hypothèses, notamment celle supposant que les investisseurs n'ont pas d'aversion au risque, ce qui n'est pas totalement vrai en réalité.

Par ailleurs, le concept le plus marquant de cette théorie demeure le fait qu'elle paraît indépendante des théories traditionnelles. Ceci dit, Lutz n'a, dans aucune circonstance, invoqué les arguments les plus couramment utilisés tels que : la priorité au monde présent, la préférence pour la liquidité ou encore le risque en capital.

Ces critiques ont donné une autre formulation aux théories qui expliquent la structure par terme : il s'agit de l'analyse du modèle de structure par terme en univers incertain.

3.3. La structure de taux dans un univers incertain

Les travaux de Lutz et Hicks n'ont pas été suffisants pour expliquer la structure par terme de taux d'intérêt. Les défaillances des modèles d'analyse en environnement certain ont contribué de façon extraordinaire à l'exposition de plusieurs autres théories qui s'adaptent aux réalités des marchés financiers. La période des années soixante à soixante- dix a été des plus marquantes, appelée « l'âge d'or » où on a vu le concept d'incertitude s'introduire dans les différentes analyses.

Nous étudierons les principaux processus théoriques développés pendant ces années. 3.3.1. Rôle des anticipations en avenir incertain

La théorie exposée dans ce point est similaire au modèle de structure par terme en univers certain, sauf en ce concerne les anticipations des opérateurs de marché qui sont, cette fois, imprévisibles. Dans ce cas, il suffira de remplacer les taux courts anticipés rt+1, rt+2,..., rt+n-1 par leurs espérances mathématiques : E _(rt+1), E (rt+2),..., E (rt+n-1).

3.3.2. Principe du modèle

Pour Meiselman (1962), la théorie des anticipations en avenir incertain revient à reconsidérer la quatrième hypothèse proposée dans le cadre d'une structure par terme en monde certain, ce qui nous amènera à supposer que les agents sont, désormais, neutres envers le risque. A celle-ci, s'ajoute une cinquième hypothèse : celle de l'homogénéité des anticipations des agents économiques.

L'investisseur neutre envers le risque ne se préoccupe pas du risque de son investissement. Il aura tendance à vendre ses titres de plusieurs termes pour acquérir des titres courts. De ce fait, puisque tous les agents ont le même sens d'anticipation, on assistera incontestablement à une baisse des taux courts et hausse des taux à plusieurs périodes jusqu'à ce qu'il y ait équilibre entre les deux taux.

L'équilibre entre les deux stratégies d'investissement nous donne l'équation mathématique suivante¹ :

(1+Rt,n)ⁿ = (1 + rt) (1 + E (rt+1)) ... (1 + E (rt+n-1)) (2.3)

Cette équation définit les taux longs comme la moyenne géométrique du taux court actuel et des taux anticipés espérés.

3.3.3. Anticipation et incertitude : formes de la courbe de taux

Cette relation nous permet d'affirmer que cette théorie caractérisée par l'incertitude repose entièrement et exclusivement sur la nature de l'anticipation des agents économiques :

· Si les agents anticipent une hausse du taux puis une baisse, on aura une courbe « en cloche » ;

· Si les agents anticipent une hausse (resp. baisse) continuelle des taux, on obtient une courbe de taux croissante (resp. descendante) ;

· Enfin, si les agents ne prévoient aucun changement du niveau des taux d'intérêt, on obtient une courbe plate.

3.3.4. Contraintes de la théorie : incertitude et arbitrage

Le problème majeur que pose cette théorie est l'incertitude. En effet, le passage du modèle certain amène à changer les variables futures par leurs éléments aléatoires. Autrement dit, Dans un monde incertain, les prévisions sont approximatives telles qu'il existe des termes d'erreurs parmi les variables explicatives du modèle prévisionnel.

Toutefois, le fait d'aller jusqu'à dire que l'incertitude n'existe pas dans le monde financier s'avère être un immense exercice intellectuel qu'on ne pourra jamais résoudre !

En fait, les professionnels de marchés pensent que la théorie des anticipations en univers certain n'est autre que la dérivée (pas au sens mathématique) des théories projetées dans un monde incertain.

La justification vient du seul constat que seul le comportement arbitragiste contribue à la réalisation des gains. Dit autrement, il semblerait que la théorie des anticipations ait simplement cherché son indépendance des théories de l'intérêt ; Ceci dit, il lui a fallu recourir aux principes fondamentaux du modèle en univers certain, à savoir l'arbitrage, l'hypothèse de neutralité envers le risque ainsi que l'hypothèse d'homogénéité des anticipations.

Ces méditations nous permettent d'en sortir avec une conclusion très importante : c'est que si l'arbitrage permet à la théorie des anticipations de garder son autonomie, alors elle ne peut être des plus performantes d'autant qu'elle ne prend en aucun moment compte des conséquences imposées par le phénomène de l'incertitude. Ce qui nous amène à proposer d'autres théories pour expliquer la structure par terme de taux d'intérêt.

3.3.5. La théorie de la prime de liquidité

Hicks (1939) considère que les anticipations dans un monde incertain ne peuvent pas expliquer à elles seules la structure par terme de taux, il convient donc de prendre en compte les primes de liquidité, toutefois appelées primes de risque.

1. Exposé de la théorie

Cette théorie, contrairement à celle qui la précède, considère que l'investisseur a de l'aversion par rapport au risque. L'argument positif dans cette théorie est l'introduction du facteur risque afin de prendre en compte le comportement des agents face à ce risque. Les investisseurs qui souhaitent renouveler leurs placements exigeront une prime de risque (nécessairement positive) en vue de rémunérer le risque qu'ils encourent. Ainsi, la valeur des taux anticipés futurs est augmentée par la prime de risque pour chaque période de réinvestissement. A l'équilibre, nous obtenons la relation suivante :

(1+Rt,n)ⁿ = (1 + rt) (1 + E _(rt+1)+ ð1) ... (1 + E (rt+n-1)+ ðn-1) (2.4)

Où : ði : représente la prime de liquidité pour les périodes t+1, t+2, ..., t+n- 1.

A noter qu'en situation de stabilité de taux à court terme sur le marché, la courbe hicksienne n'est pas plate comme la courbe lutzienne, mais légèrement croissante, c'est en fait l'influence de la prime de risque qui en modifie à peine la forme de la courbe de taux.

2. Propriétés fondamentales de la théorie de la prime de liquidité

· Hicks a démontré le principe selon lequel les primes de liquidité augmentent avec l'horizon de détention des obligations. En d'autres termes, les prêteurs réclament des rémunérations de plus en plus grandes pour prêter de plus en plus long. On aura

ainsi : 0 < ð1 < ð2 <... < ðn-1

· Les titres de différentes maturités ne sont pas substituables, un titre à n périodes rapporte une rentabilité supérieure par rapport à la souscription de n titres successifs d'une période.

· Hicks a constaté que l'augmentation de la prime de liquidité se fait d'une manière

dégressive. Soit : ð2 - ð1 > ð3 - ð2>...> ðn-1 - ðn-2. La courbe obtenue sera effectivement croissante.

Cette théorie vient améliorer et compléter la théorie des anticipations. Cependant, elle a été soumise à un certain nombre de critiques considérant qu'elle est insuffisante lorsqu'il s'agit de déterminer la prime de risque.

D'autres théories ont été développées par la suite, qui viennent aussi compléter celles qui les précèdent.

3.3.6. La théorie de segmentation des marchés 1. Exposé de la théorie

La théorie de segmentation considère que les relations entre les différents compartiments des marchés sont motivées par des comportements prévisionnels. Ainsi, remettre en cause la prédominance de ces comportements serait une question d'existence de structure de taux.

Le premier à introduire la notion de marchés segmentés est Culbertson (1957) qui suppose que les choix des différents acteurs du marché ne sont pas principalement dus aux prévisions ; d'une manière plus empirique, il pose comme hypothèse que ce genre de comportement ne contribue que marginalement à l'explication de la courbe de taux. Cette motivation vient limiter la substituabilité des titres entre les marchés en se référant aux structures d'offre et demande des titres sur chaque échéance¹ :

· Un investisseur qui cherche à assurer son financement devrait aligner sa dette sur la période pendant laquelle ces fonds lui sont nécessaires, de ce fait, il aura tendance à éviter le risque d'émission de titres plus courts à des conditions incertaines ;

· De son coté, le prêteur choisira les titres lui assurant la disponibilité au bon moment.

Par ailleurs, les comportements de ces agents sont totalement semblables. En effet, Culbertson affirme que les agents ont pour principal souci d'égaliser la maturité de leur actif à celle du passif ; bien plus encore, il tente d'expliquer que cette attitude est celle de la plupart des institutions financières.

S'appuyant sur ces hypothèses, la théorie introduite par Culbertson tente d'expliquer la structure par le fait qu'il existe autant de marchés que d'échéances possibles où les taux d'intérêt tendent à ajuster l'offre et la demande de chacun.

2. Limites de la théorie

· Si les comportents spéculatif et prévisionnel permettent de définir et expliquer la structure de taux selon le comportement des agents, la séparation des marchés de titres de différentes maturités ne peut pas pousser les taux d'intérêt à varier dans le même sens, et ne donc peut expliquer la structure par terme de taux d'intérêt ;

· L'hypothèse d'une aversion absolue vis-à-vis du risque est assez excessive et dépourvue de fondements empiriques ;

· La théorie des marchés segmentés est difficilement soutenable d'autant qu'elle suppose que les agents préfèrent les maturités courtes ; mais surtout elle implique qu'un agent ne cherchera jamais à sortir de son compartiment même si les écarts de taux avec les autres compartiments sont importants.

C'est pour cela qu'on propose une autre théorie : la théorie de l'habitat préféré. 3.3.7. La théorie de l'habitat préféré

1. Exposition de la théorie

Cette théorie est présentée comme la synthèse des deux théories qu'on vient de présenter. En effet, elle définit une position intermédiaire car elle prend en compte l'hypothèse des marchés segmentés et le fait que les comportements des agents soient influencés par des primes de liquidité en vue de se prémunir contre le risque de taux.

Cette théorie est présentée pour la première fois par Modigliani et Sutch (1966, 1967 et 1969) : « La théorie de l'habitat est à la base une adaptation de la théorie des anticipations de la structure des taux d'intérêt en incertitude, dans un monde où (1) les taux futurs sont en fait incertains ; (2) les échangistes, tant détenteurs finals de richesse qu'emprunteurs finals, ont des préférences définies par rapport à la longueur de la période de temps pour laquelle ils veulent garder leurs fonds investis, ou pour laquelle ils ont besoin d'un financement (c'est-à-dire qu'ils ont un habitat de maturité préférée) ; et (3) les deux types d'échangistes font preuve généralement d'une aversion pour le risque, et, par conséquent, toutes choses égales par ailleurs, préféreront faire coïncider les maturités de leur portefeuille avec leur habitat, de façon à être certains des rendements ou des coûts. En plus de ces échangistes finals, le modèle reconnaît également l'existence d'arbitragistes, ou d'intermédiaires, préparés simultanément à prêter et emprunter dans des maturités différentes, quand la différence entre les rendements anticipés est assez attrayante pour compenser le risque encouru dans l'opération. » (Modigliani et Sutch [1967, p.569]).

2. Propriétés de la théorie

Ainsi, Modigliani et Sutch ont eu pour idée que les préférences des agents et leurs besoins les obligent à choisir un habitat, c'est-à-dire un compartiment particulier de la courbe de taux. Ils affirment aussi que ces agents n'accepteront pas de s'engager dans une opération risquée sauf pour un rendement supplémentaire définit par une prime de liquidité. Dans ce cas, cette opération est dite « risquée » pour l'agent du moment qu'il acceptera d'investir dans des titres dont la maturité est différente de sa maturité préférée.

Selon l'analyse, les décisions des agents sont influencées simultanément par les anticipations et par la position de l'habitat sur le marché. Le taux d'intérêt résulte de l'équilibre entre l'offre et la demande de l'habitat correspondant, on retrouve donc l'idée de segmentation de Culbertson sauf que dans ce cas l'agent peut sortir de son habitat moyennant une prime.

Soit la formule obtenue :

(1+Rt,n)ⁿ = (1 + rt) (1 + _rt+1+ ð1) ... (1 + rt+n-1+ ðn-1) (2.5)

Où : ði : représente la prime de risque supposée stable dans le temps.

Les travaux de Modigliani et Sutch ont donné une approche théorique significative en matière de taux d'intérêt. Ils signalent ici l'importance du comportement des agents face au risque et la contribution de l'équilibre entre offre et demande dans l'explication des variations des taux d'intérêt.

Nous avons tenté d'expliciter les théories traditionnelles qui permettent d'expliquer la structure par terme de taux d'intérêt. Nous constatons l'importance de l'incertitude dans la compréhension des variations des taux.

En fait, certaines de ces théories imposent parfois des positions extrêmement éloignées des pratiques des marchés financiers.

En premier, la théorie des anticipations occupe la position la plus extrême quant elle introduit le fait que l'incertitude ne modifie pas vraiment les effets en environnement certain. De l'autre coté, la théorie de segmentation des marchés affirme que les anticipations des agents ne constituent même pas un facteur dans le comportement spéculatif.

Enfin, la théorie de l'habitat préféré constitue plutôt la médiane entre ces deux théories. L'attitude des agents envers le risque impose la présence de prime de liquidité constituant le principal facteur explicatif de la théorie de la prime de liquidité. Aussi, les anticipations et la position de l'habitat de l'agent sur la maturité laissent dire que ces deux dernières théories constituent en quelque sorte la synthèse des autres théories.

Chacune des théories a fait part à de nombreuses critiques et reproches quant à leur capacité d'expliquer les mouvements des taux sur les marchés. Néanmoins, leur importance a été d'un grand bénéfice puisqu'elles sont beaucoup utilisées en théorie financière.

Par ailleurs, nous avons abordé, dans ce chapitre, l'importance des outils actuariels non seulement dans la mesure des risques liés aux obligations mais aussi leur pertinence dans l'évaluation des titres en particulier et des portefeuilles d'obligations en général.

La gestion obligataire ne touche pas uniquement ces outils, en effet, la troisième étape de toute gestion de portefeuille obligataire consiste en l'élaboration de stratégies efficaces en vue d'en tirer les meilleures décisions d'investissement possibles. Il s'agit donc d'étudier ce point dans le prochain chapitre de cette première partie.

Ce présent chapitre est composé de deux sections :

Section 1 : Les stratégies actives de gestion obligataire Section 2 : Les stratégies passives de gestion obligataire

Tous les points traités à travers le chapitre précédent ne constituent, en fait, que la matière première de toute gestion obligataire. En effet, un gérant de portefeuille obligataire doit, non seulement maitriser les outils actuariels, savoir évaluer ses obligations ou encore pouvoir réprimer le risque de taux dans un univers d'incertitude soit pour avoir des rendement les plus favorables possibles ou bien éliminer, si c'est possible, ce risque en fonction d'un certain taux de rendement, mais celui-ci doit savoir établir une démarche cohérente de la gestion obligataire en s'appuyant sut tous les aspects et concepts techniques de la gestion de portefeuilles.

Du processus de gestion obligataire découle au final une décision stratégique en fonction d'un certain rendement et risque souhaités. C'est une étape primordiale que tout gérant obligataire doit entreprendre en vue de réaliser ses objectifs.

Les analystes financiers proposent deux méthodes de gestion : les stratégies actives et les stratégies passives. Elles seront développées dans ce chapitre après avoir fait le point brièvement sur les étapes du processus de gestion d'un portefeuille obligataire.