2.5. La duration d'un portefeuille obligataire
Un portefeuille est composé de titres, et étant
donné que chaque titre a une duration, il en existe forcément une
duration pour une masse de titres. Celle-ci est égale à la
moyenne pondérée des durations des titres individuels qui
composent le portefeuille. Les poids pris en considération sont les
valeurs présentes des titres (valeur totale + intérêts
courus) rapportées à la valeur globale de l'ensemble des
titres.
Supposons un portefeuille P, composé de
k titres ayant chacun une valeur de marché Vi,
la valeur du portefeuille est : k
Vp = ? Vi
i =1
2.5.1. Calcul de la duration (D) d'un
portefeuille
k
La proportion des titres dans le portefeuille est
de : wi = V i / Vp tel que : ?
wi = 1.
i = 1
Hypothèse : En
considérant que la courbe des taux est plate, donc que les taux
d'intérêt
évoluent en constance pendant toute la
période de placement, et soit dr la variation
de
taux d'intérêt. La variation de la valeur du
portefeuille sera donc de :
k k
dVp ? dVi
k?4
dVi/Vi

:
dVp = ? dVi. Ce
qui nous donnera = ... (3)
Vp Vp Vp/Vi
i=1 i =1 i =1
La variation relative des titres :
En reprenant la formule (2)
représentant l 'Elasticité
dv +r
en fonction de la duration, on aura : i = --
Di .d
Vi (1(l+r))
La variation relative de la valeur du portefeuille :
s'obtient en remplaçant cette dernière formule
dans l'expression (3), soit :
d(1+r)
dVp
Vp
= (-13L( 1+r )K
i =1 Vp/Vi
k
= E - wi . Di. [d (1+r)/
(1+r)]
i =1
Rappelons aussi que l 'Elasticité est la variation
du prix par rapport à la variation du
taux d'actualisation (1+ r), ce qui nous donne la Duration
D du portefeuille (au signe
k
près) qui s'exprime comme suit : D
= - dVP/VP= ? wi. Di qui
représente
d(1+r)/(1+r) i = 1
effectivement la moyenne pondérée des durations
de titres qui composent le portefeuille. 2.5.2. La
sensibilité (S) d'un portefeuille :
1
Sachant que la sensibilité peut s'écrire en
fonction de la duration soit : S = - .
D.
(1+r)
En remplaçant cette formule dans l'expression de la
duration d'un portefeuille, nous
aurons : - S. (1+r) = - ? wi . Si .
(1+r).
D'où :
S = ? wi .
Si
i
En effet, cette formule montre que les caractéristiques
de la duration peuvent aussi s'appliquer à la sensibilité du
portefeuille qui est donc égale à la moyenne
pondérée des sensibilités des différents titres
composant le portefeuille.
3. La convexité : (bond
convexity)
Pour une variation importante de taux d'intérêt,
la sensibilité fournit une variation des prix des obligations non
suffisamment précise ; en effet, la réalité du
marché nous laisse dire que la sensibilité,
représentée par une fonction de dérivée
première, ne donnera une bonne approximation des prix que pour des
variations infinitésimales des taux d'intérêt. Donc, le
recours à une méthode précise impose l'application d'un
terme de second ordre, négligeable pour des petites variations de taux
d'intérêt. Cet élément suppose que la relation qui
lie le prix et le taux de rendement d'une obligation n'est pas linéaire
mais plutôt convexe ; d'où le concept de
`convexité`.
3.1. Définition de la convexité
La convexité est la dérivée seconde du
cours d'une obligation par rapport au taux d'intérêt. Elle mesure
la variation relative de la sensibilité d'une obligation pour la petite
fluctuation des taux d'intérêt. Par ailleurs, la convexité
exprime la rapidité de l'appréciation et la lenteur de la
dépréciation du cours de l'obligation si les taux baissent ou
montent respectivement.
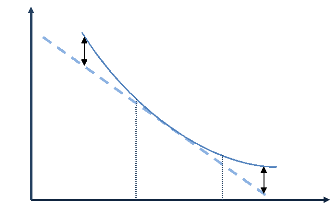
La mesure approximative par la sensibilité fournit une
valeur différente du prix exact de l'obligation, en fait c'est un
prix `approximatif'. Sur le graphique ci-dessous, on
peut lire l'écart obtenu entre le prix calculé et le prix exact
de l'obligation :
r
r1
ro
Po
P1
P(r)
Graphique n° 2 : Illustration de l'écart
entre le prix calculé et le prix exact
En utilisant le théorème de développement de
Taylor1, on peut approcher la variation du prix
d'une obligation en fonction de son taux actuariel (r) :
P(r) '' P(r0) + P'(r0).(r-r0)
+
P(2) (r) j (r-r0)2 +
E
2 I)(r)

Avec : P (r) : le prix de l'obligation
P' (r) = dP(r)
dr , variation du prix par rapport au
taux d'intérêt
;P(2) (r) =
d2 P dr(r)
,
dérivée seconde prix de l'obligation.
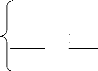
2)
Sachant aussi que : dP(r)
e=, P'(r0) dr + P2( I)(r())
dr2
dP(r)
(r)
I)/ (r)
eS.I
IS.I
d + P(2) (r) d
2
I)(r) r 2 I)(r) r
On peut écrire:
P(2) (r) 2

dP(r) - S dr + dr
P) 2 I)(r)
Or, la convexité (C) est définie comme le moment de
second ordre de la variation des
prix par rapport au taux d'intérêt : C
=
P(r)
P(2) (r)
dP(r) = - S dr +
P(r)
Ce qui nous amène à :

C
2

dr2
Ou encore en appliquant la définition à la valeur
actualisée, on aura ainsi :
1
Convexité = In (ti (1+ti) Fi)
P
.(1+
r
)
2
i
=
1(1+
r
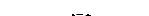
)ti
Cette formule permet de déduire que plus la
convexité est grande, le prix diminue lentement pour une hausse de taux
et que si les taux baissent le prix du titre subit une augmentation
sensible.
Les propriétés de la duration sont applicables
à la convexité, celle-ci est d'autant plus grande que la
maturité de l'obligation est longue et le coupon faible. Cependant, et
comme nous le montre le graphique 2, la convexité
fournit une meilleure approximation du cours de l'obligation pour les
variations de taux d'intérêt limitées, et cette
précision sera d'autant plus importante si on considérait les
autres termes du développement de Taylor.
3.2. Convexité d'un portefeuille
La convexité Cp du
portefeuille obligataire est définie comme la moyenne
pondérée des convexités Ci des
k titres qui le composent. Elle a pour
formule1 :
k
Cp = E wi x
Ci
i=1
Où : wi désigne le poids
de la valeur de (Vi) marché de l'obligation i
rapporté à la valeur du portefeuille
P.
4. Les limites des outils d'analyse
actuariels
> Taux de rendement et réinvestissement des
coupons
La formule du taux de rendement actuariel suppose que les
coupons sont réinvestis au même taux, chose qui est peu
évidente sur un marché. En effet, cette hypothèse ne prend
pas en compte les fluctuations régulières des taux.
1 La démarche de construction
de la formule a été illustrée précédemment
dans la page 43.
> La duration est un instrument de mesure performant pour
les obligations à taux fixe et remboursables in fine.
Cependant, cet outil est insuffisant pour les autres types de titres ;
> Les outils actuariels supposent généralement
que la courbe des taux est plate et ne tiennent pas compte des mouvements de
cette courbe ;
> La duration ne peut être utilisée comme
outil performant pour la mesure de la sensibilité d'une obligation au
taux d'intérêt, que dans le cas d'une variation importante de taux
d'intérêt, à défaut c'est la convexité qui
est prise en compte.
Nous avons passé en revue les outils permettant
à un gestionnaire d'avoir une simple idée sur la valeur actuelle
de ses titres et d'en projeter les perspectives de gain ou de perte. Ces outils
sont très simples à développer, mais contiennent beaucoup
de lacunes, chose qui n'empêche guère les analystes à les
utiliser tant leur importance les a rendus indispensables dans toute
évaluation obligataire.
En effet, l'évaluation des obligations et d'un
portefeuille d'obligations reposent beaucoup sur ces outils, cette analyse fera
l'objet de développement dans la prochaine section.
Par ailleurs, nous avons vu que l'inconvénient
majeur des outils actuariels est le principe de constance du taux de rendement
actuariel dans le temps, nous ne pouvons donc pas avancer sans pallier à
cette limite à travers l'analyse de la courbe des taux
d'intérêt, qui fera également l'objet de la deuxième
section de ce chapitre.
| 


