Utilisation des méthodes d'optimisations métaheuristiques pour la résolution du problème de répartition optimale de la puissance dans les réseaux électriques

République Algérienne Démocratique et Populaire

Ministère de l'Enseignement Supérieure et de la Recherche Scientifique
Centre Universitaire d'El-oued
Institut de Sciences et Technologie

N° Ordre : ...............
Série : .....................

MEMOIRE

Présenté pour obtenir le diplôme de

Magister en Electrotechnique
Option : Réseaux Electriques
Par
GACEM Abdelmalek

Utilisation des Méthodes d'Optimisations

Métaheuristiques Pour La Résolution Du Probleme De

Répartition Optimale De La Puissance Dans les Réseaux

Electriques

Soutenu le 24/06/2010

Devant le jury composé de :

M. SERAIRI Kamel P.R Universitaire de Biskra Président

M. BEN ATTOUS Djilani M.C Centre Universitaire d'El-oued Rapporteur

M. MIMOUNE Med Souri P.R Universitaire de Biskra Examinateur

M. BENCHOUIA Med Toufik M.C Universitaire de Biskra Examinateur

ãÜÜÜíÍÑáÇ ?????? ?? ???

R e m e r c i e m e n t s

Je remercie tout particulièrement Dr BENATOUS Djilani pour m'avoir encadré, ainsi que leurs nombreux conseil, suggestions et encouragements.

Merci également à tous les membres de jury de thèse et tous les participants

Finalement, je tiens à remercier ma famille pour son soutien constant tout au long de mes études.

Utilisation Des Méthodes D'Optimisations Métaheuristiques Pour La Résolution
Du Problème De Répartition Optimale Des Puissances Dans Les Réseaux
Electriques

Résumé

Le calcul de la répartition optimale de la puissance ou l'écoulement de puissance optimal, au niveau d'un réseau électrique, emploie des techniques de programmation mathématiques standard. Parfois ces techniques ne sont pas convenables pour traiter certaines considérations pratiques rencontrées dans les systèmes de puissance, telle que l'incertitude des contraintes de fonctionnement.

On propose dans ce travail l'application des méthodes métaheuristiques inspirées de la nature sont considérées comme méthodes qui peuvent trouvées des solutions optimales globales ou quasi globales .On a choisie l'optimisation par Essaims de Particules, les algorithmes génétiques et la méthode Monte Carlo pour la répartition optimale des puissances dans les systèmes électriques.

Les résultats numériques de test montrent que cette méthode est prometteuse et possède une grande flexibilité pour le traitement les problèmes très complexe et les contrainte multi objectif.

S O M M A I R E

LISTE FIGURE 8

LISTE TABLEAU 9

INTRODUCTION GENERALE 11

CHAPITRE I 13

I-1 Introduction 14

I-2 Modélisation des éléments du réseau électrique 14

I-2.1 Générateur de puissance 14

I-2.2 Ligne de transport 15

I-2.3 Charge électrique 16

I-2.4 Elément shunt 16

I-3 Classification des variables des équations de R.C 16

I-3.1 Variables de perturbation (Variables contrôlées) 16

I-3.2 Variables d'états 16

I-3.3 Variables de contrôle. 17

I-3.4 Classification des jeux de barre 17

a) Jeu de barre de référence 17

b) Jeu de barre générateur 17

c) Jeu de barre de charge 17

I-4 Les équations de l'écoulement de puissance 17

I-4.1 Les équations aux J.d.B de charge 17

I-4.2 Exemple d'un système à deux J.d.B 18

I-4.3 Calcul de la puissance au niveau de J.d.B 20

I-4-4 Les équations d'écoulement dans les lignes 20

I-4-5 Les pertes de puissance dans lignes 21

I-6 Résolution des équations de l'écoulement de puissance 22

I-6.1 Méthode de Newton-Raphson 22

I-6.2 Application de la méthode de N-R, au problème de l'écoulement de puissance 23

I-6.3 Détermination des sous matrices de la Jacobienne J 25

I-6.4 Remarques 26

I-6.5 Algorithme de Newton-Raphson 26

I-10 Application Newton-Raphson à un réseau de six JDB 27

I-11 Influence d'une consommation excessive de réactif au bus 6 28

I-12 But du banc de capacités 29

I-13 Conclusion 30

CHAPITRE II 31

II.1 Introduction 32

II-2 Architecture des réseaux électriques 33

II.3 Stratégie du fonctionnement des Centrales électriques 33

II.3.1 Unités de charge de base 34

II.3.2 Unités intermédiaires 34

II.3.3 Unités de pointe 34

II.3.4 Unités de réserve 35

II.4 Dispatching Economique 35

II.5 Formulation mathématique du problème du Dispatching Economique 37

II.5.1 La méthode Lambda 38

II.5.2 Solution du problème du Dispatching Economique sans pertes 40

II.5.3 Solution du problème Dispatching Economique avec considération des pertes 41

Remarques 42

II- 6 Classification des méthodes d'optimisations 43

II- 6. 1 Méthodes déterministes « locales » 44

II-6. 1. 1 Les méthodes de gradient 44

Algorithme de la plus forte pente 45

II- 6. 1. 2 La méthode de Newton 45

Développement du Lagrangien, du Gradient et du Hessien 45

Algorithme 46

II- 6. 2 Les méthodes métaheuristiques (globale) 47

II- 6. 2. 1 Mante Carlo 47

Algorithme 47

II- 6. 2. 2 Recuit Simulé 48

II- 6. 2. 2. 1 Température initiale 48

II - 6. 2. 2. 2 Modification élémentaire 48

II - 6. 2. 2. 3 Paramètres 48

II - 6. 2. 2. 4 Algorithme 49

II-6. 2.3 La méthode tabou 49

- Principe 50

- Les tabous 50

- Algorithme 50

II- 6. 2. 4 Les méthodes évolutionnistes 51

II- 6. 2. 4. 1 Stratégies d'Evolution (ES) 52

II- 6. 2. 4. 2 Programmation Génétique (GP) 52

II- 6. 2. 4. 3 Programmation Evolutionnaire (EP) 52

I-7 Conclusion 53

CHAPITRE III 54

III - 1 Introduction 55

III -2 Les algorithmes génétiques 55

Principe 56

III - 2.1 Codage des chromosomes et décodage 56

III -2.1.1 Codage binaire 56

III -2.1.2 Codage de gray 57

III -2.1.3 Codage dynamique des paramètres 58

III -2.1.4 Codage réel 59

III - 2.2 Fonction d'évaluation 59

III - 2.3 Sélection 60

III - 2.3.1 La loterie biaisée ou roulette Wheel 60

III - 2.3.2 La méthode élitiste 61

III - 2.3.3 La sélection par tournois 61

III - 2.3.4La sélection universelle stochastique 61

III - 2.4 Le croissement 61

III - 2.4.1 Croisement en un point 62

III - 2.4.2 Croisement en un et deux points 62

III - 2.4.3 Croisement uniforme 63

III - 2.5 Mutation 63

III - 2.6 Organigramme de la procédure génétique 64

III - 2.7 Application de l'AG à la répartition économique des puissances 64

III - 2.7.1 Codage des chromosomes et le décodage 65

III- 2.7.2 Tirage et évaluation de la population initiale 67

III-2.7.3 Sélection 68

III-2.7.4 Croisement 68

III-2.7.5 Mutation 68

III-2.7.6 Retour à la phase d'évaluation 69

III- 3 Optimisation par essaim particulaire 70

III-3.1 Principe Caractéristiques 70

III -3.2 Topologie du voisinage 71

III-4 Formalisation et programmation 73

III-4.1 Initialisation de l'essaim et Nombre de particules 73

III-4.2 Coefficient de constriction 74

III-4.3 Facteur d'inertie 74

III-5 Algorithmes 76

III-6 Avantages de L'OEP 77

III-7 Conclusion 77

CHAPITRE IV 78

IV- Application et Simulation 79

IV-1 Introduction 79

IV-2 Optimisation de fonction de coût 79

IV-2.1 Test de l'algorithme Génétique 80

Paramètres A-G 80

IV-2.2 Réseau test à 6 jeux de barres 80

IV-2.3 Réseau test à 25 jeux de barres 82

IV-2.4 Réseau test à 30 jeux de barres (IEEE 30-bus) 86

Convergence de l'Algorithme Génétique 87

IV-2.5 Test de l'algorithme OEP 87

Paramètres OEP 87

Convergence de l'Algorithme ESSAIMS PARTICULES 88

IV-3 Optimisation de perte 91

IV-4 Test sur la fonction multi objective 92

IV-5 Conclusion 93

CONCLUSION 95

Annexe A 97

Bibliographie 102

L i s t e de s f i g u r e s

Figure I-1 : Modèles d'un générateur 15

Figure I-2 : Modélisation des lignes et des câbles par un schéma en Ð équivalent . 15

Figure I-3 : Modèle d'une charge électrique sous forme d'une impédance constante... 16

Figure I-4 : système à deux J.d.B 18

Figure I-5 : Organigramme simplifié de l'algorithme de Newton-Raphson 26

Figure I-6 : Schéma unifilaire du réseau électrique à 6 jeux de barres . 27

Figure I-7 : Convergence de l'algorithme N-R pour le réseau électrique à 6 JDB 28

Figure I-8 : Chute de tension sur le J.B 6 . 29

Figure I-9 : Influence de la compensation la tension 29

Figure II-1 : Stratégie de fonctionnement des centrales suivant la demande de 34
puissance électrique

Figure II-1 : Modèle du système électrique utilisé dans le dispatching économique 36

Figure II-2 : Courbe de coût typique (entrée-sortie) d'un générateur 36

Figure II-3 : Courbe typique de l'accroissement du coût de combustible 37

Figure II-4 : Organigramme de la méthode lambda 40

Figure II-5 : Classification des méthodes d'optimisations 43

Figure II-6 : Organigramme simplifié de l'algorithme de Newton 46

Figure II-7 : Organigramme de la méthode Monte Carlo 47

Figure II-8 : Organigramme de l'algorithme du recuit simulé 49

Figure II-10 : Organigramme de l'algorithme de tabou simple .. 51

Figure II-11 : Principales catégories des Algorithmes Evolutionnaires 51

Figure III-1 : Sélection par la méthode de la roue de loterie 60

Figure III-2 : Principe de croissement en un point . 62

Figure III-3 : Principe de croissement en deux points 62

Figure III-4 : Croisement uniforme . 63

Figure III-5 : Opérateur de mutation 63

Figure III-6 : Organigramme d'un algorithme génétique 64

Figure III-7 : Schéma unifilaire de réseau électrique . 65

Figure III-8 : Schéma de principe du déplacement d'une particule . 71

Figure III-9 : (a) anneau (avec n = 2), (b) rayon, (c) étoile . 72

Figure III-10 : Influence d'inertie linéairement et sigmoid 75

Figure III-11 : Organigramme d'OEP 76

Figure IV-1 : Schéma unifilaire du réseau électrique à 6 jeux de barres 81

Figure IV-2 : Schéma unifilaire du réseau électrique à 25 jeux de barres .. 82

Figure IV-3 : Puissances actives générées du réseau électrique à 25 jeux de barre 84

Figure IV-4 : Comparaison des puissances du réseau électrique à 25 jeux de barre 85

Figure IV-5 : Comparaison des puissances du réseau électrique à 25 jeux de barre 86

Figure IV-6 : Evolution progressive de la fonction coût de l'AG - Binaire 87

Figure IV-7 : Evolution progressive de la fonction coût de l'AG - Binaire 88

Figure IV-8 : Modules des tensions du réseau électrique à 30 jeux de barre .. 90

Figure IV-9 : Phases des tensions du réseau électrique à 30 jeux de barre.................. 91

L i s t e D e s T a b l e a u x

Tableau I-1 : Tension et puissance au niveau de J.D.B 27

Tableau I-1 : Puissances transmises et pertes dans les lignes 28

Tableau I-1 : Résume la solution obtenue par N-R 28

Tableau III-1 : Code binaire et code gray sur 4 bits 58

Tableau III-2 : Ensemble des paramètres des puissances actives générées PGi 65

Tableau III-3 : Codage de l'ensemble des paramètres de PGi 66

Tableau III-4 : Processus de la première génération de l'AG pour le réseau 9 67 noeuds

Tableau III-5 : Nouvelle Population 68

Tableau III-6 : Résultats de croisement pour deux locus différents 68

Tableau III-7 : Mutation avec simple tirage aléatoire pour chaque bit entre 0 et 1 .. 69

Tableau III-8 : Nouvelle valuation 69

Tableau IV-1 : les opérateurs de l'AG - Binaire 80

Tableau IV-2 : Les données des fonctions de coût des 3 générateurs du réseau 6 bus .. 80

Tableau IV-3 : Tensions du réseau électrique à 6 J.B 81

Tableau IV-4 : Puissances et coûts de production du réseau électrique à 6 J.B 82
Tableau IV-5 : Les données des fonctions de coût des 3 générateurs du réseau 6 bus. 83
Tableau IV-6 : Tensions du réseau électrique à 25 J.B .. 83

Tableau IV-7 : Puissances et coûts de production du réseau électrique à 25 J.B . 84

Tableau IV-8 : Comparaison des puissances et coûts de production du réseau électrique à 85

25 J.B

Tableau IV-9 : Les données des fonctions de coût des 6 générateurs du réseau 30 bus 86

Tableau IV-10 : les paramètres de l'OEP 88

Tableau IV-11 : Tensions du réseau électrique à 30 J.B .. 89

Tableau IV-12 : Puissances et coûts de production du réseau électrique à 30 J.B . 90

Tableau IV-13 : Puissances et coûts de production du réseau électrique à 30 J.B . 92

Tableau IV-14 : Puissances et coûts de production du réseau électrique à 30 J.B 93

INTRODUCTION

Introduction

1 Introduction

Le rôle principal de toute entreprise chargée de la production d'énergie électrique est d'assurer à

tout moment, et en tout lieu, la couverture des demandes des utilisateurs en puissances actives et réactives. L'entreprise doit en outre garantir une qualité acceptable de la puissance avec un coût d'exploitation réduit. Pour bien exploiter un réseau électrique donné, il faut tout d'abord résoudre les problèmes d'ordre technique et économique. Souvent, on se trouve confronté à un problème, qui est celui de la répartition économique des puissances. Au début, la solution utilisée consiste à charger ou à faire produire au maximum les unités ayant le meilleur rendement. Cette solution n'est pas rentable puisque l'abus de fonctionnement des machines diminue leurs durées de vie et par conséquent, les frais d'entretien et de maintenance augmentent considérablement. L'extension et la complexité du réseau, laisse le choix aux chercheurs pour le développement de nouvelles méthodes afin de contribuer à l'allégement de ce problème.

Le problème de la répartition économique d'énergie a pris une importance considérable avec l'apparition de la crise d'énergie nécessitant des combustibles de plus en plus chers. Il faut donc planifier les puissances actives et réactives de chaque centrale électrique, de telle sorte que le coût total de fonctionnement du réseau entier soit minimal. D'une autre façon, il faut varier les puissances actives et réactives des générateurs dans certaines limites afin de satisfaire la demande particulière de la charge avec un coût minimal du combustible. Ce processus est appelé l'écoulement de puissance optimal, et parfois, il est connu comme le problème du dispatching économique.

La complexité des problèmes d'optimisation de l'écoulement de puissance dans un réseau électrique surtout avec la dérégulation du marché d'électricité et le développement de la production décentralisée fait en sorte qu'il est souvent difficile d'utiliser des méthodes exactes d'optimisation compte tenu du manque de flexibilité des méthodes classiques pour intégrer diverses contraintes spécifiques. Les métaheuristiques constituent alors une stratégie de résolution de plus en plus privilégiée .

Les nombreuses métaheuristiques sont inspirées par analogie avec la biologie des organismes. Ainsi, les théories de l'évolution ont inspiré les algorithmes évolutionnaires, les phénomènes de suivi de piste chez les fourmis ont conduit à l'élaboration des algorithmes de colonies de fourmis,

l'étude de l'organisation de groupes d'animaux a donné naissance aux méthodes d'optimisation par essaims particulaires.

L'objectif principal de ce travail est l'étude et l'analyse de la répartition optimale de puissance. La fonction objective qu'on veut minimiser est la fonction coût de production des puissances actives des générateurs. L'optimisation par essaims particulaires (OEP) (Particle Swarm Optimization) a été appliquée pour la résolution de ce nouveau problème d'optimisation. Les méthodes proposées ont été simulées dans l'environnement Matlab, et testées sur plusieurs réseaux standard. Ainsi en évalué de la performance de la méthode étudiée par la variation des variables de commande de cette méthode et la présentation des recommandations concernant la performance de cette méthode et comparai des résultats obtenus par la méthode OEP avec d'autres méthodes classiques et métaheuristiques. Afin en tenant compte des pertes de puissance active et les déviations des tensions aux niveaux des jeux de barres.

Ce travail commence par une introduction générale sur le problème de la répartition optimale de la puissance. Le premier chapitre présente la description et la modélisation des éléments de puissance essentiels du réseau de transport ainsi que la formulation du problème de l'écoulement de puissance. Le deuxième chapitre présente le problème de l'optimisation de l'écoulement de puissance ainsi qu'un ensemble de méthodes d'optimisation utilisées pour résoudre ce problème d'optimisation. Dans le troisième chapitre nous avons exposé l'application en détaille de la méthode génétique et l'optimisation par essaims de particules au problème de l'écoulement de puissance optimal. Le quatrième chapitre contient un ensemble de tests sur des réseaux électriques standard, avec des résultats numériques. Ces résultats sont dûment commentés et analysés.

Finalement nous terminerons ce mémoire par une conclusion et différentes perspectives de recherche qui nous semblent intéressantes pour la continuité de ce travail.

CHAPITRE I

Répartition de charge

électrique

I- Répartition de charge électrique

I-1 Introduction

La répartition des charges (load flow ou power flow) est l'un des principaux problèmes qui se pose aux gestionnaires d'un système de production - transport d'énergie électrique. Dans tout ensemble de centrales électriques alimentant un ensemble de consommateurs par l'intermédiaire d'un réseau de transport maillé, on doit déterminer la répartition des puissances fournies par ces centrales à un instant donné tout en respectant un ensemble de contraintes techniques et économiques.

La résolution du problème de la répartition des charges, nous permet de déterminer les valeurs du module et de la phase de la tension en chaque noeud du réseau pour des conditions de fonctionnement données. Ce qui nous permettrons de calculer les puissances transitées et générées et les pertes. Pour résoudre ce problème, il est nécessaire de déterminer les conditions de l'opération en régime permanent, d'un système de puissance, qui sont [01] :

> La formulation d'un modèle mathématique appropriée.

> La spécification d'un certain nombre de variables et de contraintes dans les noeuds du système.

> La résolution numérique du système.

I-2 Modélisation des éléments du réseau électrique

Un réseau de distribution électrique contient un ensemble de composants qu'il faut modéliser pour pouvoir établir les équations qui régissent le comportement du système.

Les éléments qui interviennent dans le problème de répartition de charge sont ceux qui sont exposés à des hautes tensions et à des forts courants, à savoir : générateurs de puissance (machine synchrone), charges électriques, lignes de transports, transformateurs de puissances et compensateurs statiques [02].

I-2.1 Générateur de puissance

Dans l'analyse de l'écoulement de puissance, les générateurs sont modélisés comme des injecteurs de courants. Dans l'état stationnaire, un générateur est généralement contrôlé de sorte que la puissance active (P_g ) injectée au jeu de barre et la tension aux bornes du générateur soient

maintenues constantes [03] [02].

La puissance active du générateur est déterminée par le contrôle de la turbine, qui doit être dans la capacité du système turbine - générateur. La tension (V_g ) est principalement déterminée par

l'injection de la puissance réactive au jeu de barre de production [02].

ä i

V i

Figure I-1 : Modèles d'un générateur

I-2.2 Ligne de transport

Une ligne électrique entre les noeuds i et j sera donc représentée par le schéma en ð comme

indiqué sur la figure (I-2) comprenant une impédance série ou longitudinale Z ij = R _ij + jX _ij (avec Rij ^et X_ij respectivement résistance totale et inductance totale de la ligne) et une admittance en parallèle y 10 = y₂₀ = ( G + jB) / 2 , avec (G et B étant respectivement la conductance totale et la susceptance totale d'ordre direct de la ligne) [04].

Les pertes transversales par effet couronne dans le cas des lignes de transport sont négligeables. Il n'y a donc pas de courant résistif dérivé et on admet que la conductance transversale G est nulle.

y1 0

Z=R+jX

y20

Figure I-2 : Modélisation des lignes et des câbles par un schéma en Ð équivalent

X₁ ä₁

X X₂ ä₂

X₃ V 1

X₄ V₂

I-2.3 Charge électrique

La charge électrique est souvent modélisée sous forme d'une impédance constante. La plupart des charges représentent une sous-station (système de distribution). Ces charges sont connectées au réseau électrique à travers un transformateur à prises de charges variables, où le niveau de tension de la charge est maintenu pratiquement constant. Dans ce cas, les puissances actives et réactives de la charge peuvent être représentées par des valeurs constantes.

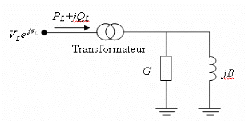
Figure I- 3 : Modèle d'une charge électrique sous forme d'une impédance constante

I-2.4 Elément shunt

Dans la plupart des cas, les éléments shunt sont les batteries de condensateurs et les réactances qui sont utilisés pour fournir ou absorber la puissance réactive afin d'obtenir un meilleur profil de tension [02].

I-3 Classification des variables des équations de R.C I-3.1 Variables de perturbation (Variables non contrôlées)

Ce sont les puissances P D 1 , P _D2 , QD1, QD2 demandées par les charges.

P 1		P D				1
P	P2		P D			2
Q 1				QD			1
Q 2					QD		2

I-3.2 Variables d'états.

Ce sont les variables :( V₁ , V ₂ , ä₁, ä₂) Soit X un vecteur appelé vecteur d'état :

I-3.3 Variables de contrôle.

Ce sont les puissances de source P g 1 , P_g2 , Qg1 ,Qg2 .

U₁ P_g 1

U U₂ P_g 2

U₃ Q_g 1

U4

Qg

2

I-3.4 Classification des jeux de barre.

Pour chaque jeu de barre, deux variables doivent êtres spécifiées au préalable et les deux autres sont à calculer. Donc, on peut classer les jeux de barres comme suit

a) Jeu de barre de référence

C'est un jeu de barre générateur où le module et la phase de tension (V, è) sont tout deux spécifiés. Les puissances (P, Q) sont inconnues et doivent êtres calculées en dernier.

Le jeu de barre de référence, est choisi parmi les jeux de barres générateurs dont la puissance active est la plus importante. Ce jeu de barre est pris comme référence des angles de tension.

b) Jeu de barre contrôle

Ce jeu de barre est connecté à un générateur délivrant une puissance active P sous une tension constante V contrôlée par un régulateur automatique de tension (AVR). Donc (P, V) sont spécifiées alors que (Q, è) sont à calculer.

c) Jeu de barre de charge

Ce jeu de barre alimente une charge caractérisée par sa puissance active P et réactive Q. Donc, (P, Q) sont spécifiées, alors que (V, è) sont à calculer [05].

I-4 Les équations de l'écoulement de puissance

I-4.1 Les équations aux J.d.B de charge

Les puissances active et réactive à chaque J.d.B « i » sont :

P i - jQ i = V i *. I i (I-1)

P jQ - Avec : * i i I = ^i V i

(I-2)

I y V y V V y y V y V

= . 1 ( 1

+ - + +

2 ) ( ) 1 - . (I-4-1)

1 p s p s s 1

Dans la formulation de l'équation du réseau, si les éléments shunts de mise à la terre sont inclus dans la matrice des paramètres l'équation (I-2) donne le courant total au J.d.B. D'un autre coté, si les éléments shunts du réseau ne sont pas inclus. Le courant total au J.d.B « i » est :

(I^-3)

P jQ

i - i

I = - Y V

.

i * i i

V i

Y_i : Admittance totale shunt au J.d.B « i ».

Y_i. V_i : Courant de shunt circulant du J.d.B « i » vers la terre [06].

I-4.2 Exemple d'un système à deux J.d.B

2

dB JdB

FigureI-4 : système à deux J.d.B

On note que:

- S 1 = S G 1 - S_D1 , S 2 = S _G2 S D 2

Et en générale :

S i= S_Gi - S_Di (I-4)

SP jQ = + i i i

( P Gi jQGi ) (P Di + jQDi)

S i ( P _Gi P _Di) + j(Q Gi jQDi)

L'application des lois de KIRCHHOFF sur le système donne : Au niveau de J.d.B « 1 »

*

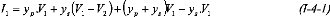
SOn sait que : S = V I * 1

1 . 1 I =

1 ¹ V *

1

Au niveau de J.d.B « 2 »

I y V y V V y y V y V

= . 2 ( 2

+ - + +

1 ) ( ) 2 - . (I-4-2)

2 p s p s s 1

*

2

Avec :

S 2 = V₂ . I 2 I₂ =*

^SV₂

Alors on peut écrire (I-4-1) (I-4-2) sous la forme :

I1 =Y11 . V	+ Y12		. V2		(I-5)
I 2 Y21 . V1		+ Y22		. V2

Avec Y 11 = y _p + y_s ,Y 22 = y _p + y_s

Y 12 = - ys			,Y = - y 21 s
Ybus	=	Y Y 11 12 Y 21 Y22		(I-6)

[[

On remplace (I-5) en (I-6) : I 1 -1 LI 2 _1] = Y ₁₁ Y 12 1 V1

Y ₂₁ Y 22 _J V2

Et ainsi de suite. On peut généraliser la méthode de formulation comme suit pour le système à « n » J.d.B connectés entre eux

_[m

I 1 = E y 1 i V₁ +

i = 1,i ?n

( - y₁₂ )V ₂ + ..............+ ( _-y1n ) V_n

. . . .

m

I n = ( -y n 1 ) V ₁ + ( - y 2 n )V+ + [ y ni )Vn

2

i i n

= ?

1,

La matrice admittance est donc :

n

i = 1,i ?n

y . . 1 i

( -y1n )

. . . .

Ybus

=

. .

z

( )

- y n 1

m

yni

i = 1,i ?n

. . . .

I1 I2				V 1 V2
Ibus	=	.	Vbus		=	.
. I n				. Vn

I-4.3 Calcul de la puissance au niveau de J.d.B On a :

S P P j Q jQ P jQ

i ( Gi

= - +

Di ) ( Gi - Di ) i

= + i

Alors :

Si^*= Pi + jQi = Vi ^*.Ii

n

S V y V

* *

= . . (I-7)

(I-8)

i i ij j

1

j

=

1

j

Donc

cos

( ä_j - ä + ãij

sin

V_j

En coordonnées polaires :

V _i= V _i. ä_i

yij

yij

. ãij

(ä ä ã - + ) j i ij

V i

P i

V_j

yij

V i

Qi

yij

SP jQ V y V

* *

= - = .

i i i i ijj

j( ä _j -ä i +ãij)

=

e

y ij

V_j

V i

I-4-4 Les équations d'écoulement dans les lignes

Quand la solution itérative des tensions aux J.d.B est achevée, on peut calculer l'écoulement dans les lignes.

Le courant au J.d.B « i » dans la ligne de connexion de noeud « i » vers le noeud « k » est :

'

(I-9)

I ik ( V i - V k ) y + V . yik

ik i

2

y_ik : Admittance de la ligne entre les J.d.B « i » et « k ».

y_ik : Admittance totale de la ligne de charge.

'

'

V . y2 : Contribution du courant au J.d.B « i » due a la ligne de charge.

La puissance écoule, active et réactive, est :

V* I

Pik - iki .ik (I-10)

'

y

P - jQ = V V - V y + V V (I-11)

* ( ) *. . 2 ^ik

ik ik i i k ik i i

Soient Pki et Qki les puissances active et réactive reparties du J.d.B « k » vers le J.d.B « i ».

'

P - jQ = V V - V y + V V (I-12)

* ( ) *. . y 2 ^ik

ki ki k k i ik k k

Les pertes de puissances dans la ligne « i-k » sont égales à la somme algébrique de la répartition des puissances déterminée a partir des relations (I-11) et (I-12).

I-4-5 Les pertes de puissance dans lignes

Au niveau de J.d.B la puissance apparente écoule est la différance entre la puissance générée et la puissance demandée.

Pour un J.d.B « i » :

On a : S_i = S Gi - SDi

Avec :

P i = P Gi - Di= Fip

Q Q Q F

= - =

i Gi Di iq

P= F =ipEP Gi - EPDi

Q_i = Fiq = QGi - Q Di (I-13)

Le système d'équations (I-13) exprime l'expression des pertes.

Ou bien on peut calculer les pertes par une autre méthode, on calcule les pertes au niveau des lignes puis la somme algébrique donne l'expression des pertes [06]

P P P = + Lij ij ji aij = Qj + Qji

(I-14)

I-5 Résolution des équations de l'écoulement de puissance

Il existe deux méthodes de base pour la résolution des équations non linéaires de l'écoulement de puissance : Gauss-Seidel (GS) et Newton-Raphson (NR). La méthode la plus utilisée est celle de NR à cause de sa convergence quadratique [02].

I-5.1 Méthode de Newton-Raphson

La méthode de NR, nous permet de remplacer le système d'équations non - linéaires, par un système linéaire.

Soit f( x ₁ , x ₂, x_n ) une fonction à (n)variables. Le développement de cette fonction en série de

Taylor, au voisinage d'un point( a ₁ , a ₂, a_n ) , nous donne [05]

a_n

? f ? f ? f

f x x x f a a a x a

( ) (

) ( )

+ - ( )

x a .... ( )

1 2

, ,.... x a

n 1 2

, ,.... + + -

+ -

n 1 1 2 2 n n

? x ? x

? x

1 a 2 a n

^{1 2}

Si on pose, Äx i = x_i - a _i ( i = 1,2, ...n)

on aura

a_n

? f ? f ? f

f x x x f a a a

( ) (

- )

1 2

, ,.... + Ä x

n 1 2

, ,.... = Ä x + + Ä

x ....

n 1 2 n

? x ? x ? x

1 a 2 2

a n

¹

Considérons maintenant un système d'équations non - linéaires, à n variables

f1 f2 fn

(((x x x , ,... ) = 1 2 n x x x , ,... ) = 1 2 n x x x , ,... ) = 1 2 n

y 1 y 2 y n

(I-15)

Où,

f _k ( x ₁ , x ₂ ,... x _n ) = y _k , k = 1,2, n

Le développement en série de Taylor, du système d'équations (I-15), au voisinage d'une

estimation initiale( ⁰ )

x_k , donne

? f ? f

f x x x y f x x x

0 0 0 0

( ) (

= = ) x ⁰ x (I-16)

1 2

, ,.... , ,.... + + Ä

+ Ä ....

k n k 1 2 n 1 n

? x ? x

x_n⁰

1 x 0 n

1

k = 1,2, n

Äx_k , représente la correction à ajouter à ⁰

x_k , pour se rapprocher de la solution correcte.

Le système (I-16), peut être écrit sous la forme matricielle suivante

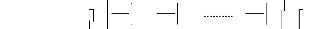
f 1

y₁

-

( )

⁰ x ⁰

x , ,

1 n

? f 1

? f 1

? f 1

0

Ä x

1

X 0

1

X 0

n

X 0

2

n

?x₁

? x

? x

2

(I-17)

-

n n

0

( x ⁰

x , ,

1 n

y f

0

? f_n

? f n

? f n

Ä x

n

X 0

1

X 0

n

X 0

2

2

?x

? x

? x

1

n

Ou encore

[ Ä U ] 0 = [ J ] ⁰ . [ Ä X ]⁰ (I-18)

[ J] est la matrice jacobéenne du système (I-15). d'où l'on tire

[ ] ( [ ] ) [ ]0

Ä X 0 = J 0 - . Ä U (I-19)

1

La première solution approchée du processus itératif est calculée par [ X ] 1 = [ X] ⁰ + [ ÄX]⁰

Généralement, pour une itération (k), On a

[ X ] K = [ X ] ^K + [ ÄX ]K

⁺¹ (I-20)

I-5.2 Application de la méthode de Newton-Raphson, au problème de l'écoulement

de puissance

Mathématiquement, le problème de l'écoulement de puissance peut être réduit à un ensemble d'équations non-linéaires où le module et l'angle des tensions aux niveaux des jeux de barres sont les variables. Dans la forme la plus compacte, le nombre d'équations vaut approximativement deux fois le nombre de jeux de barres. Les non-linéarités peuvent être approximativement classées sous une forme quadratique. La technique de N-R basée sur le calcul du gradient et de la relaxation est utilisée comme méthodes de solution pour ces systèmes d'équations.

Le problème peut être résolu en utilisant soit les coordonnées rectangulaires soit les coordonnées polaires. Il est préférable d'utiliser la forme polaire pour faire apparaître les différentes grandeurs qui caractérisent le réseau électrique.

D'après la forme générale d'équations de puissance au J.d.B :

n P= i

y ij

V i

V j

cos(ä ä ã ) j i - + ij

Fip

j 1

n

i = 1,2, ,n (I-21)

Q_i

V i

V j

y ij

Fiq

sin(ä ä ã )

j i

- + ij

j 1

Où i = 1 c'est le J.d.B de référence

n : Nombre de J.d.B i : Numéro de J.d.B Après développement de _Fip ^et _Fiq en série de TAYLOR autour de la première approximation :

? F ? F ? F

(0) (0) (0) (0) (0) (0) (0)

= ( )

^ip ( )

^ip Ä + ( )

ip

P F + Ä +

ä + ä Ä V

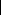
i ip 2 n 2

? ä ? ä ? V

(I-22) )

2 n 2

? F ? F ? F

(0) iq (0) (0) (0) (0) (0) (0)

( ) Ä + ( )

^iq Ä + ( )

iq

Q F

= + ä + ä Ä V

i iq 2 n 2

? ä ? ä ? V

2 n 2

Ave ⁽⁰⁾

Fip et ⁽⁰⁾

Fiq ) sont des fonctions de tension et de phase :

ÄPP

A partir de la relation de Ä QQ

Avec c

P P F (0) (0) Ä = - i i ip(I-23) Q Q F (0) (0) Ä = - i i iq )

Les deux systèmesd'équationss(IV-2)) et(IV-3))donnentt :

? F _{2 2p p}? F _{2 2p} p?F _{2 2p} p?F22P 2 ⁽⁰⁾⁾¹? ä ₂ 2?ä n nV 2 ₂VV n

ÄA

p

ä (0) Ä 2 )

F₌

Ä P(0))? F F? F F?F F?F n

np np np np

^ÄA änn( 0))

? ä _{2 2}?ä_n nV ₂ 2Vnn

.

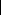
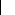
?a F _{2 2q q}? F 2 q ^q?F 2 q q?F22 _q

? ä _{2 2}?ä_n nV 2 2Vnn

ÄA Q ⁽⁰⁾⁾²

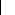
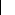
ÄAV2(0))

.

(0) ?a F nq _q? F nq q?Fnqq ?Fnqq

ÄA Q

ÄA Vnn (0)

_n ?a

ä 2 2?änn

V 2 2Vnn

Donc on peut écrire le système comme suit :

Ää⁽⁰⁾⁾ ₁ IJ(0))--11 ÄP(0))?>(0) (0)

Ä V Ä Q )

(I-24))

ÄA

ÄPP

(0)₌

(0)]Ää(0)m

On rappel que :

( K ) ( K 1)

+

Ä = ( K )

ä i ä i -

ä i

( k) ( K+1 ) (K)= V i - V i

V i

ÄA

i ?# 1( ref ), ii ?# 2(cont)(I-25))

V i

yij

cos(ä_j - ä _i + ãij)

, i ? j

V_j

n

+

j = 1, i ?j

yij

yij

cos( ã_ij )

Sous matrice J2:

Sous matrice J3:

Sous matrice J4:

sin(ä j - ä _i + ã_ii )

, i = j

?Pi = 2 V i

V_i

?

Q i = V i

cos(ä_j - ä + ã_i, )

, i ? j

?

? ä_i

cos(ä ä ã

- + ) j i ij

, i = j

yij

V_j

yij

V_j

n

? Q_i

V i

?

yij

V_j

ä i

j = 1, i ?j

?P_i

?

ä i

?P_i

?

V i

n

V_j

V i

yij

j = 1, i ?j

cos(ä - ä i+ ãij)

,i = j

sin(ä j - ä _i + ij

, i ? j

sin( ä- ä + ã _ii) - 2

sin( ãij)

, i = j

? Q_i

?

yij

V_j

V i

n

?

? Q_i

yij

V_j

V i

j = 1, i ?j

(I-27)

(I-29)

(I-31)

L'adaptation de (I-24) avec (I-25) donne :

( 1)

+ ä ( )

ä K ^K Ä ä

i = +

V ^K

( 1)

+ V ^K

( )

Ä V

D'une manière générale

? [ä _i ( K + 1) [_ä( K )

-1 Ap(k)

V ( K + 1)=

V ( K ) L

#177; L_J u()

V

- Ä)k

_[

ÄP] ÄQ = [ J ] ÄV

J=

J 1 J2 J 3 J4

J₁ , J₂ , J₃ , J₄ Sont les sous matrice de Jacobienne.

I-5.3 Détermination des sous matrices de la Jacobienne J :

A partir du système d'équations (IV-1) on peut déterminer les éléments de J [05]. Sous matrice J1:

? ä i

?P_i

V i

V_j

yij

sin(ä j - ä _i + ij

, i ? j

(I-26)

I-5.4 Remarques

· Si les écarts de puissance réactive au niveau des jeux de barres de génération ne sont pas donnés, les lignes et les colonnes correspondant à ces jeux de barres doivent être éliminées.

· Si la puissance réactive générée au niveau d'un jeu de barre de génération dépasse sa limite inférieure ou supérieure, ce jeu de barre sera considéré comme un jeu de barre de charge avec Q_g = Q_min ou Q_g = Qmax et le module de la tension (V) devient une inconnue à calculer [02].

I-6 Algorithme de Newton-Raphson

Début

Lecture des données du système

Formulation de la matrice admittance Yb_us

Estimation initiale des tensions et de phase au .d.B
V.(0) ₈( k) i= 1,2, ,n i ? ref

Mettre le nombre d'itération k=1

Calcul des puissances active et réactive aux J.d.B
P ( k ) = ( P 1 ( k) P ₂( k ) P ^{n( k)});i ? ref

ak )= ( 0⁰, , Q _n( k ) ); i ? ref

Détermination de maximum variation dans la
puissance

max ÄP Et max ÄQ

Calcul des différences entre les puissances
estimées et les puissances calculées

Si

max ÄP ( k) =

Oui

Calcul les puissances des lignes et les valeurs des
tensions aux J.d.B

Fin

Non

Calcul des éléments de la matrice Jacobienne

Calcul des corrections de tension et de phase Jacobienne

Calcul des nouvelles tensions aux J.d.B

ä i ( k ) paräi( ^k+1)

( k) par V,. ( k+1)

Remplacer Et

i = 1,2, ,n i ? ref

K=k+1

Figure I-5 : Organigramme simplifié de l'algorithme de Newton-Raphson

I-10 Application Newton-Raphson à un réseau de six JDB

Ce réseau est constitué de 11 lignes de transport, 3 générateurs et 3 charges au niveau des jeux de barres n° 4, 5 et 6 Figure (I-6). La puissance et la tension de base sont respectivement, 100 MVA et 230 KV. Les données de ce réseau sont montrées dans l'annexe.

Les puissances actives et réactives générées en MW et MVAR respectivement [02]. Le niveau de tension de chaque jeu de barre i en p.u doit obéir à la contrainte suivante

0 .90 = V_i = 1. 1 0

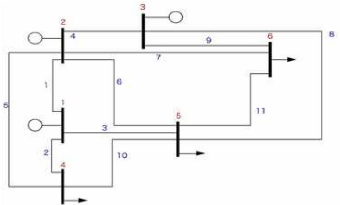
Figure I-6 : Schéma unifilaire du réseau électrique à 6 jeux de barres.

JdB N°		Tension	Puissance générée		Puissance générée
	Module	Argument	Mw	Mvar	Mw	Mvar
1	1.0500	0.0000	107.8755	15.9562	0.0000	0.0000
2	1.0500	-3.6712	50.0000	74.3565	0.0000	0.0000
3	1.0700	-4.1958	60.0000	89.6268	0.0000	0.0000
4	0.9894	-4.1958	0.0000	0.0000	70.0000	70.0000
5	0.9854	-5.2764	0.0000	0.0000	70.0000	70.0000
6	1.0044	-5.9475	0.0000	0.0000	70.0000	70.0000

Tableau I-1 : Tension et puissance au niveau de J.D.B.

Branche N°		Puissances transmises				Pertes
AU	DU	P(I J)	Q(I J)	P(J I)	Q(J I)	PL	QL
1	2	28.690	-15.419	-27.785	12.819	0.905	-2.600
1	4	43.585	20.120	-42.497	-19.933	1.088	0.188
1	5	35.601	11.255	-34.527	-13.450	1.074	-2.195
2	3	2.930	-12.269	-2.890	5.728	0.040	-6.541
2	4	33.091	46.054	-31.586	-45.125	1.505	0.929
2	5	15.515	15.353	-15.017	-18.007	0.498	-2.653
2	6	26.249	12.399	-25.666	-16.011	0.583	-3.612
3	5	19.117	23.174	-18.023	-26.095	1.094	-2.921
3	6	43.773	60.724	-42.770	-57.861	1.003	2.863
4	5	1.083	-4.942	-4.047	-2.785	0.036	-7.727
5	6	1.614	-9.663	-1.565	3.872	0.050	-5.791

Tableau I-2 : Puissances transmises et pertes dans les lignes

La puissance active générée Totale (MW) est :	217.8755
La puissance réactive générée Totale (MVAR) est :	179.9395
La Puissance active demandée Totale (MW) es t:	210.0000
La puissance réactive demandée Totale (MVAR) est:	210.0000
Les Pertes Actives Totale (MW) est :	7.8755
Les Pertes Réactives Totale (MVAR) est :	-30.0605
Le Facteur de Puissance est :	0.7710

Tableau I-3 : Résume la solution obtenue par N-R

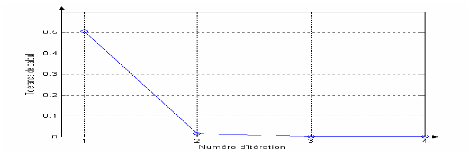
Figure I-7 : Convergence de l'algorithme N-R pour le réseau électrique à 6 JDB.

I-11 Influence d'une consommation excessive de réactif au bus 6

Si nous augmentons progressivement la charge connectée au bus 6, la chute de tension en ce noeud varie de la façon décrite sur la figure (I-8) suivante.

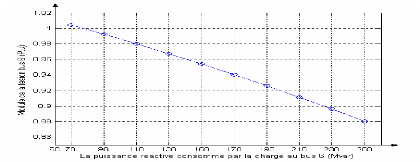
Figure I-8 : Chute de tension sur le J.B 6

Le résultat obtenu sur cette la figure II.9 confirme bien la théorie selon laquelle : l'absorption de puissance réactive en un noeud à pour effet de diminuer la tension en ce noeud.

Il faut savoir qu'une diminution de la tension en un noeud peut entraîner la diminution des tensions des noeuds voisins. Cette réduction excessive de la tension peut occasionner une instabilité de tension et provoquer le black-out local plus général [05].

I-12 But du banc de capacités

Si nous augmentons la puissance des charges inductives pour différentes valeurs de la puissance réactive des bancs de capacités, nous obtenons la figure (I-9).

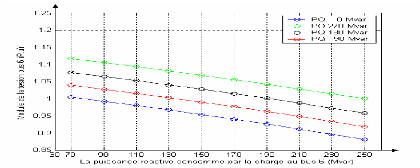
Figure I-9 : Influence de la compensation la tension

La théorie est bien en accord avec les résultats obtenus avec le logiciel de calcul du load flow. Pour des charges fortement inductives, il faut injecter de la puissance réactive pour soutenir la tension. Cette puissance doit pouvoir être régulée car, pour des injections importantes (270 MVAr), la tension du jeu de barre 6 est prohibitive (1,0044 pu).

En pratique, nous aurons recours à des systèmes faisant intervenir des TCR (thyristor controlled reactor), des TSC (thyristor switched capacitor) et bien d'autres. En effet, une charge est fluctuante et il ne faut pas transformer le problème local en surtension en cas déconnexion de la charge [08] [05].

I-13 Conclusion

Dans ce chapitre, on a fait la modélisation de quelques éléments de puissance constituants le réseau de transport et dont leur modélisation entre directement dans le calcul de l'écoulement de puissance. Le problème de l'écoulement de la puissance peut être donc résolu par la technique de NR qui converge avec une même vitesse, mesurée par le nombre d'itérations, pour les larges et courts systèmes, en moins de 4 à 5 itérations en général. Le problème le plus important dans l'industrie d'électricité est de réduire au maximum le coût de la production de l'énergie électrique générée par l'ensemble des centrales interconnectées. Ce problème ne peut être résolu par l'écoulement de puissance mais par l'optimisation de l'écoulement de puissance. Ce dernier problème est le sujet du deuxième chapitre.

CHAPITRE II

Dispatching Economique

II- Dispatching Economique

II-1 Introduction

Le calcul de l'écoulement de puissance conventionnel ne répond que partiellement à un problème plus général comportant une exigence d'optimisation, par exemple assurer une alimentation correcte de la clientèle et une bonne répartition de la puissance. En minimisant les coûts de production par des centrales qui ont chacune un coût marginal particulier, fonction de la puissance fournie, ou en optimisant le plan de tension de façon à respecter les contraintes sur les matériels, à éviter les risques d'instabilité de tension, à minimiser les pertes joule ou les moyens de compensation réactive. Dans les études d'exploitation et de planification des réseaux électriques, on est amené à résoudre des problèmes d'optimisation consistant à minimiser une fonction des variables P, Q, V, et 0, et des contraintes d'inégalité qui traduisent les limites de fonctionnement des ouvrages (groupes de production, lignes, transformateurs, ...etc.). Ce type de problèmes est connu par le Dispatching Economique ou plus généralement : Ecoulement de Puissance Optimal.

En doit déterminer la contribution de chaque centrale électrique en service pour satisfaire la demande des consommateurs en énergie électrique de sorte que le coût de production de l'énergie totale soit le moins cher possible.

Normalement la capacité de génération est plus grande que la demande de la charge électrique, c.-à-d., les générateurs interconnectés doivent être capables de produire une puissance électrique plus grande que celle consommée par les clients. Il faut savoir que, en réalité, les centrales ne sont pas situées à la même distance du centre de la charge, ces centrales sont reliées entre eux par des lignes de transmission.

Afin de déterminer la répartition économique de la charge entre les générateurs interconnectés, le coût de fonctionnement de ces centrales doit être exprimé en fonction de la puissance à la sortie (débit). La fonction du coût à une forme non linéaire qui peut approximer une courbe quadratique. A chaque étape, la condition de fonctionnement de chaque générateur est vérifiée pour l'assurer dans sa plage de fonctionnement. En particulier il faut vérifier les angles de phase et les tensions au niveau des jeux de barres aussi bien que les limites de charge de la ligne.

Le but de ce chapitre est de montrer comment on peut résoudre le problème de la répartition des puissances sur les centrales électriques avec un coût de production minimal [09].

II-2 Architecture des réseaux électriques

Le réseau à très haute tension THT (400 KV, 225KV) d'interconnexion internationale forme un ensemble maillé sur lequel sont raccordées les grandes centrales (centrales nucléaires de 1000 MW, par exemple). Il est complété par le réseau de répartition (60 à 150 KV) souvent exploité en poches reliées au niveau supérieur de tension et sur lequel se raccordent des centrales électriques de moindre puissances, ainsi que les grands utilisateurs industriels. On trouve en suite un réseau de distribution (de 20 KV à 400 V) desservant la clientèle (petites et moyennes entreprises, commerces, secteur résidentiel). Ce réseau de distribution est généralement de structure radiale, éventuellement bouclé dans des zones urbaines pour assurer la continuité de service, voire bouclé même en basse tension dans certaines grandes villes. Le coût d'un réseau bouclé est plus élevé par la complexité du contrôle et de la protection, mais ce type de réseau se caractérise par une meilleure continuité de service.

L'alimentation d'une grande agglomération se fait en général par une boucle à 380 ou 225 KV, alimentée par le réseau d'interconnexion et sur laquelle sont raccordés des postes abaisseurs vers le réseau de répartition, souvent en câble pour la pénétration urbaine. Sur ce réseau de répartition sont branchés des postes abaisseurs vers le réseau de distribution (15 à 20 KV), bouclé et enfin le réseau basse tension de structure radiale alimentant les consommateurs (en triphasé ou en monophasé) [04].

II.3 Stratégie du fonctionnement des Centrales électriques

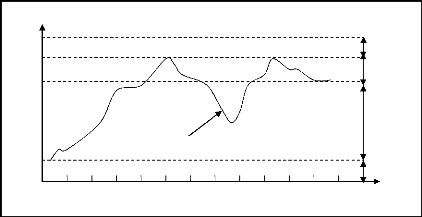
Il existe un nombre infini des formes de fonctionnement pour assure un chargement précis d'un système. On distingue chacune des unités de génération en désignant les puissances spécifiques de chacune d'elles en Mw ou Mvar. La figure II-1 illustre comment fonctionne à 100% de leurs capacités pendant 24 heures supportent la charge de base.

Des générateur intermédiaires commandés fonctionnent la plupart du temps mais pas nécessairement sous une charge totale. On procède au couplage des unités des pointes à la ligne pendant des heures chaque jour. On a besoin d'une capacité de réserve pour affronter le cas d'urgences.

P (Mw)

Charge de pointe

2 4 6 8 10 12 14 16 18 20 22

Demande total de
système

Capacité de réserve

Charge 'intermédiaire

Charge de base

Heure

Figure II-1 : stratégie de fonctionnement des centrales suivant la demande de puissance électrique

II-3.1 Unités de charge de base

Les unités nucléaires sont généralement rangées dans cette catégorie a cause du besoin de conservation de l'équilibre thermique entre le réacteur atomique et le générateur de vapeur, il est préférable de stabilise les puissance actives délivrées pour ce genre d'unités a un niveau constant dans la mesure du possible, et faire fonctionner les unités dans des valeurs constantes de puissance. II-3.2 Unités intermédiaires

Quand il faut organiser les puissances actives délivrées, on préfère utilise les unités fonctionnant hydrauliquement, car on contrôle l'énergie générée par celle-ci en jouant sur le débit d'eau entrant à la turbine.

Les centrales électriques ne sont pas toutes hydrauliques, mais on utilise des centrales thermiques contrôlables. À cause des constantes de temps thermique d'un système à vapeur, il est toujours nécessaire d'organise ces centrales dans les limites de leurs moyennes maximales. C'est-àdire la moyenne où l'on peut varier le niveau d'énergie ou puissance en Mw par minute.

II-3.3 Unités de pointe :

Les générateurs entraînés par des turbines à gaz peuvent répondre à l'augmentation de la charge avec une grande vitesse. Pour cela, ils sont utilisés fréquemment pour les heures de pointes, mais lorsqu'on dispose des générateurs entraînés hydrauliquement ceux-ci sont préférés en premier lieu. Les centrales de pointe doivent être mises en marche dans un délai très court, elles utilisent donc des moteurs à diesel, des turbines à gaz, des moteurs a air comprimé ou des turbines hydrauliques à réserve pompée.

Remarquons que la période d'amorçage est de 4 à 8 heures pour les centrales thermiques et de quelques jours pour les centrales nucléaires. Il n'est donc pas économique d'utiliser ces centrales pour fournir la puissance de pointe [10] [09].

II-3.4 Unités de réserve :

La gamme des générateurs demandés peut être constituée de générateurs conservés à la sortie partielle (capacité de réserve) ou des générateurs intermédiaires à des degrés différents de disposition. Le coût d'énergie varie en grande partie en fonction du dollar par Mw heures ($/Mwh) entre les différentes unités précédentes. L'unité de pointe est considérée la plus chère, car elle n'est pas exploitée toujours et on peut s'abstenir d'acheter ce type d'unités pour des années en minimisant le pie de demande par le contrôle de la charge. Il est primordial pour n'importe qu'elle entreprise de production d'énergie électrique de conserver les unités mixtes convenables et cela ne soit pas due seulement à la variation de l'énergie demandée par heure, mais il est obligatoire de procéder régulièrement à la maintenance de toutes les centrales électriques [11].

En ce qui concerne les centrales nucléaires, il fait les alimenter en combustible. La réussite de l' unité productrice d'énergie à gérer les différentes unités dépend essentiellement de sa capacité à réaliser le compromis entre la génération de l'énergie et la demande de la charge non pas pour 24 heures mais pour des années entières [09].

II.4 Dispatching Economique :

Dans le dispatching économique, la fonction objective à minimiser est le coût total de production des groupes thermiques, de telle sorte que la charge électrique du système soit entièrement satisfaite. Dans ce cas, la seule contrainte est que la somme de toutes les puissances actives générées, soit égale à la charge totale du système.

On en conclut que le modèle utilisé par le dispatching économique standard, considère que les pertes de puissances actives dans les lignes de transport et les transformateurs sont négligeables, et que les équations de l'écoulement de puissance ne sont pas prises en considération.

Le système électrique est alors équivalent à un seul jeu de barre où sont connectées tous les générateurs de puissance et toutes les charges électriques Figure II-2.

Le coût de l'énergie à l'entrée du générateur, est évalué en (Mbtu/h) ou ($/MW), qui représente la quantité de fuel ou de combustible nécessaire pour le fonctionnement de la chaudière.

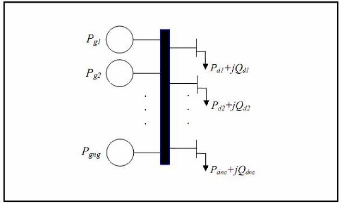
Figure II-2 : Modèle du système électrique utilisé dans le Dispatching Economique.

Le coût de production à l'entrée $ / Mw varie avec la puissance à la sortie du générateur P_gi en

Mw. La relation entre le coût de production et la puissance de sortie est appelée << courbe de coût >> C _i ( P _gi ) , Figure II-03.

Figure II-3 : Courbe de coût typique (entrée-sortie) d'un générateur
La fonction du coût d'un générateur i, peut être approximée par une forme quadratique, comme suit

( ) i . P gi [ $ / h]

2

C _i P gi = i + _i . P _gi +

ng Sujet à la contrainte ?= P gi = i 1

P d

(II-02)

Où _i , _i , _i sont des coefficients constants propres au générateur i.

La dérivée de la fonction de coût par rapport à la puissance générée, représente l'accroissement du coût de combustible Figure II-04.

dC

i = + 2 . [ $ / Mwh]

dP gi

i i gi

P

La courbe de l'accroissement du coût de combustible, mesure le coût additionnel du combustible $ / Mw , pour augmenter la puissance de sortie du générateur de 1 Mw [02].

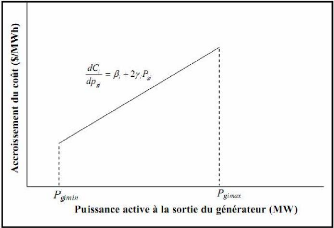
Figure II-4 : Courbe typique de l'accroissement du coût de combustible

II.5 Formulation mathématique du problème du Dispatching Economique :

Le problème du dispatching économique consiste à minimiser le coût total du combustible (C), sujet à une seule contrainte d'égalité qui est la somme de toute les puissances générées est égale à la puissance totale demandée (Pd).

Mathématiquement on peut écrire

ng ng

Minimiser ? ( ) ? (

C = C P = + . + . (II-01)

P ² )

i gi i i gi

P i gi

i = 1 i = 1

Dans la pratique, chaque puissance générée ( P_gi ) est limitée par une limite inférieure ( Pgi min ) et une autre supérieure( Pgi max ) , ce qui donne la contrainte d'inégalité suivante

P gi min = P gi = P gi max i=1,2,...,ng (II-03)

II.5.1 La méthode Lambda :

Le problème d'optimisation devient comme suit :

ng

Minimise : ?

F = F _i P gi

( )

i=1

ng A condition que : 0 H = ?= - = P gi P d i 1

(II-04)

Le système de équation (II-04) est un problème d'optimisation non linéaire avec contraintes, qui doit résoudre par le développement d'une fonction s'appelle la fonction de Lagrange.

Pour obtenir l'extremum d'une fonction objective, on doit ajouter la fonction de contrainte à la fonction objective, par la multiplicateur de Lagrange, qui préalablement indéterminé.

La fonction augmentée de Lagrange du problème est donnée par :

L = F + . H

La condition nécessaire pour avoir l'optimum est quand les dérivée premières de la fonction de Lagrange par rapport aux P_gi et sont égales à zéro.

Dans ce cas on a ng+1 variables, les inconnues sont les puissances générées et le multiplicateur de Lagrange.

La dérivée de la fonction de Lagrange par rapport à ne donne que la contrainte d'égalité. D'une autre façon, les puissances générées P_gi optimales sont obtenues quand les dérivées de la fonction

du coût par rapport aux puissances générées soient égales à zéro, en respectant que leurs sommes soit égale à la puissance demandée totale.

On obtient l'équation suivante des dérivées :

?L ?Fi	0
?Pgi P ? gi

F

Donc : i

i

? = = IC

?Pgi

IC_i: S'appelle l'incrément du coût

Donc, la condition d'existence d'un optimum pour la fonction de coût des centrales électrique thermique, et que l'incrément du coût IC_i , soit égale pour chaque générateur, une même valeur,

préalablement indéterminée qui est .

Et bien, pour cette condition on doit ajoute une contrainte d'égalité, la somme des puissances générées égale la puissance demandée total.

La contrainte d'inégalité est que les puissances générées ne dépassent pas ses limites. On résume le problème comme suit :

? F i
? P gi

ng équations.

P g min = P gi = P g max ng inégalités. (II-05)

ng

?= Pgi = i 1

P d

Une équation.

Pour le problème des violations des contraintes d'inégalités, on peut augmenter le système des équations (II-05) par l'ensemble d'équations :

? F i
? P gi

? F i
? P gi

? F i
? P gi

Pour P g min = P gi = Pgmax

= Pour P_gi = Pg max

= Pour P_gi = Pg min

Si certains générateurs dépassent sa limite, on prend cette limite, et on continue le processus de calcul pour les autres.

La valeur de lambda initiale doit être comprise entre _min et _max correspondants respectivement

aux Pg min et Pg max

- L'algorithme de la méthode lambda :

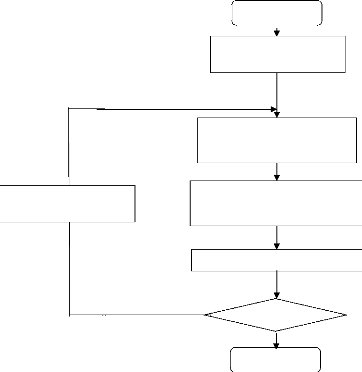
Donner à une valeur
initiale

Non

Oui

Imprimer

Calcule nouvelle valeur
de lambda

Si P gi = P g min pose P gi = P g min
Si P gi = P g max pose P gi = P g max

Calcule les puissances
générées P_gi pour i=1,2...ng

Critère d'arrêt atteint

Calcule å =Ó pgi-Pd

Début

Figure II- 5 : Organigramme de la méthode lambda

II.5.2 Solution du problème du Dispatching Economique sans pertes

Pour résoudre le problème du dispatching économique, on fait appel à la fonction de Lagrange, formulée comme suit

? ng ( ) ?

? - ?

ng

2

+

L = . + . + ? = ?

P (II-06)

i i gi

P i gi

P P d gi

i = 1 ? i 1 ?

Est le multiplicateur de Lagrange. Les conditions nécessaires pour un minimum sont données par

? L = . + 2 . - = 0 (II-07)

i i gi

? P gi

P

ng

L = -

P d P gi = 0 i 1,2,..., ng

=

(II-08)

? ?=

? i 1

P gi min = P gi = P g i max

Donc, pour un fonctionnement optimal des générateurs, il faut que le l'accroissement du coût de tout les générateurs soit le même, c-a-d égal à( ) .

Le système d'équations (II-08) comporte (ng + 1) équations avec (ng + 1) inconnus, qui peuvent

êtres résolues par la substitution des valeurs de ( P_gi ) des premières équations dans l'avant dernière

-

i

i

P gi

2

=

ng

-

?=

i 1

i

P d

=

2 i

i 1,2,..., ng

=

(II-09)

La valeur optimale de ( ) est alors calculée comme suit

ng

*

P_d +

i

i

? 2 1

=	=				(II-10)
		ng ?	1
		1		i

La valeur optimale * est remplacée dans les premières équations de (II-09) pour obtenir la puissance optimale à générer par chaque générateur

Pgi

2

? ? 1 ? ? i ? ?

P d

ng

?

+ ?

i ?

2

1 ?

i - (II-11)

ng

?

1

i ?

1 ?

i ?

II.5.3 Solution du problème Dispatching Economique avec considération des pertes

Dans les systèmes réels, le transport de l'énergie électrique vers les jeux de barre de charge est souvent accompagné par des pertes de transmission. Le problème du dispatching économique devient un peu compliqué par rapport au cas précédent où les pertes ont été négligées.

Dans ce cas, la contrainte d'égalité représentée par l'équation d'équilibre de puissance donnée dans (2.3) doit inclure ces pertes. Si on désigne par PL les pertes totales de puissances actives, la contrainte d'égalité devient

ng

? P gi = P _d + P (II-12)

L

i=1

Le lagrangien est alors formulé par

? ? (II-13)

?

ng ng

?

L = ? ( + . P + . P ² ) + ? P P

+ - ? P

i= 1 ? i= 1

i i gi i gi d L gi

Les conditions nécessaires pour un minimum sont données par

0

? L ? ? P ?

L

= +

. 2 . P - -

?? 1 ??

i i gi

? P ? P

gi ? gi ?

ng ? L = + - P d P L ?= P gi ? i 1

0

i 1,2,..., ng =

(II-14)

P gi min = P gi = P g i max

Les pertes de puissances actives dans le système électrique, P_L sont fonctions des impédances du réseau et des courants qui transitent dans les différentes branches du système électrique [4].

On peut donc considérer que les courants sont fonction des variables indépendantes, P_gi et p_d .

La première équation de l'expression II-14, nous donne une relation directe entre la puissance générée ( P_gi ) et le multiplicateur de Lagrange( ) , donnée par

dC

i

i

dP

gi

(II-15)

dC

=

=

.

?P_L

1

L i

gi

dP

? Pgi

1

Le terme =

L =

1

i ? P L

est appelé : facteur de pénalité du générateur i.

? P gi

Remarques

Il existe trois approches générales pour résoudre le problème du dispatching économique avec pertes de puissance

1. La première approche consiste à considérer les pertes de puissances actives constantes, dans la contrainte d'égalité donnée par l'équation (II-12).

2. La deuxième approche consiste à développer une expression mathématique des pertes de puissances actives, en fonction des puissances actives des générateurs. Celle-ci est connue par la méthode de « formule des pertes », ou méthode des « coefficients B »

3. La troisième approche consiste à introduire les équations de l'écoulement de puissance comme contraintes essentielles dans la formulation du problème d'optimisation. Cette approche est connue par l'Ecoulement de puissance optimal [12] [02].

II- 6 Classification des méthodes d'optimisations :

La complexification croissante des problèmes d'optimisation, a entraîné le développement d'une grande quantité de méthodes de résolution. La globalité de ces techniques d'optimisation dans les différentes publications, se divise typiquement en deux grandes classes dont le premier classement les méthodes déterministes. Et une grande partie de l'effort de recherche, plus spécifiquement dans les domaines de la recherche opérationnelle et de l'Intelligence Artificielle, est consacré depuis une vingtaine d'années à la deuxième classe de méthodes d'optimisation : les métaheuristiques. La classification et illustrée dans la figure II -5 [13].

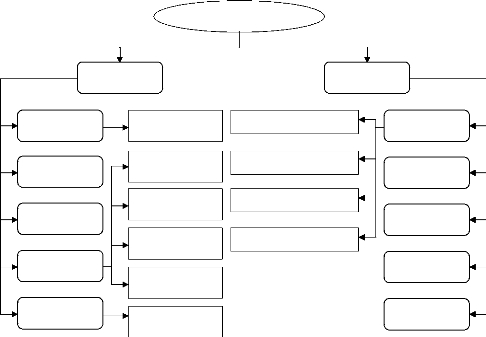
Les méthodes
déterministes

Les méthodes
stochastiques

Les méthodes d'optimisations

Les méthodes
heuristiques

Méthodes
Branch bounde

Méthodes
mathématiques

Simplex hook et
rosembrok

Direction
conjuguée

Plus grande
pente

Gradient
conjugué

^QuasiNewton

Réseau de
neurones

Les méthodes
évolutionnistes

Mante
carlo

Recuit
simulé

Recherche
taboue

Particule
d'essaim

Plan
d'expérience

Méthodes
D'apprentissage

Algorithme génétique

Stratégie d'évolution

Prog évolutionniste

Evolution différentielle

Figure II-6 : Classification des méthodes d'optimisations

II- 6. 1 Méthodes déterministes « locales » :

II-6. 1. 1 Les méthodes de gradient :

Historiquement, les méthodes de gradient sont les plus anciennes. Elles permettent de résoudre des problèmes non linéaires et sont basées sur une hypothèse fort : la connaissance de la dérivée de la fonction objectif en chacun des points de l'espace. Cette famille de méthodes procède de la façon suivante :

On choisit un point de départ x₀ et on calcule le gradient ?f (x₀ ) en x₀ . Comme le gradient indique la direction de plus grande augmentation de f , on se déplace d'une quantité ₀ dans le sens opposé au gradient et on définit le point x₁ :

x 1

? f x

( )

0

= -

x (II-16)

0 ⁰ f x

? ( )

0

Cette procédure est répétée et engendre les points x ₀ , x ₁ ,..., x_k . Ainsi, pas à pas, la distance entre le point d'indice k et l'optimum diminue.

? f x

( )

k

x + = -

x ou k

? , > 0

k (II-17)

1 k k k

? f x

( )

k

k est le pas de déplacement à chaque itération. Si _k est fixé, on parle de méthode de gradient à

pas prédéterminer. L'inconvénient de cette procédure est que la convergence est très dépendante du choix du pas de déplacement. La convergence peut être très lente si le pas est mal choisi. L'intérêt principal de cette méthode est de pouvoir se généraliser aux cas de fonctions non partout différentiables.

Actuellement, la méthode la plus usitée de cette famille est la méthode de la plus forte pente. Elle permet de se libérer du choix d'un _k mais elle introduit un critère d'arrêt. Le but de cette

méthode est de minimiser la fonction de :

g ( ) (

= f x k - . ? f x k

( ) ) (II-18)

- Algorithme de la plus forte pente :

a) Choisie un point de départ x₀ et faire k=0.

b) A l'itération k : d k = -?f( x _k). Recherche _k tel que :

f x

( . ) { ( . ) }

+ d Min f x

= + d pour = 0 x k + 1 = x _k + _k . d _k .

k k k k k k

c) Si le test d'arrêt est vérifié alors fin sinon k ? k + 1 et retourner en b).

L'algorithme de la plus forte pente est à la base de l'algorithme de Hill-climbing appelé également algorithme de descente de gradient [14].

II- 6. 1. 2 La méthode de Newton :

La méthode de Newton est une méthode très puissante à cause de sa convergence rapide au voisinage de la solution. Cette propriété est spécialement utile pour les applications dans les systèmes électriques. En effet, une estimation initiale proche de la solution est facile à obtenir.

Les niveaux de tensions peuvent êtres prises au voisinage des tensions nominales, les puissances généré estimées à partir des données historiques et les valeurs des prises de charges des transformateurs proches de 1.0 p.u.

- Développement du Lagrangien, du Gradient et du Hessien :

La solution du problème de l'optimisation par la méthode de Newton, nécessite l'utilisation des théorèmes de Lagrange et de Kuhn Tucker. Le lagrangien est formulé comme suit :

L z = f x +

( ) ( ) ( ) ( )

' g x + ' h x (II-19)

Avec : [ ]t

z = x , ,

X et jt sont respectivement les multiplicateurs de Lagrange et de Kuhn Tucker et h(x) inclut seulement les contraintes ( jti ? 0 et hi(x)=0 ).Le Gradient et le Hessien, du Lagrangien ( ?L et ? ) peuvent êtres définit comme suit

² L

( ) ( ) ? ? L z ? ? = z ?? ?? ? zi

(II-20)

?

? ?

i j

x

2

L ( )

Z

i j

? ?

i j

x

? 2 ( ) ( ) ( )

2 2

L Z ? L Z ? L Z

? ?

x x ? ?

x ? ?

x

i j i j

? 2 L Z

( ) 0 0

? ? ? ?

? ? ??

( ) ( )

? ? 2 L z ? 2 L z = ?

? ? ? ?

z z

i j

= =

H ?

?
?

?? ?

?

?

?

?

0 0 ? (II-21)

?
?

?? ?

Le Gradient est un vecteur constitué des premières dérivées partielles du Lagrangien. Et Le Hessien est une matrice carrée constituée des dérivées partielles secondes du Lagrangien. Le théorème de Kuhn Tucker donne les conditions nécessaires de la solution optimale z* [02].

- Algorithme :

L'organigramme suivant illustre la structure de l'algorithme newton. Nous détaillerons les diverses phases qui le constituent et présenterons tout les étapes.

Début

Lecture de donnée et estimation initiale

Mettre le nombre d'itération T=0

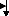
Calculer le Gradient et le
Hessien du Lagrangien.

T=T+1

Résoudre l'équation :

[ H ].ÄZ = ?L( Z)

ÄZ

Mettre à jour la solution:

Z nouveau = Z ancien -

Non

Si ÄZ =

Oui

Fin

Figure II-7 : Organigramme simplifié de l'algorithme de Newton

II- 6. 2 Les méthodes métaheuristiques (globale) :

II- 6. 2. 1 Mante Carlo :

C'est la plus simple des méthodes stochastiques. Elle consiste à tirer une solution au hasard à chaque itération. La fonction objective est évaluée en ce point. Si elle meilleure que l'optimum courant, cette valeur est enregistrée, ainsi que la solution correspondante et le processus continue jusqu'à ce que les condition d'arrêt soient vérifiées. Il s'agit donc d'un processus d'exploration.

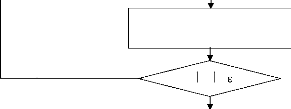
- Algorithme :

Début

Créé des solutions initiales

Evalue les solutions

Registrée la meilleur solution

Non Oui

Fin

Arrêt

Figure II-8 : Organigramme de la méthode Monte Carlo

Les méthodes Monte Carlo peuvent être utilisées, en première approche, pour avoir des renseignements utiles sur la forme de la fonction. Elle permet par exemple de choisir de façon plus appropriée le point de départ d'un algorithme de recherche locale. Toutefois, cette association ne garantit pas la localisation de l'optimum global [15].

II- 6. 2. 2 Recuit Simulé :

Le recuit simulé est une version améliorée de la méthode d'amélioration itérative. Il a été proposé en 1983 par Kirkpatrick pour la résolution des problèmes d'optimisation. La méthode imite le principe thermodynamique. Elle s'inspire du phénomène physique de refroidissement lent d'un corps en fusion qui le conduit à un état solide de basse énergie.

Un métal est chauffé à une température très élevée, il devient liquide et peut occuper toute configuration. Quand la température décroît, le métal va se figer peu à peu dans une configuration qu'il de plus en plus difficile à déformer, il est refroidi. En le réchauffant (recuit), le métal peut être retravaillé de nouveau pour lui donner la forme désirée. Il faut baisser lentement la température en marquant des palies suffisamment longs pour que le corps atteigne l'équilibre thermodynamique à chaque palier de la température, ce qui permet d'obtenir à la fin processus un matériau dans un état cristallin bien ordonné correspondant à un état d'énergie minimum. Par contre, si la baisse de température se fait de manière trop brutale, le matériau est amorphe et ses atomes sont figés dans un état désordonné traduisant un minimum local d'énergie [15].

II- 6. 2. 2. 1 Température initiale

La température initiale est choisie arbitrairement par le programmeur, il est souvent nécessaire de tester l'algorithme pour choisir la bonne température initiale.

II- 6. 2. 2. 3 Modification élémentaire

La modification élémentaire permet de faire évoluer la solution. Une fois cette modification effectuée, il nous faut calculer la nouvelle valeur de l'énergie du système et faire la différence avec l'ancienne.

II- 6. 2. 2. 4 Paramètres :

La principale difficulté rencontrée dans la résolution d'un problème d'optimisation par cette méthode est liée à la détermination du schéma de refroidissement. L'ensemble des paramètres qui gouvernent la convergence de l'algorithme sont :

· Valeur initiale du paramètre de contrôle T0 (température initiale)

· Facteur de réduction de la température rt

· Nombre d'itérations à température constante (longueur de la chaîne de Markov) Lm

· Taille de voisinage N_s

· Critère d'arrêt

Début

II- 6. 2. 2. 5 Algorithme :

L'organigramme suivant expose l'algorithme du recuit simulé. Les sections suivantes détaillent et expliquent l'organigramme.

Configuration initiale

Température initiale T

Fin

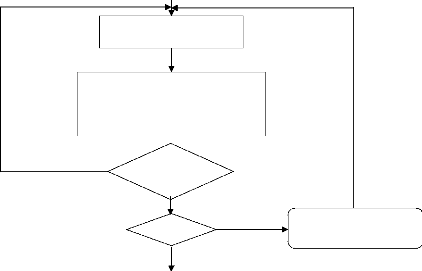
Non

Règle d'acceptation de Metropolis :
- Si ÄE = 0 : modification accepté

- Si ÄE > 0 : modification accepté

Modification élémentaire
Variation d'énergie ÄE

Oui

Equilibre
thermodynamique

Oui

Système figé

Non

Programme du recuit
Diminution lente
de T

Figure II -9 : Organigramme de l'algorithme du recuit simulé.

II-6. 2.3 La méthode tabou :

La recherche tabou est une métaheuristique d'optimisation présentée par Fred Glover en 1986. On trouve souvent l'appellation recherche avec tabous en français.

- Principe :

L'idée de la recherche tabou consiste, à partir d'une position donnée, à en explorer le voisinage et à choisir la position dans ce voisinage qui minimise la fonction objectif. Il est essentiel de noter que cette opération peut conduire à augmenter la valeur de la fonction, c'est le cas lorsque tous les points du voisinage ont une valeur plus élevée.

C'est à partir de ce mécanisme que l'on échappe aux minima locaux. Le risque cependant est qu'à l'étape suivante, on retombe dans le minimum local auquel on vient d'échapper. C'est pourquoi il faut que l'heuristique ait de la mémoire, le mécanisme consiste à interdire (d'où le nom de tabou) certains mouvements ou certaines composantes de ce mouvement (l'exemple le plus simple est d'interdire les derniers mouvements).

Les positions déjà explorées sont conservées dans ce qu'on appel la Liste Tabou d'une taille donnée, qui est un paramètre ajustable de l'heuristique [17].

- Les tabous :

Les tabous sont une manière de représenter la mémoire du cheminement effectué pour diriger l'exploration vers des régions non visitées.

La manière la plus simple de définir les tabous est de conserver une liste T des card. (T) dernières solutions rencontrées et on empêche la procédure d'y retourner. On gère cette liste comme une liste circulaire : on élimine le plus vieux tabou et on insère la nouvelle solution (cette solution peut s'avérer coûteuse en termes de quantité d'information requise).

On peut alors définir les tabous en fonction des "transformations" permettant de passer d'une solution à une autre. Ainsi, on garde une liste des card. (T). dernières transformations effectuées et on s'interdit de les inverser.

- Algorithme :

La méthode consiste à se déplacer d'une solution vers une autre par observation du voisinage de la solution de départ et à définir des transformations tabous que l'on garde en mémoire. Une transformation tabou est une transformation que l'on s'interdit d'appliquer à la solution courante.

Début

Nouvelle configuration courante s = t

Insertion du mouvement
t ? s dans la liste tabou

Configuration initiale s

Liste Tabou initiale vide

Perturbation de s suivant N mouvements non tabous : Evaluation des N voisins

Sélection du meilleur voisin t

Actualisation de la meilleure solution connue

Non

Critère d'arrêt atteint

_Oui

Fin

Figure II-10 : Organigramme de l'algorithme de tabou simple.

II- 6. 2. 4 Les méthodes évolutionnistes :

Les Algorithmes Evolutionnaires.Comprend principalement, en plus des Algorithmes Génétiques, les Stratégies d'évolution (en anglais Evolution Stratégies, souvent désignées par ES), la programmation Evolutionnaire (en anglais Evolutionnary Programming, EP) et la Programmation Génétique (en anglais Genetic Programming, GP) [17].

Algorithmes Evolutionnair

Algorithmes Génétiques		Stratégies d'Evolution		Programmation Génétique		Programmation Evolutionnaire

Figure II-11 : Principales catégories des Algorithmes Evolutionnaires

II- 6. 2. 4. 1 Stratégies d'Evolution (ES) :

Les premiers efforts pour la mise en place des Stratégies d'Evolution (SE) ont eu lieu dans les années 60 en Allemagne par Rechenberg en 1973 et Schwefel 1981. Ces algorithmes s'appuient sur une représentation en nombres réels et de dimension fixe des individus, ainsi que sur un opérateur de mutation gaussienne. Les ES les plus performantes utilisent les mutations auto adaptatives, dans lesquelles chaque individu porte avec lui les paramètres de la mutation gaussienne qui lui sera appliquée - paramètres eux-mêmes soumis à mutation.

II- 6. 2. 4. 2 Programmation Génétique (GP) :

Proposée par Cramer en 1985, la Programmation Génétique (GP) a surtout été popularisée par Koza au début des années 90. Elle s'intéresse à l'évolution de programmes. Elle propose un paradigme permettant la programmation automatique d'ordinateurs par des heuristiques basées sur les mêmes principes d'évolution que les AG. La différence entre la GP et les AG réside essentiellement dans la représentation des individus. En effet, la GP consiste à faire évoluer des individus dont la structure est similaire à celle des programmes informatiques.

Koza représente les individus sous forme d'arbres, c'est-à-dire de graphes orientés et sans cycle, dans lesquels chaque noeud est associé à une opération élémentaire relative au domaine du problème. La PG est particulièrement adaptée à l'évolution de structures complexes de dimensions variables.

II- 6. 2. 4. 3 Programmation Evolutionnaire (EP) :

La Programmation Evolutionnaire (PE) est introduite dans les années 60 par L. Fogel, puis étendue par Burgin, Atmar et d'autres. Elle a été conçue dans le but de faire évoluer des machines à états finis, puis a été étendue aux problèmes d'optimisation de paramètres. Cette approche met l'emphase sur la relation entre les parents et leurs descendants plutôt que sur les opérateurs génétiques. Elle a été utilisée dans de nombreux autres champs d'application. Les caractéristiques de l'évolution sont très proches de celles des SE. Contrairement aux trois autres AE classiques, la PE n'utilise pas une représentation spécifique des individus mais plutôt un modèle évolutionnaire de haut niveau, qui est associé à une représentation et à un opérateur de mutation directement appropriés au problème à résoudre.

I-7 Conclusion

Dans ce chapitre, on a exposé la formulation mathématique générale du problème de la répartition optimale de puissance, qui se traduit par un problème d'optimisation d'une fonction objective sujet à des contraintes. La plupart des équations formulant ce problème sont non linéaire, de ce fait, il est nécessaire d'utiliser une technique de programmation non linéaire pour la résolution du problème.

CHAPlTRE lll

Les méthodes

métaheuristiques

III --Les méthodes métaheuristiques

III - 1 Introduction

Ce chapitre est consacré à la présentation les algorithmiques génétiques et la méthode de particules d'essaim pour la résolution du problème d'optimisation de l'écoulement de puissance dans le système électrique. Les algorithmes génétiques sont des algorithmes d'optimisation s'appuyant sur des techniques dérivées de la génétique et de l'évolution naturelle1 : croisements, mutations, sélection, etc. Les algorithmes génétiques ont déjà une histoire relativement ancienne, puisque les premiers travaux de John Holland sur les systèmes adaptatifs remontent à 1962.

III -2 Les algorithmes génétiques

Un algorithme génétique recherche le ou les extrema d'une fonction défini sur un espace de données. Pour l'utiliser, on doit disposer des cinq éléments suivants :

1. Un principe de codage de l'élément de population. Cette étape associe à chacun des points de l'espace d'état une structure de données. Elle se place généralement après une phase de modélisation mathématique du problème traité. Le choix du codage des données conditionne le succès des algorithmes génétiques. Les codages binaires ont été très employés à l'origine. Les codages réels sont désormais largement utilisés, notamment dans les domaines applicatifs, pour l'optimisation de problèmes à variables continues.

2. Un mécanisme de génération de la population initiale. Ce mécanisme doit être capable de produire une population d'individus non homogène qui servira de base pour les générations futures. Le choix de la population initiale est important car il peut rendre plus ou moins rapide la convergence vers l'optimum global. Dans le cas oft l'on ne connaît rien du problème à résoudre, il est essentiel que la population initiale soit répartie sur tout le domaine de recherche.

3. Une fonction à optimiser. Celle-ci prend ses valeurs dans R+ et est appelée fitness ou fonction d'évaluation de l'individu. Celle-ci est utilisée pour sélectionner et reproduire les meilleurs individus de la population.

4. Des opérateurs permettant de diversifier la population au cours des générations et d'explorer l'espace d'état. L'opérateur de croisement recompose les gènes d'individus existant dans la population, l'opérateur de mutation a pour but de garantir l'exploration de l'espace d'état.

5. Des paramètres de dimensionnement : taille de la population, nombre total de générations ou critère d'arrêt, probabilités d'application des opérateurs de croisement et de mutation [18].

Principe

Un algorithme génétique est un algorithme itératif de recherche d'optimum, il manipule une population de taille constante. Cette population est formée de points candidats appelés chromosomes. La taille constante de la population entraîne un phénomène de compétition entre les chromosomes. Chaque chromosome représente le codage d'une solution potentielle au problème à résoudre, il est constitué d'un ensemble d'éléments appelés gènes, pouvant prendre plusieurs valeurs appartenant à un alphabet non forcément numérique [19] [20].

A chaque itération, appelée génération, est créée une nouvelle population avec le même nombre de chromosomes. Cette génération consiste en des chromosomes mieux "adaptés" à leur environnement tel qu'il est représenté par la fonction sélective. Au fur et à mesure des générations, les chromosomes vont tendre vers l'optimum de la fonction sélective. La création d'une nouvelle population à partir de la précédente se fait par application des opérateurs génétiques que sont : la sélection, le croisement et la mutation. Ces opérateurs sont stochastiques [20].

III - 2.1 Codage des chromosomes et décodage

Il y a plusieurs types de codage : binaire, réel, codage de gray et codage dynamique des paramètres. Chacun ayant ses propres avantages et inconvénients. Les plus utilisés sont présentés ci-dessous.

III -2.1.1 Codage binaire

Holland et de Jong ont imposé le codage binaire de longueur fixe pour un chromosome qui s'écrit sous la forme d'une chaîne de l bits avec

n

l=?₌ ( )

l x_i

i 1

Où l ( x_i ) est le nombre de bits du gène numéro i correspondant au paramètre x_i .

Un des avantage du codage binaire est que l'on peut ainsi facilement coder toutes sortes de paramètre : réel, entiers booléens et chaînes de caractère. Cela nécessite simplement l'usage de fonction de codage et décodage pour passer d'une présentation à l'autre. Ce choix le rend virtuellement applicable à tous les problèmes dont les solutions sont numériques, c'est-à-dire calculées par ordinateur.

Le génotype d'un individu caractérise la structure du chromosome tandis que le phénotype désigne la chaîne obtenue par la concaténation des paramètres réels ou gênes(x₁ , x ₂, x₃, ...) .

Le décodage convertit le chromosome en phénotype grâce au génotype. Les valeurs des paramètre sont extraites sont extraites du phénotype et ensuite fournies à la fonction d'adaptation qui retourne la performance permettant ainsi de classer l'individu dans la population.

Le phénotype est obtenu à partir du génotype par l'équation :

im

? l- xim

2j + x

x_i = 2 l( xi) -1 ?j=0

( x)

b est le j^eme bit dans le gène numéro i.

Cette méthode de codage est relativement facile à implanter mais elle présente l'inconvénient de limiter la précision des paramètres à une valeur correspondant à l'écart entre deux configurations réelles adjacentes obtenues, pour une variation du bit le moins significatif. On constate que la précision du codage dépend du nombre de bits utilisé. Pour un nombre de bits par gène valant 8, 16 et 32, les précisions relatives valent ,1.5.10^-5 et 2.3.10^-10, respectivement.

A chaque paramètre x_i , on associe un gène g_i qui est un entier obtenue par :

g i

- x im x iM -x im

. ( 2 ( ) - 1) l xi

III -2.1.2 Codage de gray

Avec le codage binaire, deux configurations proches dans l'espace des paramètres peuvent avoir deux chromosomes très distincts, par exemple, les chaînes « 01111 » et « 10000 » correspondent à deux configurations réelles voisines alors qu'elles diffèrent de cinq bits. Cette caractéristique peut s'avérer pénalisante pour la recherche locale par croisement.

L'utilisation de code gray a été recommandée pour répondre à ce problème. En effet, avec ce code, les entiers adjacents ne différents que d'un bit. Le passage entre deux configurations réelles voisines ne nécessite que de modifier un seul bit dans le chromosome.

Le passage du code binaire au code de gray est effectué de la manière suivante :

? b sij l x sij l x

= ( ) ( )

=

gray j

b i i

= ??

j ? - =

1 ( )

? b b sij l x

j j i

Où ? représente l'addition modulo 2.

La transformation inverse s'obtient avec l'équation suivante :

b

) gray

b_k

= ? =

l x

( i

j k j

Si on considère que le chromosome est représenté en code de gray, on effectuera d'abord la transformation avant un décodage binaire standard.

Ces opérations sont transcrites dans la table III-1.

Entier	Code binaire	Code Gray
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

Tab III- 1 : Code binaire et code gray sur 4 bits

L'intérêt du codage de Gray se comprend mieux lorsque les opérateurs de croisement et de mutation sont présentés.

III -2.1.3 Codage dynamique des paramètres

Pour résoudre le problème de précision inhérent au décodage binaire standard et améliorer la recherche locale, un codage dynamique des paramètres est proposé. La procédure de décodage est la suivante :

x_i

? l x i

x x ( )

- ?

iM im j

= +

x ? + ( ) ?

2 ( )

i ?= 2 . b dN x

im l x j i

- 1 ? j 0 ?

Où dN(x_i ) est une variable réelle aléatoire à densité de probabilité uniforme prise, dans l'intervalle [ 0,1]

L'introduction de dN(x_i ) supprime donc les discontinuités entre deux configuration réelles

adjacentes, obtenues pour une variation du bit le moins significatif, en proposant une valeur aléatoire [21] [15].

III -2.1.4 Codage réel

Dans le cas du codage binaire, des difficultés surviennent pour calculer la fonction objectif et traiter les problèmes à variables :

a. Les fonctions objectifs sont exprimées sous forme réelle. Les chromosomes binaires doivent alors être convertis à chaque évaluation.

b. Les problèmes multi-variables sont ramenés à des problèmes mono variable par concaténation des inconnues en un seul chromosome. A chaque évaluation, la chaîne de bits résultante doit alors être découpée en autant de sous-chaînes qu'il y a d'inconnues. Ces sous-chaînes sont converties en nombres réels pour l'évaluation de la fonction objectif.

Une solution est tout simplement de représenter l'ensemble des variables par un vecteur x = ( x₁ , x ₂ , x₃ ,...x_n ) où chaque x_i est une nombre réel. Cette façon de faire est le codage réel. Il

emploie à cet effet des mécanismes plus adaptés, reposant principalement sur une représentation réelle des chromosomes [15].

III - 2.2 Fonction d'évaluation

La phase d'évaluation consiste à calculer la << force >> d'adaptation de chaque individu de la population (i.e. son adaptation aux contraintes de l'environnement dans un processus évolutif naturel). Un algorithme génétique tend donc à maximiser la force des individus au cours des populations successives pour aboutir à une population très bien adaptée à son environnement, c'est-à-dire à un ensemble de très bonnes solutions pour le problème posé.

Si Le problème consiste à trouver le minimum de la fonction objectif. Chaque Xi est limitée par une limite inférieure Xi min et une limite supérieure Xi max. la fonction objective est bornée supérieurement, on va choisir une fonction sélective à maximiser de la forme suivante [22] [23] :

fitness

on

0 sin

? -

F max ( ).... . . . ( ) max

F x si F x F

<

= ?

?

( III - 1 6)

III - 2.3 Sélection

Cet opérateur est chargé de définir quels seront les individus qui vont être dupliqués dans la nouvelle population et vont servir de parents (application de l'opérateur de croisement). Soit n le nombre d'individus, on doit en sélectionner n/2 (l'opérateur de croisement nous permet de repasser à n individus). Cet opérateur est peut-être le plus important puisqu'il permet aux individus d'une population de survivre, de se reproduire ou de mourir. En règle général la probabilité de survie d'un individu sera directement reliée à son efficacité relative au sein de la population.

On trouve essentiellement quatre types de méthodes de sélection différentes : La méthode de la "loterie biaisée", la méthode "élitiste" la sélection par tournois et la sélection universelle stochastique.

III - 2.3.1 La loterie biaisée ou roulette Wheel

Cette méthode est la plus connue et la plus utilisée. Avec cette méthode chaque individu a une chance d'être sélectionné proportionnelle à sa performance, donc plus les individus sont adaptés au problème, plus ils ont de chances d'être sélectionnés. Pour utiliser l'image de la "roue du forain", chaque individu se voit attribué un secteur dont l'angle est proportionnel à son adaptation, sa "fitness". On fait tourner la roue et quand elle cesse de tourner on sélectionne l'individu correspondant au secteur désigné par une sorte de "curseur", curseur qui pointe sur un secteur particulier de celle-ci après qu'elle se soit arrêté de tourner [24].

Figure III-1 : Sélection par la méthode de la roue de loterie.

III - 2.3.2 La méthode élitiste

Cette méthode consiste à sélectionner les n individus dont on a besoin pour la nouvelle génération P' en prenant les n meilleurs individus de la population P après l'avoir triée de manière décroissante selon la fitness de ses individus. Il est inutile de préciser que cette méthode est encore pire que celle de la loterie biaisée dans le sens où elle amènera à une convergence prématurée encore plus rapidement et surtout de manière encore plus sûre que la méthode de sélection de la loterie biaisée ; en effet, la pression de la sélection est trop forte, la variance nulle et la diversité inexistante, du moins le peu de diversité qu'il pourrait y avoir ne résultera pas de la sélection mais plutôt du croisement et des mutations.

III - 2.3.3 La sélection par tournois

Cette méthode est celle avec laquelle on obtient les résultats les plus satisfaisants. Le principe de cette méthode est le suivant : on effectue un tirage avec remise de deux individus de P, et on les fait "combattre". Celui qui a la fitness la plus élevée l'emporte avec une probabilité p compris entre 0.5 et 1. On répète ce processus n fois de manière a obtenir les n individus de P' qui serviront de parents. La variance de cette méthode est élevée et le fait d'augmenter ou de diminuer la valeur de p permet respectivement de diminuer ou d'augmenter la pression de la sélection.

III - 2.3.4 La sélection universelle stochastique

Cette méthode semble être très peu utilisée et qui plus est possède une variance faible, donc introduit peu de diversité, nous n'entrerons donc pas dans les détails, on se contentera d'exposer sa mise en oeuvre. On prend l'image d'un segment découpé en autant de sous segments qu'il y a d'individus. Les individus sélectionnés sont désignés par un ensemble de points équidistants [24].

III - 2.4 Le croissement

Dans un algorithme génétique, des parties des individus sélectionnés (parents) sont échangées par croisement. Le croisement peut être effectué sur un ou plusieurs parents pour former un ou plusieurs enfants (ou descendants). Il existe, là aussi, de nombreuses méthodes de croisement.

Nous présentons ici les croisements classiques, qui sont le croisement en un point, le croisement en deux points et le croisement uniforme, il y à d'autres méthodes de croisement appelées le croisement diagonal et le croisement de bloc. Ces derniers opérateurs sont bien adaptés à la transmission des propriétés topologiques entre les parents et les descendants [25].

III - 2.4.1 Croisement en un point

On choisit au hasard un point de croisement, pour chaque couple figure III-2. Notons que le croisement s'effectue directement au niveau binaire, et non pas au niveau des gènes. Un chromosome peut donc être coupé au milieu d'un gène.

2 parents 2 enfants

10010

1001101011

10000

011010111

100100

001101

100100 10101001001

001101 10011010111

Figure III-2 : Principe de croissement en un point

III - 2.4.2 Croisement en un et deux points

On choisit au hasard deux points de croisement figure III-3. Par la suit, nous avons utilisé cet opérateur car il est généralement considéré comme plus efficace que la précédent. Néanmoins nous n'avons pas constaté de différence notable dans la convergence de l'algorithme.

Notons que d'autre formes de croisement existent, du croisement en K points jusqu'au cas limite du croisement uniforme.

2 parents 2 enfants

10101

001101

100100

001001

010111

10011

100100 10101 001001

001101 10011 010111

Figure III-3 : Principe de croissement en deux points

III - 2.4.3 Croisement uniforme

Le croisement binaire utilise un masque (en binaire) de même longueur que les parents. Chaque 1 contenu dans le masque déclenche de l'inversion du gène visé avec celui de l'autre parent. Voir le figure III-4 [25] :

0 0 0 1 1 1

Masque

2 enfants

0

0 0 1 0 0 1

0 010 0

0 1 0 1 1 1

011 0 1

1

1 0 0		0 0	0 1		1 1		0 0
2 parents
1 0 0		1 0	0 1		0 1		0 1
0 0 1		1 0	1 1		0 0		1 1
100	01 00			1		110 1
100	1 10 1			0		1 1 00

Figure III-4 : Croisement uniforme

III - 2.5 Mutation

Nous définissons une mutation comme étant l'inversion d'un bit dans un chromosome. Cela revient à modifier aléatoirement la valeur d'un paramètre du dispositif. Les mutations jouent le rôle de bruit et empêchent l'évolution de se figer. Elles permettent d'assurer une recherche aussi bien globale que locale, selon le poids et le nombre des bits mutés. De plus, elles garantissent mathématiquement que l'optimum global peut être atteint.

1 0 0 1 0 0

1 0 0 1 0 0

0 1 0 1 0 0 1 0 0 1

0 0 1 0 1 0 0 1 0 0 1

Une mutation

1 1

Figure III-5 : Opérateur de mutation

Début

III - 2.6 Organigramme de la procédure génétique

L'organigramme fonctionnel de la figure III-6 illustre la structure de l'algorithme génétique standard. Nous détaillerons les diverses phases qui le constituent et présenterons les mécanismes associés à chacune d'entre elles dans les sections suivantes [26].

Population initiale

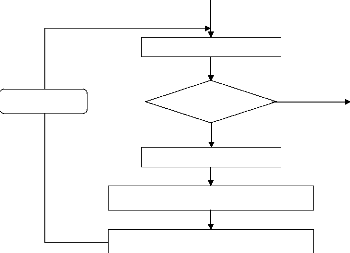
T=T+1

Recombinaison : Croisement

Nouvelle Population

Non

Evaluation

Terminer

Sélection

Oui

Résultat

Figure III-6 : Organigramme d'un algorithme génétique.

III - 2.7 Application de l'AG à la répartition économique des puissances

Nous appliquons ici l'algorithme génétique de base étape par étape à la répartition économique des puissances sur un simple réseau test constitué de 9 jeux de barres, 6 lignes électriques, 3 générateurs, 3 transformateurs et 3 charges.

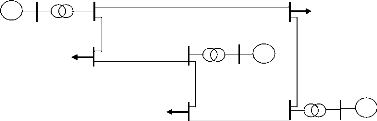
G

G

G

Figure III-7 : Schéma unifilaire de réseau électrique

Le tableau III-2 montre les données techniques et économiques des trois générateurs interconnectés. La puissance de base utilisée est de 100 MVA.

° N	Pmin ( Pu )	Pmax ( Pu )	($ / h )	( $ / Mwhr)	( Mw^2 hr) $ /
1	0.30	1.8	105.0	2.45	0.01
2	0.15	0.9	44.1	3.51	0.01
3	0.40	1.9	40.6	3.89	0.01

Tableau III-2 : Ensemble des paramètres des puissances actives générées PGi

Le problème de la REP consiste à trouver le minimum de la fonction objective. Chaque puissance active générée PGi est limitée par une limite inférieure PGi min et une limite supérieure PGi max . Puisque la

fonction objective est bornée supérieurement, on va choisir une fonction sélective à maximiser de la forme suivante [22] :

fitness

? F - F x ( ) si F x ( ) < max = ? ?0 sinon

Fmax

III - 2.7.1 Codage des chromosomes et le décodage

La première étape consiste à coder les variables P_Gi sous forme de chromosome. Pour sa simplicité et sa commodité, le codage binaire est utilisé dans cet exemple. Avec le codage binaire, les puissances actives générées du réseau test(PG ₁ , P _G2 , P_G3) vont être codées comme une chaîne de « 0 » et « 1 » avec,

respectivement, des longueurs(L₁ , L ₂ , L ₃ ) (peuvent être différentes).

Chaque paramètre P_Gi a une limite supérieure PGi max = B et une limite inférieure PGi min = A. Le choix de L1,L ₂ et L₃ pour les paramètres est sujet de la résolution spécifiée par l'utilisateur dans l'espace de la

recherche. Avec le codage binaire, la relation entre la longueur de bit Li et la résolution correspondante Ri est donnée par :

R i	=	B A - i I
		2 - 1 Li

Donc, l'ensemble P_Gi peut être transformé en une chaîne binaire (chromosome) avec une longueur

? L_i et puis l'espace de recherche est exploré. Il est à noter que chaque chromosome présente une solution possible du problème. Par exemple, supposer le domaine des paramètres de (PG ₁ , P _G2 , P_G3) qui est présenté dans le Tableau 1. Si la résolution R ₁ , R ₂, R₃ est spécifiée comme 0.1, 0.05, 0.1 d'après l'équation (7) on aura L₁, L ₂ et L₃ = (4,4,4) . Alors l'ensemble de paramètres (PG ₁ , P _G2 , P_G3 ) peut être codé selon le tableau III-3.

N°	P1 (Pu)	Code	P2 (Pu)	Code	P3 (Pu)	Code
1	0.3	0000	0.15	0000	0.4	0000
2	0.4	0001	0.20	0001	0.5	0001
3	0.5	0010	0.25	0010	0.6	0010
4	0.6	0011	0.30	0011	0.7	0011
5	0.7	0100	0.35	0100	0.8	0100
6	0.8	0101	0.40	0101	0.9	0101
7	0.9	0110	0.45	0110	1.0	0110
8	1.0	0111	0.50	0111	1.1	0111
9	1.1	1000	0.55	1000	1.2	1000
10	1.2	1001	0.60	1001	1.3	1001
11	1.3	1010	0.65	1010	1.4	1010
12	1.4	1011	0.70	1011	1.5	1011
13	1.5	1100	0.75	1100	1.6	1100
14	1.6	1101	0.80	1101	1.7	1101
15	1.7	1110	0.85	1110	1.8	1110
16	1.8	1111	0.90	1111	1.9	1111

Tableau III-3 : Codage de l'ensemble des paramètres de PGi

Pour construire un codage multi-paramétrié, on peut tout simplement concaténer autant de codage d'un seul paramètre qu'il est nécessaire. Le chromosome correspond à l'ensemble de paramètres (1.7, 0.30, 1.1) est alors la chaîne de caractères binaire suivante 111000110111. Le décodage est la procédure inverse

III- 2.7.2 Tirage et évaluation de la population initiale

La première étape de tout algorithme génétique est de produire la population initiale. Une chaîne de caractères binaire de longueur l est associée à chaque membre (individu) de la population. D'habitude, la chaîne de caractères est connue comme un chromosome et représente une solution du problème. Un échantillonnage de cette population initiale crée une population intermédiaire. Nous fixons la taille de la population à N = 4. Nous tirons donc de façon aléatoire 4 chromosomes sachant qu'un chromosome est composé de 12 bits, et chaque bit dispose d'une probabilité '/2 d'avoir une valeur 0 ou 1. Le minimum, 1226.5 ($/hr), est atteint par la deuxième séquence et le maximum, 1756.1 ($/hr), est atteint par la troisième séquence TableauIII-4.

Voyons comment l'algorithme va tenter d'améliorer ce résultat.

N°	Population initiale	P1 ( pu)	P2 (pu)	P3 (pu)	F (x )( $ / h)	F max - F(x)
1	000111111100	0.4	0.90	1.60	1579.0	177.10
2	000100101011	0.4	0.30	1.50	1226.5	529.60
3	101010011011	1.3	0.65	1.50	1756.1	0.000
4	111001010111	1.7	0.45	1.10	1622.3	133.80

Tableau III-4 : Processus de la première génération de l'AG pour le réseau 9 noeuds

Donc quelques opérateurs (reproduction, croisement et mutation) sont appliqués à cette population pour obtenir une nouvelle population. Le processus qui commence de l'actuelle population et aboutit à la nouvelle population, est nommé une génération [22].

III-2.7.3 Sélection

La sélection est appliquée afin de favoriser au cours du temps les individus les mieux adaptés, à les mieux adapté, Une nouvelle population va être créée à partir de l'ancienne par le processus de sélection de la roue de loterie biaisée. Nous tournons cette roue 4 fois et nous obtenons à la fin la nouvelle population décrite dans le tableau III-5 [23] [22].

N°	Les séquences de la population initiale	Les séquences de la Nouvelle population
1	000111111100	000100101011
2	000100101011	000111111100
3	101010011011	111001010111
4	111001010111	000100101011

Tableau III-5 : Nouvelle Population

III-2.7.4 Croisement

Le croisement est un opérateur très important des algorithmes génétiques. Nous tirons aléatoirement un lieu de croisement dans la séquence. Le croisement s'opère alors à ce lieu avec une probabilité Pc par exemple égale 1. Le tableau III-6 donne les conséquences de cet opérateur [23] [22]

	Locus l=3		Locus l=7
Parent 1	000100101011	Parent 2	000111111100
Parent 3	111001010111	Parent 4	000100101011
Enfant 1	000001010111	Enfant 1	000111101011
Enfant 2	111100101011	Enfant 2	000100111100

Tableau III-6 : Résultats de croisement pour deux locus différents

III-2.7.5 Mutation

Dans cet exemple à codage binaire, Le rôle de la mutation est d'introduire de nouvelles caractéristiques génétiques, ou de les réintroduire, en modifiant quelques gènes des individus enfants. Nous tirons ainsi pour chaque bit un chiffre aléatoire entre 0 et 1 et si ce chiffre est inférieur à Pm alors la mutation s'opère. Le tableau III-7, avec Pm = 0.05, met en évidence ce processus [27] [22].

	1	2	3	4	5	6	7	8	9	10	11	12
000001010111	0.28	0.26	0.70	0.78	0.98	0.47	0.90	0.45	0.80	0.82	0.16	0.39	000001010111
111100101011	0.52	0.71	0.56	0.46	0.44	0.08	0.44	0.36	0.30	0.85	0.75	0.94	111100101011
000111101011	0.55	0.01	0.59	0.81	0.97	0.22	0.70	0.52	0.93	0.71	0.22	0.44	010111101011
000100111100	0.17	0.96	0.35	0.04	0.75	0.89	0.28	0.25	0.93	0.13	0.94	0.70	000000111100

Tableau III-7 : Mutation avec simple tirage aléatoire pour chaque bit entre 0 et 1

III-2.7.6 Retour à la phase d'évaluation

Le minimum est maintenant de 977.5 $/h (séquence 1).Nous sommes donc passé de 1226.5 $/h à 977.5 $/h

N°	Population initiale	P1 ( pu)	P2 (pu)	P3 (pu)	F (x )( $ / h)	F max - F(x)
1	000001010111	0.3	0.40	1.10	977.5	879.700
2	111100101011	1.8	0.25	1.50	1857.2	0.000
3	010111101011	0.8	0.85	1.50	1628.8	228.400
4	000000111100	0.3	0.30	1.60	1264.9	592.300

Tableau III-8 : Nouvelle évaluation

Après une seule génération tableau III-8. Bien sûr, nous devons recommencer la procédure à partir de l'étape de sélection jusqu'à ce que le minimum global soit obtenu, ou bien qu'un critère d'arrêt ait été satisfait. Il faut remarquer qu'on n'a pas pris en considération toutes les contraintes possibles. Finalement, il faut remarquer que si les AG convergent vers une solution optimale rien ne permet de dire, quand cette solution est inconnue, que le résultat soit la solution optimale. En outre, les AG peuvent rester longtemps proches de la solution optimale sans l'atteindre. C'est la raison pour laquelle de nombreuses méthodes dites hybrides, combinant les AG et les méthodes traditionnelles de gradient, sont de plus en plus utilisées. Enfin, la durée de calcul (temps CPU) peut être longue [22].

III- 3 Optimisation par essaim de particulaire

Les algorithmes « d'optimisation par essaim de particules » (Particle Swarm Optimization - PSO) introduits pour la première fois par Kennedy et Eberhart [Kennedy, 1995 ; Eberhart 2001] sont inspirés des déplacements collectifs observés chez certains animaux sociaux tels que les poissons et les oiseaux migrateurs. En effet, il est étonnant de voir comment ces animaux se déplacent en groupe dans une seule direction, se divisent parfois en plusieurs groupes afin d'éviter un obstacle ou un prédateur, puis reforment un groupe compact. Avec des règles locales très simples comme « rester proche des autres individus », « aller dans la même direction », « aller à la même vitesse », ces animaux sont capables d'éviter un prédateur par des mouvements d'explosion puis re-forment le groupe originel, tout en maintenant la cohésion du banc. Dans l'algorithme à essaim de particules, les individus de l'algorithme sont appelés particules et la population est appelée essaim [28].

III-3.1 Principe Caractéristiques

L'optimisation par essaim de particules repose sur un ensemble d'individus originellement disposés de façon aléatoire et homogène, que nous appèlerons dès lors des particules, qui se déplacent dans l'hyperespace de recherche et constituent, chacune, une solution potentielle. Chaque particule dispose d'une mémoire concernant sa meilleure solution visitée ainsi que la capacité de communiquer avec les particules constituant son entourage. A partir de ces informations, la particule va suivre une tendance faite, d'une part, de sa volonté à retourner vers sa solution optimale, et d'autre part, de son mimétisme par rapport aux solutions trouvées dans son voisinage.

A partir d'optimums locaux et empiriques, l'ensemble des particules va, normalement, converger vers la solution optimale globale du problème traité. Ce modèle présente quelques propriétés intéressantes, qui en font un bon outil pour de nombreux problèmes d'optimisation, particulièrement les problèmes fortement non linéaires, continus ou mixtes (certaines variables étant réelles et d'autres entières) :

1) Il est facile à programmer, quelques lignes de code suffisent dans n'importe quel langage évolué.

2) Il est robuste (de mauvais choix de paramètres dégradent les performances, mais n'empêchent pas d'obtenir une solution).

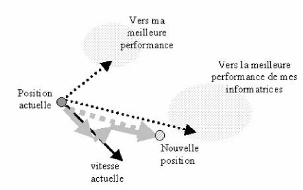
Figure III-9 : Schéma de principe du déplacement d'une particule.

Signalons, de plus, qu'il existe des versions adaptatives qui évitent même à l'utilisateur la peine de définir les paramètres (taille de l'essaim, taille des groupes d'informatrices, coefficients de confiance). L'une de ces méthodes (Tribes) est décrite en détail dans un des documents téléchargeables à partir du site du séminaire OEP'03. Son code source est disponible via le site Particle Swarm Central.

III -3.2 Topologie du voisinage

Le voisinage constitue la structure du réseau social. Les particules à l'intérieur d'un voisinage communiquent entre-elles. Différents voisinages ont été étudiés (Kennedy, 1999) et sont considérés en fonction des identificateurs des particules et non des informations topologiques comme les distances euclidiennes dans l'espace de recherche [15] :

A. Topologie en étoile : chaque particule est reliée à toutes les autres. l'optimum du voisinage est l'optimum global.

B. Topologie en anneau : chaque particule est reliée à n particules (en général, n =3), c'est la topologie la plus utilisée.

C. Topologie en rayon : les particules ne communiquent qu'avec une seule particule centrale

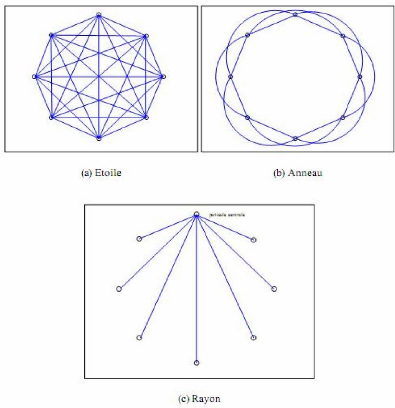
Figure III-10 : (a) anneau (avec n = 2), (b) rayon, (c) étoile.

Le voisinage géographique auquel nous sommes amenés à penser en premier lieu n'est pas nécessairement pertinent car, d'une part, il s'agirait d'un voisinage trop local, et d'autre part car la socialisation des particules tend à rendre tout voisinage social en voisinage géographique. Enfin, c'est un voisinage très lourd en terme de calculs car nécessitant de recalculer le voisinage de chaque particule à chaque itération [29].

III-4 Formalisation et programmation

La PSO peut facilement être formalisée et programmée. L'espace de recherche est de dimension D. La position courante d'une particule dans cet espace à l'instant t est donnée par un vecteur P_d ( t) , à D

composantes, donc. Sa vitesse courante est V_d ( t) . La meilleure position trouvée jusqu'ici par cette
particule est donnée par un vecteur P_db ( t) . Enfin, la meilleure de celles trouvées par les informatrices de

la particule est indiquée par un vecteur P_dg ( t) . Avec ces notations, les équations de mouvement d'une particule sont, pour chaque dimension d [30]

V ( t ) V ( t - 1 ) .r ( P

= + C - P t

( 1) ) .r ( P

- + C - P t

( 1) )

-

d d 1 1 db d 2 2 dg d

P_d ( t ) = P_d( t -1) + V_d (t)

V_d ( t) : Est la vitesse d'une particule.

P_d ( t) : Est le déplacement d'une particule.

r₁ , r 2 : Sont des nombres aléatoires compris dans l'intervalle [0,1]. C₁ , C ₂: Sont des constantes positives où C₁ + C₂ = 2

III-4.1 Initialisation de l'essaim et Nombre de particules

La position des particules ainsi que leur vitesse initiale doivent être initialisés aléatoirement. Cependant, en ce qui concerne la position des particules, il est préférable d'utiliser un générateur de séquence de SOBOL qui est plus pertinent dans la disposition homogène des particules dans un espace de dimension n. La quantité de particules allouées à la résolution du problème dépend essentiellement de deux paramètres :

· La taille de l'espace de recherche

· Le rapport entre les capacités de calcul de la machine et le temps maximum de recherche.

Il n'y a pas de règle pour déterminer ce paramètre, faire de nombreux essais permet de se doter de l'expérience nécessaire à l'appréhension de ce paramètre.

III-4.2 Coefficient de constriction

Afin d'éviter que les particules ne se déplacent trop rapidement dans l'espace de recherche, passant éventuellement à côté de l'optimum, il peut être nécessaire de fixer une vitesse maximale (notée V max) pour améliorer la convergence de l'algorithme. Cependant, on peut s'en passer si on utilise un coefficient de constriction k et qui permet de resserrer l'hyperespace de recherche. L'équation de la vitesse devient alors :

1 k = - 1 + ( C r C r . + . ) 1 1 2 2		( C r C r + ) ( 2 . . - 4 . C r C r + . ) 1 1 2 2 1 1 2 2
		2

V t

( ) ( ( ) (

= K . V t - 1 + C .r P - P t

( 1) .r P

- +

) (

C - P t

( 1) )

- )

d d 1 1 db d 2 2 dg d

Les études de SHI et EBERHART indiquent que l'utilisation d'un coefficient de constriction donne généralement un meilleur taux de convergence sans avoir à fixer de vitesse maximale. Cependant, dans certains cas, le coefficient de constriction seul ne permet pas la convergence vers la solution optimale pour un nombre d'itérations donné. Pour résoudre ce problème, il peut être intéressant de fixer Vd max = pdmax en plus du coefficient de constriction, ce qui, selon les études de SHI et

EBERHART, permet d'améliorer les performances globales de l'algorithme.

III-4.3 Facteur d'inertie

Le facteur d'inertie w introduit par SHI et EBERHART permet de définir la capacité d'exploration de chaque particule en vue d'améliorer la converge de la méthode. Une grande valeur de w > 1 est synonyme d'une grande amplitude de mouvement et donc, in fine, d'exploration globale. A contrario, une faible valeur de w < 1 est synonyme de faible amplitude de mouvement et donc, d'exploration locale. Fixer ce facteur, revient donc à trouver un compromis entre l'exploration locale et l'exploration globale.

V ( t ) .V ( t - 1 ) .r ( P

= w + C - P t

( 1) ) .r ( P

- + C - P t

( 1) )

-

d k d 1 1 db d 2 2 dg d

w

Où : ( w -

max min )k

w w

= -

k max Kmax

w max = 0.9 Et w min = 0.4 .Donc La taille du facteur d'inertie influence directement la taille de l'hyper

espace exploré. De bons résultats ont été trouvés pour une valeur décroissant linéairement de 0:9 à 0:4 [31].

Pour accélère la convergence de la méthode on peut introduire un autre facteur d'inertie s'appelle Sigmoid qui décroît en fonction du temps.

w k =

w max

- ( w - w ) max min

( ( 1 25 ) )

- -

k

1 exp

+

Où : K est numéro d'itération.

La figure suivante illustre la différence entre le facteur d'inertie linaire et le facteur sigmoid par rapport a la convergence figure III-11.

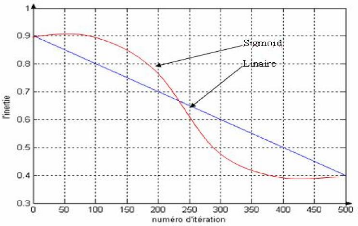
Figure III-11 : Influence d'inertie linéairement et sigmoid

III-5. Algorithmes

Il existe différentes variantes de l'algorithme selon la notion de voisinage que l'on considère, les initialisations de l'essaim, sa taille. L'organigramme suivant expose l'algorithme d'essaim particule ^quirésumés chacune des étapes.

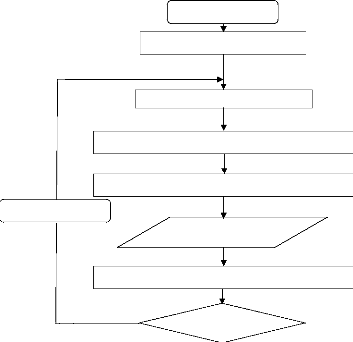
Initiale de population

Evaluation

Calcul de la meilleur fitness de chaque particule

Calcul de la meilleur fitness de population

Début

Nouvelle Population

Terminer

Calcul de la vitesse
Calcul de la position

Début

Résultat

Fin

Figure III-12 : Organigramme d'OEP

III-6 Avantages de L'OEP

L'optimisation par essaim de particules est une méthode d'optimisation itérative stochastique qui s'applique aussi bien aux problèmes à variables continues qu'aux problèmes à variables discrètes, contrairement à d'autres méthodes d'optimisation. De plus, cette méthode permet en général de converge rapidement vers une solution approchée de bonne qualité.

C'est une méthode d'optimisation très largement répandue dont le fonctionnement est relativement simple et qui peut être implémentée très facilement. La version adaptative évite à l'utilisateur d'avoir à fixer les paramètres de l'algorithme comme la taille de l'essaim, les coefficients de confiance c1 et c2 ou le nombre de particules informatrices. A l'initialisation de l'algorithme, il est seulement nécessaire de correctement décrire le problème à optimiser, les contraintes du problème, la fonction coût que l'on veut minimiser [30].

III-7 Conclusion

Dans ce chapitre nous avons tout d'abord présenté quelques généralités sur la méthode d'optimisation génétique et l'optimisation par essaim particule. Ainsi que leurs application pour la résolution de problème de répartition optimale de la puissance électrique.

Malgré le nombre important d'évaluations, les algorithmes stochastiques présentent le grand avantage par rapport aux méthodes déterministes, d'avoir la capacité de trouver l'optimum global. Les méthodes stochastiques les plus prometteuses sont les algorithmes génétiques, les particules d'essaim.

Le chapitre suivant se propose d'appliquer ces méthodes. Elles seront testées et discutées sur des fonctions tests ainsi que pour petits exemples de la répartition optimale de la puissance dans le système électrique.

CHApJETRE IV

Application et Simulation

IV- Application et Simulation :

IV-1 Introduction :

Nous avons assisté ces dernières années à une croissance très rapide des travaux utilisant les techniques métaheuristiques dans les systèmes électriques. Cela est dû à la simplicité de leurs mécanismes, la facilité de leur mise en application et leur efficacité même pour les problèmes complexes. Ce chapitre est consacré au test des algorithmes suivants :

1. Algorithme de l'écoulement de puissance de Newton-Raphson (N-R).

2. Algorithme de l'écoulement de puissance optimale par la méthode lagrangien.

3. Algorithme de l'écoulement de puissance optimale par les méthodes métaheuristiques.

· Algorithme Monte-carlo.

· Algorithme génétique (codage binaire).

· Algorithme d'optimisation par Essaim Particules.

Les tests seront effectués sur des réseaux électriques de petites et moyennes échelles. Ces algorithmes ont été développés dans l'environnement Matlab version 6.5, et exécutés par un microprocesseur Pentium 4 avec 512 MO de RAM et 3 GHZ [02].

IV-2 Optimisation de fonction de coût :

Le problème de ce test consiste à trouver le minimum de la fonction objective suivante :

ng

( ) ( á _i â _i P _Gi ã _i P Gi 2

F x = + + ) (IV-01)

i=1

Chaque puissance active générée P_Gi est limitée par une limite inférieure PGi ( min) est une limite
supérieure PGi ( max) . PGi ( min ) = P_Gi = PGi( max) . Donc la fonction objective est bornée supérieurement, on

va choisir une fonction fitness à maximiser de la forme suivante :

F max

fitness = (IV-02)

F x

( )

Il y a de nombreuses façons de choisie le coefficient F_max . Ce facteur peut être pris comme

coefficient d'entrée, ou bien on peut lui affecter la plus grande valeur de F(x) dans la population actuelle. Nous envisagerons cette dernière possibilité dans cet exemple.

IV-2.1 Test de l'algorithme Génétique :

Dans cette partie, on va appliquer l'algorithme génétique d'optimisation à l'écoulement de puissance, et voir l'avantage de cet algorithme par rapport à celui de l'écoulement de puissance de Newton-Raphson. Ensuite on va procéder à des comparaisons avec la méthode lagrangien et Monte Carlo [29].

Paramètres A-G

Le code représenté par le format binaire est d'une longueur 16 bits pour chaque générateur. Les probabilités de mutation est 0.05 [22]. Le tableau IV-1 montre les paramètres de l'AG utilisés pour cette simulation.

Taille de la population	50-80
La mutation	0.05
Type de croisement	Croisement en un point
Type de sélection	proportionnelle
Nombre de générations	200

Tableau IV-1:.les opérateurs de l'AG - Binaire.

IV-2.2 Réseau test à 6 jeux de barres :

Ce réseau est constitué de 11 lignes de transport, 3 générateurs et 3 charges au niveau des jeux de barres n° 4, 5 et 6 Fig. IV-01. La puissance et la tension de base sont respectivement, 100 MVA et 230 KV [02].

Les coefficients de la fonction quadratique de coût et les limites min et max des puissances actives et réactives des trois générateurs sont donnés dans le tableau IV-2.

		Pgi		Qgi	Coefficients de coût
J-b	limite min.	limite max.	limite min.	limite max.	c	b	a
	(MW)	(MW)	(Mvar)	(Mvar)	($/MW^2hr)	($/MWhr)	($/hr)
1	50.0	200	- 300	300	0.00533	11.669	213.1
2	37.5	150	- 300	300	0.00889	10.333	200.0
3	45.0	180	- 300	300	0.00741	10.833	240.0

Tableau IV- 2 : Les données des fonctions de coût des 3 générateurs du réseau 6 bus

Le niveau de tension de chaque jeu de barre i (en p.u) doit obéir à la contrainte suivante 0 .90 = V_i =1. 1 0

Figure IV-1 : Schéma unifilaire du réseau électrique à 6 jeux de barres

Le tableau IV-3 montre le module et la phase des tensions après la convergence des algorithmes N-R, LAG, MC et A-G on remarque que toutes les tensions sont dans leurs limites admissibles. Les résultats énergétiques et économiques figurent dans le tableau VI-04. Le coût de production de la puissance active, après convergence de l'algorithme génétique est nettement inférieur à celui de l'écoulement de puissance conventionnel N-R (3125.5 $/h contre 3189.5$/h). On peut conclure que l'optimisation des puissances actives nous a permis de réaliser un gain de 64 $/h, et ce en respectant toutes les contraintes de sécurité imposées, sur les tensions, puissances actives et puissances réactives des générateurs.

N° J-B	V ( Pu )				è ( deg ré )
	N-R	Lambda	M-C	A-G	N-R	Lambda	M-C	A-G
1	1.0500	1.0500	1.0500	1.0500	0.0000	0.0000	0.0000	0.0000
2	1.0500	1.0500	1.0500	1.0500	-3.6712	-0.5252	-0.7663	-0.4775
3	1.0700	1.0700	1.0700	1.0700	-4.2733	-0.7809	-0.5621	-0.5662
4	0.9894	0.9870	0.9872	0.9870	-4.1958	-2.1085	-2.2448	-2.0690
5	0.9854	0.9846	0.9846	0.9845	-5.2764	-2.8585	-2.8647	-2.7623
6	1.0044	1.0046	1.0048	1.0047	-5.9475	-2.7278	-2.6687	-2.5773

Tableau VI-3 : Tensions du réseau électrique à 6 J.B.

Il est clair d'après le tableau IV-4 que les pertes de puissance actives ont diminué après l'optimisation. En effet, les pertes par l'algorithme N-R sont de 7.8755 MW, alors qu'ils ne sont que de 6.7406 MW en appliquant l'algorithme génétique, soit une diminution de 1.1349 MW (-14.41%).

N° J-B
	N-R	lambda	M-C	A-G
1 2 3	107.8755 50.0000 60.0000	51.7190 91.0000 74.0000	54.7603 80.2614 81.6568	50.4633 89.117 77.1176
Puissance totale générée	217.8755	216.7090	216.6785	216.6986
Puissance totale demandée	210.0000	210.0000	210.0000	210.0000
Pertes totales de puissance	7.8755	6.7090	6.6785	6.6986
Coût de production ($/h)	3189.5	3126.9	3128.6	3126.4

Tableau IV-4 : Puissances et coûts de production du réseau électrique à 6 J.B.

IV-2.3 Réseau test à 25 jeux de barres :

Ce réseau est classé parmi les réseaux de moyenne échelle et il est constitué de 35 lignes de transport, 5 générateurs et 24 charges Fig. IV-02.

Figure IV-2 : Schéma unifilaire du réseau électrique à 25 jeux de barres

Les limites des puissances générées (en MW et MVAR) ainsi que Les coefficients de la fonction quadratique de coût sont donnés dans le tableau IV-5.

Pgi Qgi Coefficients de coût

J-b	limite min. (MW)	limite max. (MW)	limite min. (Mvar)	limite max. (Mvar)	c ($/MW^2hr)	b ($/MWhr)	a ($/hr)
1	100	300	-150	250	0.0015	1.80	40
2	80	150	-80	150	0.0030	1.70	60
3	80	200	-80	150	0.0012	2.10	100
4	20	100	-80	150	0.0080	2.00	25
5	100	300	-80	150	0.0010	1.90	120

Tableau IV-5 Les données des fonctions de coût des 3 générateurs du réseau 6 bus

D'après le tableau IV-6 on remarque que les tensions avant et après optimisation n'ont pas beaucoup changé, et ils sont dans leurs limites admissibles. Par contre, les phases des tensions ont changé. Cela s'explique par le fort couplage qui existe entre les phases des tensions et les puissances actives.

N° J-B	V ( Pu )			è ( deg ré)
	N-R	lambda	A-G	N-R	lambda	A-G
1	1.0200	1.0200	1.0200	0.0000	0.0000	0.0000
2	1.0000	1.0000	1.0000	13.5558	6.3106	6.4319
3	1.0000	1.0000	1.0000	6.5962	-0.8511	-0.2336
4	1.0000	1.0000	1.0000	2.2322	-3.9781	-1.7422
5	1.0000	1.0000	1.0000	7.4680	1.9193	3.7700
6	0.9802	0.9802	0.9802	7.4548	0.0961	0.4960
7	0.9913	0.9911	0.9922	5.7528	-0.5301	0.1737
8	0.9939	0.9932	0.9942	3.9060	-2.3764	-1.5251
9	1.0026	1.0003	1.0011	2.6911	-2.8173	-1.6411
10	1.0171	1.0154	1.0164	3.3125	-2.0919	-0.6228
11	1.0081	1.0049	1.0063	2.4218	-2.6583	-1.2861
12	0.9929	0.9911	0.9925	3.7334	-1.8661	-0.9112
13	0.9790	0.9791	0.9790	6.5416	-0.8457	-0.3756
14	0.9549	0.9591	0.9589	-2.0256	-5.2563	-4.9869
15	0.9570	0.9606	0.9605	-3.0916	-5.3774	-51861
16	0.9757	0.9758	0.9757	-2.9055	-43782	-4.2545
17	0.9952	0.9907	0.9924	2.5282	-2.2093	-0.9401
18	0.9928	0.9798	0.9845	1.5845	-3.3097	-1.7945
19	1.0094	0.9875	0.9954	2.4203	-2.5995	-0.8340
20	0.9854	0.9860	0.9859	0.4420	-5.1435	-3.1540
21	0.9769	0.9779	0.9779	-0.0611	-4.6233	-3.0375
22	0.9152	0.9755	0.9758	-2.4024	-5.8394	-4.6433
23	0.9983	0.9994	0.9993	-2.2684	-3.4988	-3.0698
24	0.9740	0.9753	0.9752	-5.0039	-7.2144	-6.4429
25	0.9442	0.9781	0.9781	-5.0257	-6.5618	-6.0248

Tableau IV-6 Tensions du réseau électrique à 25 J.B.

Les résultas obtenus par A-G sont comparés avec ceux trouvés par la méthode Newton Raphson et avec la méthode d'optimisation LAG.

N° J-B
	NR	lambda	A-G
1	45.7715	168.5802	142.9237
2	100.0000	94.0000	88.3549
3	150.0000	80.0000	85.1215
4	50.0000	20.0000	32.1059
5	200.0000	181.0000	192.8542
Puissance totale générée	545.7715	543.5802	541.3603
Puissance totale demandée	530.0000	530.0000	530.0000
Pertes totales de puissance	15.7715	13.5802	11.3603
Coût de production ($/h)	1512.50	1472.90	1470.05

Tableau IV-7 Puissances et coûts de production du réseau électrique à 25 J.B.

D'après le tableau VI-7 on peut faire les remarques suivantes

> Toutes les puissances générées sont dans leurs limites admissibles Figure. IV-3.

> Le coût de production de la puissance active a baissé considérablement après convergence de

l'algorithme génétique 1512.50 $/h contre 1470.05 $/h, soit un gain financier de 42.45$/h -2.8%. > En plus du gain financier apporté par l'algorithme génétique de l'optimisation, les pertes totales

de puissance active ont aussi fortement diminuées de 4.4112 MW (-27.96%).

Gén1 Gén2 Gén3 Gén4 Gén5

350

300

Puissance active (MW)

250

200

150

100

50

0

Pgmin Pg Pgmax

Figure IV-3 Puissances actives générées du réseau électrique à 25 jeux de barre.

Le tableau IV-8 donne un résumé sur les résultats obtenus par la méthode génétique ainsi que celles obtenus par les méthodes N-R et LAG [20].

Coût de production ($/h)		Puissance active générée totale (Mvar)			Puissance réactive générée totale (Mvar)		Pertes réactives totales (Mvar)
N-R	1512.50		34,3567	165.0000		-130.6433
LAG	1472.90		23,6492	165.0000		-141.3508
A-G	1470.05		21,8934	165.0000		-143.1066

Tableau IV-8 Comparaison des puissances et coûts de production du réseau électrique à 25 J.B.

On peut dire que les résultats obtenus par la méthode génétique sont meilleurs par rapport aux autres méthodes Figure IV-4.

LAG

A-G

N-R

500 520 540 560 580 600

Puissance active totale Mw Puissance réactive totale Mvar

Pertes actives totales Mw

Figure IV-4 Comparaison des puissances du réseau électrique à 25 jeux de barre.

IV-2.4 Réseau test à 30 jeux de barres (IEEE 30-bus)

Le troisième test est accompli sur un réseau électrique, Constitué de 30 jeux de barres, 41 lignes électriques, 6 générateurs, et 20 charges, puissance demandée pour ce réseau test vaut 283.4 MW [02].

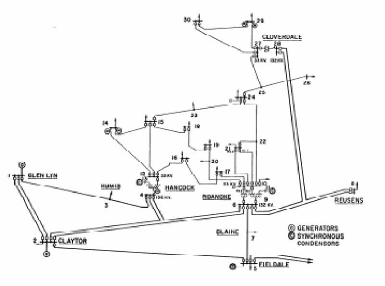
Figure IV-5 : Schéma unifilaire du réseau électrique à 30 jeux de barres.

Les coefficients de la fonction quadratique de coût et les limites min et max des puissances actives et réactives des six générateurs sont donnés dans le tableau IV-9.

	Pgi		Qgi		Coefficients de coût
J-b	limite min. (MW)	limite max. (MW)	limite min. (Mvar)	limite max. (Mvar)	c ($/MW^2hr)	b ($/MWhr)	a ($/hr)
1	50	200	- 20	200	0.00375	2.00	0
2	20	80	- 20	100	0.01750	1.75	0
5	15	50	- 15	80	0.06250	1.00	0
8	10	35	- 15	60	0.00830	3.25	0
11	10	30	- 10	50	0.02500	3.00	0
13	12	40	- 15	60	0.02500	3.00	0

Tableau IV- 9 : Les données des fonctions de coût des 6 générateurs du réseau 30 bus

Convergence de l'Algorithme Génétique :

La figure IV-6 montre les meilleures valeurs sélectives pour chaque génération. Nous remarquons une amélioration de la population est très rapide au début et devient de plus en plus lente à mesure que le temps passe [31]. L'optimum a été obtenu après 156.99 secondes pour les 200 générations. L'influence selon de la taille de la population 50 et 80, nous montre une grande amélioration de la fonction coût avec l'augmentation de la taille de la population, mais elle génère une augmentation du temps d'exécution [22].

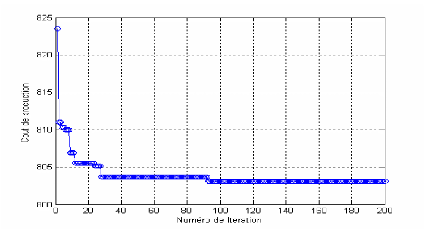
FigureIV-6 : Evolution progressive de la fonction coût de l'AG - Binaire.

IV-2.5 Test de l'algorithme OEP

On va appliquer la méthode d'optimisation par essaim de particules à l'écoulement de puissance, et voir l'avantage de cet algorithme par rapport à celui de l'écoulement de puissance. Ensuite on va procéder à des comparaisons avec la méthode génétique [02].

Paramètres OEP :

L'optimisation par essaims particulaires fournit des solutions proches de la solution optimale à l'aide des mécanismes de modification de vitesse et la position, mais il reste le choix des paramètres de la méthode comme problème principal. Elle est applicable pour nombreux problèmes, dont le problème de l'optimisation de l'écoulement de puissance.

Cinq paramètres rentrent en ligne de compte :

La dimension du problème, le nombre de particules, le type du voisinage, la vitesse maximale et l'inertie. Le tableau IV-10 montre les paramètres de l'OEP utilisés pour cette simulation. [29].

Taille de particules	30-60
l'inertie	Selon l'espace de recherche
Type de voisinage	étoile
Nombre de générations	100

Tableau IV-10 : les paramètres de l'OEP.

Convergence de l'Algorithme ESSAIMS PARTICULES :

Le temps de convergence de l'algorithme OEP a été acceptable, et le processus a convergé à la 71 ème itération. La figure IV-7 montre l'évolution de la fonction coût durant le processus d'optimisation. On voit d'après cette figure que le coût de production commence à partir de la valeur initiale 878.0 $/h, et le passage d'un point de fonctionnement à un autre, jusqu'à l'atteinte du point de fonctionnement optimal qui correspond au coût de production 802.90 $/h

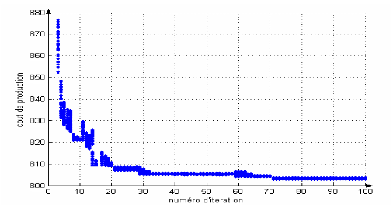
Figure IV-7 : Evolution progressive de la perte par l'OEP.

Il est clair d'après le tableau IV-11 que les contraintes de sécurité pour les modules et phases de tension, sont dans leurs limites admissibles. Aucune tension des jeux de barre de charge, n'a pris une valeur au dessous de la valeur minimum de 0.90 p.u. Fig. VI-8. Les phases des tensions des jeux de barres sont compris entre le minimum de -14.0° et le maximum de 0.0° FigVI-09.

N° J-B	V ( Pu )		è ( deg ré)
	OEP	A-G	OEP	A-G
1	1.0600	1.0600	0.0000	0.0000
2	1.0470	1.0470	-3.8422	-3.8384
3	1.0341	1.0340	-5.7882	-5.7647
4	1.0279	1.0278	-6.9894	-6.9607
5	1.0200	1.0200	-10.6197	-10.4986
6	1.0246	1.0245	-8.0928	-8.0489
7	1.0150	1.0149	-9.6155	-9.5411
8	1.0290	1.0290	-8.4063	-8.3320
9	1.0219	1.0218	-10.2586	-10.3179
10	1.0017	1.0015	-12.1502	-12.1785
11	1.0600	1.0600	-8.9394	-9.1548
12	1.0251	1.0251	-11.6032	-11.6017
13	1.0600	1.0600	-10.7173	-10.7158
14	1.0080	1.0080	-12.5459	-12.5471
15	1.0018	1.0018	-12.5808	-12.5845
16	1.0077	1.0077	-12.1199	-12.1310
17	0.9981	0.9979	-12.3522	-123754
18	0.9891	0.9890	-13.1865	-13.1989
19	0.9848	0.9847	-13.3389	-13.3566
20	0.9882	0.9881	-13.0981	-13.1184
21	0.9590	0.9888	-12.6036	-12.6288
22	0.9894	0.9893	-12.5963	-12.6205
23	0.9874	0.9873	-12.9213	-12.9275
24	0.9767	0.9767	-13.0131	-13.0226
25	0.9808	0.9808	-12.9294	-12.9165
26	0.9624	0.9624	-13.3815	-13.3687
27	0.9923	0.9923	-12.5864	-12.5597
28	1.0211	1.0210	-8.5754	-8.5271
29	0.9717	0.9717	-13.9073	-13.8805
30	0.9599	0.9599	-14.8353	-14.8085

Tableau IV-11 : Tensions du réseau électrique à 30 J.B.

Comme montré dans le tableau IV-12, le coût de production de la puissance active a été réduit de -10.8% après optimisation par l'algorithme OEP, avec un gain financier de 97.7089 $/h. Malgré que les pertes de puissance active ont augmentées après l'optimisation, mais le gain financier reste le plus

significatif.
	N-R	M-C	A-G	OEP
Pg1 (MW)	98.7407	178.0322	178.9512	179.2904
Pg2 (MW)	80.0000	49.8470	45.3800	46.9470
Pg5 (MW)	50.0000	18.0949	22.1800	20.5574
Pg8 (MW)	20.0000	24.5521	24.0600	22.5000
g11 (MW)	20.0000	10.6331	10.4700	11.8750
Pg13 (MW)	20.0000	12.0850	12.0000	12.0011
Pertes de puissances actives (MW)	5.3407	9.8443	9.6412	9.7709
Puissance active générée totale MW)	288.7407	293.2443	293.0412	293.1709
Coût de Génération ($/hr)	900.6128	803.6260	803.1215	802.9039

Tableau VI-12 : Puissances et coûts de production du réseau électrique à 30 J.B.

D'après la convergence des algorithmes d'optimisation OEP on remarque que les tensions avant et après optimisation n'ont pas beaucoup changé. Par ce que une petite variation dans la puissance active au J.d.B, le module de la tension au J.d.B ne varie pas d'une façon appréciable.

[ ] [ ][ ]

Ä Q J ₄ Ä V (IV-03)

Ils sont dans leurs limites admissibles entre 0.90 p.u et 1.10 p.u. Sont d'un minimum de 0.9599 p.u. et d'un maximum de 1.0600 p.u Figure IV-08.

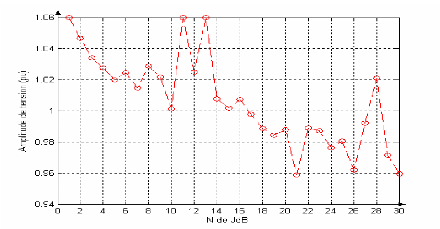
Figure IV-8. Modules des tensions du réseau électrique à 30 jeux de barre.

Par contre, les phases des tensions ont changé. Cela s'explique par le fort couplage qui existe entre les phases des tensions et les puissances actives du système électrique.

[ ] [ ][ ]

Ä P J ₁ Äè (IV-04)

Les angles des tensions sont d'un minimum et d'un maximum de -14.8353° et de 0.0° respectivement Figure IV-04.

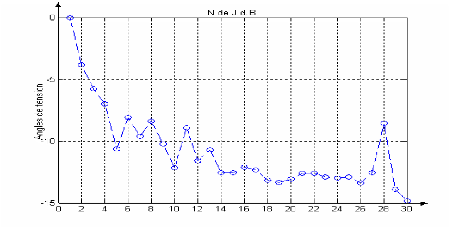
Figure IV-9 : Phases des tensions du réseau électrique à 30 jeux de barre.

IV-3 Optimisation de perte

Pour calculer les pertes dans les lignes, nous partons des équations du Load Flow :

P V G V V G

2

= - i j ( ij ( i

. cos è - è +

j ) ij ( i

G sin è - è _j )

ij i ij

P V G V V G

2

= - i j ( ij ( j

. cos è - è +

i ) ij ( j

G sin è - è _i ) )

ji j ij

La somme de ces termes représente les pertes sur la ligne qui lie les noeuds i et j :

P Lij = P _ij+ P ji

p G V V V

= ij [ i 2 2 _i . _j cos ( i

- è - è +

j ) J 2 ]

V

Lij

p Lij G _ij [ ( V _i V _j ) ² V _i . V _j ( i

- + è - è _j ) ² ]

Ce dernier résultant est obtenu en considérant que è i - è j 0 , on peut donc utiliser le développement en série de Taylor

cos 1 x = -

x

2

2

Si de plus nous faisons l'hypothèse que les tensions aux noeuds sont toutes proches de leur valeur

nominale (1 p.u.), nous obtenons l'approximation :

P

Lij = G _ij è i - è j

( )2

P L = G ij

( - ) ^2 è i è j

Où G = matrice diagonale des conductances de ligne

Le tableau IV-13 expose une comparaison entre les résultats trouvés par les méthodes

d'optimisation AG et OEP. La valeur des pertes de puissances actives dans le réseau test ^trouvépar l'OEP qui est de l'ordre de 4.0841 MW comparée avec celle trouvée par AG qui vaut

4.1193 MW.
	AG-OPF	OEP-OPF
Pg1 (MW)	65.6364	64.5747
Pg2 (MW)	76.4759	75.4726
Pg5 (MW)	47.8127	46.2995
Pg8 (MW)	34.1777	34.6452
Pg11 (MW)	35.8282	39.4744
Pg13 (MW)	27.5884	27.0177
Pertes de puissances actives (MW)	4.1193	4.0841
Puissance active générée totale (MW)	287.5193	287.4841
Coût de Génération ($/hr)	936.4443	936.0629

Tableau IV-13 : Puissances et coûts de production du réseau électrique à 30 J.B.

IV-4 Test sur la fonction multi objective

Maintenant on va tester la méthode d'OEP l'optimisation d'une fonction fortement non linéaire du

coût de combustible pour la production d'énergie électrique et le minimise de perte. La fonction objective est définit comme suit :

( ) ( )

F x

C

F x = (IV-05)

^T P L

L'application a été faite sur le même réseau électrique IEEE 30 bus.

Donc on utilise une fonction plus compliquée (la fonction économique et les pertes active). Les

résultats montre le coût de production, les pertes de puissance active. IV-14 qui suit.	Comme illustrée dans le tableau
	OEP-OPF
Pg1 (MW)	141.6819
Pg2 (MW)	60.3516
Pg5 (MW)	24.1325
Pg8 (MW)	31.2570
Pg11 (MW)	18.3030
Pg13 (MW)	15.5624
Pertes de puissances actives (MW)	7.8884
Puissance active générée totale (MW)	291.2884
Coût de Génération ($/hr)	814.2475

Tableau IV-14 : Puissances et coûts de production du réseau électrique à 30 J.B.

IV-5 Conclusion :

Dans ce chapitre, on a appliqué quelques méthodes métaheuristiques, pour l'optimisation de l'écoulement de puissance, sur des réseaux standard. Les résultats obtenus par l'application de la méthode d'optimisation par particules d'essaims est satisfaisants par rapport à les algorithmes génétiques et très concluants du point de vu coût de production, ainsi que du point de vu pertes de puissances actives qui sont minimisés

CONCLUSION

Conclusion générale

Conclusion et perspectives

L'objective de cette thèse, on a présenté la formulation du problème de la répartition optimale

de puissance dans les réseaux électriques. Les méthodes classiques proposées ont été testées sur des réseaux électriques à moyenne échelle, dont les résultats ont été validés.

La complexité des problèmes liés aux réseaux électriques fait en sorte qu'il est souvent difficile d'utiliser des méthodes classiques, compte tenu du manque de flexibilité dans les cas d'intégrer diverses contraintes spécifiques. Les métaheuristiques constituent alors une stratégie de résolution de plus en plus privilégiée. Une des particularités importantes des métaheuristiques, réside dans l'absence d'hypothèses particulière sur la régularité de la fonction objective. Aucune hypothèse sur la continuité de cette fonction n'est requise, ses dérivées successives ne sont pas nécessaires, ce qui rend très vaste le domaine d'application. L'optimisation par particules d'essaim présente un fort potentiel d'application pratique, par rapport les algorithmes génétiques. Mais le choix de paramètres reste l'un des problèmes de l'optimisation par particules d'essaim, c'est très difficile de trouver des bons paramètres adaptés à la structure du problème.

Deux fonctions simulent dans notre travail. La première calcule la puissance optimale délivrée par chaque générateur avec l'utilisation de la fonction objective simple. La deuxième est multi objective qui introduit l'optimisation des pertes avec la minimise de coût. En perspective, nous proposons d'optimiser d'autres fonctions objectives importantes, comme la puissance réactive et les émissions des gaz toxiques dans l'atmosphère.

ANNEXE

A-1 Réseaux électrique à 6 jeux de barres

Tableau A.1 Données des lignes du réseau électrique à 6 J.B.

Du J.B	Au J.B	r (p.u)	x (p.u)	b/2 (p.u)
1	2	0.10	0.20	0.020
1	4	0.05	0.20	0.020
1	5	0.08	0.30	0.030
2	3	0.05	0.25	0.030
2	4	0.05	0.10	0.010
2	5	0.10	0.30	0.020
2	6	0.07	0.20	0.025
3	5	0.12	0.26	0.025
3	6	0.02	0.10	0.010
4	5	0.20	0.40	0.040
5	6	0.10	0.30	0.030

Tableau A.2 Données des jeux de barres du réseau électrique à 6 J.B.

Numéro	Type	Pd	Qd	V	è	Vmin	Vmax
J.B		(MW)	(MVAR)	(p.u)	(degré)	(p.u)	(p.u)
1	Ref	00.00	00.00	1.05	0.00	0.90	1.10
2	Pv	00.00	00.00	1.05	0.00	0.90	1.10
3	Pv	00.00	00.00	1.07	0.00	0.90	1.10
4	PQ	70.00	70.00	1.00	0.00	0.90	1.10
5	PQ	70.00	70.00	1.00	0.00	0.90	1.10
6	PQ	70.00	70.00	1.00	0.00	0.90	1.10

Tableau A.3 Données des générateurs du réseau électrique à 6 J.B.

Numéro Pg Qg Qmax Qmin Pgmax Pgmin ã â á

J.B (MW) (MVAR) (MVAR (MVAR (MW) (MW) ($/MW2h) ($/MWh) ($/h)

1	00.00	0.0	300.0	-300.0	200.0	50.0	0.00533	11.669	213.1
2	50.00	0.0	300.0	-300.0	150.0	37.5	0.00889	10.333	200.0
3	60.00	0.0	300.0	-300.0	180.0	45.0	0.00741	10.833	240.0

A.2 Réseaux électrique à 25 jeux de barres

Tableau A.4 Données des lignes du réseau électrique à 25 J.B.

Du J.B	Au J.B	r (p.u)	x (p.u)	b/2 (p.u)
1	3	0.0720	0.2876	0.0179
1	16	0.0290	0.1379	0.0337
1	17	0.1012	0.2799	0.0144
1	19	0.1407	0.0097	0.0379
1	23	0.1015	0.2245	0.0873
1	25	0.0759	0.3593	0.0186
2	6	0.0617	0.2935	0.0155
2	7	0.0511	0.2442	0.0175
3	8	0.0579	0.2763	0.0185
3	13	0.0564	0.1478	0.0185
3	14	0.1183	0.3573	0.0113
4	19	0.0196	0.0514	0.0220
4	20	0.0382	0.1007	0.0558
5	21	0.0970	0.2547	0.0057
5	10	0.0497	0.2372	0.1335
5	17	0.0144	0.1269	0.0140
5	19	0.0929	0.2442	0.0140
6	13	0.0263	0.0691	0.0040
7	8	0.0529	0.1465	0.0078
7	12	0.0364	0.1736	0.0110
8	9	0.0387	0.1847	0.0118
9	17	0.0407	0.2075	0.0118
9	10	0.0970	0.2091	0.0900
10	11	0.0890	0.2859	0.0137
11	17	0.1068	0.2807	0.0161
12	17	0.0460	0.2196	0.0139
14	15	0.0281	0.0764	0.0044
15	16	0.0256	0.0673	0.0148
17	18	0.0806	0.2119	0.0122
18	19	0.0872	0.2294	0.0132
20	21	0.0615	0.1613	0.0354
21	22	0.0414	0.1087	0.0238
22	23	0.2250	0.3559	0.0169
22	24	0.0970	0.2595	0.0567
24	25	0.0472	0.1458	0.0317

Tableau A.5 Données des jeux de barres du réseau électrique à 25 J.B.

Numéro J.B	Type	Pd (MW)	Qd (MVAR)	V (p.u)	è (degré)	Vmin (p.u)	Vmax (p.u)
1	Ref	00	00	1.02	0.00	0.90	1.10
2	Pv	10	03	1.00	0.00	0.90	1.10
3	Pv	50	17	1.00	0.00	0.90	1.10
4	Pv	30	10	1.00	0.00	0.90	1.10
5	Pv	25	08	1.00	0.00	0.90	1.10
6	PQ	15	05	1.00	0.00	0.90	1.10
7	PQ	15	05	1.00	0.00	0.90	1.10
8	PQ	25	00	1.00	0.00	0.90	1.10
9	PQ	15	05	1.00	0.00	0.90	1.10
10	PQ	15	05	1.00	0.00	0.90	1.10
11	PQ	05	00	1.00	0.00	0.90	1.10
12	PQ	10	00	1.00	0.00	0.90	1.10
13	PQ	25	08	1.00	0.00	0.90	1.10
14	PQ	20	07	1.00	0.00	0.90	1.10
15	PQ	30	10	1.00	0.00	0.90	1.10
16	PQ	30	10	1.00	0.00	0.90	1.10
17	PQ	60	20	1.00	0.00	0.90	1.10
18	PQ	15	05	1.00	0.00	0.90	1.10
19	PQ	15	05	1.00	0.00	0.90	1.10
20	PQ	25	08	1.00	0.00	0.90	1.10
21	PQ	20	07	1.00	0.00	0.90	1.10
22	PQ	20	07	1.00	0.00	0.90	1.10
23	PQ	15	07	1.00	0.00	0.90	1.10
24	PQ	15	05	1.00	0.00	0.90	1.10
25	PQ	25	08	1.00	0.00	0.90	1.10

Tableau A.6 Données des générateurs du réseau électrique à 25 J.B.

Numéro	Pg	Qg	Qmax	Qmin	Pgmax	Pgmin	ã	â	á
J.B	(MW)	(MVAR)	(MVAR	(MVAR	(MW)	(MW)	($/MW2h)	($/MWh)	($/h)
1	0	0	250	-150	300	100	0.0015	1.80	40
2	100	17	150	-80	150	80	0.0030	1.70	60
3	150	4	150	-80	200	80	0.0012	2.10	100
4	50	-4	150	-80	100	20	0.0080	2.00	25
5	200	-47	150	-80	300	100	0.0010	1.90	120

A.3 Réseaux Electrique à 30 jeux de barres (IEEE 30-bus) Tableau A.7 Données des lignes du réseau électrique à 30 J.B.

Du J.B	Au J.B	r (p.u)	x (p.u)	b/2 (p.u)
1	2	0.02	0.06	0.03
1	3	0.05	0.19	0.02
2	4	0.06	0.17	0.02
3	4	0.01	0.04	0.00
2	5	0.05	0.20	0.02
2	6	0.06	0.18	0.02
4	6	0.01	0.04	0.00
5	7	0.05	0.12	0.01
6	7	0.03	0.08	0.01
6	8	0.01	0.04	0.00
6	9	0.00	0.21	0.00
6	10	0.00	0.56	0.00
9	11	0.00	0.21	0.00
9	10	0.00	0.11	0.00
4	12	0.00	0.26	0.00
12	13	0.00	0.14	0.00
12	14	0.12	0.26	0.00
12	15	0.07	0.13	0.00
12	16	0.09	0.20	0.00
14	15	0.22	0.20	0.00
16	17	0.08	0.19	0.00
15	18	0.11	0.22	0.00
18	19	0.06	0.13	0.00
19	20	0.03	0.07	0.00
10	20	0.09	0.21	0.00
10	17	0.03	0.08	0.00
10	21	0.03	0.07	0.00
10	22	0.07	0.15	0.00
21	22	0.01	0.02	0.00
15	23	0.10	0.20	0.00
22	24	0.12	0.18	0.00
23	24	0.13	0.27	0.00
24	25	0.19	0.33	0.00
25	26	0.25	0.38	0.00
25	27	0.11	0.21	0.00
28	27	0.00	0.40	0.00
27	29	0.22	0.42	0.00
27	30	0.32	0.60	0.00
29	30	0.24	0.45	0.00
8	28	0.06	0.20	0.02
6	28	0.02	0.06	0.01

Tableau A.8 Données des jeux de barres du réseau électrique à 30 J.B.

Numéro J.B	Type	Pd (MW)	Qd (MVAR)	V (p.u)	è (degré)	Vmin (p.u)	Vmax (p.u)
1	Ref	0.0	0.0	1.060	0.00	0.90	1.10
2	Pv	21.70	12.7	1.043	0.00	0.90	1.10
3	PQ	2.4	1.2	1.000	0.00	0.90	1.10
4	PQ	7.6	1.6	1.000	0.00	0.90	1.10
5	Pv	94.2	19.0	1.010	0.00	0.90	1.10
6	PQ	0.0	0.0	1.000	0.00	0.90	1.10
7	PQ	22.8	10.9	1.000	0.00	0.90	1.10
8	Pv	30.0	30.0	1.010	0.00	0.90	1.10
9	PQ	0.0	0.0	1.000	0.00	0.90	1.10
10	PQ	5.8	2.0	1.000	0.00	0.90	1.10
11	Pv	0.0	0.0	1.082	0.00	0.90	1.10
12	PQ	11.2	7.5	1.000	0.00	0.90	1.10
13	Pv	0.0	0.0	1.071	0.00	0.90	1.10
14	PQ	6.2	1.6	1.000	0.00	0.90	1.10
15	PQ	8.2	2.5	1.000	0.00	0.90	1.10
16	PQ	3.5	1.8	1.000	0.00	0.90	1.10
17	PQ	9.0	5.8	1.000	0.00	0.90	1.10
18	PQ	3.2	0.9	1.000	0.00	0.90	1.10
19	PQ	9.5	3.4	1.000	0.00	0.90	1.10
20	PQ	2.2	0.7	1.000	0.00	0.90	1.10
21	PQ	17.5	11.2	1.000	0.00	0.90	1.10
22	PQ	0.0	0.0	1.000	0.00	0.90	1.10
23	PQ	3.2	1.6	1.000	0.00	0.90	1.10
24	PQ	8.7	6.7	1.000	0.00	0.90	1.10
25	PQ	0.0	0.0	1.000	0.00	0.90	1.10
26	PQ	3.5	2.3	1.000	0.00	0.90	1.10
27	PQ	0.0	0.0	1.000	0.00	0.90	1.10
28	PQ	0.0	0.0	1.000	0.00	0.90	1.10
29	PQ	2.4	0.9	1.000	0.00	0.90	1.10
30	PQ	10.6	1.9	1.000	0.00	0.90	1.10

Tableau A.9 Données des générateurs du réseau électrique à 30 J.B.

Numéro J.B	Pg (MW)	Qg (MVAR)	Qmax (MVAR	Qmin (MVAR	Pgmax (MW)	Pgmin (MW)	ã ($/MW2h)	â ($/MWh)	á ($/h)
1	0	0.000	200	-20	200	50	0.00375	2.00	0
2	80	27.687	100	-20	80	20	0.01750	1.75	0
3	50	21.544	80	-15	50	15	0.06250	1.00	0
4	20	22.933	60	-15	35	10	0.00830	3.25	0
5	20	38.883	50	-10	30	10	0.0250	3.00	0
6	20	40.345	60	-15	40	12	0.0250	3.00	0

Bibliographies

[1]: Delendi Louardi, " Controle de l'écoulement de puissance active par FACTS", Mémoire de Magister, Université de Batna, 2009.

[2]: S. Sayah, "Application des ensembles flous a la repartition optimale de la puissance dans les reseaux electriques " Mémoire de Magister, Université de Sétif, 2005

[3]: W.D. Stevenson, "Elements of Power System Analysis", New York, NY: McGraw Hill, Inc, 1994.

[4]: HAIMOUR Rachida , " Contrôle des Puissances Réactives et des Tensions par les Dispositifs FACTS dans un Réseau Electrique " Mémoire de Magister, Université d'Oran, 2009

[5]: K.Chikhi, "Contribution a l'analyse de la qualite de l'énergie électrique dans la cas de la stabilite de la tension" Mémoire de Doctorat , Université de Batna, 2007

[6]: Computer methods in power system analysis (chapter 08), ALLEN W.stagg, Ahmed H ELAbier, International Student Edition

[7]: Gasbaoui B," Optimisation de l'énergie réactive dans un réseau d'énergie électrique" Mémoire de Magister, Centre Universitaire de Béchar

[8]: Prabha Kundur, « Power system satability and control», EPRI, 1993

[9]: A.Messaoudi "Dispatching économique des réseaux électriques par les methods numériques " Mémoire de Magister, Université de Batna, 2001

[10]: Theodore Wildi "Electrotechnique" Presse de l'Université de Laval, Canada, 1978

[11]: Olle I.Elgerd" Electrique energy system teory introduction" Mc Graw-Hill, 1982

[12]: A.J. Wood & B.F. Wollenberg, "Power Generation Operation and Control", New York, NY, John Wiley & Sons, Inc, 1984, pp. 39,517.

[13]: A.Ponsich,"Strategies d'optimisation mixte en genie des procedes application a la concepation d'ateliers discontinues"Mémoire de Doctorat, institute national polytechnique de Toulouse2005

[14]: Alain Berro, "Optimisation multiobjectif et stratégies d'evolution en environnement dynamique" Mémoire de Doctorat, Université de Toulouse I, 2001

[15]: H.Omessaad"Contribution au devloppement de méthods d'optimisation stochastique. Application a la concepation des dispositif electrotechniques" Mémoire de Doctorat, Ecole central de lille, 2003

[16]: R.R.Saldanha "Optimisation en électromagnétisme par application conjointe des méthodes de programmation nom linéaire et de la méthode des elements finis" Thése de doctorat, Institut national Polytechnique de grenoble, 1992

[17]: F.Médioni"Méthodes d'optimistion pour l'évitement aérien système centralises, systèmes embarqués" Mémoire de Doctorat, Ecole polytechnique, 1998

[18]: Nicolas Durand "Algorithmes génétiqueset autres outils d'optimisation appliqués à la gestion de trafic aérien",2004

[19]: Ludovic, Mé., Audit de sécurité par algorithmes génétiques. Thèse de Doctorat, Université de Rennes 1, France, 7 Juillet 1994.

[20]: M. Nasri et M. EL Hitmy"Algorithme Génétique et Critère de la Trace pour l'Optimisation du Vecteur Attribut : Application à la Classification Supervisée des Images de Textures" Maroc

[21] J.M.Alliot, T.Schiex "Intelligence Artificielle et informatique Téorique" Cepadués-Edition, Toulouse, pp, 441-460,1994

[22] Mimoun Y, M RAHLI, M. KANDOUCI "Répartition économique des puissance par un algorithme génétique en code réel Application a un réseau 118 noeuds " Conférence,2006, Maroc

[23] Adrian Rafael DIETZ" Optimisation multicritère pour la conception d'ateliers discontinus multiproduits :aspects économique et environnemental" Mémoire de Doctorat, , institute national polytechnique de Toulouse 2004

[24] Souquet Amédée et Radet Francois-Gérard "Algorithmes génétiques"TE de fin d'année,2004

[25] Atousa ASSADI-HAGHI"Contribution au développement de méthodes d'optimisation structurelle pour la conception assistée par ordinateur de composants et de circuits hyperfréquences" Mémoire de Doctorat, Université de Limoges, 2007

[26] Bruno SARENI" Méthodes d'optimisation multimodales associees a la modelisation numérique en electromagnétique" Mémoire de Doctorat, L'ecole centrale de Lyon,1999

[27] R. Duvigneau, "Introduction aux Méthodes d'Optimisation sans Gradient pour l'Optimisation et le Contrôle en Mécanique des Fluides"2006

[28] OUADFEL SALIMA" Contributions à la Segmentation d'images basées sur la résolution collective par colonies de fourmis artificielles" Mémoire de Doctorat, Université de Batna, 2006

[29] Antoine Dutot et Damien Olivier"Optimisation par essaim de particules Application au problème des n-Reines"

[30] Guillaume CALAS"Optimisation par essaim de particules" France,

[31] V.Magnin, enseignant-chercheur " Optimisation et algorithms génétique"