Contribution à la détermination des paramètres ultrasonores des gondolements des fibres dans un matériau composite à matrice céramique renforcé des fibres du «rhectophyllum camerunense

Chapitre II : PROPAGATION DES ONDES ULTRASONORES

2.1. INTRODUCTION

L'étude de la propagation des ondes ultrasonores dans les solides nécessite la connaissance de la structure de l'onde et des propriétés du milieu de propagation [5]. Dans la suite de cette étude, l'onde supposée plane, progressive et monochromatique, se propage dans un milieu élastique, anisotrope et homogène par rapport aux longueurs d'ondes considérées.

2.2. ÉQUATION DE PROPAGATION

Fig. 2.1 : Surpression d'un gaz dans un piston en mouvement

Hypothèses :

.Gaz traité comme un milieu continu : particule fluide grand nombre de particules

microscopiques

· Pression P0 à l'équilibre

· Problème unidirectionnel : la pression introduite par le mouvement du piston est de la forme 6p(x, t).

2.2.1 Expression du champ de surpression

La variation de 6(dfl) du volume dfl de la tranche est initialement comprise entre x et x + dx. u(x, t) est le déplacement à l'abscisse x.

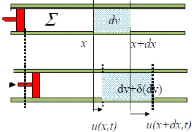
Fig.2.2 : variation du volume d'une tranche de fluide

MEMOIRE DE MASTER II RECHERCHE 11 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

S(d?) = ?[u(x + dx) -- u(x)1 (2.1)

Or u(x + dx) '' u(x) + ~~~

~~~ dx (2.2)

S(~?) ,,, ? (au

~~) _dx 8(c?) ~? ~ ~~ ~~~

~~~ (2.3)

Alors

8(c?) (2.4)

Et =

d?

S est la dilatation de la tranche fluide. C'est une des grandeurs propagée par l'onde.

_Sp = _k 8(d") ~" ~ ~~ ~~~

~~~ (2.5)

est l'équation de couplage entre les champs de surpression et de déplacement propagés par l'onde. 2.2.2 Équation fondamentale de la dynamique

On suit le mouvement d'une masse constante dm de gaz, initialement comprise entre deux sections d'abscisse x et x + dx.

Position à t de la tranche en x au repos : x + u(x, t).

Position à t de la tranche en x + dx au repos : x + dx + u(x + dx, t)

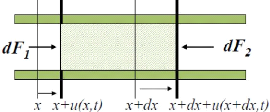
Fig. 2.3 : mouvement d'une masse constante de gaz

Force résultante sur la tranche :

dF = dF1 + dF2 = ?[P0 + Sp(x + u(x)) -- (1³0 + Sp(x + dx + u(x + dx)))] (2.6)

dF = ? .9x ^asP (1 + ~~

_ax) dx (2.7)

Approximation acoustique : ~~

~~ <<< 1 = amplitude de vibration des particules <<< 2.

~$ + ? ~~,

~~ ~~ ~ ~# 0

10 ~ 2(?~~ 0

10 on obtient par la suite, (2.8)

3⁴5

364 = 78₉ 3⁴5

3:4: Équation d'onde [5] (2.9)

Remarque :

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Soit u(x, t) le champ scalaire de déplacement d'une particule fluide.
· Cas d'un milieu parfait illimité :

{ AO -- k ^a25., 0
^P =

Po at^-

(2.10)

Po at²

k a2ri

= 0

Art --

Cette équation qui vérifie à la fois le champ de surpression, le champ de déplacement, la vitesse de particules et la dilatation est appelée Équation d'Alembert [6]

En prenant l'expression suivante :

a²sp

at²

= 0

k

A8p --

Po

On remarque que la constante k

s'exprime en (ms^--1)^-2 ; l'équation précédente s'écrit :

= 0 (2.11)

Po

1

A8p --

_C2

a²sp
at²

MEMOIRE DE MASTER II RECHERCHE 12 2008-2009

où la constante c a les dimensions d'une vitesse.

2.2.3 Solutions progressives dans un milieu illimité 1D

Recherchons s'il existe des solutions de l'équation d'Alembert sous forme d'ondes progressives, telles que nous les avons définies plus tôt. Pour le champ de surpression nous supposons une fonction telle que :

8p(x, t) = f(a(x, t)) + ^9(f3(x, t)) (2.12)

x Avec a(x, t) = t -- v

; f3(x, t) = t +^x v

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

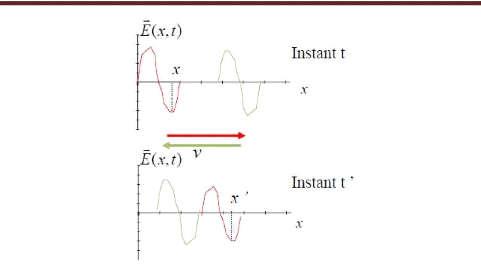
Fig. 2.4 : ondes progressives et régressives

Ici, V représente la vitesse de propagation des ondes progressives dans le milieu.

.

a²6p(x,t)

at²

a²6p(x,t) 1

ax^{2 ~}v²

= 0 (2.15)

aSp(x,t)

aa(x,t)

=

aSp(x,t)

ax

^df-I-

af3(x,t)

ax da ax

aSp(x,t)
ax

df1

-I-
da v

dg

(2.13)

df3

aa(x,t)

=

^df-I-

af3(x,t)

at da at

aSp(x,t)
ax

dg

-I- df3 (2.14)

dP

df

=

at

dg
df3

.

1
v

=

dg
df3

.

MEMOIRE DE MASTER II RECHERCHE 13 2008-2009

Les ondes progressives sont solution de l'équation d'Alembert, dans laquelle intervient la constante V.

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.2.4. Vitesse de propagation et propriétés du milieu

La vitesse de propagation des ondes élastiques est directement liée aux propriétés du matériau.

v= .\I = Po

(2.16)

Cette relation peut être exploitée :

· Pour évaluer la distance dans un milieu connu par mesure d'un temps de propagation ;

· Pour évaluer les modules de compression par mesure de la vitesse de propagation.

2.2.5. Notion d'impédance

Soit une OPP se propageant dans le sens des x croissants (respectivement décroissants) :

a87(x, t) = f (t #177; x) (2.17)

a6p(x,t)

at

=f

O JZ[ . X ~,~

X ~ YO X ~,~

a6p(x,t)

ax

X (2.18)

~ Y 1

·

= W>? = ~ ^2( ~ 2(O

(2.22)

Z_C =

V

k

MEMOIRE DE MASTER II RECHERCHE 14 2008-2009

Équation d'état du fluide X ~, ~~ ~ ~~ ~~~,1

~~ . ~~,~,1

1 ~ ~~ ~~\ ~,1

~~ (2.19)

Donc : +a 6p(x, 0 V 36

= k35\ (x,t) (2.20) 36

Soit en intégrant, aop(x, t) = +:

it(x, t) = Zii(x, t) (2.21)

Avec Z = + k v

= +;

On note que Z_c ne dépend que des propriétés du milieu.

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.3. RÉGIME D'ONDES PLANES DANS LES SOLIDES ANISOTROPES ILLIMITÉS

2.3.1. Modèle tridimensionnel

Le volume balayé par d? lors du déplacement :

d? = uA^B . d?

--) = u.1

d? (2.23)

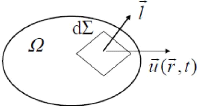
Fig. 2.5 : représentation d'un volume balayé lors du déplacement Variation totale de volume :

?(?) = I?it⁾ .`^B d? = i_?diV(11)d? = i_? (i^B)C? (2.24)

(i⁾-) = div (1)

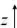
MEMOIRE DE MASTER II RECHERCHE 15 2008-2009

	a^2.A^B		AAAAAAAAB			Po
			(op) (2.27)

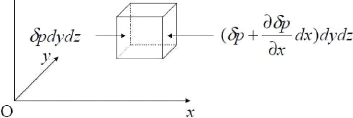
Fig. 2.6 : représentation de la variation totale de volume

sp a

F_x = Spdydz -- (Sp + _aax dx) dydz = _ax^e dxdydz (2.25)

aux asp 2(~e~f 10 ~ ~ ~~~e~f . 2( 0g

10 ~ ~ ~~,

~~ (2.26)

~~

Compte tenu des relations identiques sur les axes y et z, l'équation fondamentale de la dynamique devient :

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

En prenant la divergence des deux membres,

Po	a2div(u) B		= --div (grci(Sp)) = --?(8P) (2.28)

Prenons en compte la relation de compressibilité du milieu qui s'écrit maintenant :

sp .k 5(c?) ~? ~ ~~ ~d^B ~ ~~~cO~~~^AB (2.29)

a20 _k

Il vient que : = ?(8p) (2.30)

a1 0 Po

2.3.2. Flux de puissance - Vecteur de Poynting

En présence d'une densité de force appliquée, la loi fondamentale de la dynamique s'écrit :

Po

a2ri a1^0 = Po

dit dt

AAAAAAAA^B = --grad

(^8p) +f

(2.31)

= (fu) = ^d_t (e_c + ep) + div(P) (2.39)

d

^B

dw

.

dt

=f

dil
dt

MEMOIRE DE MASTER II RECHERCHE 16 2008-2009

Et le travail des forces appliquées au cours du déplacement

-, dw = f

. dit (2.32)

AAAAAAAA^B dw = grad Avec A^B ~ \^AB

- (SP) . dil + Po^dd^ut^. d

. dif (2.33)

AAAAAAAA^B . dw = grad Or

(Sp) . dil + Poll

-) . dit

(2.34)

AAAAAAAA^B grad

(Sp) . &it = div(Sp . dif) -- Spdiv(dif) (2.35)

Et

div(dif) = d (i²) (2.36)

.dw = div(Sp ii) -- Sp. d ^B + d(¹₂ poiI²) (2.37)

d C port²) = de_c : Variation de la densité volumique d'énergie potentielle Sp. d ^B ~ de_p : Variation de la densité volumique d'énergie cinétique.

-) On définit le vecteur de Poynting par : P D'où :

-) = Spit

(2.38)

MEMOIRE DE MASTER II RECHERCHE 17 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

En intégrant sur tout le volume ? ,on obtient :

dW
dt

mo (E' + E) + ff?p-) d?AAAAAA) (2.40)

m

Avec :

mn : Puissance fournie par les sources internes au volume

mo

mo (E + E_~):Puissance stockée sous forme d'énergie cinétique et potentielle

m

a?'^AB d?^AAAAAB: Puissance rayonnée vers l'extérieur.

Le vecteur de Poynting représente en direction et en amplitude la densité par unité de surface de puissance rayonnée vers l'extérieur d'un volume.

La puissance rayonnée est égale au flux du vecteur de Poynting à travers la surface limitant le volume ?.

On définit l'intensité comme la moyenne dans le temps du vecteur de Poynting, soit :

I =< P(t) >= limTxy w f 8p(t)~\ (t)

w

G dt [5] (2.41)

(

2.4. PROPAGATION DES ONDES PLANES PROGRESSIVES EN 3D

o Une onde plane progressive est une onde plane propage qui se dans une direction et un sens bien définis.

o L'onde plane est définie par la direction dans laquelle elle se propage.

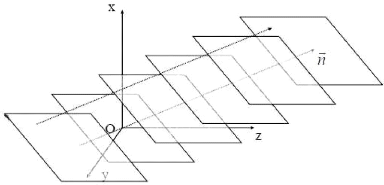
Fig. 2.7 : représentation de la direction de propagation des O.P.P. en 3D

= x .0(¹, t) = ⁸7³1 (t -- ^~_x) (2.47)

^B

-) -)

-)

.r

n = e_x; n

MEMOIRE DE MASTER II RECHERCHE 18 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.4.1. Expression analytique des O. P. P.

On peut facilement déduire l'expression d'une onde plane progressive du schéma ci-dessous :

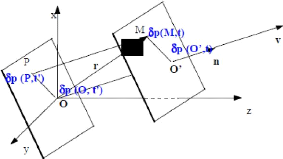
Fig. 2.8 : Schéma de propagation d'une O.P.P suivant les axes

613(I K, t) = 613(01,t) (2.42)

613(0, t^') = 613(', t^') = 6131(t') (2.43)

Avec

t = t' +^"1 v

t' = t ^PM v

ii . i-' = t i;

(2.44)

En posant : il' = OM B

81(M, t) = 81(P, C) = 0(⁰,0 (2.45)

.8W-, t') = Sp (0, t AB . ...B

" ~ = 8p1(t AB . ...B

" ~ (2.46)

· Cas particulier d'une onde se propageant suivant Ox

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.5. PROPAGATION DES ONDES PLANES ET ÉTAT DES CONTRAINTES

2.5.1. Déformations

Il ya déformation si le gradient des déplacements est non nul mais ne s'annule pas pour une rotation d'ensemble.

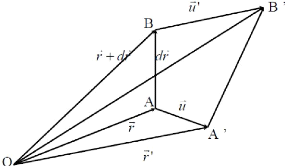
Fig. 2.9 : schéma d'illustration d'une déformation

~A^B}= A^B

(1^2 + di^)-) (2.48)

~^}i)~‡ ~~~‡* ~ ~i)~‡* ~ ~~à

~~%o UXi = Ui(Xj) + dui (2.49)

~d^B}= aldf=i -- dr = (al -- ~i‡*~d^B‡ (Rotation infinitésimale) (2.50)

1 yo 0 0 yo 0

Avec Ki ‡ ~ ~ 1 0 OE ~~à

~~%o ~ )Ki ‡ ~ ~i‡* ~ ~ 0 0 OE (2.51)

0 0 1 0 0 0

Èéè ~ F G '~~à

~~à ~ Èéè ~ i‡ ê

~~%o ~ ~~%o

~~à« ; h†~cDe#é~dcï~k

(2.52)

~~%o i‡ ~ F G '~~à

~~%o ~ ~~%o

~~à« ; De#é~dcï~k

MEMOIRE DE MASTER II RECHERCHE 19 2008-2009

Seule la partie symétrique s'annule pour tout mouvement d'ensemble. Donc seul ij (tenseur des déformations) représente une variable de déformation.

Pour résumer :u; = ui ~ ÈéèdXi + iidXi (2.53)

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

La dilatation s'exprime par :

A^B = div(u)

~

aui axi

= ii = 11 + 22 + 33 (2.54)

MEMOIRE DE MASTER II RECHERCHE 20 2008-2009

2.5.2. Contraintes

^AB)`^B* = (dFe-->i) mdE-> 0 dE

(2.55)

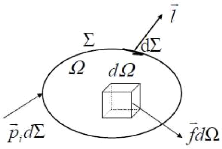
Fig. 2.10 : volume représentatif

Fi = i_ETAdÓ + 1?fid? = 0 (2.56)

Théorème de Green fi = ^aTik (2.57)

axk

Avec : Ti(t) = Tiklk

2.5.3. Équation du champ : équilibre statique - dynamique

aTik

+ = 0 (2.58)

oxk

En l'absence des forces volumiques, on a :

aTLi

~ 0 (2.59)

~~oe

Fi = iETKNÓ + i_?Ji~? = 1?~Xc~ _X~+ f₁)d? (2.60)

pù$ú at

²ⁱ 2 -- + f. (2.61)

at ₂- aT axk.k

Avec : Ti(t) = Tiklk

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.5.4. Loi de comportement linéaire d'un solide élastique Hypothèse des petites déformations :

raTo f a²Ti;

kI ,,, + ...(6) (2.62)

Tik(Skt) = Tik(Skt = 0) + ) kl

2 .
·9.SkiaS_nini Sia=⁰ --

Smn=⁰

ask' _sia=0

Soit Tik( ki) = Cijki ki (2.63)

Avec §i‡=· ~ ~~wà%o

~ oe~ oecents( (2.64)

· Équation de propagation

La prise en compte de la loi de Hooke dans la loi fondamentale de la dynamique conduit à : Hypothèse : les forces de pesanteur de densité volumique f sont négligeables.

2 X2~c

X2 ~ ~wà%o X2`

~~%o (c) 2 X2~c

X2 ~ §c·` X·X~ (2.65)

c· ~ §c·` <sup>X`</sup> axk

2.5.5. Régime d'ondes planes dans les solides anisotropes illimités

~i ~ i. $ ~~ ~ A^B . ...^B

« ~ ~ i. $ ~~ ~ %o . ...%o

« ~ (2.66)

a2u1 X2 ~ c. $

<=

®

I,

#172;

02111 = U`. ^njn2 ^k F ax.aXk

pUi. F

_njnk

= C ijklU I. 2 P (2.67)

~ nj

1. _v P

II_;

au,

ax.

MEMOIRE DE MASTER II RECHERCHE 21 2008-2009

pV²Ui = Cijki ?link U1 : Equation de Christoffel [7] (2.68)

Signification de l'Equation de Christoffel

PV²Ui = Ct_./id njnk U1

En posant : ll = Cum nink (2.67)

Il vient que : ll u1 = pV²Ui (2.68)

La polarisation U1 est un vecteur propre du tenseur ii avec pour valeur propre pV².

MEMOIRE DE MASTER II RECHERCHE 22 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

NB : Le tenseur de Christoffel étant symétrique, ses valeurs propres sont réelles et positives et ses vecteurs propres orthogonaux.

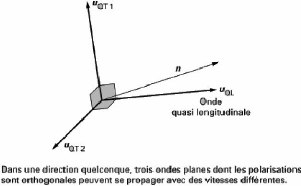
Fig 2.11 : Propagation des ondes [2]

2.6. PROPAGATION DES ONDES PLANES DANS LES MILIEUX ISOTROPES
ILLIMITES

Dans une direction donnée n d'un solide isotrope, peuvent se propager une onde plane longitudinale et une onde plane transversale.

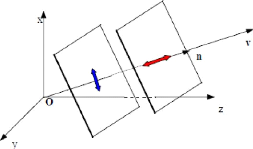
Fig 2.12 : Propagation des ondes planes dans les milieux isotropes

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Les vitesses de propagation respective de l'onde longitudinale 17_/, et de l'onde transversale VT sont données par :

VL ~ W'Fu

> (2.69)

VT = .\11.1 > (2.70)

2.7. Vitesse d'énergie

Par définition, le vecteur « vitesse d'énergie » est égal au quotient du vecteur de Poynting par la densité volumique d'énergie : [5]

~~à

1 ~ i J}

Si ~i ~ i J ~~ ~ %o ~%o

« ~ ; (2.71)

~~%o ~ %o

~~à « i J}

F

G 2 ~ ~0~à ~ F G 2 i FJ}F

10 ~

e_c =

(2.72)

MEMOIRE DE MASTER II RECHERCHE 23 2008-2009

e_P =

1 2

§i‡=· i‡ =· ~ F G §i‡=· ~~à ~~%o ~~ ~~oe ~ F G §i‡=· †‡†= à «0 J}F (2.73)

Christoffel donne :

Ciiki nink UL Ul = 2 V2Ui2 (2.74)

te e, =

G 2 i F J}F ~ kH (2.75) F

e = 2 Ui² f'² (2.76)

~~%o ~~ ~~%o

'i ~ ~i‡ ~ ~§i‡=· 'i ~ ~§i‡=· ‡ · oe « J}F (2.77)

1 ~~oe 1

_v Cijkl U j Ulnk ·

= ; en choisissant UL = 1 (2.78)

PV

La vitesse d'énergie indique (comme le vecteur de Poynting) la direction du transport de l'énergie c'est-à- dire la direction du « rayon acoustique ». [8]

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

On parle de mode de propagation pur quand le rayon est perpendiculaire au plan d'onde. Pour une direction de propagation donnée, formons le produit scalaire

O^B·. †A^B = vi ·. n = Ctjkl ^U) Ulnknt ; or _{CjjktfljflkUj} U1 = 2 V² Ui F (2.79)

> à 0 «

O^Be. †A^B _. V (2.80)

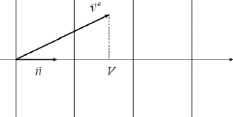
Fig 2.13 : projection de la vitesse d'énergie sur la direction de propagation

La projection de la vitesse d'énergie sur la direction de propagation est égale à la vitesse de

phase.

· Surfaces caractéristiques - Surface des vitesses

Lieu de l'extrémité du vecteur vitesse de propagation, tracé à partir d'une origine O, lorsque la direction de propagation varie.

Un solide anisotrope est alors décrit par une surface des vitesses constituée de trois nappes (une pour l'onde quasi-longitudinale et une pour chacune des ondes quasi-transversales.)

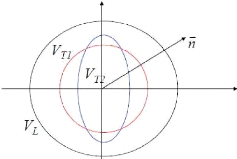
MEMOIRE DE MASTER II RECHERCHE 24 2008-2009

Fig. 2.14 : allure schématique du lieu de l'extrémité du vecteur vitesse de propagation [9]

MEMOIRE DE MASTER II RECHERCHE 25 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

2.8. Phénomènes de réflexion / transmission (régime d'ondes planes et milieux isotropes)

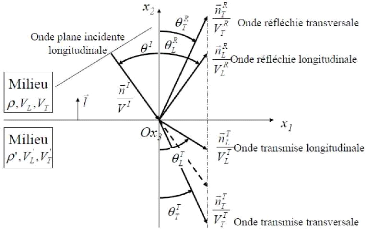
Fig. 2.15 : illustration du phénomène de réflexion/transmission [10]

· Conditions aux limites

fliⁱi (X2 = 0) + ? ~i ½ ~~F ~ 0 ~ ? ~i ^w ~~F ~ 0 ; c ~ 1,2,3

½ w

(2.81)

Ti (x2 = ⁰) + ? i ½ ~~F ~ 0 ~ ? i ^w ~~F ~ 0 ; c ~ 1,2,3

½ w

¼ J¼ ~~ ~ AB....B

~i ¼ ~ i « ~ (2.82)

Conséquences des conditions aux limites

En i= = 0A^B

,

Ui ¼ f^I(t) + ? R Ur fR = ? T ut f^T(0; t = 1,2,3 ; V t (2.83)

f^l(t) = f(t) = f^R(t) (2.84)

Toutes les ondes sont de même forme temporelle. Pour les ondes harmoniques, cela signifie que toutes les ondes en presence ont la même fréquence.

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

En r= i.>p,

w J '~ ~ ABÄ....ÂAB

i ¼ J '~ ~ AB....ÂAB

« « ~ ? i ½ J '~ ~ AB....ÂAB

« « ~ ? i 1,2,3 ; À ~ (2.85)

½ w «Ä « ; c ~

nA^Br.r_~A^B

nA^BÁ.d_~A^B

~

V^I

V^R

~ nAB.r~AB

(2.86)

V^T

~A^B

« ~ AB _vi) . r_p^-

= 0

; (2.87)

~A^BÄ

«Ä ~ AB

«~ . d^B, = 0

· Interprétation géométrique

_triR _fit

\

vR vI) . r_p = 0 (2.88)

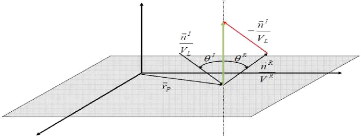
Fig 2.16 : interprétation géométrique 1

Fe est contenu dans le plan défini par la normale et 71.^1/4

₍._FiT .₇₁1₎ it 0

_vT _VI p = (2.89)

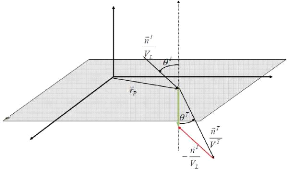
MEMOIRE DE MASTER II RECHERCHE 26 2008-2009

Fig 2.17 : interprétation géométrique 2

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

--)T --)I

n est contenu dans le plan défini par la normale et n

· Loi de Snell - Descartes : interprétation géométrique

~A^B

« ~ AB ÅéÆ Ç

« ~ ÅéÆ Ç

«~ . d^B, ~ 0 «

; ; (2.90)

~A^BÄ

«Ä ~ AB ÅéÆ ÇÄ

v¹

«Ä ~ ÅéÆ Ç

«~ . d^B, ~ 0

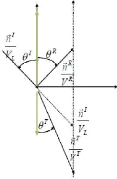
MEMOIRE DE MASTER II RECHERCHE 27 2008-2009

Fig 2.18 : présentation des vecteurs lenteurs sur la surface

'x fi_x ^x

Tous les vecteurs lenteurs = ont la même projection sur la surface.

v

· Angles critiques et courbes des lenteurs

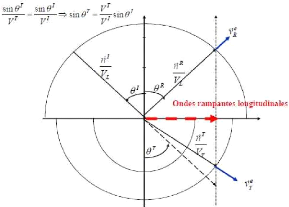
Fig 2.19 : allure schématique des angles critiques et courbes des lenteurs [11 ]

DEUXIEME PARTIE : APPLICATION A LA
CARACTERISATION DES PARAMETRES ULTRASONORES
DE DETECION DES GONDOLEMENTS DES FIBRES DANS
UN MATERIAU COMPOSITE

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

MEMOIRE DE MASTER II RECHERCHE 29 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

CHAPITRE 3 : PRESENTATION GENERALE DE LA METHODE ET DU
DISPOSITIF EXPERIMENTAL

3.1. INTRODUCTION

Le contrôle par ultrason est un procédé de contrôle non destructif semblable aux techniques RADAR ou SONAR. Il consiste à engendrer une impulsion ultrasonore dans le matériau et à observer les échos éventuels réfléchis par les discontinuités rencontrées. Les premières méthodes de contrôle étaient fondées sur la transmission d'ondes ultrasonores continues à travers des pièces contrôlées de formes simples (tôle, etc). la présence d'un défaut (manque des matières, discontinuité acoustique, etc) provoquait une dimunition ou une disparition de l'énergie ultrasonore transmise, mais il n'était pas possible de localiser en profondeur l'anomalie. L'évolution du matériel, avec en particulier l'utilisation d'impulsion brèves, a permis de faire évoluer le contrôle par ultrasons vers la technique par réflexion (écho d'anomalie) qui permet de localiser les défauts en profondeur. La méthode de contrôle par écho d'anomalie est la plus appropriée. Il s'agit de rechercher les signaux d'échos réfléchis par les anomalies ou défauts rencontrés lors de l'exploration de la pièce contrôlée.

3.2. LE CONTRÔLE PAR REFLEXION SUR ECHO D'ANOMALIE

3.2.1. Définition de la méthode

L'opérateur déplace le traducteur sur la surface de la pièce à contrôler, selon un mode opératoire appelé plan de sondage, qui permet d'assurer l'exploration de tout ou partie de la pièce à contrôler.

Pendant cette exploration, on peut distinguer deux phases essentielles : détection et caractérisation

3.2.1.1. La détection

Lors de l'explôration, l'opérateur doit surveiller l'apparition d'échos dont la position et l'amplitude sont révélatrice d'une anomalie.

· La position

La position de l'écho permet de localiser le réflecteur. A cette fin, il est nécessaire de faire précéder le contrôle d'un étallonage de la base des temps. Il s'agit de régler l'échelle horizontale pour garantir la parfaite correspondance entre la position de l'écho sur l'écran et la position du réflecteur dans la pièce contrôlée.

MEMOIRE DE MASTER II RECHERCHE 30 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

· L'amplitude

L'amplitude de l'écho des anomalies permet d'estimer leur importance. Il n'a jamais été possible d'utiliser la mesure directe (en volt par exemple) en raison de la diversité des appareils utilisés. Il est, à cet égard fort difficile d'effectuer leur étallonage absolu. C'est pourquoi toutes les méthodes de contrôle par ultrasons sont actuellement fondées sur des mésures relatives à l'amplitude d'échos. On compare toujours l'amplitude d'un écho d'anomalie d'un réflecteur parfaitement défini.

Cette comparaison est définie comme la réflectivité de l'anomalie. Les différentes méthodes de mesures de la réflectivité utilisées sont les suivantes :

- écho de fond ;

- écho d'entaille ;

- courbe de correction amplitude distance (C.A.D.) ; - diagramme de reflectivité.

D'une façon générale, pendant le contrôle, il faut être attentif à l'apparition d'échos dont l'amplitude atteint le seuil dit de prise en compte. En effet, l'anomalie qui est l'origine de l'échos peut se revéler préjudiciable à la tenue mécanique de la pièce contrôlée (risque de rupture). Le seuil, qui dépend de la méthode de mésure choisie, est génélament définie dans les documents de contrôle.

3.2.1.2. La caractérisation

Lorsque le seuil de prise en compte est atteint, il est alors nécessaire de caractériser l'anomalie afin de permettre en aval de juger de l'acceptation ou du rebut. Les carctéristiques de base sont :

- Localisation,

- Mésure de l'amplitude de l'écho d'anomalie selon une méthode définie ci-dessus (appelée estimation de la réflectivité de l'anomalie).

3.2.2. Méthode de mésure de l'amplitude des échos d'anomalie (réflectivité)

3.2.2.1. Méthode d'écho de fond

Lorsqu'on contrôle une pièce qui possède deux faces parallèles (ou assimilable à deux faces parallèles), l'écho réfléchi par la face opposée est appélé écho de fond. Plusieurs échos de fond

MEMOIRE DE MASTER II RECHERCHE 31 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

peuvent être visualisés compte-tenu d'aller et retour successif de l'impulsion ultrasonore dans l'épaisseur de la pièce (voir fig. 3.1 annexe 4).

L'amplitude de l'écho d'anomalie est caractérisée par une grandeur K égale au rapport entre la hauteur de l'écho d'anomalie et la hauteur de l'écho de fond relevée dans une région saine de la pièce (au voisinage immédiat d'une anomalie).

3.2.2.2. Méthode de la courbe expérimentale C.A.D.

Pour remédier aux inconvénients de la méthode de l'échos de fond, il est d'usage d'établir une Correction Amplitude Distance (C.A.D.). Cette correction se traduit généralement par une courbe tracée sur l'écran de l'appareil de contrôle et reliant les amplitudes d'échos (relévé) de réflecteur de même type situé à des distances différentes (fig. 3.2 annexe 4).

L'allure et la pente de la courbe varient en fonction du traducteur utilisé et des déflecteurs choisis (dimensions, forme ). En pratique, l'amplitude de l'écho d'anomalie est définie par le rapport (exprimé en pourcentage) entre la hauteur de l'échos sur l'écran et la hauteur de la courbe C.A.D. pour la même profondeur.

Hauteur écho d'anomalie

A = 100

3.3. MISE EN OEUVRE DU CONTRÔLE ULTRASONORE

3.3.1. contrôle par contact - contrôle par immersion

Les ultrasons aux fréquences utiliséses ( 1 à 10 MHZ ),ne se propagent pas dans l'air.Pour assurer le passage des ultrasons entre le traducteur et la piece à contrôler, il faut placer entre les deux un milieu dit de couplage .Deux techniques existent pour assurer ce couplage : le contrôle par contact et le controle par immersion.

3.3.1.1. Contrôle par contact

Le traducteur est directement placé sur la piece à controler. La liaison acoustique est assurée par un film d'agent de couplage qui est généralement soit une graisse ou une huile,soit de la colle cellulosique,soit des gels spéciaux ( fig 3.3 annexe 4). L'épaisseur du film de couplage est de l'ordre du dixieme de millimetre.

MEMOIRE DE MASTER II RECHERCHE 2008-2009

32

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

3.4.1.2. Contrôle par immersion

La technique expérimentale, utilisée pour la mesure des vitesses de propagation des ondes ultrasonores de volume en incidence oblique, est une technique impulsionnelle en immersion. La première mise en oeuvre de cette méthode réalisée par Markham en 1970 a été, depuis, largement utilisée et améliorée par différentes équipes [10], [11], [12].

L'éprouvette, sous forme de lame à faces parallèles de surfaces régulières et d'épaisseur e est placée dans un liquide de couplage (dans notre cas de l'eau) entre un émetteur Å et un récepteur R dont les faces sont planes et parallèles. Cette configuration permet de faire varier l'angle d'incidence i de l'onde plane générée par l'émetteur E par rapport à la normale à la face de l'échantillon. 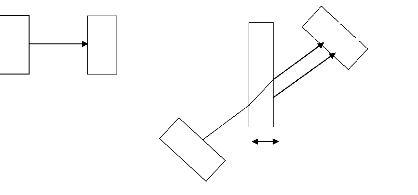Dans le cas le plus général, trois ondes de volume peuvent être générées au sein du matériau par conversion de mode à l'interface eau/matériau : une onde quasi longitudinale et deux ondes quasi transversales [5]. La figure 2.11 présente les différents parcours ultrasonores considérés par la suite.

R'

R

D

Signaux de mesure

C

i_r

E

R

Signal de référence

B

i_m

e

Fig. 3.1.Principe de la mesure de vitesses en incidence oblique

E

La mesure de vitesse commence par l'acquisition d'un signal dit de référence qui correspond au trajet (ER) d'une impulsion entre l'émetteur E et le récepteur R dans l'eau. Une fois l'éprouvette placée entre l'émetteur E et le récepteur R, le signal dit de mesure, correspondant au trajet (EBDR') d'une impulsion ultrasonore, est à son tour enregistré. La vitesse de propagation, correspondant au trajet (BD) dans l'éprouvette, est alors déduite de l'écart ô₁ = t m - t_r des temps de

propagation des signaux de mesure et de référence :

EB DR

+ ' BD ER BD BC

ô₁ = - =

t t

+ - = - (3.1)

m ^r V V V V V

eau eau eau

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

V et _Veau sont respectivement la vitesse recherchée au sein du matériau et la vitesse dans l'eau. A partir de considérations géométriques simples l'expression de ô devient :

e e r

cos( 1)

-

ô = - (3.2)

¹ r r

cos V _eau cos r

L'angle de réfraction r est déduit de la loi de Snell-Descartes à l'interface eau/échantillon :

(3.3)

V

r= arcsin - i

sin

V eau

La substitution de l'expression (3.3) dans l'équation (3.2) conduit après simplification à la vitesse de propagation V de l'onde ultrasonore dans le matériau :

eV eau

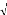
e 1 + 2 ô 1 cos

V e V i

eau eau

² + ô ²

V = (3.4)

Ainsi, la mesure de vitesse de propagation V d'une onde ultrasonore en incidence variable dans un matériau donné, fait intervenir la vitesse de propagation dans l'eau _(Veau). L'épaisseur e de l'éprouvette, l'angle d'incidence i du faisceau ultrasonore et la différence de temps de vol ô₁

obtenue, dans notre cas, par inter corrélation des signaux de mesure et de référence.

A partir de différents temps de vol et de la vitesse des ultrasons dans l'eau _Veau, il est possible de déterminer simultanément e et la vitesse longitudinale en incidence normale Vl [12]

Ce chapitre a permis de faire un tour d'horizon rapide des principes généraux de la méthode expérimentale, et de fournir les éléments éventuels concernant le contrôle de nos éprouvettes. La méthode retenue ici est la méthode de mesure de l'amplitude des échos d'anomalies(échos de fond) à l'aide d'une technique de contrôle ultrasonore dite contrôle par contact. Pour cela nous devrions, pour exécuter un contrôle de nos éprouvettes, se référer à une procédure particulière précise. Nous devons fixer dans le détail les méthodes choisies, les plans de sondage, les critères de prises en compte et la façon de caractériser les anomalies.

Le prochain chapitre nous permettra de présenter dans les détails la phase pratique de nos

essais

2008-2009

33

MEMOIRE DE MASTER II RECHERCHE

MEMOIRE DE MASTER II RECHERCHE 34 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

CHAPITRE 4 : REALISATION DES ESSAIS PRATIQUES
ULTRASONORES SUR UN MATERIAU COMPOSITE(ESSAI DE
DETECTION DES GONDOLEMENTS )

4.1. INTRODUCTION

Cette partie présente les informations pratiques éssentielles sur la façon dont les éssais ont été menés.Ces éssais se comportent en deux phases :

- exploration du volume de l'éprouvette controlée en vue de la détection des anomalies(gondolages) ;

- caracterisation des éventuelles anomalies décélées ( détermination des parmètres de détection ).

L'exploration est manuelle.Les principes de bases sont contenus dans les différentes opérations qu'il implique.Pour assurer la bonne transmission des ondes ultrasonores entre le traducteur et la pièce, de meme qu'un bon couplage acoustique ,un produit liquide de couplage a été nécessaire (ici la graisse ).

4.2. PRESENTATION DES EPROUVETTES ET DISPOSITIF D'ESSAI

4.2.1. Des éprouvettes

Nos éprouvettes sont des matériaux composites unidirectionnels fibre /platre, de dimensions 130 x 100 x 25 (mm ) (figure.4.1). Les fibres utilisées sont des fibres naturelles du "Rhectophyllum camerunense" de la region du Sud Cameroun. Ces fibres ont une couleur marron et d'une section circulaire avec un diamètre variant entre 0.20 et 0.70 mm. Le platre utilisé est un produit du gypse importé disponible dans le commerce.

Fig.4.0. Présentation des échantillons

MEMOIRE DE MASTER II RECHERCHE 35 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

4.2.2. Fabrication et mise en oeuvre des composites

Pour fabriquer notre composite, nous dévons préparer des moules. Il est nécessaire
d'enduire les surfaces d'un agent de démoulage.Nous emploierons ici une solution aqueuse de svon
de Marseille . Le savon est gras , celui-ci empechera l'adhérence du platre et il neutralisera aussi la
porosité des surfaces absorbante. Le savon de Marseille sera posé dans un récipient contenant de un
peu d'eau chaude car la detrempe du savon est assez rapide etproduit un gel blanchatre visqueux.
Prendre la solution visqueuse à l'aide d'un pinceau et enduire les surfaces devant recevoir le platre.

Le platre qui doit occuper environ un volume proche de 1.3 litres dans le coffrage, sera préparé dans les proportions de 1.5 Kg de platre pour 1 litre d'eau. La densité absolue du platre de Paris est d'environ 2.63. Gaché dans les proportions indiquées précédemment, onobtien donc un volume de 2075 litres de platre liquide ayant un poids de 4.38 Kg (1.75 Kg d'eau + 2.63 Kg de platre). Après battage avec un fouet de cuisine ,jusqu'à l'obtention d'un mélange homogène.On verse doucement le contenu dans les moules rectangulaires de 130x100x25 (mm) ou sont installées les fibres , puis on remue lentement par alternance avec la spatule pour faire remonter les bulles d'air en surface.

Nous avons fabriqué deux lots de type d'échantillons :

· Un lot de composite à base des fibres du R.C sans défauts artificiels.

· Un lot de composite à base de fibres avc défauts artificiels (Gondolements).

Le démoulage se fait 24 heures après la fabrication .Toutes les plaques sont conditionnés à l'air ambiant du laboratoire jusqu'à 10 jours.

4.2.3. Dispositif ^d'essaiL'appareillage comporte un ensemble électronique appelé « appareil ultrasonore » et un traducteur qui lui est relié electriquement( fig 3.5 annexe 4).

L'appareil ultrasonore comprend principalement :

· un émetteur : il fournit au traducteur l'énergie électrique nécessaire pour le mettre en vibration pendant un temps tres bref ;

· un récepteur :il recueille et met en forme le signal ;

· un écran de visualisation : il permet d'identifier les échos ultrasonores par leur amplitudes (verticale ) en fonction de leur instant d'apparition (horizontale )

MEMOIRE DE MASTER II RECHERCHE 36 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Le role du traducteur est d'émettre une impulsion ultrasonore dans le matériau et de recueillir les échos.

4.3.PREPARATION DU CONTROLE MANUEL

L'exécution du controle a été nécessairement réalisée en 4 étapes de préparation :

· vérification du bon fonctionnement de l'appareil ;

· règlage de la base de temps ;

· règlage de la sensibilité ;

· plan de sondage.

Au terme de cette 4eme étape, nous avons préparé également les documents nécessaires au dépouillement et à la rédaction du compte rendu.

4.3.1. Vérification de l'appareillage

Les opérations ici consistent à s'assurer visuellement du bon état des cables et des traducteurs (aucune dégradation ne doit apparaître ).nous avons vérifié les linéarités horizontales et verticales de l'écran ainsi que la justesse du réglage de gain ( atténuateur calibre ).

4.3.2. Etalonnage de la base de temps

L'étalonnage de la base de temps de l'apparail de contrôle par ultrasons a pour but d'établir une correspondance entre la position d'un écho,mesurée en nombre de carreaux,et le parcours ultrasonore. Nous avons donc fais deux réglages successifs pour étalonner la base de temps de cet appareil en prenant en compte les caractéristiques propres :

- aux matériaux ( vitesse de propagation ) et à l'échelle choisie ; - au traducteur et au couplage.

Le premier réglage ( échelle) nous a permi d'étalonner plus ou moins l'échelle horizontale pour aboutir à une échelle représentative en millimètre par carreau.

Le second réglage ( décalage ) nous a permi de compenser le temps de parcours préliminaire dans le transducteur afin que la position horizontale zéro corresponde à un parcours ultrasonore nul ( point d'entrée de l'onde dans le matériau ou point d'émergence en contrôle par contact ).

MEMOIRE DE MASTER II RECHERCHE 37 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

4.3.3. Réglage d'amplification

Il s'agit d'une étape essentielle dans la préparation des éssais.En effet ,une amplification insuffisante ne permet pas de détecter d'éventuels défauts.

A l'inverse, une amplification trop importante risque de noyer les informations dans un bruit (écho intempestif lié à la structure métallurgique de la pièce).

Pour s'assurer de la validité des mésures d'amplitude d'écho quelques vérifications rapides ont été réalisées.

En particulier il s'agit de :

· s'assurer de l'absence de seuil résiduel ;

· vérifier globalement le fonctionnement de l'atténuation calibrée ;

· vérifier rapidement la linéarité verticale.

4.4. EXECUTION DES ESSAIS

4.4.1. Le plan de sondage

Le plan de sondage est un mode opératoire qui définit les positions successives du traducteur
permettant d'explorer au mieux tout le volume de la zone à controler.Pour cela nous avons délimité
la surface de contrôle et préparé un référentiel de repérage des positions du traducteur.

4.1.chaine de mesure

MEMOIRE DE MASTER II RECHERCHE 38 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Le plan de sondage étant établi, il s'agit de passer aux éssais, c'est-à-dire de déplacer le traducteur sur la surface de l'éprouvette à controler.Il importe que l'opérateur s'éfforce de maintenir le couplage de façon constante.

En outre, il faut surveiller en permanence l'écran de l'appareil afin d'être informé de l'apparition d'échos d'anomalies. Nous faisons un recouvrement à 20 /100 du diamètre du transducteur,la distance entre 2 lignes successives de balayage est égale à 0,8 fois le diamètre du transducteur.

4.5. PRESENTATION DES RESULTATS DE L'ESSAI ET COMMENTAIRES

Les travaux se sont déroulés dans le laboratoire de contrôle par ultrasons de HYDRAC sis

au siège de Bassa à Douala.

Le contrôle par ultrasons étant en fait un contrôle de comparaison, pour détecter les éventuels défauts dans une pièce.

Le déroulement du contrôle est le suivant :

· Etalonnage de l'appareil en utilisant un bloc étalon en acier au carbone ;

· Etalonnage de l'appareil en utilisant un échantillon de composite sain (absence de défauts);

· Contrôle du matériau composite comportant des défauts artificiels et recueil des résultats. L'objectif est de rechercher et retrouver ces défauts artificiels matérialisés sous forme de gondolements (Sinuosités) ;

4.5.1. Etalonnage de l'appareil en utilisant un bloc étalon en acier au carbone Il s'agit d'une étape essentielle dans la préparation du contrôle.

Tableau.4.1 : Caractéristiques des appareillages utilisés

Item	Désignation	Nature	Marque	Type	Numéro de série	Fréquence	Dimension
1	Pièces de tests	Matériau composite Plâtre + fibre	-	-	-		130 x 100 x 25
		Acier au carbone	IIW (Institut international de soudure)	Bloc V2			Epaisseur 25mm
2	Appareil Ultrasons	Digital A-scan	SONATEST	Site scan 140	1401151C	15MHZ
3	Palpeur	Piézo- électrique	Krautkramer	BS4/Single	57746- 08169	Ø24 - 4MHZ
4	Couplant	Graisse	Eldon's	High quality	-	-	-

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

5

Câble coaxiale

-

Krautkramer

Gros/single

-

1m

Tableau.4.2 : Résultats de l'étalonnage sur un bloc étalon normalisé (acier au carbone)

Item	Désignation	Résultats
		Vitesse de l'onde longitudinale (m/s)	Zéro du palpeur			Echelle (mm)	Gain (dB)	Amplitude du 1^er écho par rapport à l'origine 0	Amplitude du 2^ème écho par rapport à l'origine 0
1	Bloc étalon, type A	5895	2.081			50	47.0	87%	66%
				1er écho à 25 mm de l'origine 0 (ou 1^er écho de fond) 2ème écho à 50 mm de l'origine (ou 2^ème écho de fond)
					écho initial à l'origine (écho de surface)

Echo initial à l'origine ou Écho de surface

MEMOIRE DE MASTER II RECHERCHE

39

2008-2009

Figure.4.2.Représentation A-scan des échos du bloc étalon

4.5.2. Étalonnage de l'appareil en utilisant un échantillon de composite sain

Le but de l'étalonnage est d'établir une correspondance entre la position d'un écho mesurée et le parcours ultrasonore

Tableau.4.3 : Résultats de l'étalonnage sur un échantillon de composite sain

Item	Désignation	Résultats
		Vitesse de l'onde (m/s)	Zéro du palpeu r	Echelle (mm)	Gain (dB)	Amplitude du 1er écho par rapport à l'origine	Amplitude du 2^ème écho par rapport à l'origine
2	Matériau composite	5895	2.081	50	47.0	0%	0%

MEMOIRE DE MASTER II RECHERCHE 40 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Figure.4.3. Représentation A-scan de l'écho de l'échantillon I

Commentaires :

On remarque l'absence d'écho de fond lorsqu'on passe de l'acier au composite. Ceci est dû à la forte atténuation du matériau composite (plâtre), les vitesses de propagation des ondes n'étant pas les mêmes dans ces matériaux. Il faudra donc trouver la vitesse des ondes dans le composite.

Tableau.4.4 : Résultats de l'étalonnage sur un échantilon de composite sain

Item	Désignation	Résultats
		Vitesse de l'onde (m/s)	Zéro du palpeur	Echelle (mm)	Gain (dB)	Amplitude du 1^er écho de fond par rapport à l'origine	Amplitude du 2ème écho de fond par rapport à l'origine
1	Acier au carbone	6631	3.004	0 - 50	85.5	Plus de 100%	Plus de 100%
2	Matériau composite	6631	3.004	0 - 50	85.5	76%	Le % n'est pas appréciable

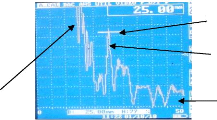
Amplitude du 2^ème écho de fond confondu avec le bruit de fond

Echo initial à l'origine ou écho de surface

Gate ou porte indiquant la position exacte de l'écho

1er écho à 25 mm de l'origine ou 1er écho de fond

Figure.4.4. Représentation A-scan des échos sur échantillon II

Commentaire :

L'étalonnage a été fait sur le matériau composite en utilisant une vitesse de propagation obtenue par approximation, ceci a permis d'obtenir au moins un premier écho de fond dont l'amplitude est à 76% de la hauteur de l'écran.

Le second n'est pas clairement visible car confondu avec le bruit de fond. Ceci peut s'expliquer par la composition du matériau qui comporte une structure à gros grain. Cette structure non seulement attenue les ondes mais aussi les disperse. On remarque également que si on applique

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

la même vitesse à l'acier au carbone, on obtient des échos dont l'amplitude dépasse largement la hauteur de l'écran.

Tableau.4.5 : Résultats de l'étalonnage sur un échantillon de composite sain

Désignation	Nature	Marque	Type	Numéro de série	Fréquence
Palpeur	Piézo- électrique	Krautkramer	Single	73433	Ø12-2MHZ

On reprend les mêmes paramètres, mais on change de palpeur et la vitesse est légèrement modifiée.

Tableau.4.6 : Résultat de l'étalonnage

Item	Désignation	Résultats
		Vitesse de l'onde (m/s)	Zéro du palpeur	Echelle (mm)	Gain (dB)	Amplitude du 1er écho par rapport à l'origine 0	Amplitude du 2^ème écho par rapport à l'origine 0
1	Acier au carbone	6217	1.583	0 - 50	62.6	Plus de 100%	Plus de 100%
2	Matériau composite (plâtre + fibre)	6217	1.583	0 - 50	62.6	72%	12%

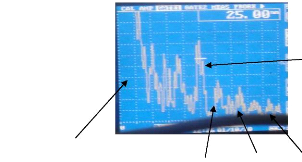
Echo initial à l'origine 0

1er écho de fond à 25 mm de
l'origine 0

MEMOIRE DE MASTER II RECHERCHE 41 2008-2009

Echos de fond dû à la nature du matériau

Figure 4.5 : Représentation A-scan des échos III

Commentaires :

On constate qu'en utilisant un palpeur de fréquence faible, on obtient au moins le 2^ème écho de fond. C'est avec ces paramètres que les contrôles des échantillons comportant des défauts

Commentaires :

MEMOIRE DE MASTER II RECHERCHE 42 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

artificiels ont été conduits. Cette expérience a été répétée avec d'autres palpeurs de faible fréquence et le résultat a été le même.

4.5.3. Contrôle du matériau composite comportant des défauts artificiels (gondolements)

La caractérisation d'une anomalie implique la détermination des différents paramètres parmi lesquels la réflectivité (amplitude de l'écho) est primordiale.

Tableau.4.7 : Résultats du Contrôle de notre matériau composite avec défauts

Désignatio n

Nature

Marque

Type

Numéro de série

Fréquence

Palpeur

Piézo- électrique

Krautkrame r

Single

73433

Ø12-2MHZ

Item

Désignation

Résultats

Vitesse de l'onde (m/s)

Zéro du palpeur

Echell e (mm)

Gain (dB)

Amplitude du 1er écho par rapport à l'origine 0

Amplitude du 2^ème écho par rapport à l'origine 0

1

Matériau composite (plâtre + fibre)

6217

1.583

0 - 50

62.6

37%

20%

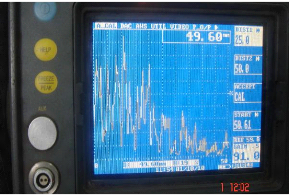
Fig.4.6. Représentation A. scan des échos IV

MEMOIRE DE MASTER II RECHERCHE 43 2008-2009

CONTRIBUTION Á LA DÉTERMINATION DES PARAMÈTRES ULTRASONORES DES GONDOLEMENTS DES FIBRES DANS UN MATÉRIAU
COMPOSITE Á MATRICE CERAMIQUE RENFORCÉ DES FIBRES DU «RHECTOPHYLLUM CAMERUNENSE».

Les échos obtenus nous ont permit de constater la nature hétérogène de notre matériau composite. Nous observons que le second écho de fond a pu être obtenu.