Simulation numérique d'une flamme turbulente prémélangée axysimétrique par le code fluent

CHAPITRE I

AEROTHERMOCHIMIE ET STOECHIOMETRIE

1) Introduction

Un gaz en réaction est un mélange non isotherme d'espèces multiples (hydrocarbures, oxygène, eau, dioxyde de carbone, etc.) qui doivent être suivies individuellement et instantanément. Les données thermodynamiques sont également plus complexes que dans l'aérodynamique classique car les chaleurs spécifiques changement dans le gaz réactif de façon significative avec la température et la composition.

v' Les espèces réagissent chimiquement avec des vitesses (taux de réactions) qui exigent des modélisations spécifiques.

v' Etant donné que le gaz en réaction est un mélange de plusieurs espèces, les coefficients de transport (diffusivité thermique, diffusion des espèces, viscosité, etc.) nécessitent une attention particulière.

La dérivation des équations de conservation de la masse, des espèces ou des bilans d'énergie peut être trouvé dans les ouvrages classiques tels que ceux de Williams, Kuo ou

M ?

Candel [6]. Dans ce chapitre on se limite à citer les différentes formes utilisées dans les

M ?

codes de calcul et sur leurs implications pour des techniques numériques 2) Choix des variables primitives

La combustion implique multiples espèces qui réagissant dans diverses réactions chimiques. Ces espèces sont caractérisées par leurs fractions massiques Yk pour k = 1 à N, où N est le nombre d'espèces dans le mélange réactif. Les fractions de masse Yk sont définis par:

(1.1)

Où Mk et sont respectivement : la masse et la densité de l'esSqFeINIprésente dans un

volume donné V, M est la masse totale de gaz dans ce volume.

Les variables primitives pour le cas tridimensionnel réactif sont:

·

(1.4)
(1.5)

(1.6)

La densité,

(1.2)

· Les vitesses dans les trois directions _i (i=1,2 et 3)

· Une seule variable pour l'énergie (enthalpie h ou température T)

· Les fractions massiques Yk des espèces

Il faut donc calculer N+5 variables au lieu de 5 dans le cas non réactif. Sachant que la combustion implique un grand nombre d'espèces (N est supérieur à 50 pour la plupart des hydrocarbures simples), l'effort de calcul est considérable dans la simulation des

n M

k

X Y

écoulements réactifs (vu le nombre d'équations de conservation à résoudre). n M

tot k

3) Notions sur la thermochimie

Il est nécessaire de définir quelques variables usuelles ainsi que des notions de la thermochimie. Commençons par l'équations d'état du gaz parfait qui relie la pression, la température et la densité du gaz en question:

(1.3)

Pour un mélange gazeux la masse molaire du gaz est calculée par :

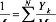
La fraction molaire Xk de l'espèce k s'écrit :

Où n est le nombre de molles.

La concentration [Xk] de l'espèce k est donnée par :

T

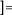
L'énergie sensible de l'espèce k est donnée par :

(1.7)

I.'entIia1pie sensible J.e III 1 I 11111 II I I 1111111111 II

33 33 3

IE1.' LI Ll1IpLIL1I Lillilil I I I I I III I I III I I I I HI I I I I I I I I I I I I liii I I I I I II I I II I 1IflJ JJ LII I III I I I Ii

IIIIIIIIIII!

33 3' 3

LIILLI] ' LLIientha1pie JLflhi1JI III HII 11111 IL II H

33 33 ' 3

I H IL Ij LiIIIJJLIJ_p H I I I H I H I H I ILl H H II I H HIll I liii H I I1IJI I I I I I H ₁₁₁₁₁ LH I H Hi _I' LI Hill IWH'erithalpie

LLImJI1Lour former 1kg de l'i I I III ILIIIIIII III H ILLhIL1J p I IIJJ' II

33 33 3 3

____ 1 i iii ii	^3LJJ L1		Ahm fk ^3LJ fflLJ^3L1
		''''JLI1
		'J'''LI1	'^3''^33L11
		!33J!	'J' JLI1
			''''JLI1
		'^3'''JLI1	'J'^333LI1
	3! !	!	!
	3! !	!	!
	'^3'J^3LI1	'LII	'LII

4) La stoechiométrie dans les flammes prémélangées

Dans la combustion prémélangée le fuel et l'oxydant sont mélangé avant d'entrer dans la chambre de combustion.

Considérons la réaction globale suivante

Par exemple ( + o0. --> CO. + oll.0 ). Les constantes sont les coefficients

stoechiométriques correspondants au fuel et à l'oxydant.

m n défini le rapport stoechiométrique s par

(1.12

(1.13

(1.1

La richesse du mélange est définie p

Qui s'écrit aussi

vec et sont les débits massiques du fuel et de l'oxydant

La richesse est un paramètre principal pour les gaz prémélangé

· 0 > 1 combustion riche en fuel

· 0 < 1 combustion pauvre en fuel

Dans les flammes hydrocarbures/air, CIEIBFtiR(EP DAiqXe EdXEIXeEEstATFKiRP pITiIXeE ( =1 ) est donnée par :

(1.15)

/ IiIEpta(tEFRP SRspEd'X(eEP RleEE'Rx\ Jq(eETIET.76 EP ROEdIE(itARTq(1E3(EYRlXP Hi ELe tableau suivant donne quelques valeurs du coefficient VATFKiRP pITiqXeEsEItElEEIrIFtiR(E P DAiqXIEstATFKiRP ptriqXe EdXEIXel ( =1).

Réactions globale	s	Y:
CH4 +2(02 +3.76N2) -*CO2 +2H20 +7.52N2	4.00	0.055
C3H8 +5(02 + 3.76N2) -->3CO2 +4H20 +18.8N2	3.63	0.060
2C81/18 + 25(02 + 3.76N2) -->16CO2 +18H20 + 94N2	3.51	0.062
2H2 + (02 + 3.76N2) --> 2H20 + 3.76N2	8.00	0.028

Tableau (1.2) :valeurs de S et Y pour quelque réactions

&I EtIRDIXEP R(t11E1Xe ESRXrEaYRi1EX(e EFRP FXstiR(EstATFKiRP pITiqXE, ENEqXE(titpEdXE combustible injectée est très faible comparativement à l'air qui est composé en grande partie par l'azote.

5) Equation de conservation des espèces

Puisque notre travail consiste à étudier les écoulements réactifs, on va détailler la procédure de déduction de l'équation de conservation de la masse de n'importe quelle espèce dans un mélange multi composants. Cette déduction va se faire en prenant simultanément le taux de réaction en g 3 et en 3 ce qui va permettre d'introduire le loi de Fick.

Nous commençons par faire un bilan de masse sur un élément fluide arbitraire dans un mélange binaire. Appliquons la loi de conservation de la masse sur un élément de volume

z fixe dans un espace à travers lequel un mélange binaire des espèces A et B s'écoule et réagit.

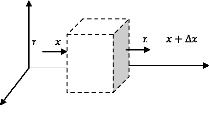
y

? I

? I

X

Figure(1.1)

Z

Dans ce volume de contrôle infinitésimal, l'espèce A peut être produite ou consommée par réaction chimique avec un taux ? g 3 . Si ? , l'espèce A est consommée. Les différents thermes qui contribuent à l'équilibre massique sont :

Le taux d'accumulation de la masse de l'espèce dans le volume de contrôle

t z (1.16)

Les flux de A entrants et sortants dans le volume par la direction x respectivement aux positions x et sont

?

/ z (1.17)

Et	?	?
/ z			/ z

?

z (1.18)

Le taux de production de l'espèce A par la réaction chimique ? z

?

est le taux de production spécifique de A.

Le même principe est appliqué aux autres directions, on somme puis on divise par z ce qui donne :

( ?

?

? ~

~ ) ? (1.19)

~

C'est l'équation de continuité du composant A, elle					aussi appelée l'équation de
?			?				?
conservation du masse d'espece A. Les quantités								^z sont les composantes
						z

scalaires du vecteur du flux de masse ? , dans le rectangle de coordonné. Dans la notation

vectorielle, l'équation s'écrit :

t rh ci) (1.20)

D e la même façon, l'équation de la continuité du composant B est

t B rh ci) (1.21)

D ans un mélange binaire, une espèce peut se convertir vers l'autre et vice versa. Le taux

de production d'une espèce et égal au taux de destruction de la deuxième ce qui implique

que la somme des équations (1.20) et (1.21) donne l'équation de conservation du mélange

t V (1.22)

Pour obtenir l'équation (1.22), on a utilisé ? ? l et ? ?

Pour un fluide de densité massique constante l'équation (1.22) devient : ~

G On va maintenant faire le développement en terme de 3 , Si ? est le

taux molaire de production de A par unité de volume, alors l'analogue molaire de l'équation (1.20) est :

c t

?

?

(1.23)

En remplaçant ? V -- ~ dans l'équation (1.20) on obtient :

t V Y ? (1.24)

Avec l la vitesse massique de diffusion et dans B

En remplaçant aussi ? V -- dans l'équation (1.24) on obtient :

C t

V

?

(1.25)

Oil V est la vitesse molaire de diffusion [6]

Si on a pas de réaction chimique, les taux de réactions massiques et molaires ? , ? , ? , et ? sont nuls. Si en plus, V est nulle dans l'équation 5 ou ~ est nulle dans l'équation

6, on obtient :

c t

(1.26)

Cette relation est dite "la deuxième loi de Fick de diffusion" . Cette équation est généralement utilisée pour la diffusion dans les solides, les liquides stationnaires,... Cette équation est similaire à l'équation de la conduction de la chaleur :

(1.27)

t

A l'aide de les relations ~ et v v V pour un système multi composants,

l'équation 3 devient :

~ [~ ~ V ] ? (1.28)

t

L'équation ci-dessus dans sa forme de divergence peut être réduite à la forme d'Euler. Par expansion des termes à gauche on a :

Y

t

Y

t

~ ~ ~ ~ ~ ~ ? (1.29)

Alor on obtient :

t

Y v( ? Y ) -- v( ) ? (1.30)

Avec le flux de diffusion moléculaire. On adopte la loi de Fick pour le transport diffusif de la masse :

?

_ Y (1.31)

Avec le coefficient de diffusion moléculaire de l'espéce .

6) Mécanismes réactionnels et taux de réaction

On a vu que chaque espèce dans le mélange gazeux doit être représentée par une équation de conservation. Cette dernière décrit l'évolution de l'espèce donnée dans l'espace et dans le temps. Dans le milieu réactif, plusieurs espèces entrent en compétition chacune avec un taux de réaction bien déterminé.

Pour expliquer la méthode de calcul du taux de réaction, prenons une partie d'un mécanisme réactionnel de la combustion de l'hydrogène dans l'oxygène -- .

(1.33) (1.34) (1.35) (1.36) (1.37) (1.38)

Ou Kf et K sont les coefficients du taux élémentaire de réaction dans le sens direct (gauche à droite) et dans le sens inverse de la réaction j.

Par exemple, le taux net de production d'oxyg~ne est la somme de tous les taux élémentaires des réactions qui produisent l'oxyg~ne moins la somme de tous les taux élémentaires des réactions qui consomment l'oxygqne.

[0 1 t

~ [ ][ ] K [ ][ ] K [ ][ ]

--Kf [ ][ ] -- Kf [ ][ ] -- Kf [ ] (1.39)

De la même façon, on peut écrire cette expression pour chaque espèce qui participe dans le mécanisme. Cela donne un ensemble d'équations différentielles ordinaires du premier ordre qui représentent l'évolution du système chimique à partir des conditions initiales :

[ ] t t

{[ ] [ ] ... [ ] } (1.40)

Avec [ ] [ ~

Une fois qu'on a trouvé taux de réactions élémentaires, on peut résoudre les équations de conservations des espèces et finalement trouver toutes les variables primitives.

7) Formulation générale pour le calcul du taux de réaction

Un mécanisme réactionnel peut être écrit sous une forme compacte, pour une réaction élémentaire i, qui combine N (j=1,N) espèces chimiques, on écrit

~ ~ì

? ~ ~ ~ìì

~ (1.41)

~

Où ~ì et ~ìì produits.

sont les coefficients stoechiométriques respectivement des réactifs et des

Pour expliquer cette notation, reprenons les réactions (1.33)- (1.38), qui combinent six espèces à savoir :

On définit j comme espèce et i comme réaction selon la table suivante:

j	Espèces	i	Réaction
1		1	(1.33)
2		2	(1.34)
3		3	(1.35)
4		4	(1.36)
5		5	(1.37)
6		6	(1.38)

D'autre part, on utilise j comme l'indexe des colonnes et i des lignes, ce qui donne une matrice des coefficients stoechiométriques

et

On remarque que la réaction élémentaire implique au maximum trois à quatre espèces réactives, ce qui fait que la matrice des coefficients est presque nulle lorsque le nombre d'espèce est grand.

Le taux de production de l'espèce j est calculé en sommant sur toutes les réactions i, il est donné par

cb E^l1₌ t q j=1.2...N (1.42)

0

Oil

^0Et

^iì ~ìì ?? ^1

-- ~ì (1.43)

q Kf ?ⁱ1= [ ] ì j -- K ?ⁱ1= [ ] ììi

(1.44)

Le taux de production ? correspond au terme gauche des équations (1.39) et (1.40), on a pour un mécanisme complet

?

[dt l (1.45)

L'équation (1.44) définit le taux de progression q pour la réaction élémentaire, par
exemple pour la réaction (1.33), on pose i=1ce qui donne

q Kf [ ] [ ] [ ] [ ~ [ ] [ ~

--K [ ] [ ] [ ] [ ] [ ] [ ] (1.46)

q Kf [ ] [ ] K [ ] [ ] (1.47)

De même façon on écrit les expressions pour i=2.3...6, et on somme l'équation (1.42) pour obtenir le taux de réaction ? .

Le calcul des constantes et constitue un problème central dans la modélisation

de combustion. Souvent, elles sont modélisées en par la loi empirique d'Arrhenius qui est basée sur l'observation expérimentale.

8) Approximation de la combustion par une seule réaction globale

Pour simplifier les calculs, on approxime la combustion par une réaction globale d'une mole de fuel avec « á » moles d'oxygène pour produire « â » moles d'un produit de combustion P

F á â 1 (1.48)

D'une part on facilite les calculs, et d'autre part perd des informations sur les espèces intermédiaires qui sont parfois très importantes.

'apr~s l'expérience, le taux de réaction du fuel est donné par

[ ] t

KG [ ] [ O ] (1.49)

Avec [ ] concentration molaire 3 de l'esp~ce i dans le mélange,

KG est le coefficient du taux global de réaction qui est généralement fonction de la température,

Les exposants n, m sont reliés aux coefficients stoechiométriques de la réaction, d'après l'équation (1.49) le fuel est dit d'ordre n et le combustible d'ordre m.

9) Approximation par un mécanisme réactionnel formé par des réactions élémentaires Dans le cas général, la combustion est approximé par un mécanisme réactionnel formé

par plusieurs réactions élémentaires. La plus part des réactions élémentaires concernant la combustion sont « bi moléculaires » c'est-à-dire deux molécules réagissent pour donner deux molécules différents :

Le taux de réaction s'écrit en fonction de la concentration molaire de [A]

[ ] t

3 K ano [ ] [ ] ( ) k o / (1.50)

Le coefficient K o est donné par [6]

(1.51)

*~ +

T

K o

Cette formule est donnée par l'expérience. Les constantes A, c et (l'énergie

d'activation) sont tabulées et donnée pour chaque mécanisme réactionnel.

Dans ce qui suit un exemple qui montre un mécanisme réactionnel _H2-O2 (9 espèces et 19 réactions) écrit sous un format universel dit format : CHEMKIN [8] (les commentaires entre parenthèses ne font pas partie du mécanisme, elles sont données à titre explicatif)

ELEMENTS

H O N F (dans cette ligne on un les elements chimiques)

END SPECIES

H2 O2 OH O H H2O HO2 H2O2 N2 F (ici les espèces chimiques)

END

REACTIONS F ( dans ce qui suit les reactions élémentaires)

(Réaction const. A c Ea)

H2+O2=OH+OH 1.700E13 0.0 47780.0

H2+OH=H2O+H 1.170E09 1.30 3626.0

H+O2=OH+O 5.130E16 -0.816 16507.0

O+H2=OH+H 1.800E10 1.0 8826.0

H+O2+M=HO2+M 2.100E18 -1.0 0.0
H2/3.3/ O2/0./ N2/0./ H2O/21.0/

H+O2+O2=HO2+O2 6.700E19 -1.42 0.0

H+O2+N2=HO2+N2 6.700E19 -1.42 0.0

OH+HO2=H2O+O2 5.000E13 0.0 1000.0

H+HO2=OH+OH 2.500E14 0.0 1900.0

O+HO2=O2+OH 4.800E13 0.0 1000.0

Aérothermochimie et stoechiométrie			19
OH+OH=O+H2O	6.000E08	1.3	0.0
H2+M=H+H+M	2.230E12	0.5	92600.0
H2/3./ H/2./ H2O/6.0/
O2+M=O+O+M	1.850E11	0.5	95560.0
H+OH+M=H2O+M	7.500E23	-2.6	0.0
H2O/20.0/
HO2+H=H2+O2	2.500E13	0.0	700.0
HO2+HO2=H2O2+O2	2.000E12	0.0	0.0
H2O2+M=OH+OH+M	1.300E17	0.0	45500.0
H2O2+H=H2+HO2	1.600E12	0.0	3800.0
H2O2+OH=H2O+HO2	1.000E13	0.0	1800.0
END
10) Conclusion

Ce chapitre représente la formulation mathématique du phénomène, les détails de calcul du taux de production pour une réaction globale, la conservation des espèces. Ainsi, que des notions sur la thermochimie et la \toeFKLRP ptrLe.J