CHAPITRE II
NOTIONS SUR LA TURBULENCE
1) Introduction
Chacun est capable de citer des effets bien visibles de la
turbulence dans plusieurs cas dans la nature, elle est très proche de
nous, par exemple la fumée d'une cheminée ou le
développement d'un filet d'eau coulant d'un robinet.
Dans ces cas et d'autres, des structures tourbillonnaires
plus ou moins organisées rendent l'écoulement complexe et il
devient difficile d'en appréhender les détails, d'en
prédire précisément l'évolution instantanée
et locale, méme en mettant en oeuvre les moyens de calcul qui ne cessent
de voir leur puissance s'accroitre.
La prise en compte, plus ou moins raffinée, de
l'influence de ces structures est cependant indispensable dans une grande
partie des applications industrielle courantes.
2) Oü observe t on la turbulence?
La turbulence est un phénomène présent de
manière très facilement visible dans la nature :
v' Dans l'air : les rafales de vent, les mini-tornades dans le
désert, le panache de fumée des grandes cheminées,
turbulence atmosphérique : (tourbillons de taille > 1000 km).
v' Dans l'eau : le lait dans le café, les remous dans les
rivières.
v' Dans la mer : le Gulf Stream
v' Dans la terre : le mouvement des plaques continentales
v' Dans l'espace : l'atmosphère externe de Jupiter
Il est également très présent dans les
écoulements industriels :
v' Aérodynamique externe des voitures, des camions,
v' Sillage des avions
v' Aérodynamique interne dans les moteurs (combustion,
etc....)
3) Les deux points de vue sur la turbulence
Et pourtant, certaines grandeurs macroscopiques sont bien
reproductibles. Par exemple :
ü Traînée et portance d'une voiture dans une
soufflerie donnée
ü Débit d'une conduite á haut Reynolds
ü Puissance d'un moteur á combustion
ü Température maximale des disques de frein
ü Durée de persistance du sillage d'un avion de
ligne
ü Portance et traînée d'un avion
Les scientifiques ont alors deux points de vue possibles :
ü Soit chercher á moyenner directement la
turbulence, á lisser le phénomène : c'est le point de vue
statistique. On cherche uniquement les grandeurs moyennes, et l'énergie
cinétique turbulente moyenne. C'est une vision "figée" ou
"rationnelle" de la turbulence, souvent celle des numériciens.
ü Soit chercher á extraire la cohérence
dans la turbulence : c'est le point de vue des "structures cohérentes".
On cherche alors l'évolution des structures qui persistent au milieu du
chaos, celles qui vont déterminer la physique de l'écoulement.
C'est une vision instationnaire, fluctuante et plus expérimentaliste de
la turbulence.
4) LiHxSpUHQcHRSH 5 HyQIIdN EILEE3)
Cette expérience montre le phénomène de
la turbulence dans un écoulement turbulent, le colorant est rapidement
dispersé avec formation des structures sous forme de volutes,
appelées tourbillons. Dans cette situation, une mesure de la composante
axiale de la vitesse (par vélocimétrie, laser ou par fil chaud)
montre que celle-ci fluctue de façon aléatoire dans l'espace et
le temps [9].
La figure suivant montre les déférents
étapes de passage d'un écoulement laminaire à un
écoulement turbulent en passant par le profile de transitionnel
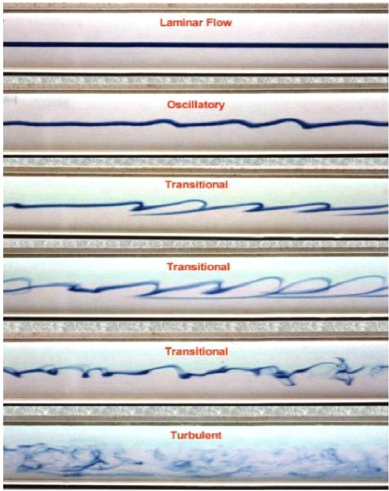
Figure (2.1) :Le passage d'écoulement laminaire vers
turbulent
5) Caractéristiques d'un écoulement
turbulent
En général, un écoulement turbulent peut
être caractérisé par les propriétés
suivantes: v' L'écoulement est instationnaire.
v' Incertitude (de mesure, de calcul).
v' Le vecteur de vitesse en un point varie de façon
aléatoire en direction et en module. v' L'écoulement contient un
grand nombre de tourbillons de taille très variée.
v' Augmentation du mélange : forte diffusion des
quantités transportées (exemple le lait et le café, la
fumée, etc.).
v' Le bruit : les écoulements turbulents sont bruyants
du fait des sources acoustiques créées par les fluctuations de
pression dans le fluide. Cela peut générer de l'inconfort dans
certains cas (exemple le bruit des rétroviseurs extérieurs des
véhicules),
v' Les effets de la turbulence sont parfois positifs, parfois
négatifs :
v' Effets positifs : l'augmentation du mélange permet
d'améliorer la combustion par exemple, d'améliorer la portance
des avions, de réduire la température. v' Effets négatifs
: diffusion de la pollution.
6) La transition du laminaire au turbulent
Le nombre de Reynolds a été introduit par Osborne
Reynolds en 1883. Il compare les termes de convection (non linéaires)
aux termes de dissipation visqueuse [10].
(2.1)
Au fur et à mesure que le nombre de Reynolds augmente,
on observe un changement de topologie de l'écoulement qui correspond
à la transition laminaire/ turbulent. Le nombre de Reynolds critique
correspond à ce passage, il est en général de l'ordre de
1000. Il prend
des valeurs différentes selon le type
d'écoulement. Quand Re << 1 les termes non linéaires (la
convection) sont masqués par la diffusion visqueuse, les
équations se rapprochent donc d'équations linéaires.
Quand Re >> 1, les termes non linéaires deviennent
prépondérants, et l'approximation linéaire n'est plus
possible.
· Pour un écoulement de Poiseuille
(écoulement dans un tube 1841), au delà de Re = 2000,
les quantités ne dépendent plus du nombre de Reynolds. Le
frottement est
proportionnel à ( ) au lieu de ( ) dans le cas
laminaire
ü Pour un écoulement de Couette (écoulement
entre deux plans infinis) :
ü Pour une couche limite sur plaque plane, on utilise le
nombre de Reynolds basé sur l'épaisseur de couche limite
ä
(2.2)
Pour Res = 5 20, la couche limite se développe suivant
un profil de Blasius en 8=- .
Pour 5 20 < Res < 2000 on a une zone de transition dans
laquelle se développent des ondes dites de Tollmien-Schlichting. Au
delà, des petites échelles apparaissent et on parle alors de
couche limite pleinement développée. Le nombre de Reynolds
correspondant basé sur la distance x depuis le démarrage de la
couche limite est d enviro n Rex = 106. Dans un
écoulement d'air à (10m/s) la couche limite devient pleinement
turbulente à environ (1m) du bord d'attaque.
ü Pour une couche de mélange (écoulement
qui résulte du mélange de deux fluides injectés à
deux vitesses différentes), le nombre de Reynolds critique basé
sur la vitesse moyenne; (U2 -- U1)/2 et sur l'épaisseur de couche de
mélange 8(x) et Rec = 25 00 environ
7) La cascade de KOLMOGOROV
La notion de Richardson (1881-1953) de la turbulence
était qu'un écoulement turbulent est composé de
tourbillons de différentes tailles. Les grands tourbillons sont
instables et meurent en se cassant en tourbillons plus petits, et
l'énergie cinétique du grand tourbillon initial est
divisée par les plus petits tourbillons qu`il a
généré. Ces petits tourbillons subissent le même
processus, provoquant encore de plus petits tourbillons qui héritent de
l'énergie de leurs tourbillons prédécesseurs, et ainsi de
suite [10]. De cette façon, l'énergie passe des grandes
échelles du mouvement aux plus petites échelles jusqu'à
atteindre une échelle suffisamment petite de longueur tels que la
viscosité du fluide peut efficacement absorber l'énergie
cinétique dans l'énergie interne, cette vision de cascade n'est
valable que d'un point de vu statistique.
Effectivement, la notion dynamique de cascade étape par
étape est dénuée de sens. Il existe une théorie qui
a contribué de façon majeure dans la compréhension de la
turbulence, la théorie de Kolmogorov (1941). Elle repose sur une vision
"statistique" de la turbulence, elle
dit que les tourbillons dans l'écoulement ont une
taille comprise entre les deux tailles limites suivantes [10] :
v' La plus grande échelle de l'écoulement L
(imposée par la géométrie de l'écoulement, par
exemple typiquement le diamètre d'un cylindre, le diamètre d'une
cheminée, ou encore la hauteur d'une voiture).
v' La plus petite échelle de l'écoulement :
imposée par la viscosité du fluide cette
échelle est appelée échelle de Kolmogorov,
ou échelle de dissipation visqueuse. L'ordre de grandeur entre et est le
suivant [25] :
4 (2.3)
La théorie de la "cascade" énergétique
prédit que les tourbillons ne reçoivent de l'énergie que
des échelles les plus grandes qu'eux, et la transmettent ensuite aux
échelles les plus petites qu'eux, et ainsi de suite jusqu'à la
plus petite échelle présente dans l'écoulement
`'l'échelle (ç)`'
On parle de production d'énergie lorsque les grosses
structures sont générées, par un décollement par
exemple, et de dissipation d'énergie lorsque les tourbillons
disparaissent complètement en aval de l'obstacle. Lorsque la production
d'énergie est égale à la dissipation d'énergie, on
parle de turbulence "en équilibre".
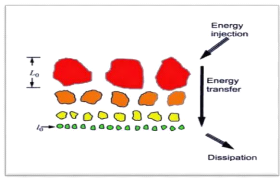
Figure (2.2) : Dessin schématique de la cascade de
KOLMOGOROV
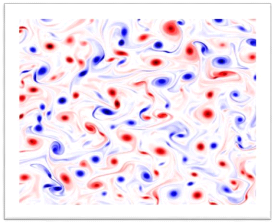
Figure(2.3) :Cascade de Richardson
8) Quelques types de simulation numériques de la
turbulence
Le besoin de recourir aux simulations numériques en
Mécanique des Fluides est aujourd'hui omniprésent dans de
multiples domaines d'applications (automobile, aéronautique et thermique
par exemple) et ce pour plusieurs raisons. Tout d'abord, les simulations
numériques permettent de comprendre les phénomènes
impliqués dans un écoulement : l'accès à certaines
informations est rendu possible, l'écoulement peut être
calculé et donc visualisé en 3D.
De plus, les simulations numériques permettent de
tester- l'influence de plusieurs paramètres sans avoir à
reconstruire tout un banc expérimental. On conçoit
évidemment qu'il est plus aisé, par exemple, de modifier un
maillage de turbine à gaz plutôt que de faire construire de
nouvelles pièces. Les simulations numériques peuvent
également permettre d'observer les comportements d'un écoulement
dans une géométrie à plus grande échelle ("scaling
up") sans pour autant nécessiter la construction de pilotes encombrants
(par exemple en lit fluidisé).
Il existe trois types de simulation numérique en
Mécanique des fluides : DNS (Direct Numerical Simulation), LES (Large
Eddy Simulation) et RANS (Reynolds Average Navier Stokes). Dans ces
dernières années, on note le développement d'une nouvelle
approche dite DES (Direct Eddy Simulation) qu'on ne va pas citer dans ce qui
suit.
8.1) La simulation numérique directe
(DNS)
Dans les simulations DNS, les équations de
Navier-Stokes sont entièrement résolues : la turbulence est
calculée et non plus modélisée. Ces simulations sont donc
des plus précises mais ont un coût de calcul beaucoup trop
élevé pour qu'il soit envisageable (du moins à ce jour) de
simuler une configuration industrielle en DNS. En effet, le nombre de points
nécessaire pour réaliser une DNS est directement lié au
nombre de Reynolds de l'écoulement
( 4 )[10]. Les simulations de type DNS sont donc limitées
à des calculs "académiques"
de type boîte cubique de petit côté, ou
bien à des écoulements à faible nombre de Reynolds.
Méme s'il n'est pas exclu qu'un jour les moyens de calcul autoriseront
de telles simulations. 8.2) La simulation des grandes échelles
(LES)
Les simulations LES résolvent les équations de
Navier-Stokes filtrées spatialement, seules les petites structures sont
modélisées alors que toutes les autres sont calculées. En
pratique, le filtrage spatial est imposé par le maillage : seules les
structures plus grosses que le maillage seront résolues.
Par ailleurs, des modèles, dits modèles de
sous-maille, sont introduits pour simuler la turbulence des petites
échelles. Avec ce genre de simulation, il est possible d'obtenir des
grandeurs moyennes mais également des grandeurs fluctuantes, ce qui fait
l'intérêt de la LES en comparaison aux simulations RANS. Les
coûts de calcul, certes plus importants que pour des simulations RANS,
restent raisonnables et autorisent la simulation de géométries
complexes sur des maillages raffinés.
8.3) La simulation des équations de Navier Stokes
moyennées (RANS)
Les simulations RANS résolvent les équations de
Navier-Stokes moyennées. En d'autres termes, la turbulence est ici
entièrement modélisée. De ce fait, les résultats
obtenus ne sont pas toujours représentatifs de la réalité,
surtout si les configurations simulées sont complexes (en situation
réactive notamment). Toutefois ce type de simulation permet d'obtenir un
bon ordre de grandeur de l'écoulement moyen aussi bien en termes de
vitesse que de température ou de pression. C'est pour cela que beaucoup
des codes industriels actuellement sur le marché sont basés sur
ce principe. Le coût de calcul (en temps CPU) est en effet relativement
faible, ce qui permet de simuler des configurations très complexes sur
des maillages raffinés.
Le schéma suivant définit une comparaison graphique
approximative des principales simulations


Figure (2.4) : La comparaison graphique des
déférentes simulations
9) Les équations moyennées

On introduit dans les équations de Navier Stokes une
décomposition, en une moyenne et une fluctuation, d'une composante du
vecteur de vitesse ou, u ou. Celles ci peuvent
s'écrire sous la forme :
u u u (2.4)
Où u une valeur moyenne indépendante du temps et u
représente une partie fluctuante superposée à u.
Par définition, la moyenne temporelle de u est nulle, et
on peut donc écrire : u ? u
(2.5)
u ? u
(2.6)
Où représente un laps de temps suffisamment long
pour que les valeurs moyennes soient indépendantes du temps.
9.1) Quelques propriétés de la
moyenne
1' La moyenne d'une somme est égale à la somme des
moyennes :

g g
1' La moyenne d'un produit d'une fonction f par une
constante est :


Attention cela ne marche pas pour deux fonctions non
constantes:
9 g

v' La moyenne est invariant par elle-même : on tire de
cette relation et de la
précédente que : g g
v' La moyenne d'une fluctuation est nulle : u
v' Mais la moyenne du carré d'une fluctuation n'est pas
nulle: u u v' (Sauf si u )
v' On peut intervertir les opérations de moyenne et de
différentiations ~ mais
cela ne marche pas avec la dérivée
matérielle à cause du terme convectif (non linéaire). [10]
9.2) Equations de bilan moyennées au sens de Favre
Comme on souhaite obtenir des équations moyennées,
si on utilise la décomposition de Reynolds employée pour les
équations incompressibles :
|
Pour un terme comme
|
|
|
on aura :
)(
|
'~
|
|
(2.7)
(2.8)
(2.9)
(2.10)
(2.11)
|
|
|
)(
|
')
|
|
'
|
|
'
|
Et bien sur :
' = 0 ,
On constate que cette moyenne sera difficile à
utilisée en écoulement compressible en effet on souhaite que les
équations moyennées gardent la même forme. Favre donc a
définit un nouvel opérateur de moyenne (qui pondéré
par la masse) :
Þ
(2.13)
A partir de cette moyenne la partie fluctuante de sera
donnée par :
Comme la moyenne classique, l'opérateur de Favre est
linéaire, il est aussi idempotent dans le sens que :
|
Þ Þ
|
Þ
|
|
|
Þ
9
|
Þ
9
|
Þ
9
|
9
|
Þ
9
|
|
On remarque par ailleurs que
Þ
Þ
|
Þ
|
|
|
~ ~
Et
Þ
Donc
Þ
|
|
(2.15)
(2.16)
(2.17)
|
10) Equation de la continuité
L'introduction des valeurs instantanées au sens de Favre
donne,
·
·
·
(2.18)
On voit que donc que la moyenne de Favre permet de garder garde
la même forme à l'équation moyenne par rapport à
l'équation original instantanée.
11) Equation de conservation de la quantité de
mouvement
De la même façon, on introduit les valeurs
instantanée dans l'équation de la quantité de mouvement et
on obtient
~ ~ ~
Ou le tenseur de Reynolds s'écrit :
...
·
·
·
·
·
·
|
|
~ F (2.19)
|
|
|
|
(2.20)
|
U U
|
|
|
12) ( DUANOIEFIFIKAHAINFI
IEBTON111
Sa forme moyennée s'écrit :
~ Þ ~ Þ
Þ ~ ( ~ )
Ou
|
~
~ (2.21)
|
|
Þ ~ ~
|
v Þ
|
............ U U
|
(2.22)
|
|
Le terme u u
|
est dit énergie turbulente moyenne.
|
Pour l'équation d'état on aura :
(2.23)
13) Quelques modèles de la turbulence
Les équations moyennes résultantes comportent de
nouveaux termes qui traduisent la production des fluctuations des vitesses et
constituent le transfert d'un mouvement convectif dû aux fluctuations de
la vitesse. Ces nouveaux termes sont appelés les contraintes de Reynolds
( I ~ . ) . Celles-ci posent un problème de fermeture des
équations gouvernantes, dont la résolution doit passer par une
modélisation de la turbulence.
13.1) hypothèse de Boussinesq
Après qu'il fût établi
expérimentalement que les contraintes turbulentes augmentaient avec
l'augmentation de taux de déformation moyen des éléments
de fluide. Boussinesq proposa une relation entre les contraintes de Reynolds et
le taux de déformation, qui été donné par la
suite:
~ ~ ~ ~
~ ~ 3 (
) (2.24)
Où est le symbole de Kronecker et l'énergie
cinétique turbulente u u
Dans cette équation, le terme à modéliser
est la viscosité turbulente , elle est liée dans la plupart des
modèles aux structures turbulentes de l'écoulement à
l'aide d'une expression de la forme :
u l (2.25)
Ou u est la vitesse caractéristique de la turbulence et
I sa longueur caractéristique. Selon les modèles, la
viscosité peut être déterminée par une relation
algébrique, une ou deux équations différentielles.
13.2) Modèle à zéro
équation
Ce modèle de turbulence est le plus simple car celui-ci
ne fait appel à aucune équation de transport. Prandtl et
Kolmogorov ont proposé une viscosité turbulente
modélisée sur le produit d'une vitesse caractéristique U
et d'une longueur caractéristique de turbulence I :
u l (2.26)
Avec :
13.3) Modèle à une équation de
transport : Prandtl-Kolmogorov
La viscosité turbulente est déterminée comme
suite
v l (2.27)
L'énergie cinétique de la turbulence est
déterminée à l'aide d'une équation de transport, on
trouve :
1
(
) (2.28)
Donc on trouve:
v |
1 | (2.29)
13.4) Modèles à deux
équations
13.4.1) Modèle k-å
Ce modèle de turbulence est le plus utilisé en
pratique, dû à Launder et Spalding (1974). Il consiste à
introduire dans les équations de Navier-Stokes moyennées (ou
équations de Reynolds) une viscosité turbulente pour
modéliser les tensions de Reynolds et une diffusivité turbulente
pour représenter les flux turbulents de masse et de quantité de
chaleur. Cette viscosité est calculée à partir de deux
grandeurs : l'énergie turbulente par unité de masse k et la
dissipation par unité de masse. Ces deux grandeurs sont obtenues chacune
par résolution d'une équation de transport. La viscosité
turbulente :
e v ~
~ (
) (2.31)
e, sont données par les équations de transport
citées ci-dessous en n'import quel point du domaine
d'écoulement.
( )
~ ~ ~ ~
{ (2.32)
( E) ~
~ ~ ~ ~ ~ ~ ~ ~~
Et dans lesquelles le terme de production de l'énergie
cinétique turbulente , et les coefficients de diffusion et E
sont données par :
~
~
(2.33)
Et:
~~
{
(2.34)
E
~
Les coefficients du modèle sont déterminés
par l'expérience comme suit[26]:
9 E E 9 c o-E
13.4.2) Le modèle k-å RNG
Le modèle k-å RNG a été
dérivé utilisant une technique statistique appelle «
Renormalization », il contient les avantages suivants :
ü Un terme additionnel dans l'équation de (å)
qui améliore la précision des écoulements avec contraintes
rapide.
ü L'effet de tourbillonnement est amélioré
afin de croitre la précision des écoulements tourbillonnaires.
ü Prendre en compte l'effet des bas nombres de Reynolds.
ü Donc les équations de transport sont :
( )
~ ~~ ~ ~ ~
( E) ~ ~
~
~ ~ ~~ ~ ~ ~ ~~
{ (2.35)
Les coefficients et Esont les inverses du nombre de
Prandtl pour k et å
respectivement. Pour un nombre de Reynolds
élevé:
|
Þ E
E Þ E3
|
Þ ~
|
E ) ~Þ Þ (2.39)
|
( - )
E 9 , ff E E E
Avec:
~
(2.36)
{
ili = 0.012
Étant une mesure scalaire du tenseur de déformation
:
v (2.37)
Est le tenseur des taux de rotation :
((2.38) Les constantes de ce modèle sont standard [11]
:
9 E E 9 c ciE
Ces valeurs sont déterminées de l'expérience
pour étudie un écoulement cisaillées. 14)
Correction de Pope
Le modèle k-å prédit d'une manière
très correcte les configurations planes, cependant il sous estime
l'épanouissement des jets rond par environ 15%. Plusieurs auteurs on
essayés de corriger ce problème en agissant directement sur les
constantes du modèle. S. Pope a proposé une explication physique
du problème du modèle k-å, selon laquelle il remarque que
dans les écoulements axisymétriques, les tourbillons toriques qui
entourent le jet vont être étirés, ce
qui provoque un taux de dissipation plus important
comparativement au cas plan [11].
Mathématiquement, cette correction introduit un nouveau
terme source dans l'équation de qui s'écrit :
|
Þ
E
|
Þ
u ~Þ *(
Q ) ~Þ
+
|
|
Notions sur la turbulence
|
|
|
|
|
|
|
36
|
|
Avec :
Þ
Þ
Þ
|
Þ
|
Þ
~Þ
~
|
Þ
Þ
|
~
|
Þ
|
~
|
(2.40)
(2.41)
(2.42)
|
|
Þ
~Þ
~
|
Þ
|
Þ
|
~
|
|
Þ
|
|
|
|
Dans le cas d'un écoulement axisymétrique sans
prérotation, l'invariant Þ se réduit á :
~
( Þ ~Þ
Þ (~Þ Þ) ~ Þ
) (2.43)
L'étirement des tourbillons n'intervient pas dans les
écoulements plans, limitant ainsi la correction aux cas
axisymétriques seulement.
15) La fermeture du second ordre
Il est possible de dériver des équations exactes
pour les contraintes de Reynolds en prenant la moyenne temporelle (moment du
second ordre).
1 (i ) l u ) (2.44)
Où u ) est l'opérateur de Navier-Stokes c a d :
u )
au a
a a ~
~~
~
~
On utilisant la moyenne de l'équation (2.44) pour cette
dernière on obtient l'équation du transport des contraintes de
Reynolds pour un écoulement incompressible donnée par :
u E k (2.45)
k k
Avec : est la production de l'énergie cinétique de
turbulence, le terme des
contraintes de pression, e le terme du taux de dissipation et est
le terme de diffusion du
troisième ordre, ils sont donnés par
:
(2.46)
k k
|
Notions sur la turbulence
|
|
|
|
37
|
|
E
|
|
|
U
|
(2.47)
(2.48)
(2.49)
|
|
(
|
~
|
|
U
|
|
k k
|
|
U U U
|
La partie est la partie fluctuante du tenseur de contraintes. La
première partie de
est le terme de triple vitesse, il représente le
transport par la convection fluctuante. Les deux
autres termes sont de
transport de pression (la corrélation vitesse pression). On remarque
que
l'équation des contraintes de Reynolds contient une autre
inconnue d'ordre supérieur
( u ~ u ). L'équation (2.49) peut être fermée
par une formulation empirique, cela est du à la nature non
linéaire des équations de Navier-stokes.
16) Conclusion
Cette analyse du phénomène de la turbulence a
montrée les différentes approches de la simulation
numérique utilisée pour les écoulements turbulents. On a
mis en évidence les caractéristiques de l'approche RANS et le
modèle - ~~.
| 


