Conclusion
Dans ce chapitre on a vu les différents types de la
combustion et les régimes concernant la combustion turbulente
prémélangée, ainsi que l'influence de la turbulence sur la
flamme et l'effet inverse.
Le modèle utilisé est celle d'EDM qu'est simple et
est contrôlé par la turbulence pour l'hypothèse de la
chimie infiniment rapide.
CHAPITRE VI
RESULTATS DU CALCUL
NUMERIQUE
1) Dispositif expérimental
1.1) La chambre de combustion

Couvercle
Accès optique
Vérin de brûleur
Cylindre en acier
Matériel de mesure
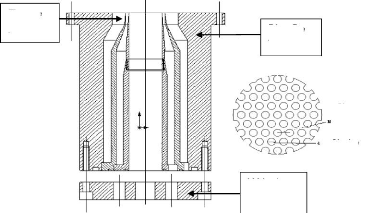
Figure (4.1) : Installation de combustion haute pression
La chambre de combustion (figure 4.1) est composée de
deux cylindres en acier, chacun a une hauteur de 600 mm et un diamètre
intérieur de 300 mm. Les deux blocs ont quatre accès optiques
circulaires de diamètre 100 mm disposés à 90°. Les
deux parties sont superposées et coiffées par un couvercle qui
récupére les condensats issus de la combustion, qui sont ensuite
évacués par une pompe. La pression est réglée par
quatre soupapes de sécurité posées sur le couvercle. A la
base de la chambre de combustion de trouve un bruleur pouvant se
déplacer verticalement car les dispositifs de mesure sont fixes. Les
accès optiques sont chauffés par des résistances
électriques afin d'éviter la condensation d'eau.
1.1) Le bruleur
C'est un tube en laiton enveloppé par un autre en acier
inoxydable, sa longueur est de 230 mm. Ce tube est muni d'une grille de
turbulence (de solidité = rapport entre la surface bloquée et la
surface totale = 51%) placée à 50 mm en amont de la sortie, afin
d'éviter les détériorations causées par les
problèmes de rentrée de la flamme. La flamme pilote est annulaire
de largeur 2 mm, elle permet de stabiliser la flamme principale lorsque le
mélange est pauvre et de compenser les pertes thermiques à la
base du bruleur. L'allumage de la flamme pilote est fait par une
électrode en cuivre (haute tension 11kv). Cette électrode ne
perturbe que très peu la flamme pilote et aucunement la flamme
principale. L'allumage de la flamme principale est réaliser par la
flamme pilote.
Flamme pilote
Distance entre 2 trous
Diamètre de trou
Vérin du brûleur
Disp. De fixation
Figure (4.2) : Bruleur de prémélangée
(gauche) et grille de tranquillisation de la turbulence (droite)
2) Modélisation de la chambre de combustion 2.1)
Géométrie de la chambre
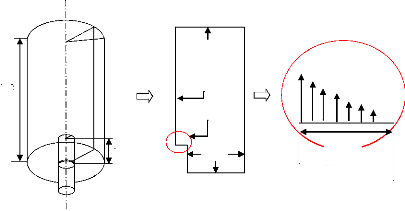
La chambre de combustion est modélisée par un
cylindre de longueur 1.2 m. l'entrée d'air se fait par un injecteur de
diamètre de 25 mm et pénétrant dans la chambre d'une
distance de 150 mm. En raison de l'axisymétrie, on considère le
problème bidimensionnel.
L=2
Sortie
Axe de
Zone
Linj=0.1 Paroi
U(m/s)
25 mm
Figure (4.3) : Géométrie détaillée de
la chambre de combustion
3) ( t7ISI-1H7X
prTq7I-1IS71jI-t1ISIBTr1t7rE7lI-Ht1ISBHT1lB1chambre de
combustion
Pour connaitre la structure de l'écoulement dans la
chambre de combustion, un premier test est fait avec un jet d'air non
réactif. Le mélange air-combustible est remplacé par la
même quantité d'air seul à température ambiante. En
effet, la proportion de méthane a richesse 0.6 ne représente que
0.4% en masse de la quantité d'air et ne change quasiment pas les
viscosités.
3.1) Conditions aux limites
Les conditions aux limites prises de l'expérience sont :
Entrée du jet principal
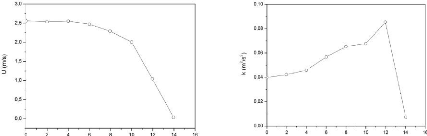
Vitesse u : (figure (4.4.1))
Energie de turbulence k : (figure (4.4.2))
Le taux de dissipation : son profile est calculé à
partir de celui de k par la relation 3/ ( P ), où P est le
diamètre hydraulique.
Sortie de la chambre
Pression de sortie : Celle de l'air ambiant, elle est prise
égale à 1 atm ou 101.3 kPa. Taux de turbulence :
L'écoulement à la sortie est établi, l'intensité de
turbulence est 1% Axe de symétrie de la chambre
On a choisis une limite de type axe de symétrie (tous les
gradients sont nuls avec vitesse v=0)
Parois solides
Les études expérimentales ont montrés que
l'effet des parois est négligeable.
|
Figure (4.4.1) : Profile de vitesse
d'entré (U)
|
Figure (4.4.2) : profile de
l'énergie
cinétique turbulente (K)
|
3.2) Maillage de calcul
La première étape du calcul réside dans
l'élaboration d'un maillage qui assure la convergence de la
procédure numérique, et qui est capable de capter toutes les
variations des paramètres dans le domaine de calcul. En plus, un
maillage doit assurer l'indépendance de la solution du raffinement
(augmentation du nombre de mailles), ce critère est dit «
indépendance maillage-solution ». Dans notre étude plusieurs
maillages ont été testés, on a choisis le maillage qui
assure ces critères avec un nombre minimal de cellules.
Le maillage de calcul élaboré est non uniforme,
il est fin dans la zone de forts gradients de vitesse (prés des parois
de l'injecteur, dans la couche cisaillée du jet). Les cellules les plus
petites sont placées sur les lèvres de l'injecteur. La figure
représente une partie du maillage à la proximité de sortie
d'injecteur. Le maillage est formé par 16291 noeuds.

Figure (4.5) : Maillage près de la zone d'injection
3.3) Calcul de l'écoulement non réactif et
ajustement de la correction de POPE L'introduction de la correction de
Pope (chapitre II) est faite par un programme externe, écrit en C++, qui
est compilé et exécuté avec FLUENT.
Mathématiquement, cette correction introduit un nouveau
terme source dans l'équation de Þ qui s'écrit (est
déjà vue dans le chapitre II) :
Þ t
Þ
~ Þ *( t
~ ) Þ
+ Þ
Þ
Þ

(4.1)
( 3 Þ -- )
Dans le cas du jet libre, le coefficient 3 9 . Dans notre cas,
et après plusieurs
calculs, on a trouvé que la valeur de 3 donne un meilleur
compromis entre les
variations axiales de l'énergie turbulence et la
vitesse.
3.3.1) Résultats du calcul
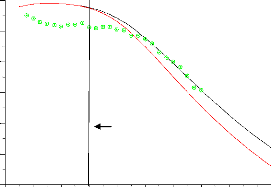
La figure (4.6) montre une comparaison entre les calculs et
l'expérience pour la vitesse u le long de l'axe. On peut dire que les
résultats sont très acceptables surtout lorsqu'on utilise la
correction de Pope. L'épanouissement du jet le long de l'axe est
très proche de l'expérimentale, la même constatation peut
être faite sur la figure (4.7) où on représente
l'énergie cinétique de la turbulence.
U
(X=0.2)
X
Calcul Exp. Calcul sans pope
Figure (4.6) : vitesse axial [m2/s2]
X
8 0.3 0.32 0
Calcul Exp. Calcul sans pope
Figure (4.7) énergie cinétique de turbulence k
[m2/s2]
3.3.2L[& Xr[SR,IQ,iIl
Une des caractéristiques les plus importantes des jets
est la longueur du coeur potentiel ou cône potentiel. Ce coeur est
crée par la décharge du jet dans la chambre de combustion ou la
vitesse est très faible (de l'ordre de 0.01 m/s). Le jet trouve la
couche de mélange et le phénomène d'entrainement qui le
font perdre sa quantité de mouvement au profit du fluide ambiant (figure
(4.8)). Cette perte se traduit par la diminution de la vitesse de jet à
sa périphérie et par une production de l'énergie de
turbulence k (figure(4.9)). A la sortie du bruleur, la zone du mélange
turbulent n'a pas d'épaisseur. Elle s'épaissit en
s'éloignant de l'injecteur et finit par atteindre l'axe ou la vitesse
axiale commence à décroitre. La zone limitée par la sortie
du brûleur et la position ou la vitesse axiale commence à
décroitre est appelée coeur potentiel.
La figure (4.6) montre le changement de pente (à x=
0.2m) indiquant la fin du coeur potentiel. Plus loin dans le jet, lorsque le
profil ne varie plus d'une section à l'autre, le jet est dit pleinement
développé.
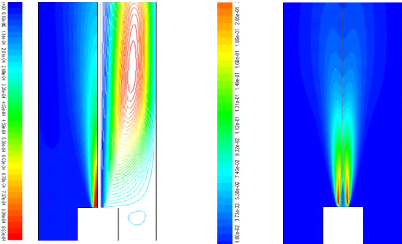
Figure (4.8) : Vitesse axiale (u) Figure (4.9) : Energie de
turbulence k
Les figures (4.8) et (4.9) montrent respectivement la
distribution de la vitesse et de l'énergie de turbulence. La vitesse est
maximale sur l'axe de symétrie, elle diminue pour
s'annuler sur les parois solides. La quantité du
mouvement introduite par le jet est transférée à
l'écoulement stagnant dans la chambre. Le mouvement tourbillonnaire dans
la chambre provoque une légère augmentation de la vitesse
à proximité des parois.
Pour l'énergie de turbulence, on remarque qu'elle est
produite essentiellement dans la zone de mélange entre le jet principal
et celui stagnant dans la chambre.
4) Calcul pour de l'écoulement réactif du
méthane-air
Après l'écoulement non réactif, on va
calculer la combustion turbulente pauvre du méthane avec valeurs
différentes de la richesse et nous conservons les autres conditions
telles que les profils de la vitesse (u) et l'énergie turbulente (k).
4.1) Les caractéristiques du mélange
(méthane/air) à l'entrée du bruleur
Nous avons comme données , la fraction massique du
combustible est donnée par :
(4.2)
Pour la réaction (méthane/air), on a
déjà calculé la valeur de s dans le chapitre I s = 4.00,
la mass molaire de N2 et O2 sont respectivement
MN2=28 (kg/mol) et MO2=32 (kg/mol).
Pour
YCH4=0.0337
Et comme
(4.3)
0
Alors
YO2=0.02243
Les fractions massiques obtenues pour les trois cas sont :
|
Richesse
|
0.6
|
0.7
|
0.8
|
|
YCH4
|
0.0337
|
0.0390
|
0.0444
|
|
YO2
|
0.2243
|
0.2231
|
0.2219
|
Tableau(4.1) : les fractions massiques obtenues pour chaque
richesse.
4.2) Résultats du calcul 4.2.1)
Richesse
Pour la richesse 0.6, on a gardé le même maillage du
cas froid. Vu l'optimisation
des constantes A et B du modèle EDM, le calcul a
convergé après 17097 itérations. L'évolution des
résidus est montrée par la figure (4.10).
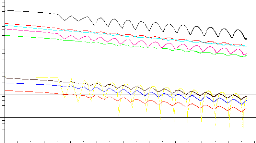
Figure (4.10) : Résidus du calcul pour une richesse de
0.6
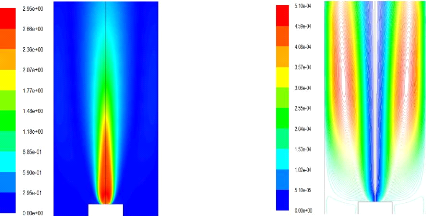
Figure(4.11) :Champs de vitesse (m/s) Figure(4.12) : Ligne de
courants
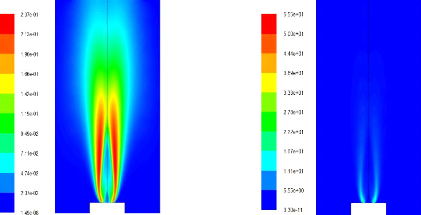
Figure (4.13) : Energie turbulent k(m2/s2)
Figure (4.14) : Taux de dissipation (m2/s3)
On montre le champ dynamique par les figures (4.11), (4.12),
(4.13) et (4.14). Les vitesses sont plus importantes que dans le cas froid,
ceci est du à l'expansion des gaz à cause de la combustion. Aussi
on remarque que l'énergie cinétique de turbulence et son
taux de dissipation qui sont plus importantes, ceci est logique
car les gradients de vitesses sont plus grands.

a ps e a e ac o
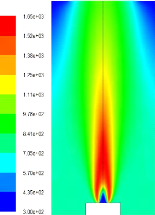
Figure (4.15) : Température (K) Figure (4.16) : Taux de
réaction ( m
m3 )
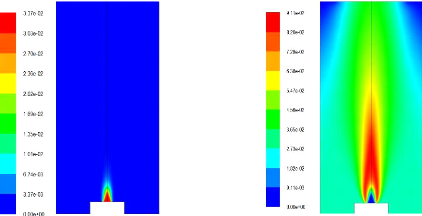
Figure(4.17) : Fraction massique du CH4 Figure(4.18) : Fraction
massique du CO2
Dans les figures (4.15, 16, 17 et 18), on montre les champs
thermiques et des espèces. La température adiabatique de la
combustion est bien reproduite par le modèle EDM, elle est de l'ordre de
1650 K (celle calculée par PREMIX [11] est 1664K). Le taux de
réaction
est principalement concentré dans la zone de
mélange car il dépend directement de l'énergie
cinétique de turbulence et son taux de dissipation. Pour les
espèces, on a présenté le combustible (CH4) et le CO2,
dès que le combustible est injecté il s'chauffe et s'enflamme
donnant le CO2 et l'H2O. La fraction massique maximale du CO2 est de l'ordre de
0.0091.
4.2.2) Pour / =0.7 :
Dans ce cas, et a cause des problèmes dans la convergence,
on a optimisé le maillage par le raffinement de la zone de
réaction.
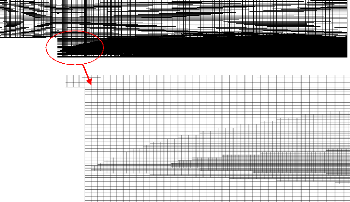
Figure (4.19) : Maillage pour le calcul dans le cas de
Le calcul prend 10 000 itérations pour converger, on
montre le cumule des résidus dans la figure (4.20).
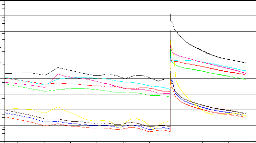
Figure (4.20) : Les résultats des calculs pour =0.7.
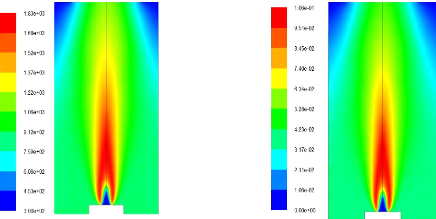
Figure(4.21) :Champs de Température Figure(4.22) :
Fraction massique du CO2
A cause de la ressemblance des résultats, sauf dans
l'aspect quantitatif, on se limite à la représentation des champs
de température et de CO2. La température atteint 1830 K, ce qui
favorise la formation des NOx thermique. La valeur maximale du CO2
est 0.1.
4.2.3) Pour ~
La convergence est obtenue après 1500 itérations
depuis de dernier calcul. Les figures (4.24 et 25) montrent le champ de la
température qui présente un maximum de 2000 K, la valeur
donnée par PREMIX est 1997K. Le CO2 atteint son maximum à une
fraction massique de 0.12.
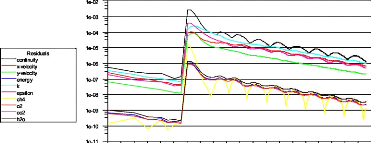
Figure (4.23) : les résultats des calculs pour
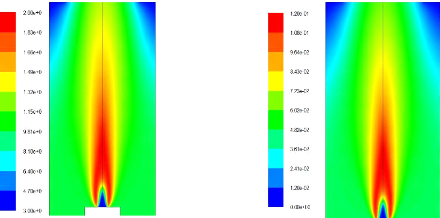
Figure(4.24) :Champs de Température (K) Figure(4.25) :
Fraction massique du CO2
Une comparaison de la variable d'avancement, calculée
en post traitement à partir de la température, est faite avec les
mesures pour les trois richesses (fig. 4.26 et 27). L'optimisation des
constantes A et B de l'EDM nous a permis d'obtenir une longueur de la flamme
très proche à celle expérimentale pour la richesse 0.6. On
a essayé de faire le même ajustement pour les autres richesses
(0.7 et 0.8) mais la température obtenue dépassait largement
celle adiabatique et la procédure numérique diverge. A notre avis
le modèle utilisé n'introduit pas les caractéristiques
physico chimiques du combustible, c'est pourquoi il ne donne pas une bonne
longueur de la flamme. Cette dernière est le résultat de la
compétition entre la vitesse d'injection et celle de la flamme
turbulente.

Figure (4.26) : Contours de la variable d'avancement c
calculée pour les trois richesses.

Figure (4.27) : Contours de la variable d'avancement c
mesurée pour les trois richesses.
5) Structure interne de la flamme
Pour représenter les propriétés
calculées on a pris trois stations ou coupes transversales et une
longitudinale le long de l'axe de symétrie dans le domaine de calcul. La
première station est à une hauteur h/3 de la hauteur de la
flamme, la deuxième est à 2h/3 et la troisième est
à h (figure 4.28).
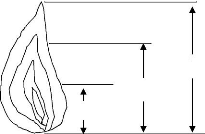
h
2h/3
h/3
Figure (4.28) : Différentes stations représentation
sur la flamme
On compare la variable d'avancement post traitée à
partir de la température avec cette mesurée sur l'axe de
symétrie. On voit le bon accord entre les deux courbes.
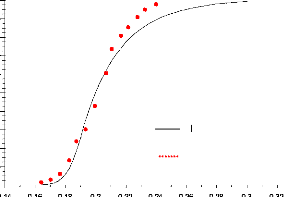
Numérique Expérimentale
X
Figure(4.29) : Variable d'avancement le long de l'axe pour une
richesse de 0.6.
On a comparé aussi les propriétés sur les
trois plans de coupe dans la flamme de richesse 0.6. On remarque la
distribution de la température sur ces stations qui est égale
à celle de l'injection (300K) sur le cône potentiel, elle augmente
au fur et à mesure qu'on monte dans la flamme et lorsqu'on se dirige
vers le front de la flamme ou le gaz se réchauffe et s'enflamme. Ceci
est traduit par les courbes des vitesses, de l'énergie cinétique
de turbulence et du taux de réactions qui présentent les
mêmes variations. En résumé dès qu'on s'approche du
front de flamme, on na expansion des gaz et par la suite augmentation de la
vitesse et production de l'énergie cinétique de turbulence.
h/3 2h/3 h
|
T
|
|
|
k
|
|
|
|
|
|
Y
|
|
Y
|
|
|
Figure(4.30) Variation de la Température (K) dans les
016 018 02 022 024 026 028
trois stations
Pit
|
2Figure(4.31) : Variation d'énergie turbulente
k
(m2/s2) dans les trois stations
|

|
U
|
|
|
|
|
Yi
Y
|
|
|
Y
|
|
Figure(4.32) : Variation de la vitesse (m/s) dans les
trois
stations
|
Figure(4.33) : Variation de taux de réaction
(
m
) dans les trois stations
m
|
|
( m ) O2/3 CH4 H2O CO2
|
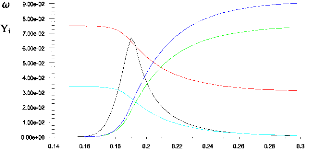
x
Figure (4.34) : Structure de la flamme pour une richesse de
0.6
Sur la figure (4.34), on montre la structure interne de la
flamme, on voit bien que le combustible et le comburant réagissent pour
donner les produits de réaction avec un taux de réaction maximal
au front de la flamme.
= 0.6 0.7 0.8

x
Figure (4.35) : Fraction massique du CO2 sur l'axe pour les trois
richesses
La figure (4.35) montre l'évolution axiale de la
fraction massique du CO2 pour les richesses 0.6, 0.7 et 0.8. On remarque que la
production de ce gaz à effet de serre augmente avec la richesse en
régime pauvre. Ce résultat est logique car on augmente la
quantité de combustible et par conséquent celle du carbone.
| 


