IV. 4. 3. ANALYSE COMPARATIVE
DES PARAMÈTRES PLUIES ET EVAPORATIONS
IV. 4. 3. 1. PRESENTATION BRUTE
DE LA SERIE
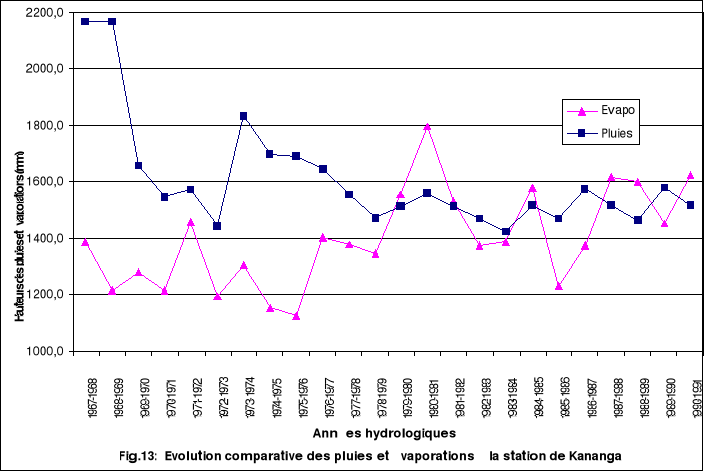
Ce graphique couplé pluies et évaporations
semble être difficile à analyser. Leurs analyses
séparément ont montré que l'une avait la tendance à
la baisse et l'autre avait la tendance à la hausse. Il y a quelques
années ou les deux paramètres corroborent très bien et
d'autres ou elles sont en discordance totale. Nous pouvons les remarquer
en1971-1972 ; 1972-1973 ; 1975-1976 ; 1983-1984 ou elles sont en
discordance totale et en 1976-1977 ; 1977-1978 ; 1977-1978 ;
1980-1981 ; 1987-1988 ou elles sont en parfaite corrélation.
Comme nous nous retrouvons devant deux situations
contradictoires, nous faisons appel à un test statistique
décisionnel, pour être au moins concret dans la prise des
décisions,
Nous utilisons ici, le fameux test de corrélation de
Bravais - Pearson, pour décider sur la linéarité ou pas
de l'évolution de ces deux paramètres.
IV. 4. 3. 2. TEST DE
CORRELATION DE BRAVAIS - PEARSON
Sur un échantillon de 24 ans seulement à la
station météorologique de Kananga ou les deux paramètres
se retrouvent sur une série continue de prélèvement durant
les mêmes périodes, nous pouvons calculer l'écart type, la
covariance et ensuite le coefficient de corrélation de ces deux
paramètres ;
COV(x,y) =  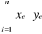 et rx,y = et rx,y = 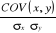
La moyenne de la série des pluies 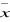 = 1592,1mm = 1592,1mm
La moyenne de la série des évaporations 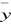 = 1400,1mm = 1400,1mm
L'écart type de la série des pluies
óx = 150,5mm
L'écart type de la série des évaporations
óy = 171,1mm
COV(x,y) =  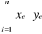
COV(x,y) = 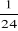 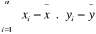 = -7423,4mm = -7423,4mm
rx,y = 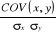
rx,y = 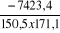 = - 0,3 = - 0,3
Pour trancher sur la linéarité ou pas de la
corrélation entre les pluies et les évaporations à la
station de Kananga, voyons ce que le test va nous donner comme résultat
:
tc = 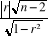
avec (n-2) : degré de liberté
tc : valeur calculée du
test qui représente Ho
r : coefficient de corrélation
r2 : coefficient de
détermination
n : effectif
tc = 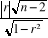 = = 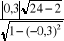 = 1,4071247/0,9539392 = 1,4720675 = 1,4071247/0,9539392 = 1,4720675
Au seuil á qui n'a que 5% de chance de se tromper, on
peut calculer la valeur tabulée H1 :
tt(0,05 ; n-2)
tt (0,05 ; 22) = 0,4044
La valeur calculée étant supérieure
à la valeur tabulée, l'hypothèse nulle (Ho) est
rejetée et on retient alors l'hypothèse alternative
(H1) (tc > tt). Ceci confirme les analyses
faites plus haut sur la figure13 qu'il y a la majorité des années
de discordance primant sur les années où il y a quelques
corrélations entre les deux paramètres.
| 


