Etude des erreurs se trouve ainsi au centre de la
qualité de la représentation, aussi bien dans le cas des
coefficients de détermination et de corrélation que celui de
l'analyse de la variance (Test de Ficher).
a)
Lois des écarts
La loi des écarts permet de relier l'erreur
associée à l'hypothèses nulle et l'erreur associée
à l'hypothèse alternative « Y dépend de
X ». L'erreur attachée à l'hypothèse nulle est
mesurée par la dispersion totale des Yi par rapport à la moyenne
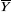
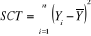
L'erreur attachée à l'hypothèse
alternative appelée « erreur résiduelle » est
donnée par la somme des carrés des écarts entre les
observations Yi et les valeurs estimées ... par le
modèle s'agit là de l'erreur associée au modèle
notée 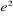
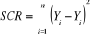
La différence entre la dispersion totale et la
dispersion résiduelle correspond à la dispersion explique par le
modèle de régression.
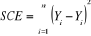
De ces relations, nous pouvons donc déduire
l'équation fondamentale d'analyse de la variance. 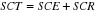 .La variabilité totale (SCT) est égale à la
variabilité expliquée (SCE) plus la variabilité des
résidus (SCR). .La variabilité totale (SCT) est égale à la
variabilité expliquée (SCE) plus la variabilité des
résidus (SCR).
b) Coefficient détermination
Un premier indicateur de qualité de la
représentation consiste à mettre en relation la dispersion
expliquée par le modèle et la dispersion totale des
données. Le coefficient de détermination R2 mesure le
pouvoir explicatif du modèle en évaluant le pourcentage de
l'information restituée par le modèle par rapport à la
quantité d'information initiale.
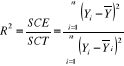
c) Test de Ficher
Ce test appelé analyse de la variance, permet
d'intégrer la taille de l'échantillon dans l'appréciation
de la qualité de la représentation.
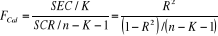
Où K est le nombre de variables explicatives du
modèle.
Cette valeur doit être comparée à celle
qui est lue dans la table de Ficher pour k degré de liberté au
numérateur et n-k-1 degré de liberté au
dénominateur à un seuil donné.
Si Fcal > Ftable, on conclut que le
modèle est globalement explicatif et on adopte H1,
l'hypothèse selon laquelle le modèle est explicatif.
Le tableau ci-après présente l'analyse de la
variance pour un modèle de régression simple.
Tableau n°1. Analyse de la variance
|
Source de variation
|
Degré de liberté
|
Somme des carrés
|
Carrés moyens
|
F calculé
|
|
Régression
|
K = 1
|
SCE
|
|
|
|
Résidu
|
n-k-1
|
SCR
|
|
|
Total
|
n-1
|
SCT
|
-
|
|
F Table
|
F&, k, n-k-1
|
II.1.4. TESTS ET INTERVALLES DE CONFIANCE DES PARAMETRES DE
REGRESSION
a) Tests de signification des
paramètres
Les tests précédents permettent d'avoir une
idée de la validité de la régression dans son ensemble. Il
importe de connaître également la validité des
paramètres estimés afin que ces derniers soient
interprétables. Cette validité est vérifiée par le
biais du test T de Student.
Ainsi, il s'agit de tester l'hypothèse selon laquelle
les paramètres estimés sont statistiques différent de
zéro. Pour ce faire, on pose l'hypothèse que chaque
paramètre est nul, indépendamment des autres, à l'aide de
la distribution de Student à (n-2) degré de liberté.
L'hypothèse alternative est une valeur positive ou négative,
selon le paramètre concerné par le test.
Les hypothèses sont donc formulées de la
manière suivante :
On tester HO : 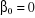 contre H1 : contre H1 : 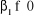 ou ou 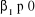
Si la statistique TCal sur le paramètre est
supérieur, en valeur absolue, à la statistique TTable
de Student, on rejette l'hypothèse nulle. Cela veut dire que le
coefficient est statistiquement significatif.
Le calcul de T associé aux paramètres se fait
par la formule :
ü Pour â0, 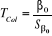 avec avec 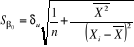
ü Pour â1, 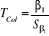 avec avec 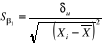
L'estimateur sans biais de l'écart-type de l'erreur
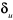 est obtenu par la formule : est obtenu par la formule : 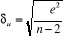
| 


