III.3 ETUDE DE CAS
Un revendeur d'huiles industrielles se réapprovisionne
chaque mois et reçoit son réapprovisionnement dans un
délai d'un mois. Sa capacité de stockage s et connait les
coûts de stockage par tonne par mois C1, le
coût de pénurie par tonne par mois C2 et le
coût supplémentaire de stockage par tonne, lorsque la
capacité s est dépassée C3.
1. Q est quantité égale au montant de la
commande majoré de la quantité existant en stock, au moment de la
passation de la commande ;
Si P(x) est la densité de probabilité de la
demande mensuelle ; Calculer le coût total CT(q), et en déduisant
la formule permettant de calculer la valeur de q correspondant au coût
minimal.
2. On a les valeurs des coûts suivantes : C1
= 100$ ; C2 = 1000$; C3 = 500$ ;
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

35
Calculer les valeurs optimales de q pour E ??i
5 ??=1 ; en supposant
que p(??) =
??????-??x
????(??+1)
Et en sachant que la variance et la moyenne valent 2.
?? ??+1
RESOLUTION DU PROBLEME
Soient x et y sont des demandes de la clientèle pour 2
mois consécutifs.
Nous observons 3 cas dans ce problème : nous aurons a
calculez les stocks et les pénuries moyens dans chacune des cas :
1) q - y > s : dans ce cas il y aura un
excèdent en stock. La quantité excédentaire ?? - ?? -
?? subit le coût ??3 par tonne au début
du second mois, on aura un stock s.

q-y
x
a) ??= ??
s
Stock moyen Stock fin

Stock moyen
Stock fin
1 2
t
Coût : CT = c1 * (??-
x2) + c3 * (??- ??- ??)
b) ??> ??
2
??2
t
1
??1
q-y
s
x
Penurie moyenne
|
On a ??
??1
|
= ?? ; t1 = ?? ; t2 = 1- ?? avec
un stock moyen pendant
x x
|
t1 = Z et une pénurie moyenne pendant
t2 = xZ ?? ; et le coût
x-?? * x-??
*
+ c3 * (??- ??- ??)
2 x 2 x
total ???? = c1 * ?? * ?? c2
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

36
2) 0 = ?? - ?? = ?? : au début du second mois la
quantité ?? - ?? sera en stock.
a) ??= ??- ??

Le stock moyen pendant la période ??- ??- ??2
q-y
x
Stock moyen
Stock fin
1 ?? 2 t
???? = ??1 * (??- ??- 2)

s
a) ??> ??- ??
q-y
Stock moyen
1
x
??1
??2
2
On a donc ??-??
??1
= ??; ??1 = ??-??
?? ??2 Penurie??
??-??
moyenne
;
Stock moyen pendant ??2 = ??-??+??
2
?? - ?? ?? - ??+ ??2 * (?? - ?? + ??
2 ) * (?? - ?? + ??
????= ??1 * 2 * ?? )
??
3) ?? - ?? < 0 : au début du second mois on sera en
pénurie ;
1
2 t
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

37
La pénurie moyenne pendant la période est : ??2 -
?? + ??
????= ??2 * (??2 + ??- ??)
Sur n'importe quel période on aura :
??
????(??) = ? - ??? ??(??)??(??)(??1 * (?? -
2) + ??3 * (?? - ?? - ??)) ??(??)??(??)
??=0 ??=0

??=0 ??=??
+ ?
??-??
= ? ? ??(??)??(??) ??1 * (?? - ?? - ??
??
2)
??=??-??
??=0
???? ????

?? 8 ??(??)??(??)??1 * ((??- ??)2
??=??-?? ??=??-??
+ ? ?
+ ? ? ??(??)??(??) ??2 * (??
8 8
2 + ??- ??)???? ????
??=?? ??=0
Sachant que si É(??) = ? ??(??, ??)????:
??
??
??É = ? ????
?? ???? + ??(??, ??) ????
???? - ??(??, ??) ????
????
???? ????
??
Ce qui peut s'écrire, lorsqu'il s'agit
d'intégration doubles :
?? ?? ??
?? = ? ??(??) (? ??(??)?? (??, ??, ??)???? ) ???? = ?
??(??)[??(??, ??, ??) - ??(??, ??, ??)]????
?? ?? ??
??
=
?Ö(??, ??)???? ??
???? = ? ??Ö
Donc ?? ???? + Ö(??, ??) ????
?? ???? ? Ö(??, ??) ????
????
???? ????
Afin de restreindre les calculs, on constate que si l'on
intervertit l'ordre des intégrations, seules les 3???????? et
4???????? intégrales de CT(q) ont des limites en x par rapport à
q et qu'alors :
??-?? ? ??(??)??(??)(??1 * ??2
8 (?? - ??)2
2?? + ??3 2?? + ??2(?? - ?? - ??)????????
2?? + ??2 * (?? - ?? + ??)2
2?? ) ???? ????
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

38
Ö(??, ??) ????
???? ? Ö(??, ??) ????
????
= ? ??(??) ??1 * (?? - ?? - ?? - ??
?? 2 )????- ? ??(??) ??1 * (?? - ??)2
??
????= 0
2(?? - ??)
??-?? ??-??
Et dans ces conditions on aura :
??-??
?????? = (??2 + ??3) ? ??(??)???? -
??2
????
0
8 + (??1 + ??2) ?
??(??)(?0??-??
??(??)???? + (?? - ??) ???
??(??) ????)????
??-?? ??-??
On doit déterminer q tel que ??????
???? = 0. Or ?? (??) = ????-??, dont ?? = 2 ???? ?????? = 2
Ainsi, on obtient la valeur de q tel que :
??-??
(??2 + ??3) ? ????-?????? - ??2
+ (??1
0
?? ??-?? ?? 8
+ ??2) (? ????-?? ? ????-?? ???? ???? + ? ????-??(??
- ??) ? ??-?????? ???? ) = 0
??-?? 0 ??-?? ??-??
Sachant que :
? ????-?????? = -??-??(1 + ??) + ??, ? ??-?????? =
-??-?? + ?? Où ??,?? sont
constante d'intégration.
On aura :
??3???? = ?? [???? (??3 - ??1)
+ (??1 + ??2)(1 + ??)] + ????(1 -
??)(??3 - ??1) + (??1 + ??2)
A partir de la formule ci-haut nous pouvons maintenant trouver
:
??3 - ??1 = 400; ??1 +
??2 = 1100; ??3 = 500; (???? ???????????? ??????????????
?????? 100),
On a : ??3 - ??1 = 4; ??1 +
??2 = 11; ??3 = 5
Avec ?? = 2,72; ??2 = 7,39; ??3 = 20,09 ;
??4 = 54,60; ??5 = 148,41 Calculons alors les valeurs
optimales de q :
2
?? = 1; 5???? = ??[2,72 (4) + (11)(1 + 1)] + 2,72 (1 - 1)(4) +
(11)(1 - 2 )
5???? = 32,88 ?? + 5,50
2
?? = 2; 5???? = ??[7,39 (4) + (11)(1 + 2)] + 7,39 (1 - 2)(4) +
(11)(1 - 2 )
5???? = 62,56 ?? - 40,56
2
?? = 3; 5???? = ??[20,09 (4) + (11)(1 + 3] + 20,09(1 - 3)(4) +
(11)(1 - 2 )
5???? = 124,36 ?? - 199,22
2
?? = 4; 5???? = ??[54,60(4) + (11)(1 + 4] + 54,60 (1 - 4)(4) +
(11)(1 - 2 )
5???? = 273,4 ?? - 732,2
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

39
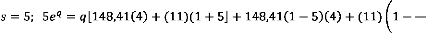
52
2
5???? = 659,64 ?? - 2501,56
Une méthode de résolution graphique est
utilisée. Comme chaque droite a deux intersections avec l'exponentielle,
il importe de noter que CT n'a pas de minimum pour q<s, entre q et s. Pour
le voir, reprendre la valeur de CT(q) lorsque q<s, c'est-à-dire que
:
? ? ??(??) ??(??) ??1 (??- ??- ??
?? ??-?? (?? - ??)2 (??- ??+ ??)2
?? 8
2)???? ????+ ? ? (??1 2?? + ??2 2?? )
????????
0 0 0 ??-??
+ ? ? ??(??)??(??)??2 (??
88
2 + ?? - ??)????????
?? 0
1 2 3 4 5 q
Le minimum est atteint pour la deuxième valeur de q
(q>s) :
??1 = 3,10; ??2 = 3,60; ??3 =
4,20; ??4 = 4,70; ??5 = 5,30
??
????
??
-
-
= 5; 5
=
[148,41(4) + (11)(1 + 5] + 148,41(1
5)(4) + (11) 1
DEBATALA Archange | TRAVAIL DE FIN DE CYCLE l

40
| 


