43
CHAPITRE II : ETUDE PRATIQUE DE L'INFILTRATION
II.1 : Etude de l'avancement
II.1.1 : Mesure de l'avancement
Les jalons ont été placés avant
l'arrosage et sont distants de 2m ; c'est-à-dire :
x0=0m ; x1=2m ; x2=4m ; x3=6 m ; x4=8m ; x5=10m ;
x6=12m.
En cours d'arrosage, on note à l'aide d'un
chronomètre les temps de passage tn aux
abscisses xn à partir du début
de l'arrosage.
Les temps de passage au niveau des différents
jalons sont consignés au tableau
suivant :
Tableau 9 : Mesure de l'avancement
xn
(m)
|
Temps d'avancement (min)
|
|
Irrigation n° 2
|
|
Raie B
|
Raie C
|
Raie D
|
Raie A
|
Raie B
|
Raie C
|
Raie D
|
|
Q=0.4l/
s
|
Q=0.6l/
s
|
Q=0.8l/
s
|
Q=0.2l/
s
|
Q=0.4l/
s
|
Q=0.6l/
s
|
Q=0.8l/
s
|
2
|
0.38
|
0.23
|
0.14
|
0.10
|
0.30
|
0.18
|
0.20
|
0.13
|
4
|
0.85
|
0.60
|
0.42
|
0.28
|
0.93
|
0.47
|
0.45
|
0.35
|
6
|
1.32
|
0.98
|
0.62
|
0.42
|
1.40
|
0.77
|
0.60
|
0.57
|
8
|
2.53
|
1.68
|
0.98
|
0.68
|
2.12
|
1.77
|
0.87
|
0.90
|
10
|
4.78
|
2.88
|
1.58
|
1.12
|
3.48
|
1.93
|
1.40
|
1.18
|
12
|
7.25
|
4.83
|
2.92
|
1.95
|
5.28
|
2.62
|
2.13
|
1.45
|
Tap
p
|
8.75
|
6.33
|
4.42
|
3.45
|
6.78
|
4.12
|
3.63
|
2.95
|
|

44
II.1.2 : Détermination de la loi d'avancement
Deus types de loi d'avancement sont
généralement utilisées en irrigation à la raie
à débit constant :
- La loi de type puissance : c'est la loi la plus
courante
X(t) = p
. t ou
r
T(x) =
a.x
b
Avec : t : temps d'avancement à l'abscisse x, en
min ; p, r, a et b : coefficients d'ajustement.
- la loi de SCS (Soil Conservation Service) de type
:
g.x
( 1 / 2 )
.
t x =
( ) . Qo S
x e (50)
f
Avec : Qo : débit d'apport au niveau de
l'unité d'arrosage, en l/s ; S : pente de la raie, en m/m ;
x : abscisse qui est atteinte par l'eau durant
tx
45
g et f sont des constantes qui dépendent de la
texture du sol.
La détermination de la loi d'avancement consiste
à ajuster les mesures de terrain à
l'une des deux lois citées
précédemment.
Dans le cas de notre expérimentation, nous avons
utilisé la loi de type puissance. Pour
faire cet ajustement, les méthodes
utilisées ont été :
- La méthode des deux points
- La méthode de régression
log-linéaire
Après application des deux méthodes, nous
avons obtenus les résultats illustrés au
tableau suivant :
Tableau 10 : Détermination de la loi
d'avancement par les deux méthodes (Méthode des deux points et
méthode de régression log-linéaire)
Irrigation n°
|
Débit
(l/s)
|
Raie
|
Méthode des deux points
|
Méthode de régression
log-linéaire
|
|
b
|
T(x) =
a.x b
|
a
|
b
|
r
|
b
T(x) =
a.x
|
01
|
0.2
|
A
|
0.016
|
2.457
|
2 , 457
T ( x ) =
0.0 1 6 x
|
0.066
|
1.790
|
0.97
|
1 ,790
T ( x ) =
0.066 x
|
|
B
|
0.016
|
2.301
|
T(x) =
0.0 1 6x
|
0.042
|
2 , 30 1
1.783
|
0.98
|
1,783
T(x) =
0.042x
|
|
C
|
0.011
|
2.236
|
T(x) =
0.0 1 1x
|
0.027
|
2 , 236
1.849
|
0.97
|
1, 849
T(x) =
0.027x
|
|
D
|
0.008
|
2.215
|
T(x) =
0.008x
|
0.023
|
2 , 2 15
1.934
|
0.99
|
1, 934
T(x) =
0.023x
|
02
|
0.2
|
A
|
0.045
|
1.915
|
1, 9 1 5
T ( x ) =
0.045 x
|
0.158
|
1.513
|
0.97
|
1 ,5 1 3
T ( x ) =
0. 1 5 8 x
|
|
B
|
0.032
|
1.766
|
T(x) =
0.032x
|
0.068
|
1, 766
1.422
|
0.98
|
1, 422
T(x) =
0.068x
|
|
C
|
0.023
|
1.828
|
T(x) =
0.023x
|
0.102
|
1 , 828
1.207
|
0.98
|
T(x) =
0. 1 02x1, 207
|
|
D
|
0.051
|
1.347
|
T(x) =
0.05 1x
|
0.032
|
1, 347
1.526
|
0.98
|
1,526
T(x) =
0.032x
|
|
46
L'évolution de l'avancement le long de la raie en
fonction du temps est représentée par les graphes suivants
:
47
Figure 7 : Courbes d'avancement ajustées par les
deux méthodes (Irrigation N°
1)
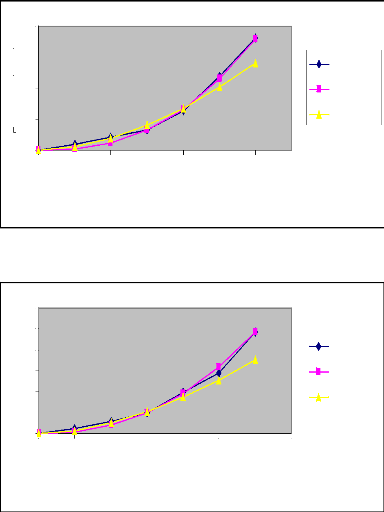
Raie B (Q=0.4l/s)
6
5
Tem O s ( m n )
4
3
2
1
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
8
Tem O s ( m n )
6
4
2
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log_lin
Raie A (Q=0.2l/s)
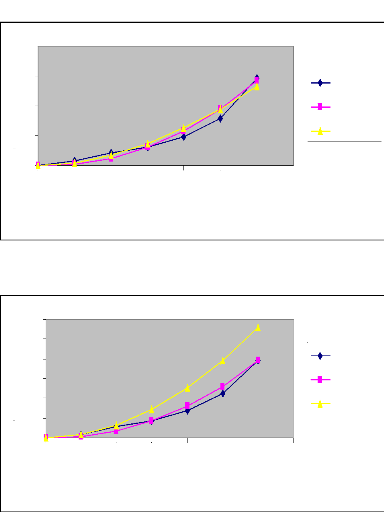
Raie C (Q=0.6l/s)
Raie D (Q=0.8l/s)
4
Tem p s (m n )
3
2
1
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
3
2,5
Tem p s (m n )
2
1,5
1
0,5
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
48
49
Figure 8 : Courbes d'avancement ajustées par les
deux méthodes (Irrigation N°
2)
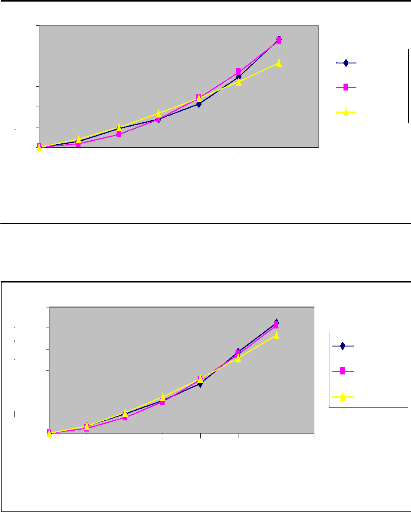
Raie B (Q=0.4l/s)
3
2,5
Tem p s (m i n )
2
1,5
1
0,5
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
6
5
Tem p s ( m n )
4
3
2
1
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
Raie A (Q=0.2l/s)
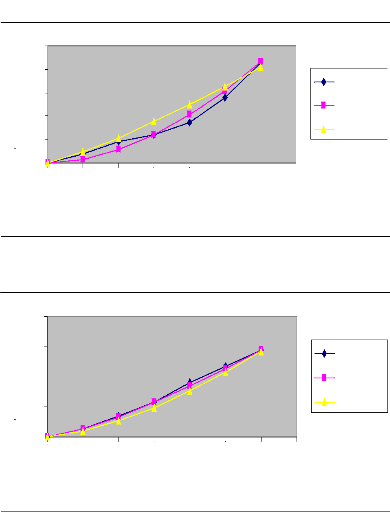
Raie C (Q=0.6l/s)
Raie D (Q=0.8l/s)
2
Tem p s (m n )
1,5
1
0,5
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
2,5
Tem p s (m i n )
2
1,5
1
0,5
0
0 2 4 6 8 10 12 14
Longueur (m)
exp
deux points log-lin
50
Tem p s (m n )
8
4
2
6
0
0 2 4 6 8 10 12 14
Longueur (m)
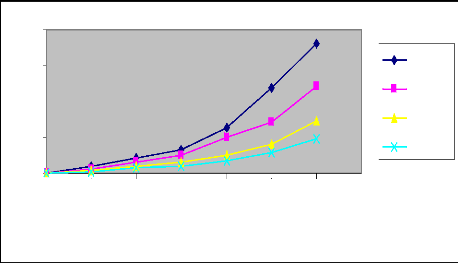
Q=0 2l/s Q=0 4l/s Q=0 6l/s Q=0 8l/s
51
Commentaire
En procédant à une analyse comparative
des courbes d'avancement des deux irrigations au niveau des mêmes raies
avec les mêmes débits, nous constatons que le temps d'avancement
diminue de la première irrigation à la deuxième
irrigation. Nous déduisons donc que l'eau s'écoule plus
rapidement sur un terrain humide que sur un terrain sec. En effet,
l'humidité du sol augmente à chaque irrigation sur la même
raie. Par ailleurs, nous constatons que la méthode des deux points donne
des résultats plus proches de ceux expérimentaux que la
méthode de régression log-linéaire.
Pour obtenir l'évolution du temps d'avancement
en fonction de la longueur de la raie, nous avons tracé le graphe
suivant qui donne le temps d'avancement en fonction de la longueur de la raie
pour les différents débits utilisés et pour les deux
irrigations.
Figure 9 : Courbes de l'évolution du temps
d'avancement en fonction de la longueur de la raie pour les différents
débits (Irrigation N° 1)
52
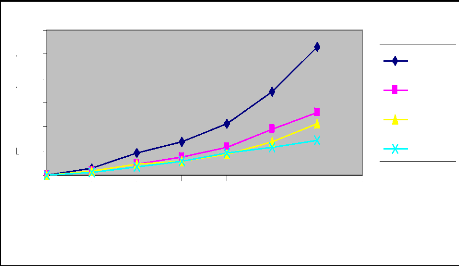
Figure 10 : Courbes de l'évolution du temps
d'avancement en fonction de la longueur de la raie pour les différents
débits (Irrigation N° 2)
Tem i s (m n )
5
4
3
2
6
0
1
0 2 4 6 8 10 12 14
Longueur (m)
Q=0 2l/s Q=0 4l/s Q=0 6l/s Q=0 8l/s
Commentaire
L'analyse comparative des différents
débits au niveau des deux irrigations nous amène à
conclure que le temps d'avancement décroît avec le débit
d'apport.
| 


