CHAPITRE III : LA MODELISATION
La modélisation est un processus qui vise
à optimiser le temps d'arrosage avec la quantité d'eau
infiltré. Il s'agit en fait d'obtenir le meilleur couple
avancement-infiltration, pour une irrigation économique, rapide et
à rendement optimum.
Pour réduire l'écart entre les
résultats expérimentaux et théoriques, nous avons
élaboré un modèle qui donnerait un compromis entre les
deux résultats.
La modélisation que nous faisons, a pour but de
rapprocher le plus possible la courbe modèle de la courbe
expérimentale ; autrement dit réajuster la loi d'ajustement.
C'est dans cet objectif que nous utilisons un mini-programme « Quick basic
» qui se résume par les étapes suivantes :
- Nous fixons « K » et nous faisons varier
« C » jusqu'à obtenir un volume infiltré modèle
I(t)mod proche du volume infiltré expérimental
I(t)exp. On note C=Cm.
- Nous fixons « C » à «
Cm » et nous faisons varier « K » jusqu'à
obtenir un volume infiltré modèle I(t)mod proche du
volume infiltré expérimental I(t)exp. On note
K=Km.
L'équation modèle s'écrira alors de
la manière suivante :
I t
( ) mod = m . +
0 . (59)
K t Cm f
t
L'algorithme utilisé est schématisé
par l'organigramme suivant :
Figure 18 : Schéma de l'organigramme
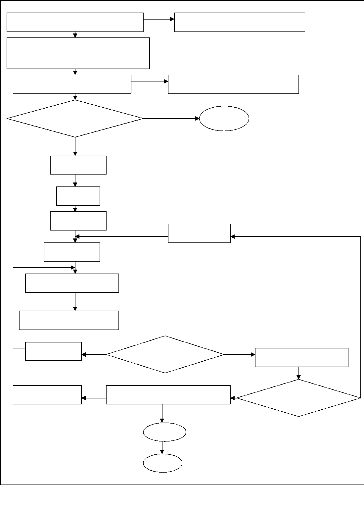
Courbe expérimentale I(t)exp
Expérimentation : I (t) exp. = f (t)
Equation de KOSTIAKOV modifiée I(t) =
K.tc + f0.t
Calcul de K, C et f0
Courbe calculée I(t)= K.te +
f0.t
Oui
I(t) cal = ? I(t)exp Fin
Non
Modèle
f0 = ?
Choix de K
Autre K
Choix de C
Choix de tc [0,...,tn]
I(t)mod = Km. tcm + f0.
t
Non
Oui
Autre C
I(t)mod = ? I(t)exp
I(t)mod = Km.tcm + f0
.t
Oui
non
Courbe modèle
Imprimer I(t)mod = Km.tcm +
f0.t
I(t)mod = ? I(t)exp
Stop
Fin
76
77
Sur la base de l'organigramme précédent,
nous avons obtenu les résultats suivants : Tableau 19 : Les nouveaux
paramètres d'ajustement Km et Cm
|
Irrigation
|
Raie
|
Débit (l/s)
|
Km
|
Cm
|
f0
|
I K t Cm f t
= m . +
0 .
|
|
01
|
A
|
0.2
|
17.68
|
0.61
|
0.68
|
I = 1 7.68t0,6
1 + 0.68t
|
|
B
|
0.4
|
4.27
|
1.14
|
1.05
|
I = 4.27t 1, 1 4
+1.05t
|
|
C
|
0.6
|
18.52
|
0.78
|
1.50
|
I = 1 8.52t0,
78 + 1.50t
|
|
D
|
0.8
|
19.25
|
0.79
|
1.40
|
I = 1
9.25t0,79 +
1.40t
|
|
02
|
A
|
0.2
|
9.05
|
0.80
|
0.56
|
I = 9.05t0,
80 + 0.56t
|
|
B
|
0.4
|
3.14
|
1.12
|
0.50
|
I=3. 1 4t1 . 1
2+0.50t
|
|
C
|
0.6
|
5.43
|
1.21
|
0.88
|
I = 5.43t 1 .2 1
+ 0.88t
|
|
D
|
0.8
|
12.27
|
0.91
|
0.89
|
I = 1 2.27t0, 9 1
+ 0. 89t
|
Les volumes infiltrés modèles
calculés à base des nouveaux paramètres Km et
Cm à l'aide de la loi de KOSTIAKOV modifiée sont
donnés dans les tableaux suivants :
Tableau 20 : Volumes infiltrés modèles pour
les différents débits (Irrigation N°
1)
Raie A : Q=0.2l/s
|
T (mn)
|
7.25
|
8.75
|
10.15
|
10.82
|
12.80
|
14.02
|
14.87
|
15.84
|
|
Vi exp (l)
|
67.58
|
71.70
|
79.36
|
84.49
|
89.62
|
94.74
|
96.03
|
105
|
|
Vi théo (l)
|
60.74
|
69.25
|
76.82
|
80.34
|
90.38
|
96.34
|
100.42
|
105
|
|
Vi mod (l)
|
64.13
|
72.34
|
79.58
|
82.93
|
92.43
|
98.04
|
101.86
|
106.12
|
Raie B : Q=0.4l/s
|
T (mn)
|
4.83
|
6.33
|
7.56
|
10.51
|
18.54
|
20.18
|
20.53
|
20.99
|
|
Vi exp (l)
|
77.46
|
80.13
|
98.07
|
108.33
|
126.95
|
135.26
|
144.23
|
151.92
|
|
Vi théo (l)
|
18.98
|
27.63
|
35.42
|
56.39
|
126.95
|
143.45
|
147.05
|
151.83
|
|
Vi mod (l)
|
30.78
|
41.64
|
50.79
|
73.42
|
138.61
|
152.42
|
155.39
|
159.29
|
78
Raie C : Q=0.6l/s
|
T (mn)
|
2.92
|
4.42
|
6.48
|
6.70
|
10.72
|
11.58
|
12.58
|
13.34
|
|
Vi exp (l)
|
60.25
|
79.63
|
92.46
|
102.71
|
130.92
|
138.89
|
145.02
|
159.12
|
|
Vi théo (l)
|
40.94
|
52.29
|
83.46
|
85.99
|
130.92
|
140.28
|
151.07
|
159.21
|
|
Vi mod (l)
|
47.10
|
65.66
|
89.27
|
91.70
|
133.89
|
142.49
|
152.34
|
159.73
|
Raie D : Q=0.8l/s
|
T (mn)
|
1.95
|
3.45
|
5.23
|
5.50
|
10.51
|
11.17
|
11.74
|
13.58
|
|
Vi exp (l)
|
32.06
|
57.91
|
80.96
|
96.37
|
134.83
|
141.24
|
147.14
|
165.60
|
|
Vi théo (l)
|
35.00
|
55.19
|
76.99
|
80.16
|
134.79
|
141.56
|
147.34
|
165.66
|
|
Vi mod (l)
|
35.35
|
57.44
|
78.45
|
81.71
|
138.16
|
145.17
|
151.17
|
170.16
|
Tableau 21 : Volumes infiltrés modèles
pour les différents débits (Irrigation N°
2)
Raie A : Q=0.2l/s
|
T (mn)
|
5.28
|
6.78
|
8.00
|
8.76
|
10.73
|
11.70
|
12.93
|
14.61
|
|
Vi exp (l)
|
42.85
|
45.47
|
53.16
|
58.28
|
63.41
|
68.54
|
69.82
|
81.36
|
|
Vi théo (l)
|
35.72
|
43.71
|
49.79
|
53.78
|
63.37
|
67.98
|
73.71
|
81.39
|
|
Vi mod (l)
|
37.21
|
45.64
|
52.25
|
56.27
|
66.42
|
71.29
|
77.37
|
85.51
|
Raie B : Q=0.4l/s
|
T (mn)
|
2.62
|
4.12
|
5.48
|
8.35
|
17.55
|
19.97
|
20.97
|
21.67
|
|
Vi exp (l)
|
21.86
|
24.52
|
45.03
|
52.73
|
78.37
|
82.22
|
88.62
|
98.88
|
|
Vi théo (l)
|
9.57
|
15.78
|
21.63
|
34.44
|
78.32
|
90.36
|
95.38
|
98.91
|
|
Vi mod (l)
|
10.54
|
17.39
|
23.84
|
38.00
|
86.49
|
99.80
|
105.35
|
109.26
|
79
Raie C : Q=0.6l/s
|
T (mn)
|
2.13
|
3.63
|
5.38
|
6.45
|
10.23
|
11.15
|
12.43
|
13.13
|
|
Vi exp (l)
|
18.99
|
38.37
|
51.19
|
61.45
|
89.66
|
98.63
|
103.76
|
130.68
|
|
Vi théo (l)
|
8.83
|
19.18
|
34.28
|
44.88
|
89.51
|
101.89
|
120.03
|
130.38
|
|
Vi mod (l)
|
15.43
|
29.03
|
46.33
|
57.48
|
99.52
|
110.27
|
125.52
|
133.99
|
Raie D : Q=0.8l/s
|
T (mn)
|
1.45
|
2.95
|
4.08
|
5.01
|
9.05
|
10.92
|
11.71
|
13.19
|
|
Vi exp (l)
|
15.75
|
31.34
|
54.42
|
69.81
|
108.27
|
114.68
|
120.57
|
141.60
|
|
Vi théo (l)
|
29.59
|
48.82
|
61.41
|
71.04
|
108.18
|
123.69
|
130.3
|
141.58
|
|
Vi mod (l)
|
18.49
|
35.46
|
47.74
|
57.63
|
99.13
|
117.77
|
125.56
|
140.05
|
Les courbes des volumes infiltrés
expérimentaux, théoriques et modèles des deux arrosages
sont données par les graphes suivants :
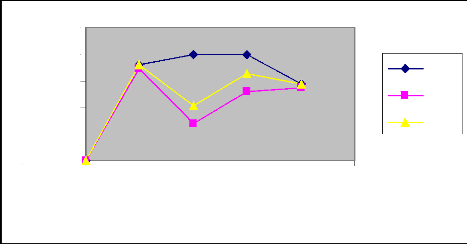
Figure 19 : Courbes des volumes infiltrés
expérimentaux, théoriques et modèles en fonction du temps
(Irrigation N° 1)
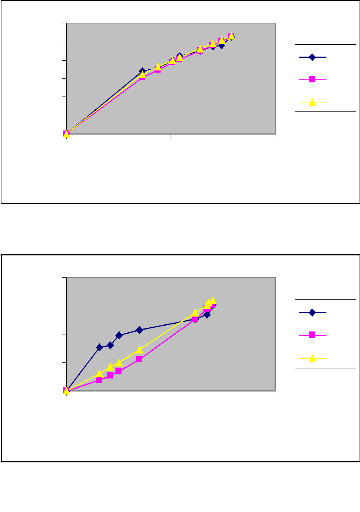
Raie B : Q=0.4l/s
Raie C : Q=0.6l/s
80
120
Volume infiltré (l)
100
80
60
40
20
0
0 5 10 15 20
Temps (mn)
exp
théo
mod
200
Volume infiltré (l)
150
100
50
0
0 10 20 30
Temps (mn)
exp
théo
mod
Raie A : Q=0.2l/s
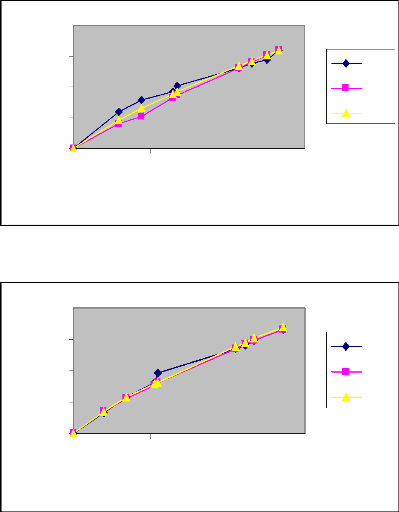
Raie D : Q=0.8l/s
200
Volume infiltré (l)
150
100
50
0
0 5 10 15
Temps (mn)
exp
théo
mod
200
Volume infiltré (l)
150
100
50
0
0 5 10 15
Temps (mn)
exp
théo
mod
81
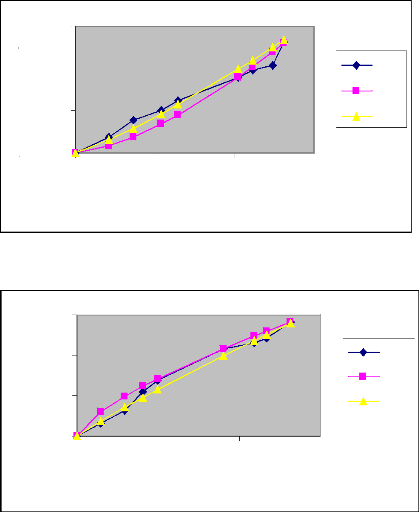
Figure 20 : Courbes des volumes infiltrés
expérimentaux, théoriques et modèles en fonction du temps
(Irrigation N°2)
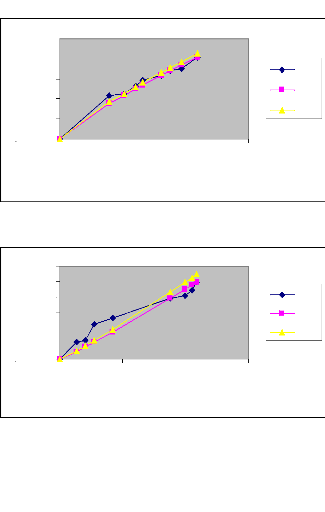
82
Raie A : Q=0.2l/s
Raie B : Q=0.4l/s
Raie C : Q=0.6l/s
100
Volume infiltré (l)
80
60
40
20
0
0 5 10 15 20
Temps (mn)
exp
théo
mod
120
Volume infiltré (l)
100
80
60
40
20
0
0 10 20 30
Temps (mn)
exp
théo
mod
150
Volume infiltré (l)
100
50
0
0 5 10 15
Temps (mn)
exp
théo
mod
Raie D : Q=0.8l/s
150
Volume infiltré (l)
100
50
0
0 5 10 15
Temps (mn)
exp
théo
mod
83
84
Commentaire
Au vu des graphes des figures
précédentes, nous constatons que les courbes modèles aux
débits Q=0.2l/s, Q=0.6l/s, Q=0.8l/s sont plus proches des courbes
expérimentales que des courbes théoriques. Ceci s'explique par le
fait que le calcul du volume infiltré théorique ne prend pas en
considération certains paramètres dont dépend le processus
d'infiltration, tels que la nature du sol, sa texture et sa structure. De
même, nous remarquons que, le volume infiltré pour les trois types
de courbes (expérimentales, théoriques et modèles) demeure
le même dans certains cas comme celui du débit Q=0.2l/s dans la
première irrigation. Nous disons dans ce cas que le processus
d'infiltration obéit fidèlement à la loi de KOSTIAKOV
modifiée.
Par ailleurs, nous constatons dans les deux types
d'irrigation pour le débit Q=0.4l/s, qu'il subsiste toujours un
écart entre les courbes expérimentales et modèles. Les
paramètres de réajustement « K » et « C » ne
pourront pas être affectés à ce type de sol qui a servi de
base à notre essai. Ceci peut s'expliquer par le fait que le sol, au
niveau de cette raie pourrait contenir une couche peu imperméable et
dont la présence a affecté la bonne conduite de
l'expérimentation.
Nous pouvons conclure à l'issue de ces
résultats que la modélisation du processus d'infiltration permet
d'obtenir des résultats plus proches des valeurs expérimentales.
Toutefois, elle serait meilleure si les résultats expérimentaux
étaient plus précis.
Pour voir l'évolution des volumes
infiltrés en fonction des débits, nous allons tracer les graphes
donnant les volumes infiltrés expérimentaux, théoriques et
modèles en fonction des différents débits pour chaque
phase (avancement, durée d'apport et récession).
Volume infiltré (l)
100
40
80
60
20
0
0 0,5 1
Débit (l/s)
exp
théo
mod
85
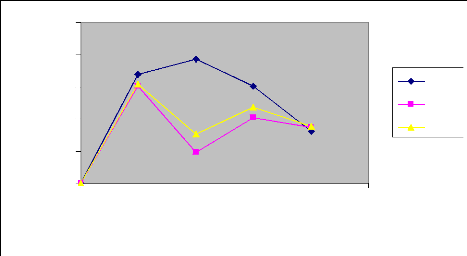
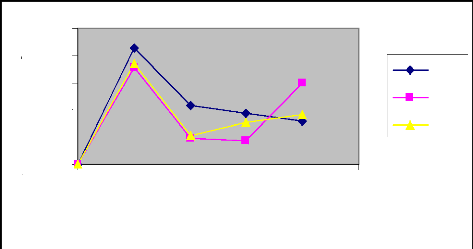
Figure 21 : Volumes infiltrés
expérimentaux, théoriques et modèles en fonction des
débits pour chaque phase (Irrigation
1).
Phase d'avancement
Volume infiltré (l)
100
40
80
60
20
0
0 0,5 1
Débit (l/s)
exp
théo
mod
Phase correspondante à la durée
d'apport
Volume infiltré (l/s)
40
50
30
20
10
0
0 0,5 1
Débit (l/s)
exp
théo
mod
86
Phase de récession
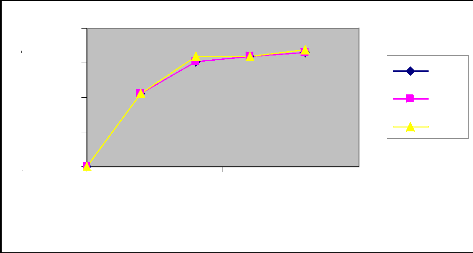
Volume infiltré (l)
200
150
100
50
0
0 0,5 1
Débit (l/s)
exp
théo
mod
Figure 22 : Volumes infiltrés
expérimentaux, théoriques et modèles en fonction des
débits pour chaque phase (Irrigation
2).
Phase d'avancement
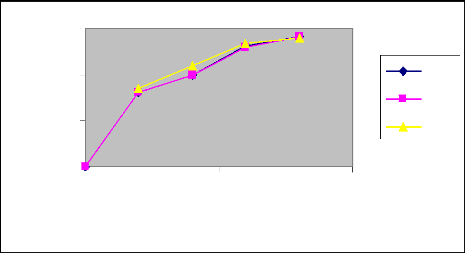
Volume infltré (l)
150
100
50
0
0 0,5 1
Débit (l/s)
exp
théo
mod
87
Phase correspondante à la durée
d'apport
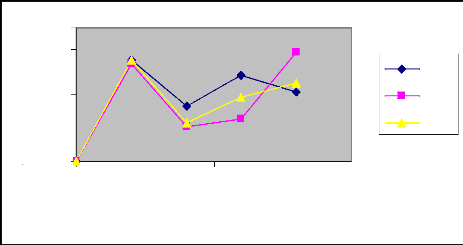
Volume infiltré (l)
40
60
50
30
20
10
0
0 0,5 1
Débit (l/s)
exp
théo
mod
Phase de récession
88
Commentaire
Dans les deux arrosages, nous remarquons au niveau de
la phase d'avancement, que les courbes des volumes infiltrés en fonction
des débits varient presque de la même manière que les
mêmes courbes pendant la phase correspondante à la durée
d'apport. Toutefois, il est à noté au débit Q=0.4l/s, que
la courbe des volumes expérimentaux est bien écarté de
celles deux autres volumes.
A la récession, nous constatons que les trois
courbes ont presque la même allure notamment celles des volumes
infiltrés expérimentaux et modèles.
Au vu de ces résultats, nous disons que la
modélisation est plus précise surtout dans la phase de
récession. Ainsi donc, ces résultats pourront permettre dans le
temps d'optimiser le rendement hydraulique et de minimiser les
pertes.
Par comparaison des graphes des deux arrosages, nous
constatons que les valeurs expérimentales dans l'irrigation N° 2
sont nettement plus précises que celles dans l'irrigation N°1. Cet
état de chose pourrait s'expliquer par le simple fait qu'un sol humide
(pendant l'irrigation N° 2) s'infiltre plus rapidement qu'un sol sec
(pendant l'irrigation N°2).
| 


