3.5. TEST D'HOMOSCEDASTICITE
H0 : Variance constante des erreurs, d'où
l'homoscedasticité (hypothèse nulle).
H1 : Pas de variance constante des erreurs, présence
d'hétérosédasticité (hypothèse alternative).
Seuil de significativité : 0,05 ou 5%
58 | P a g e
Tableau 9 : Test d'HOMOSCEDASTICITE des
variables
|
Intitulés
|
Valeurs
|
|
Chi 2 (1)
|
0,06
|
|
Prob?Chi
|
0,8073
|
|
2
|
|
Source : nous même avec le logiciel
stata
Le test d'homoscedasticité de Breusch-Pagan a
donné une probabilité de 0,8073, largement supérieure au
seuil de significativité de 5 %. Ce résultat nous amène
à accepter l'hypothèse nulle, selon laquelle la variance des
erreurs est constante.
Autrement dit, les erreurs du modèle sont
homoscedastiques, ce qui signifie qu'elles sont réparties de
manière régulière. Ce constat renforce la fiabilité
statistique et la qualité économique des estimations obtenues, en
validant l'un des fondements essentiels des moindres carrés
ordinaires.
3.6. TEST DE NORMALITES GLOBALES DES RESIDUS
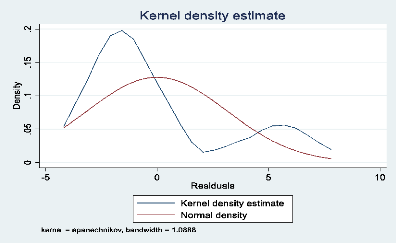
Graphique sur la distribution des résidus
comparée à la norme
59 | P a g e
Le graphique montre que la forme réelle des erreurs du
modèle (ligne bleue) diffère de celle attendue selon une
distribution normale (ligne rouge). Cette irrégularité indique
que les résidus ne suivent pas une distribution parfaitement normale.
Cela remet en question l'usage de tests classiques et renforce l'idée
d'adopter une méthode plus robuste, comme le test de Spearman. Cette
approche est mieux adaptée pour analyser les relations entre variables
lorsque les conditions de normalité ne sont pas remplies.
Tableau 10 : test de normalité globale du
modèle
|
Variable
|
Obs
|
Pr(Skewness)
|
Pr(Kurtosis)
|
Chi 2(2)
|
Prob?Chi2
|
|
Residuals
|
24
|
0.1066
|
0.8010
|
5,53
|
0.0629
|
Source : nous même avec le logiciel
stata
Ce tableau nous montre si les erreurs (appelées
résidus) d'un modèle statistique suivent une distribution
normale, ce qui est souvent une condition importante pour valider les
résultats d'un modèle économique ou scientifique.
Le test révèle que le modèle n'est pas
distribué normalement. L'asymétrie est marquée, et le test
global dépasse le seuil critique de 0,05. Même si le kurtosis
semble conforme, cela ne suffit pas à valider la normalité
globale. En conséquence, on rejette l'hypothèse d'une
distribution gaussienne des résidus. Le modèle demeure
utilisable, mais avec prudence.
Afin d'assurer une analyse valide et rigoureuse, c'est
pourquoi nous avons opté pour une approche non paramétrique,
comme le test de Spearman. Ce test permet d'étudier les relations entre
variables même en cas de non-normalité. Nous avons retenu un seuil
de significativité de 5 % et des hypothèses claires afin de
statuer sur l'existence d'une corrélation fiable.
60 | P a g e
| 


