|
|
École Doctorale IAEM Nancy-Université,
Université Henri Poincaré
|
Mémoire présenté en vue d'obtenir
le diplôme
d'HABILITATION À DIRIGER DES
RECHERCHES
Spécialité : Mathématiques.
CONTROLE DE sysTEMEs MfcANiQuEs ET QuANTiQuEs
pAR DEs
MfTHODEs GfoMfTRiQuEs
Mario SIGALOTTI
Rapporteurs : Pierre ROUCHON
Emmanuel TRÉLAT Enrique ZUAZUA
Soutenue le 5 février 2010 devant le Jury composé
de
Jean-Michel CORON Frédéric JEAN
Jean-Paul GAUTHIER Emmanuel TRÉLAT Marius
TUCSNAK
Man sieht diese Hunde nicht, aber man hört sie.
Mir
machen diese Hunde Angst.
Angst ist vielleicht nicht der richtige
Ausdruck,
sie bringen den Menschen um.
Diese Hunde bringen alles um.
Thomas Bernhard, Frost
Remerciements
Tirer un bilan des activités scientifiques qui m'ont
occupé après ma thèse signifie en premier lieu remercier
un certain nombre de personnes qui m'ont grandement aidé pendant ces
dernières années.
D'abord, je tiens à remercier Marius Tucsnak pour
m'avoir si chaleureusement accueilli au sein de son équipe, pour ses
encouragement et son soutien dans la prise de responsabilités et pour
avoir été une source continue de conseils et intuitions
mathématiques. Je lui suis reconnaissant aussi pour avoir toujours su
rendre paisibles ces années de travail à Nancy par son naturel
contagieusement joyaux. C'est sans oublier la gratitude que je lui dois pour
avoir accepté de faire partie de mon jury.
Un très grand merci va à mes amis-collaborateurs
Ugo Boscain et Yacine Chitour, sans lesquels je n'aurais probablement pas su me
résoudre à m'engager dans le parcours exigeant de la recherche :
je voudrais toutefois les décharger formellement de toute
responsabilité quant au résultat de leur soutien amical...
Je voudrais remercier Pierre Rouchon et Emmanuel Trélat
pour m'avoir honoré d'être rapporteurs de cette thèse
d'habilitation et pour avoir accepté de faire partie de ce jury. Enrique
Zuazua a aussi accepté d'être rapporteur et je lui en suis
vivement reconnaissant.
Je voudrais exprimer toute ma gratitude à Jean-Michel
Coron, Frédéric Jean et Jean-Paul Gauthier pour avoir
accepté de faire partie de ce jury. Leur présence m'honore et est
un grand plaisir.
Je remercie chaleureusement Andrei Agrachev, à qui je
dois scientifiquement tellement du peu que j'ai pu atteindre, pour avoir
accepté de faire partie de ce jury, avant qu'un empêchement nous
prive du plaisir de sa présence ici aujourd'hui.
Les résultats présentés dans les pages
qui suivent, ainsi que ceux qui ont occupé les mois qui se sont
écoulés depuis le commencement de la rédaction de cette
thèse d'habilitation, sont le fruit de la collaboration avec des
nombreux amis et collègues que je tiens à remercier vivement :
merci à María Barbero-Liñán, Grégoire
Charlot, Thomas Chambrion, Jamal Daafouz, Roberta Ghezzi, Paolo Mason, Yannick
Privat, Ulysse Serres, François Alouges, Karine Beauchard, Alexandre
Bombrun, Antoine Chaillet, Martin Gugat, Fouad El Hachemi, Falk Hante, Antonio
Loría, Jean-Baptiste Pomet, Pierre Riedinger, Dominique Sugny et
Jean-Claude Vivalda.
Je voudrais aussi exprimer ma gratitude aux coéquipiers
de MIAOU, APICS et CORIDA et en particulier à Bilal Atfeh, Juliette
Leblond, Karim Ramdani et Takéo Takahashi, pour leur écoute et
soutien, avec une mention particulière pour Bilal et Takéo, qui
m'ont eu comme copain de bureau et qui ont su stoïquement endurer mon
désordre débordant.
Pour terminer, je ne peux pas manquer de remercier ceux qui,
de manière directe ou indirecte, ont rendu possibles les travaux
présentés ici : ma famille chérie, bien sûr, ainsi
que les amis de Nancy, Nice, Udine ou ailleurs, et en particulier Natasha,
Marco, Ilaria, Francesca, Laura, Maurizio, Assia, Marius, Guillaume, Camille et
Justine. Merci.
Table des matières
|
1
2
|
Travaux de recherche 8
Introduction 11
Commandabilité et commande des systèmes non
linéaires de dimension finie 15
1.1 Problème de
Dubins sur des surfaces à courbure négative [MS.10] 15
1.2 Suivi de trajectoire pour un sous-marin dont le mouvement est
régi par les lois
de Kirchhoff [MS.7] 17
1.3 Propriétés de commandabilité d'une
classe de systèmes modélisant la nage de
micro-organismes [MS.3] 19
Contrôle quantique et propriétés
génériques de l'équation de Schrödinger
23
|
|
2.1
|
Commandabilité de l'équation de Schrödinger
bilinéaire à spectre discret [MS.5] .
|
23
|
|
2.2
|
Commandabilité de la rotation d'une molécule
quantique [MS.20]
|
26
|
|
2.3
|
Généricité des propriétés des
fonctions et valeurs propres de l'équation de Laplace-
|
|
|
|
Dirichlet [MS.4]
|
27
|
|
2.4
|
Généricité par rapport aux potentiels de la
commandabilité de l'équation de Schrö-
|
|
|
|
dinger bilinéaire à spectre discret [MS.1]
|
29
|
|
3
|
Stabilité et stabilisation des systèmes
hybrides
|
33
|
|
3.1
|
Stabilité des systèmes à commutations non
linéaires sur le plan [MS.9]
|
33
|
|
3.2
|
Systèmes soumis à une condition d'excitation
persistante [MS.6,23]
|
35
|
|
3.3
|
Analyse de stabilité des systèmes linéaires
à commutations à temps discret par le
|
|
|
|
biais de fonctions de Liapounov quadratiques [MS.27]
|
37
|
|
4
|
Géométrie presque riemannienne
[MS.2,8,15]
|
39
|
|
Perspectives de recherche
|
47
|
Travaux de recherche
Résumé
|
Type de publication
|
#
|
|
Revues internationales
|
14
|
|
Revues nationales
|
4
|
|
Conférences internationales
|
16
|
|
Rapports de recherche soumis à publication
|
4
|
Articles parus dans des revues internationales avec
comité de lecture
[MS.1] P. MASON ET M. S., Generic controllability properties
for the bilinear Schrödinger equation, Communications in Partial
Differential Equations, à paraître.
[MS.2] A. A. AGRAcHEV, U. BOScAIN, G. CHARLOT, R. GHEZZI ET M.
S., Two-dimensional almost-Riemannian structures with tangency points,
Annales de l'Institut Henri Poincaré (C) Analyse Non Linéaire,
à paraître.
[MS.3] M. S. ET J.-C. VIVALDA, Controllability properties
of a class of systems modeling swimming microscopic organisms, ESAIM :
Control, Optimisation and Calculus of Variations, à paraître.
[MS.4] Y. PRIVAT ET M. S., The squares of the
Laplacian-Dirichlet eigenfunctions are generically linearly independent,
ESAIM : Control, Optimisation and Calculus of Variations, à
paraître.
[MS.5] T. CHAMBRION, P. MASON, M. S. ET U. BOScAIN,
Controllability of the discrete-spectrum Schrödinger equation driven
by an external field, Annales de l'Institut Henri Poincaré (C)
Analyse Non Linéaire, 26 (2009), pages 329-349.
[MS.6] A. CHAILLET, Y. CHITOUR, A. LORIA ET M. S., Uniform
stabilization for linear systems with persistency of excitation. The neutrally
stable and the double integrator cases, Mathematics of Control, Signals,
and Systems, 20 (2008), pages 135-156.
[MS.7] T. CHAMBRION ET M. S., Tracking control for an
ellipsoidal submarine driven by Kir-
chhoff's laws, IEEE
Transactions on Automatic Control, 53 (2008), pages 339349.
[MS.8] A. A. AGRAcHEV, U. BOScAIN ET M. S., A
Gauss-Bonnet-like formula on two-dimensional almost-Riemannian manifolds,
Discrete and Continuous Dynamical Systems Series A, 20 (2008), pages 801822.
[MS.9] U. BOScAIN, G. CHARLOT ET M. S., Stability of planar
nonlinear switched systems, Discrete and Continuous Dynamical Systems
Series A, 15 (2006), pages 415432.
[MS.10] M. S. ET Y. CHITOUR, Dubins' problem on surfaces II :
Nonpositive curvature, SIAM Journal on Control and Optimization, 45
(2006), pages 457482.
[MS.11] Y. CHITOUR ET M. S., Dubins' problem on surfaces. I.
Non-negative curvature, Journal of Geometrical Analysis, 15 (2005), pages
565587.
[MS.12] M. S., Local regularity of optimal trajectories for
control problems with general boundary conditions, Journal of Dynamical
and Control Systems, 11 (2005), pages 91-123.
[MS.13] A. A. AGRAcHEV ET M. S., On the local structure of
control functions corresponding to time-optimal trajectories in
R3, SIAM Journal on Control and Optimization, 42 (2003), pages
513-531.
[MS.14] G. ALESSANDRINI ET M. S., Geometric properties of
solutions to the anisotropic p-Laplace equation in
dimension two, Annales Academiæ Scientiarum Fennicæ.
Mathematica, 21 (2001), pages 249-266.
Articles parus dans des revues nationales
[MS.15] U. BOScAIN ET M. S., High-order angles in
almost-Riemannian geometry, Actes de Séminaire de Théorie
Spectrale et Géométrie, 25 (2008), pages 41-54.
[MS.16] A.A. AGRAcHEV, U. BOScAIN ET M. S., Two-dimensional
almost-Riemannian manifolds, Lecture notes of Seminario Interdisciplinare
di Matematica, 6 (2007), pages 17-31.
[MS.17] M. S., Regularity properties of optimal trajectories
of single-input control systems in dimension three, Journal of
Mathematical Sciences, 126 (2005), pages 1561-1573.
[MS.18] A. BRAIDES, M. S. GELLI ET M. S., The passage from
non-convex discrete systems to variational problems in Sobolev spaces : the
one-dimensional case, Proceedings of the Steklov Institute of Mathematics,
236 (2002), pages 395-414.
Articles pour des conférences internationales avec
comité de lecture
[MS.19] F. ALOuGES, K. BEAucHARD ET M. S., Magnetization
switching in small ferromagnetic ellipsoidal samples, Proceedings of the
48th IEEE Conference on Decision and Control, Shanghai, Chine, 2009.
[MS.20] U. V. BOScAIN, T. CHAMBRION, P. MASON, M. S. ET D.
SuGNY, Controllability of the rotation of a quantum planar molecule,
Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai,
Chine, 2009.
[MS.21] T. CHAMBRION ET M. S., Simultaneous approximate
tracking of density matrices for a system of Schrödinger equations,
Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai,
Chine, 2009.
[MS.22] M. S., P. MASON, U. V. BOScAIN ET T. CHAMBRION,
Generic controllability properties for the bilinear Schrödinger
equation, Proceedings of the 48th IEEE Conference on Decision and Control,
Shanghai, Chine, 2009.
[MS.23] Y. CHITOuR ET M. S., On the stabilization of
permanently excited linear systems, Proceedings of the 48th IEEE
Conference on Decision and Control, Shanghai, Chine, 2009.
[MS.24] A. A. AGRAcHEV, U. V. BOScAIN, G. CHARLOT, R. GHEZZI
ET M. S., Two-dimensional almost-Riemannian structures with tangency
points, Proceedings of the 48th IEEE Conference on Decision and Control,
Shanghai, Chine, 2009.
[MS.25] P. RIEDINGER, M. S. ET J. DAAFOuZ, On the
observability of the flying capacitor converter, Proceedings of the 10th
European Control Conference, Budapest, Hongrie, 2009.
[MS.26] T. CHAMBRION, P. MASON, M. S. ET U. V. BOScAIN,
Controllability properties of discrete-spectrum Schrödinger
equations, Proceedings of the 47th IEEE Conference on Decision and
Control, Cancun, Mexique, 2008.
[MS.27] P. MasoN, M. S. ET J. Daafouz, On stability
analysis of linear discrete-time switched systems using quadratic Lyapunov
functions, Proceedings of the 46th IEEE Conference on Decision and
Control, Nouvelle Orléans, USA, 2007, pages. 5629-5633.
[MS.28] A. ChaillET, Y. ChiTour, A. Loria ET M. S.,
Towards uniform linear time-invariant stabilization of systems with
persistency of excitation, Proceedings of the 46th IEEE Conference on
Decision and Control, Nouvelle Orléans, USA, 2007, pages 6394-6399.
[MS.29] M. GugaT, M. S. ET M. TucsNak, Robustness analysis
for the boundary control of the string equation, Proceedings of the 9th
European Control Conference, Kos, Grèce, 2007.
[MS.30] T. ChambrioN ET M. S., Controllability and output
tracking for an ellipsoidal submarine driven by Kirchhoff's laws, 32nd
Annual Conference of the IEEE Industrial Electronics Society (IECON-2006),
pages 567-572.
[MS.31] Y. ChiTour ET M. S., Controllability of the Dubins
Problem on Surfaces, Proceedings of the 44th IEEE Conference on Decision
and Control, Séville, Espagne, 2005, pages 1439- 1444.
[MS.32] U. V. BoscaiN, G. CharloT ET M. S., Stability of
Nonlinear Switched Systems on the Plane, Proceedings of the 44rd IEEE
Conference on Decision and Control, Séville, Espagne, 2005, pages
3285-3290.
[MS.33] A. BombruN, J.-B. PomET ET M. S., Mechanical
Systems and Rendez-Vous Controllability, Proceedings of the 44rd IEEE
Conference on Decision and Control, Séville, Espagne, 2005, pages
8271-8275.
[MS.34] Y. ChiTour ET M. S., On the controllability of the
Dubins' problem for surfaces, in Proceedings of SSSC04 - Second IFAC
Symposium on System, Structure and Control, Oaxaca, Mexique, 2004, pages
614-616.
Rapports de recherche soumis à
publication
[MS.35] Y. ChiTour ET M. S., On the stabilization of
persistently excited linear systems.
[MS.36] P. RiEdiNgEr, M. S. ET J. Daafouz, On the
characterization of invariant sets of switched linear systems.
[MS.37] M. GugaT ET M. S., Star-shaped string networks :
Switching boundary feedback stabilization.
[MS.38] M. BarbEro-LiñáN ET M. S., High order
sufficient conditions for tracking.
Introduction
L'activité de recherche à laquelle je me suis
dédié depuis mon doctorat peut être organisée autour
de quatre axes principaux. Chaque chapitre de ce mémoire correspond
à l'un de ces quatre axes.
Le premier est celui qui se rattache le plus directement
à ma thèse de doctorat. Il s'agit de la commandabilité et
de la planification de trajectoires des systèmes non linéaires de
dimension finie. Des premiers résultats dans ce domaine ont en effet
été présentés dans mon mémoire de
thèse et portaient sur la commandabilité de systèmes de
type Dubins sur les surfaces à courbure positive à
l'extérieur d'un domaine borné. La suite logique de ce travail a
été d'étudier les propriétés de
commandabilité de ces mêmes systèmes de type Dubins dans le
cas où la courbure est négative. Rappelons que le modèle
de Dubins décrit le mouvement d'un véhicule dont la valeur
absolue de la vitesse linéaire est constante et
l'accélération angulaire est uniformément bornée.
En collaboration avec Y. Chitour, sur impulsion d'une observation faite par P.
Pansu, nous avons caractérisé les surfaces à courbure
négative pour lesquelles ce système est commandable
indépendamment de la borne sur l'accélération angulaire et
nous avons étudié la structure des trajectoires minimisant le
temps. Dans un deuxième travail, en collaboration avec T. Chambrion,
nous avons étudié la commandabilité et la commande d'un
autre type de véhicule, un sousmarin dont le mouvement en l'absence de
contrôles est décrit par les lois de Kirchhoff. Sous des
hypothèses de symétrie du véhicule et en l'absence
d'obstacles, nous avons pu fournir un algorithme permettant de
déterminer - pour des actionneurs très naturels dans ce contexte
- des lois de commande permettant de suivre de façon approchée
une trajectoire quelconque. Enfin, d'autres résultats concernant la
locomotion dans un fluide ont été obtenus en collaboration avec
J.-C. Vivalda. Il s'agissait dans ce cas d'étudier le mouvement d'un
micro-organisme qui s'autopropulse grâce aux cilia
présents sur sa surface, dont la modélisation a
été proposée dans [101]. Si dans le cas du sous-marin
c'est la possibilité de considérer la viscosité nulle qui
permet de travailler avec un système réduit de dimension finie,
pour les micro-organismes cela est au contraire la conséquence de la
grande viscosité due à leur petite taille. Les deux
systèmes de contrôle ainsi obtenus sont bien sûr très
différent, mais tous les deux sont non linéaires,
sousactionnés et dotés d'une structure lagrangienne naturelle.
Le deuxième axe est fortement lié au premier,
naissant comme prolongation aux systèmes de dimension infinie des
mêmes problématiques de commandabilité et commande. En
collaboration avec U. Boscain, T. Chambrion et P. Mason je me suis
intéressé aux propriétés de
contrôlabilité de l'équation de Schrödinger
bilinéaire. L'approche choisie, inspirée par l'importante
littérature sur la commande de systèmes invariants sur des
groupes de Lie compacts et en particulier par le travail [3] d'Agrachev et
Chambrion, a été d'étendre à l'équation de
Schrödinger des propriétés de contrôlabilité de
ses approximations de Galerkin. (Ce procédé avait
été déjà appliqué aux équations de
NavierStokes dans [7, 99].) La réussite de l'approche est basée
sur un résultat de suivi de trajectoire pour des approximations de
Galerkin. Des points forts du résultat obtenu sont qu'il s'applique
aussi aux matrices de densité (commande simultanée de
systèmes identiques avec différentes conditions initiales), aux
domaines non bornés avec opérateurs non bornés (pourvu
que le spectre soit discret) et aux variétés
différentielles. Ce dernier point est important pour les applications,
permettant ainsi d'étudier des problèmes de commande de
l'orientation d'une molécule (travail en collaboration avec U. Boscain,
T. Chambrion, P. Mason et D. Sugny). Même si le résultat
général que nous avons obtenu porte sur la commandabilité
du système, vue comme propriété d'existence, il est
basé sur une approche constructive et nous espérons pouvoir en
tirer des algorithmes explicites de commande. Mis a part l'hypothèse que
le spectre de l'opérateur non contrôlé soit discret, les
conditions suffisantes que nous avons proposées et qui garantissent la
commandabilité approchée de l'équation de Schrödinger
sont données par une infinité dénombrable de conditions de
non annulation. Cela nous a poussé a en étudier la
généricité par rapport aux différents
paramètres caractérisant l'équation de Schrödinger
contrôlée : son domaine de définition, le potentiel non
contrôlé et le potentiel de contrôle. La première de
ces trois dépendances amène très naturellement a se poser
les deux questions suivantes : les carrés des fonctions propres de
l'opérateur de Laplace-Dirichlet sont-ils linéairement
indépendants, génériquement par rapport au domaine? Une
combinaison linéaire finie a coefficients non nuls et fixés
arbitrairement des valeurs propres de l'opérateur de Laplace-Dirichlet
est-elle différente de zéro, génériquement par
rapport au domaine? Ces mêmes questions surgissent aussi dans d'autres
domaines des mathématiques appliqués (cf. [64, 116]). En
collaboration avec Y. Privat, nous avons développé un
schéma général de preuve qui donne une réponse
positive a ces deux questions. Ce schéma, inspiré par un travail
de Hillairet et Judge ([66]), est basé sur des résultats de
perturbation analytique ([69, 98, 113]) qui permettent de contourner les
difficultés liées aux dérivées par rapport a des
déformations locales du domaine (cf., par exemple, [45, 75, 89, 90]).
J'ai utilisé ce même principe de déformations analytiques a
longue distance, cette fois en collaboration avec P. Mason, pour
démontrer la généricité de la commandabilité
approchée de l'équation de Schrödinger
séparément par rapport aux deux potentiels, celui de
contrôle et celui non contrôlé.
Le troisième axe de recherche présenté
dans ce document concerne la stabilité et la stabilisation des
systèmes hybrides. Le premier problème auquel je me suis
intéressé a été celui de la stabilité
uniforme des systèmes a commutations. En collaboration avec U. Boscain
et G. Char-lot, nous avons étudié le cas des systèmes a
commutations définis sur R2 par deux champs de vecteurs non
linéaires ayant chacun l'origine comme équilibre globalement
asymptotiquement stable. Nous avons obtenu des conditions topologiques sur
l'ensemble où les deux champs de vecteurs sont parallèles
garantissant a la fois la stabilité asymptotique uniforme a l'origine,
la stabilité, ou l'instabilité du système commuté.
L'intérêt de ces conditions est de pouvoir être directement
testées sur les champs de vecteurs, sans avoir besoin d'en calculer les
flots, ni de chercher des fonctions de Liapounov communes. D'autres
résultats, en collaboration avec J. Daafouz et P. Mason ont
été obtenus sur les critères de stabilité des
systèmes a commutations linéaires a temps discret. En
particulier, nous avons pu démontrer l'équivalence de l'existence
d'une fonction de Liapounov dans différentes classes de fonctions
quadratiques. Ce résultat permet de ramener la recherche a une classe de
fonctions pour laquelle des tests d'existence viables existent. En
collaboration avec A. Chaillet, Y. Chitour et A. Loría, nous avons aussi
étudié la stabilisation d'une classe de systèmes a
commutations commandés. Nous avons considéré le cas d'un
système de contrôle linéaire dont la partie
commandée de la dynamique est activée seulement sur certains
intervalles de temps par une loi de commutation qui satisfait une condition
d'excitation persistante. Nous nous sommes intéressé a la
question de l'existence d'un retour d'état linéaire qui stabilise
le système a l'origine uniformément par rapport a la loi de
commutation. Dans le cas où un tel retour d'état existe, nous
avons étudié le taux maximal de convergence vers l'origine que
l'on peut atteindre.
Enfin, le quatrième et dernier axe de recherche
présenté dans ce mémoire concerne une catégorie
particulière de structures sous-riemanniennes a rang non constant. En
collaboration avec A. Agrachev, U. Boscain, G. Charlot et R. Ghezzi, nous avons
introduit la notion de structure
presque riemannienne pour indiquer une structure
sous-riemannienne à rang non constant engendrée localement par un
nombre de champs de vecteurs égal à la dimension de la
variété. Sous des conditions de généricité,
cette structure définit, sur le complémentaire d'un ensemble de
codimension un (dit ensemble singulier), une structure riemannienne. En
particulier, dans le cas des variétés compactes sans bord de
dimension deux, nous avons introduit une notion d'intégrale de la
courbure gaussienne sur le complémentaire de l'ensemble singulier et
nous avons ainsi démontré une version
généralisée de la formule de Gauss-Bonnet. Cette
même formule admet aussi une généralisation au cas des
surfaces avec bord, sous des contraintes d'admissibilité des
intersections avec le bord de l'ensemble singulier.
Chapitre 1
Commandabilité et commande des
systèmes non linéaires de dimension
finie
1.1 Problème de Dubins sur des surfaces à
courbure négative [MS.10]
Soit (M, m) une variété
riemannienne connexe, orientable et complète. Indiquons par N
= UM son fibré tangent unitaire. Les points de
N sont les couples (p, v), oil p ?
M, v ? TpM et
m(v, v) = 1. Pour tout å >
0 nous pouvons considérer le problème de Dubins qui
consiste à trouver, pour tous
(p1,v1),
(p2,v2) ? N, une
courbe ã [0,T] ? M
paramétrée par son abscisse curviligne dont la courbure
géodésique est bornée par å, telle
que ã(0) = p1,
ÿã(0) = v1,
ã(T) = p2,
ÿã(T) = v2 et
minimisant T. Dans la suite nous nous restreignons au cas oil
M est de dimension deux. Le problème de Dubins
s'écrit alors comme le problème de temps minimum :
(Då) qÿ =
f(q) +
ug(q), q ? N, u ?
[-å,å],
oil f est le générateur
infinitésimal du flot géodésique sur N et
g est le champ de vecteurs engendrant la rotation sur les
fibres de N de vitesse angulaire constante égale
à 1. Les contrôles admissibles sont toutes les fonctions
mesurables u à valeurs dans l'intervalle
[-å, å].
En 1957 Dubins ([54]) détermina la structure globale
des trajectoires optimales de (Då) sur R2
muni de la structure euclidienne : ce trajectoires optimales sont la
concaténation d'au plus trois arcs de cercle de rayon 1/å
ou de segments. Des conditions nécessaires
supplémentaires sur les longueurs des arcs d'une concaténation
optimale ont été obtenues par Sussmann et Tang ([109]). Des
problèmes de type Dubins ont été étudiés
pour les surfaces simplement connexes à courbure constante ([44, 68,
84]), également en dimension supérieure à deux ([85, 86,
110]).
Une motivation du travail de recherche présenté
ici (et de l'article précédent [MS.11]) vient de la remarque que,
en généralisant le problème de Dubins du cas euclidien
à une surface riemannienne quelconque, la commandabilité de
(Då) devient une propriété
difficile à établir.
Nous sommes poussés à considérer une
propriété intrinsèque de M invariante par
changement d'échelle : savoir si (Då)
est commandable pour tout å > 0. Cette
propriété a une interprétation géométrique
évidente si l'on remarque que la projection sur M des
trajectoires de (Då) donne l'ensemble des
courbes C1 sur M dont la courbure
géodésique est bornée par å. Nous
pouvons donc reformuler la propriété mentionnée ci-dessus
en disant que (M, m) est uniformément connectable
par arcs si, pour tous (q1, v1),
(q2, v2) ? N et
pour tout å > 0, il existe une courbe
ã : [0, T] - M
de courbure géodésique inférieure à
å joignant q1 à
q2 et telle que ã'(0) =
v1, ã'(T)
= v2.
Un premier résultat, que nous obtenons par des arguments
de stabilité au sens de Poisson, est le suivant.
Proposition 1.1 Soit M
une surface riemannienne complète et connexe. Alors
M est uniformément connectable par arcs si au
moins l'une des deux propriétés suivantes est
vérifiée : (a) l'aire de M
est finie, (b) le flot
géodésique sur M est topologiquement
transitif.
Le rôle de la courbure gaussienne K :
M - R de (M, m) dans l'étude de la
connectabilité uniforme par arcs de M est
suggéré par la structure de l'algebre de Lie engendrée par
f et g. En effet,
[f,
[f,g]](q) =
--K(ð(q))g(q)
pour tout q E N, oil ð :
N - M est fa fibration canonique (cf., par exemple, [106]).
Dans [MS.11] nous avons étudié, en collaboration
avec Y. Chitour, le cas oil la courbure sur M est positive.
Dans la suite nous considérons le cas oil la courbure gaussienne de
M est négative. On sait alors que M
peut être identifiée avec un espace quotient
X/, oil X est une surface d'Hadamard
(c'est-à-dire, une variété de dimension deux simplement
connexe à courbure négative) et est un groupe
d'isométries de M préservant l'orientation qui
agit librement et de façon discontinue sur X.
Nous pouvons démontrer le résultat suivant.
Théorème 1.2 Soit
M une surface riemannienne complète, connexe
et dont la courbure gaus-
sienne K est
négative. Soit X le revêtement universel
de M. Alors M est
uniformément connec-
table par arcs si au moins l'une des deux
propriétés suivantes est satisfaite : (i) M
est du premier
f
type ; (ii) pour tout r > 0 et
tout secteur S de X,
supp?S BX(p,r) KdA =
0.
Rappelons que M est du premier type si
l'ensemble limite de est égal au bord idéal de X
(cf. [16]). La notation BX(p, r)
indique l'ensemble des points de X qui ont distance
riemannienne inférieure à r de
p.
Nous pouvons transformer les conditions suffisantes pour que
M soit uniformément connectable par arcs du
théorème 1.2 en conditions nécessaires et suffisantes en
introduisant des restrictions sur le comportement de K.
Théorème 1.3 Soit
M une surface riemannienne complète, connexe
dont la courbure gaussienne K est majorée par
une constante strictement négative. Alors M
est uniformément connectable par arcs si et seulement si
M est du premier type.
Théorème 1.4 Soit
M une surface riemannienne complète, connexe
dont la courbure gaus-
sienne K est
négative et minorée. Supposons que M
est du deuxième type est notons X
son
revêtement universel. Alors M
est uniformément connectable par arcs si et seulement si
pour
f
tout r > 0 et tout secteur
S de X, supp?S
BX(p,r) KdA = 0.
Dans le cas oil K change de signe nous pouvons
démontrer le résultat suivant. Proposition 1.5
Soit M une surface riemannienne dont le
groupe fondamental est de type fini. Soit K
bornée et négative à l'extérieur d'un
sous-ensemble compact de M. Supposons que
tout
demi-cylindre riemannien de M est
strict. Alors M est uniformément connectable
par arcs si et
f
seulement si, pour tout demi-plan H
contenu dans M et pour tout
r > 0, supp?H BM
(p,r) KdA =
f
?U BM (p,r) KdA <
0.
0. En particulier, (i) M est
uniformément connectable par arcs si
fM KdA > --oc; (ii)
M n'est pas uniformément connectable par arcs
s'il existe r > 0 et un demi-cylindre riemannien
U C M tels que
supp
Rappelons qu'un sous-ensemble U de M
est dit un demi-cylindre riemannien s'il est
difféomorphe à S1 ×
[0, 8) et qu'il est dit strict si
K8(U) = - j U KdA -
k(?U) =6 0, oh
k(?U) est l'intégrale de la courbure
gaussienne de ?U. Le théorème de Cohn-Vossen
garantit alors que K8(U)
> 0 (cf. [104]).
Nous terminons cette section par un résultat sur la
structure des trajectoires optimales du problème de Dubins. Ce
résultat peut être obtenu comme une conséquence du Principe
du Maximum de Pontriaguine (cf., par exemple, [6]).
Proposition 1.6 Tout arc singulier d'une
trajectoire temps-optimale de (Då)
est le relèvement d'un segment géodésique
(indépendamment du signe de K). Si
K est majorée par une constante strictement
négative et å est suffisamment petit,
alors toute trajectoire temps-optimale de
(Då) est la concaténation
d'un arc bang, un arc singulier et un arc bang (chaque arc ayant
éventuellement longueur nulle).
1.2 Suivi de trajectoire pour un sous-marin dont le
mouvement est régi par les lois de Kirchhoff [MS.7]
Dans cette section nous étudions la commande d'un
véhicule ellipsoïdal immergé dans un volume infini de fluide
idéal. Le modèle choisi est adapté à la description
du mouvement des véhicules sous-marins sans pilote.
Nous supposons dans la suite que le véhicule a la
même densité moyenne que le fluide (de telle sorte que sa
dynamique n'est pas affectée par la gravité) et que son centre de
masse coïncide avec le centre de l'ellipsoïde. Nous supposons aussi
que le fluide est non visqueux, incompressible, irrotationnel et qu'il remplit
R3. Sous ces hypothèses, le mouvement du véhicule est
décrit par les lois de Kirchhoff (cf. [70]). En raison de la nature
potentielle du fluide l'état du système est
déterminé par un nombre fini de paramètres.
Notons par r ? R3 la position du
centre de masse du véhicule et par A ? SO(3) son
orientation, calculées par rapport à un système de
coordonnées galiléen. Notons aussi par v et
ù ses vitesses linéaire et angulaire,
calculées par rapport à un système de coordonnées
attaché au véhicule. Nous avons
Aÿ =
AS(ù), rÿ =
Av, (1.1)
oh S : R3 ? so(3)
est la bijection linéaire qui associe à un vecteur x ?
R3 la matrice 3 × 3
antisymétrique S(x) telle que
x ? y = S(x)y
pour tout y dans R3.
Associons à (ù, v) les
impulsions correspondants (II, P) définis
par
! !
II ù
= M , (1.2)
P v
oh la matrice
)
Je + Jf
03×3
M = 03×3
Me + Mf
est composée des blocs 3 × 3
suivants : Je est la matrice d'inertie de
l'ellipsoïde; Me est la matrice
identité 3 × 3, dénotée par Id3 dans
la suite, multipliée par la masse du véhicule; Jf
et Mf prennent en compte l'action du fluide sur le
solide. La forme ellipsoïdale du véhicule implique que Jf
et Mf sont diagonales par rapport au repère
donné par les axes de l'ellipsoïde. Les coefficients de Jf
et Mf sont obtenus à partir des solutions de
certaines problèmes aux limites associés à
l'équation de Laplace et ne dépendent pas de la distribution de
masse à l'intérieur du solide.
La dynamique suivie par (Ð, P) est
donnée par les équations de Kirchhoff :
{ Ðÿ = Ð ? ù
+ P ? v + T,
(1.3)
Pÿ = P ? ù
+ F,
oil T et F sont respectivement
le couple et la force extérieurs appliqués au solide.
Une dernière hypothèse simplificatrice est que
les axes d'inertie du véhicule coïncident avec les axes de
l'ellipsoïde. Cela est vrai, par exemple, si la distribution de masse du
sous-marin est symétrique par rapport à au moins deux des plans
engendrés par les axes de l'ellipsoïde.
Sous les conditions présentées ci-dessus, la
matrice M peut être supposée diagonale. Notons
par M1, M2, M3 et
J1, J2, J3 les entrées
diagonales de Me + Mf et
Je + Jf respectivement.
Supposons que le sous-marin soit commandé par une
accélération le long de l'un des axes de l'ellipsoïde et par
deux accélérations angulaires autour des deux autres
axes. T et F s'écrivent alors
|
?
?
T=?
|
u1 0
u2 ) , F =
(0 ) , u1, u2,
u3 ? R.
0 u3
|
Le système ainsi obtenu a déjà
été considéré du point de vue du contrôle par
nombreux auteurs : signalons [13, 30, 31, 72, 88] pour la commande des
équations de Kirchhoff et [40, 47, 46] pour le modèle complet
(états-impulsions).
Nous pouvons démontrer le résultat suivant.
Théorème 1.7
Soit J1 =6 J2 ou
M1 =6 M2. Alors, le système de
contrôle (1.1)-(1.3) est complètement commandable en temps
arbitrairement petit. De plus, pour toute trajectoire lisse
(A, r) : [0,
T] ? SO(3)×R3,
pour toutes conditions initiales Ð0, P0
? R3 et pour toute tolérance o
> 0, il existe une loi de commande mesurable et
bornée u =
(u1,u2,u3) : [0,
T] ? R3 telle que la
trajectoire t 7?
(A(t),r(t),Ð(t),P(t))
de (1.1)-(1.3) correspondant à u et avec
condition initiale
(A(0),r(0),Ð(0),P(0))
= ( A(0),
r(0),Ð0, P0)
vérifie ||
A(t) -
A(t)|| +
||r(t) -
r(t)|| < o pour
tout t ? [0, T].
La démonstration du théorème est
basée sur une approche de type backstepping : on utilise les
coordonnés Ð1, Ð2 et P3, qui sont
contrôlées directement par u1,
u2 et u3, comme nouvelles commandes dans les
équations de Ð3, P1 et P2. Nous
commandons ces dernières suffisamment bien (c'est-à-dire au sens
intégral, comme énoncé dans le lemme 1.8) pour pouvoir les
utiliser à leur tour comme commandes dans les équations
de r et A. Le point clé de la
démonstration est donc le suivant.
Lemme 1.8 Soit J1
=6 J2 ou M1 =6
M2. Fixons T > 0 et une courbe
lisse (Ð, P ) :
[0, T] ? R6.
Il existe alors une suite un
dans L°°([0,
T], R3) telle que la suite
(Ðn, Pn) de
solutions de (1.3) correspondant à
un et ayant
(Ðn(0), Pn(0)) =
(Ð(0), P (0)) comme
condition initiale satisfait
(Ðn1(T),
Ðn2 (T),
P1n
(T),
P2n
(T),
P3n
(T)) ?
(Ð1(T),
Ð2(T), P1(T),
P2(T),
P3(T)),
Ðn3(t)
? Ð3(t),
fot t
(Ð7ii
(ô)
,Ð72'
(ô) , Pli
(ô) , II
(ô) , PT'
(ô))d --> r f
(Ð1(ô)
,Ð2(ô) ,
P1(ô) , P2
(ô), P3
(ô))dô
0
pour n ? 8, oil les deux
dernières convergences sont uniformes par rapport à
t ? [0, T].
La méthode de démonstration fournit un algorithme
pour sélectionner une famille de lois de commande oscillantes qui
donnent lieu au suivi de trajectoire souhaité pour une
fréquence
-8
-10
-12
-14
-16
-0
-2
-4
-6
-8
-10
-12
-14
-16
2
-6
X
-16
-4
-0 -2 -4
-10
Y
1.00 0.95 0.90 0.85 0.80 0.75 0.70 0.65 0.60
0 2 4 6 8 10 12 14 16
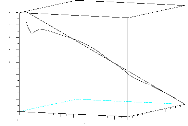
FIGURE 1.1 - Evolution de la position r du
centre de masse du sous-marin et de l'entrée
A3,3 de la matrice d'orientation. La cible est la
courbe (A(t),
r(t)) = (Id3,
--(t, t, t)) et la condition initiale pour les impulsions
est Ð0 = P0 = 0.
suffisamment grande des oscillations. Si l'approche
utilisée pour démontrer le théorème est
essentiellement du type boucle ouverte, les simulations montrent bien comment
le taux de convergence vers la trajectoire cible peut être
amélioré grâce à l'utilisation de termes correctifs
en boucle fermée.
Un exemple de suivi obtenu en appliquant cet algorithme (en
langage Scilab) est présenté dans la figure 1.1.
1.3 Propriétés de commandabilité d'une
classe de systèmes modélisant la nage de micro-organismes
[MS.3]
Dans cette section nous considérons un modèle de
dimension finie pour la nage d'un microorganisme dont la propulsion exploite
l'action d'un système de cilia couvrant sa surface. Les cilia
sont des cils vibratoires dont la taille est très petite par rapport
à celle du micro-organisme.
Un aspect fondamental des systèmes qui
modélisent la nage des micro-organismes est la forte viscosité
([26, 94, 111]). Cela permet de remplacer dans le modèle les
équations de Navier- Stokes qui décrivent l'évolution
temporelle du champ des vitesses du fluide qui entoure le microorganisme par
des équations de Stokes.
Le modèle pour la nage des micro-organismes couple
alors les lois de Newton régissant leur dynamique avec les
équations de Stokes. La description mathématique des
mécanismes de propulsion des micro-organismes (et donc du couplage entre
les lois de Newton et les équations de Stokes) a été
l'objet d'une riche littérature. Le mécanisme de propulsion
dépend bien sûr de l'espèce étudiée et donne
lieu à une grande variété de modèles (cf. par
exemple [10, 43, 59, 74]).
Le cas oil la propulsion est basée sur des cilia a
été décrit dans [27, 39, 59] et formulé comme un
système de contrôle de dimension finie par San Martín,
Takahashi et Tucsnak dans [101] (oil des premiers résultats de
contrôlabilité sont proposés). Le micro-organisme est
modélisé par un corps rigide et l'action des cilia par
une famille finie de m champs de vitesses sur sa surface qui
peuvent être directement contrôlés. Il est supposé
que le micro-organisme est entouré par un volume infini de fluide.
Le système de contrôle résultant est non
linéaire et défini dans un espace de dimension 12. Comme dans la
section précédente, les variables d'état sont les
coordonnées r E R3 du centre de masse de
l'organisme, son orientation A E SO(3), et
ses vitesses linéaire v E R3 et angulaire
|
ù ? R3. Le système a
la structure suivante :
|
|
|
zÿ
rÿ
|
=
=
|
Mz + E(z)
+ Bu, Av,
|
(1.4)
(1.5)
|
|
Aÿ
|
=
|
AS(ù),
|
(1.6)
|
|
où z = (v,
ù),
|
E(z) =
|
)
v ?
ù
J-1((Jù)
? ù)
|
et J est la matrice d'inertie du
micro-organisme. Les coefficients de la matrice 6 ×
6 M et de la matrice 6 × m B sont
obtenus, en resolvant des problèmes aux limites, à partir de la
forme du micro-organisme, de la distribution de sa masse et des champs de
vitesses decrivant l'action des cilia. La loi de commande
u est à valeurs dans Rm.
Une propriete importante du système ci-dessus est que
(1.4) est un système de contrôle bien defini dans R6,
ne dependant ni de r ni de A.
Rappelons qu'un système de contrôle
qÿ = F(q, u), u ?
U, est dit Lie bracket generating en un point
q si l'algèbre de Lie engendree par
{F(·, u) | u ? U}, evaluee
en q, est de rang maximal. On dit aussi, de façon
equivalente, que la famille de champs de vecteurs
{F(·, u) | u ? U} est Lie
bracket generating en q.
Nous avons le resultat suivant.
Proposition 1.9 Le système de
contrôle couplant (1.5),(1.6) et
zÿ = f(z,
u), z ? R6, u ?
Rm, (1.7)
est contrôlable si et seulement s'il est Lie bracket
generating en (z, r, A) = (0, Id3)
et si le système (1.7) est contrôlable.
Nous deduisons de la proposition 1.9 la genericite de la
contrôlabilite de (1.4)-(1.6) dans le sens suivant.
Théorème 1.10
Soit m = 3. Il existe alors un sous-ensemble ouvert
et dense O de {(M, B,
J) | J = JT >
0, M est symétrique et définie
négative
par rapport au produit scalaire associé à
diag(Id3, J)},
tel que (1.4)-(1.6) est commandable si (M,B,
J) ? O.
En particulier, il existe un sous-ensemble ouvert et
dense O de
{(Ù, Ø)
| Ù ? R3 ouvert connexe
borné non vide et de classe
C2, Ø ?
(C2(?Ù,R3))m}
par rapport à la topologie
C2 tel que si (Ù,
Ø) ? O alors le micro-organisme de forme
Ù et distribution de masse uniforme dont les champs de vitesses
contrôlés à la surface sont les composantes de
Ø est commandable.
Dans le cas où le micro-organisme est spherique et la
distribution de masse uniforme, nous avons que
M=
avec
-ñ1Id3 0
0 -ñ2Id3 ) ,
ñ2 >
ñ1 > 0.
Nous avons aussi que J est proportionnelle
à l'identité et donc
.
)
ù ? v
E(z) = 03
Notons par B1 et B2 les deux
matrices 3 × m telles que
)
B1
B = .
B2
Nous avons alors le résultat suivant.
Théorème 1.11 Supposons que
le micro-organisme soit de forme sphérique et que sa distribution de
masse soit uniforme. Alors (1.4)-(1.6) est commandable si et seulement si
B1 est non nulle et le rang de
B2 est égal à trois.
Chapitre 2
Contrôle quantique et propriétés
génériques de l'équation de
Schrödinger
2.1 Commandabilité de l'équation de
Schrödinger bilinéaire à spectre discret [MS.5]
Dans cette section, nous nous intéressons à la
commandabilité approchée de l'équation de Schrödinger
bilinéaire. Cette équation apparaît dans la
modélisation de nombreuses applications, parmi lesquelles la
résonance magnétique nucléaire, la spectroscopie laser et
l'informatique quantique (cf. [67, 91, 95, 103]). La commande agit sur le
système grâce à un champ extérieur; il peut s'agir
par exemple d'un champ magnétique ou d'un laser.
La question de la commande de la formulation fini
dimensionnelle de cette équation (qui s'applique aux systèmes de
spin ou quand une partie finie du spectre d'un système quantique est
très éloignée de son complémentaire) a
été l'objet d'une riche littérature (cf. par exemple [35,
36, 52] et les travaux qui y sont cités). Nous considérons ici
une équation de Schrödinger du type suivant
idø dt (t) =
(H0 +
u(t)H1)ø(t),
(2.1)
oh la fonction d'onde ø appartient
à un espace de Hilbert H de dimension infinie,
H0 est un opérateur auto-adjoint que l'on dit
hamiltonien non contrôlé,
u(t) est à valeurs dans un
sous-ensemble U de R et H1 est un
opérateur auto-adjoint responsable de l'interaction entre le
système et le champ extérieur.
Le cas type est celui oh H est égal
à L2(11, C) pour un certain
domaine 11 qui peut être égal soit à
Rd ou à un sous-domaine borné de
Rd et l'équation (2.1) est de la forme
i?ø ?t (t, x) =
(-Ä + V (x) +
u(t)W(x))
ø(t, x). (2.2)
Ici Ä denote le laplacien et V, W : 11
? R sont des fonctions mesurables et localement
bornées. Quand 11 est borné,
ø(t,.) satisfait des conditions de
Dirichlet au bord de 11. Les résultats présentés
ci-dessous s'appliquent aussi au cas oh 11 est une variété
riemannienne et Ä est l'opérateur de LaplaceBeltrami
correspondant.
Il est important pour les applications de pouvoir inclure dans
le modèle le cas oh W est non borné : le
potentiel W correspondant à une force extérieure
constante est en effet linéaire. La norme de l'opérateur de
multiplication par W sur Rd est
donc infinie.
Une propriété bien connue des équations
de type (2.2) est qu'elles ne sont jamais exactement commandables dans la
sphère unité de L2(11,
C) (cf. [15, 114]). Des résultats de non commandabilité,
même au sens approché, sont connus pour des situations
particulières ([83, 100]).
D'importants résultats positifs de
commandabilité ont été obtenus dans le cas
où d = 1, 11 est un segment et V = 0
([22, 24] ; cf. aussi [49]). Dans ces travaux, Beauchard et Coron ne
démontrent pas seulement la commandabilité approchée de
l'équation de Schrödinger, mais ils établissent aussi la
commandabilité exacte entre fonctions d'onde suffisamment
régulières. En particulier, ils obtiennent la
commandabilité exacte entre les états propres du hamiltonien non
contrôlé.
Des résultats de commandabilité approchée
dans le cas où le hamiltonien non contrôlé a un spectre
mixte ont été obtenus par Mirrahimi dans [81, 82] en utilisant
une technique de type Liapounov. Une technique similaire a été
appliquée par Nersesyan dans [87] dans le cas où le spectre est
discret. Les résultats de Nersesyan se rapprochent de ceux
présentés ci-dessous, même s'ils ne s'appliquent pas au cas
11 = Rd ni aux matrices de densité.
Signalons aussi que des résultats de commandabilité
ont été obtenus dans le même cadre dans le cas de plusieurs
contrôles (cf. [1, 29, 55]).
Nous supposons dans la suite que le spectre du hamiltonien non
contrôlé H0 est discret et nous le notons par
(ën)nEN (en répétant
chaque valeur propre en accord avec sa multiplicité). Notons par
(ön)nEN une base orthonormée
de H telle que chaque ön est
une fonction propre de H0 correspondant à la valeur
propre ën. Supposons aussi que
ön appartienne au domaine
D(H1) de H1 pour
tout n ? N. Il est alors possible de définir
H0 + uH1 sur V =
span{ön | n ? N} et de
l'étendre de façon unique à un opérateur
auto-adjoint sur H, noté par H0
+ uH1. Nous pouvons alors associer à une commande
constante u ? U l'évolution de (2.1) définie par
le groupe de transformation unitaires
e--it(H0+uH1) : H ?
H. Nous pouvons donc associer une solution
ø(· ;
ø0, u) à tout
u = u(·) constant par morceaux
et à toute condition initiale ø0 ?
H.
Rappelons la définition suivante :
Définition 2.1 Une
matrice C =
(cjk)1<j,k<n est dite connexe si,
pour tout paire d'indices j, k ? {1, . . . ,
n}, il existe une suite finie r1, .
. . , rl ? {1, . . . , n} telle que
cjr1cr1r2 · ·
· crl_1rlcrlk =6
0.
Rappelons aussi que les éléments de
(ën+1 - ën)nEN
sont linéairement indépendants sur Q
si, pour tous N ? N et
(q1,...,qN) ?
QN \ {0}, nous
avons ENn=1
qn(ën+1 - ën)
=6 0.
Nous pouvons démontrer le résultat suivant.
Théorème 2.2
Soient H0 et H1 comme
ci-dessus et U = (0,ä)
pour ä > 0. Supposons que les
éléments de (ën+1 -
ën)nEN sont linéairement
indépendants sur Q et que, pour tout n ?
N, la matrice
Cn = ~hH1öj,
ök)9-i)nj,k=1
est connexe. Alors (2.1) est commandable de façon
approchée sur la sphère unité de
H.
Remarquons qu'à la différence de la condition
sur l'indépendance linéaire sur Q des éléments de
(ën+1 - ën)nEN, la
condition sur la connexité des matrices Cn
peut dépendre de l'ordre choisi pour la suite
(ën)nEN. On peut montrer assez
simplement que si l'ordre est tel que Cn est
connexe pour une infinité de n ? N, alors il existe une
bijection h : N ? N telle que pour tout
n ? N la matrice
C71/1 = ((H1
öh(j),
öh(k))) 9-i j,k=1
est connexe. La réciproque n'est pourtant pas vraie.
La preuve du théorème 2.2 repose sur des
méthodes de dimension finie appliquées aux approximations de
Galerkin du système, dans le même esprit que dans [7, 99].
Notons Ed l'ensemble des ouverts connexes non
vides et bornés de Rd et définissons
E8d = Ed ?
{Rd}. Appliquons
maintenant le théorème 2.2 à l'équation (2.2) avac
11 ?
E8d . Sous les
hypothèses du théorème 2.3 ci-dessous, le
spectre de --A + V est discret (cf. [97]).
Notons ó(Ù, V ) =
(ëj(Ù, V ))j?N
la suite faiblement croissante de valeurs propres de --A
+ V , répétées en accord avec leur
multiplicité, et (öj(Ù, V
))j?N une suite de fonctions propres correspondantes
formant une base orthonormée de
L2(Ù, C). Sans perte de
généralité, nous pouvons supposer que
öj(Ù, V ) est à valeurs
réelles pour tout j E N. Si j E N est
tel que ëj(Ù, V ) est simple,
alors la fonction öj(Ù, V ) est
définie de façon unique quitte à la multiplier par
--1.
Théorème 2.3 Soit (i)
Ù E Ed, V, W E
L8(Ù) ou bien (ii) Ù =
Rd, V, W E
L8loc(Rd, R),
lim|x|?8 V (x)=
+oo et limsuplxi?8
log(|W(x)| +
1)/11x11 < oo. Supposons que
U contient l'intervalle (0, ä) pour
un certain ä > 0, que les elements de
(ëk+1(Ù,V ) --
ëk(Ù, V ))k?N sont
lineairement independant sur Q et qu'il existe une
bijection h : N N telle que pour tout n
E N la matrice
n
Chn(Ù,V,W)
= (L W
(x)öh(j)(Ù,
V
)öh(k)(Ù,
V ) dx)
j,k=1
est connexe. Alors (2.2) est commandable de façon
approchee sur la sphère unite de
L2(Ù, C).
Remarque 2.4 Demander que
ön appartienne à
D(H1) equivaut, dans le contexte de l'equation
(2.2), à ce que W
ön(Ù,V ) appartienne
à L2(Ù). Ceci est clairement
vrai dans le cas Ù E Ed.
Pour Ù = Rd, la propriete
decoule de l'hypothèse de croissance au plus exponentielle
de |W| à l'infini. Plus
precisement,
ea|x|ön(Rd,V
) E L2(Rd)
pour tous a > 0 et n E N
(cf. [2, 97]).
Les méthodes développées pour
démontrer le théorème 2.2 permettent en plus d'obtenir la
contrôlabilité approchée des matrices de densité.
Celles-ci décrivent l'état complet d'une famille
dénombrable de systèmes identiques avec conditions initiales
différentes, contrôlés simultanément par un seul
contrôle (cf. [9, 41]). Plus précisément, une matrice
de densite est un opérateur autoadjoint, borné et positif de
la forme
où (?j)j?N est une
base orthonormée de 1-1,
(Pj)j?N une suite de scalaires positifs tels
que E8j=1 Pj = 1 et
ø*(
·) =
(ø,
·) pour tout ø E 1-1.
Chaque ?j = ?j(t)
représente l'état d'une équation de Schrödinger de la
forme (2.1) et toutes ces équations sont asservies par la même loi
de commande constante par morceaux u =
u(t). L'évolution temporelle de la matrice de
densité ñ =
ñ(t) est donc décrite par
|
ñ(t) =
U(t;
u)ñ(0)U*(t;
u) =
|
X8
j=1
|
PjU(t;u)?j(0)(U(t;u)?j(0))*
(2.3)
|
où l'opérateur d'évolution
U(t; u) est défini par
U(t;
u)ø0 =
ø(t; ø0,
u) et U*(t;
u) dénote l'adjoint de U(t;
u).
Définition 2.5 Deux matrices de
densite ñ0 et
ñ1 sont unitairement equivalentes s'il existe une
transformation unitaire U de 1-1 telle
que ñ1 =
Uñ0U*.
Pour des systèmes quantiques fermés, le
problème de joindre deux matrices de densité par une trajectoire
admissible a sens seulement si les deux matrices sont unitairement
équivalentes. (La situation est différente pour des
systèmes ouverts ; voir par exemple [11].)
Le résultat suivant étend la commandabilité
approchée d'une équation de Schrödinger aux matrices de
densité correspondantes sous les mêmes hypothèses que
celles du théorème 2.2.
|
i
|
?ø(è,
t)
?t
|
=
|
?2
?è2
|
)+ u(t)
cos(è)ø(è,t).
(2.5)
|
Théorème 2.6 Soient
ñ0 et ñ1 deux
matrices de densité unitairement équivalentes. Alors, sous les
hypothèses du théorème 2.2, pour tout å
> 0 il existe une loi de commande u :
[0, T] ? U constante par morceaux telle
que Iñ1 - U(T;
u)ñ0U*(T;
u)I < å, où
1 · k dénote la norme des
opérateurs sur H.
Si la thèse du théorème 2.6 est
vérifiée on dit que (2.2) est commandable de façon
approchée au sens des matrices de densité. Le
théorème s'applique en particulier dans le cas H
= L2(Ù, C),
H0 = -L + V ,
H1 = W sous les hypothèses du
théorème 2.3.
2.2 Commandabilité de la rotation d'une
molécule quantique [MS.20]
L'orientation et l'alignement des molécules sont
d'importants domaines d'application du contrôle des dynamiques
moléculaires quantiques. Ils ont été l'objet d'une intense
activité de recherche à la fois du point de vue
expérimental et du point de vue théorique (cf. [102, 107] et les
références qui y sont citées).
Pour des molécules linéaires en phase gazeuse
contrôlées par des champs laser polarisés
linéairement, l'alignement correspond à maximiser la
probabilité que l'axe moléculaire soit parallèle à
l'axe de polarisation du laser. Pour les molécules
hétéronucléaires, un sens pour l'axe moléculaire
peut être défini. On dira que la molécule est
orientée si ce sens correspond à celui du vecteur de
polarisation. Alignement et orientation ont une variété
d'applications allant des réactions chimiques au traitement des
surfaces, des procédés de catalyse à la
nano-ingénierie.
Remarquons que la dynamique rotationnelle d'une
molécule est l'un des exemples les plus importants de système
quantique défini sur un espace d'Hilbert de dimension infinie et pour
lequel le spectre de l'opérateur de Schrödinger non
contrôlé est discret. Il s'agit donc d'un modèle
très naturel sur lequel appliquer les résultats
présentés dans la section précédente.
Nous nous focalisons ici sur la commande par champs laser de
la rotation d'une molécule rigide linéaire. Plus
précisément, nous considérons une molécule
linéaire polaire dans son état rovibronique fondamental sujette
à un champ laser polarisé qui n'est pas en résonance avec
ses fréquences vibroniques. Le but est de déterminer les
obstructions à la commandabilité dues aux symétries du
système et de démontrer la commandabilité approchée
entre tous les états ayant les mêmes propriétés de
symétrie. La commandabilité est obtenue pour des contrôles
arbitrairement petits, ce qui est intéressant du point de vue des
applications (cf. [108]).
La dynamique contrôlée est décrite par
l'équation de Schrödinger suivante sur la sphère
S2 (en choisissant des unités de mesure telles que
h = 1) :
|
i?ø(è,
ö, t)
?t
|
= (-BL -
u0E(t) cos
è)ø(è, ö,
t) (2.4)
|
où B est la constante rotationelle,
u0 est le moment dipolaire permanent, L est l'opérateur
de Laplace-Beltrami sur la sphère, è est l'angle
polaire entre la direction de polarisation et l'axe moléculaire et
ö est l'angle d'azimut. Le contrôle est
donné par le champ électrique E. Nous
négligeons dans ce modèle la contribution du tenseur de
polarisabilité qui correspond au moment dipolaire induit par le champ
électrique. L'approximation est correcte si l'intensité du laser
est suffisamment faible. Le modèle ainsi obtenu est certes
simplifié, mais il reproduit de façon très fidèle
les données expérimentales dans le cas des molécules
rigides (cf. [107]).
Nous allons simplifier ultérieurement le modèle
que l'on vient d'introduire en supposant que la molécule linéaire
reste sur un plan. L'équation de Schrödinger correspondante est
donc définie sur un cercle et prend, dans un système
normalisé de coordonnées, la forme suivante :
(Voir, par exemple, [105].) La commande est indiquee ici par la
lettre u.
Decomposons H =
L2(S1, C) dans
la somme directe Hp ? Hi, où
Hp et Hi sont, respectivement, les
sous-espaces des fonctions paires et impaires de H (la parite
etant consideree par rapport à è = 0).
Remarquons que Hp et Hi sont deux
espaces de Hilbert. Notons ø =
(øp, øi) la decomposition de
ø ? H avec øp ?
Hp et øi ? Hi.
Notre premier resultat sur la commandabilite de (2.5) est
negatif, affirmant que les normes des parties paire et impaire sont
conservees.
Proposition 2.7 Pour tout
ø0 appartenant à la sphère
unité de
L2(S1, C),
pour tout u dans
L8([0, T],
R) et pour tout t ? [0,T], nous
avons Iøp(t;
ø0, u)1H
=
lø0plH
et løi(t;
ø0, u)1H
=
1ø0i
1H.
Notre resultat principal est qu'il est possible de
contrôler simultanement la partie paire et celle impaire (de façon
approchee).
Théorème 2.8 Pour tous
ø0 =
(ø0 p, ø0 i
), ø1 =
(ø1p,
ø1i ) appartenant
à la sphère unité de
L2(S1,C)
qui vérifient
lø0p1H
=
Iø1p1H
et
1ø0i 1H
= 1ø1i
1H et pour tous å,ä > 0,
il existe T > 0 et u ?
L8([0, T], (0,
ä]) tels que

1ø1-ø(T;ø0,
u)11 <
å.
La demonstration est basee sur un argument de contrôle
simultane des systèmes quantiques pour lesquels l'union des spectres des
operateurs de Schrödinger forme une famille non resonante. Cet argument
est developpe de façon plus generale par Chambrion dans [42].
La condition de non resonance du spectre de l'operateur de
Schrödinger est testee en remplacant par
--a2/a02 cant +u
cos(è) avec u constant et en
exploitant la dependance analytique du spectre par rapport à
u et son expansion asymptotique etablie dans [58]. Le theorème
suivant, qui sera utilise à plusieurs reprises dans la suite de ce
chapitre, rappelle les proprietes d'analyticite de
ën(Ù, V ) et
ön(Ù, V ) par rapport
à V (cf. [69, 98]).
Théorème 2.9
Soient I ? R un intervalle ouvert et
Ù ? E8 d . Supposons
que V appartient à
V(Ù) et que u 7?
Wu est une courbe analytique de
I dans L8(Ù). Il
existe alors deux familles de fonctions analytiques
(Ëk : I ? R)k?N
et (Ök : I ?
L2(Ù))k?N telles que pour
tout u ? I la suite
(Ëk(u))k?N donne le
spectre (avec répétition des valeurs propres multiples)
de -A+V +Wu
et
(Ök(u))k?N est une
base orthonormée de fonctions propres correspondantes.
2.3 Généricité des
propriétés des fonctions et valeurs propres de l'équation
de Laplace-Dirichlet [MS.4]
Un espace topologique X est dit espace de
Baire si toute intersection denombrable de sous-ensembles ouverts et
denses de X est dense dans X. Tout espace
metrique complet est un espace de Baire. L'intersection denombrable de
sous-ensembles ouverts et denses d'un espace de Baire X est
dite un sous-ensemble résiduel de X. Une
fonction booleenne P : X ?
{0, 1}, où X
est un espace de Baire, est dite une propriété
générique s'il existe un sous-ensemble residuel
Y de X tel que chaque y ? Y
satisfait P, c'est-à-dire
P(y) = 1. Dans cette section et dans la suivante, le
rôle de X sera joue par differents espaces de
paramètres de l'equation de Schrödinger (2.2).
Soit Ù ? Ed. Les
resultats de la section 2.1 lient la commandabilite approchee de (2.2) aux
proprietes de W et des valeurs et fonctions propres de
l'operateur -A + V :
H2(Ù) n
H10(Ù) ?
L2(Ù). Pour demontrer que (2.2) est
generiquement contrôlable, nous sommes donc amenes à etudier, en
particulier, les proprietes spectrales generiques de -A
+ V .
Considerons d'abord l'independance lineaire sur Q des
differences des valeurs propres de -A + V .
Remarquons que, même si la propriete en question n'est pas verifiee par
les valeurs propres de -A + V , elle peut
l'être si l'on remplace V par V
+ uW pour un certain u tel
que (u, u + ä)
? U. La dependance du spectre de V +
uW par rapport à u etant analytique
(theorème 2.9), il serait alors suffisant de montrer que les derivees
de ën(Ù, V
+uW) par rapport à u evaluees
en u = 0 sont lineairement independantes sur Q. L'expression
de ces derivees est donnee par fn
W(x)ön(Ù,
V )2 dx, pourvu que la valeur
propre ën(Ù, V ) soit
simple. Dans le cas oil ën(Ù, V
) n'est pas simple, la formule de la derivee de
ën(Ù, V + uW)
par rapport à u reste vraie, mais le choix de la base
de fonctions propres (ön(Ù, V
))n?N depend alors de W (cf.
[8]).
Il est donc clair que si le spectre de
-Ä + V est simple et les carres de ses fonctions
propres forment une famille libre dans
L2(Ù), il existe alors W ?
L8(Ù) pour lequel les elements de (j
n W
(x)ön(Ù,
V )2 dx)n?N sont lineairement
independants sur Q. De plus, l'ensemble des W verifiant cette
propriete est residuel dans L8(Ù).
Remarquons que si le spectre de Ä est simple et les
carres de ses fonctions propres forment une famille libre dans
L2(Ù), alors la même propriete est vraie
pour -Ä + V pour un ensemble residuel
de V dans L8(Ù). Rappelons
que l'ensemble des domaines bornes Ù à bord
Cm pour lesquels le spectre de Ä est simple sur
Ù est residuel dans l'espace topologique
Óm des domaines bornes
Cm dote de la topologie
Cm, m = 1, (cf. [80, 115] et aussi
[65]).
Nous nous interessons donc à la question de la
genericite par rapport à Ù ?
Ók de l'independance lineaire des carres fonctions
propres de Ä. Notons
ënn =
ën(Ù, 0) et
önn =
ön(Ù, 0) pour tout n
? N. Nous indiquons par D0,1
l'ensemble des domaines de Rd qui peuvent
être transformes dans la boule unite de Rd
par un homeomorphisme bi-lipschitzien. En particulier, le bord d'un element
de D0,1 est lipschitzien.
Nous pouvons demontrer le resultat general suivant.
Théorème 2.10
Soit Fn :
Rn(n+1) -? R
une suite de fonctions analytiques. Pour tout n ?
N et pour tout domaine borné Ù
? Rd à bord lipschitzien, nous
dirons que Ù satisfait la propriété
Pn si
ën1 , ... ,
ënn sont simples et
s'il existe n points
x1, . . . , xn dans Ù
et un choix de ön1 ,
... , önn tels
que
Fn(ön1
(x1), . . . ,
önn
(x1), . . . , ön1
(xn), . . . ,
önn
(xn),
ën1 ,... ,
ënn) =6
0.
Si, pour tout n ? N, il
existe Rn ? D0,1 qui
satisfait la propriété Pn,
alors pour tout m ? N ?
{+8} l'ensemble des Ù
? Óm satisfaisant
Pn pour tout n ? N est
résiduel dans Óm.
La demonstration est basee sur un resultat de dependance
analytique du spectre de l'operateur de Laplace-Dirichlet par rapport au
domaine, analogue au theorème 2.9. Un autre resultat crucial pour la
preuve, du à Teytel, est la possibilite de deformer analytiquement deux
domaines reguliers isotopes en imposant la simplicite du spectre le long de la
deformation ([113]).
Nous deduisons du theorème 2.10 les consequences
suivantes.
Corollaire 2.1 Soit m
? N ? {8}. Alors, pour tout Ù
dans un ensemble résiduel de
Óm, les carrés des
fonctions propres de l'opérateur de Laplace-Dirichlet sur
Ù sont linéairement indépendants.
Corollaire 2.2 Soient m
? N ? {8}, k ? N
et q = (q1, . . . ,
qk) ? Rk \
{0}. Alors, pour tout Ù dans un
ensemble résiduel de
Óm,
En particulier, les éléments du spectre de
l'opérateur de Laplace-Dirichlet sur Ù sont
génériquement linéairement indépendants sur
Q.
Concernant l'equation de Schrödinger bilineaire, nous
deduisons des arguments presentes au debut de cette section les resultats
suivants.
Proposition 2.11 Génériquement
par rapport à (Ù, W) ?
Óm ×
L8(Rd),
l'équation
i?ø ?t (t,x) =
(-Ä +
u(t)W(x))
ø(t,x)
est commandable de façon approchée sur la
sphère unité de
L2(Ù).
Proposition 2.12
Génériquement par rapport à
(Ù, V, W) ?
Óm ×
L8(Rd) ×
L8(Rd), l'équation
(2.2) est commandable de façon approchée sur la sphère
unité de L2(Ù).
2.4 Généricité par rapport aux
potentiels de la commandabilité de l'équation de Schrödinger
bilinéaire à spectre discret [MS.1]
Dans cette section, nous nous intéressons à la
généricité de la commandabilité de
l'équation de Schrödinger (2.2) par rapport au potentiel de
contrôle W et à celui non contrôlé
V , dans le but d'améliorer les résultats des
propositions 2.11 et 2.12. Nous nous plaçons dans le cas d'une
équation de Schrödinger à spectre discret définie sur
un domaine Ù ? Î8 d .
Rappelons que la question de la
généricité par rapport aux potentiels de la
commandabilité de l'équation de Schrödinger
bilinéaire a déjà été l'objet de certains
résultats obtenus par Nersesyan : en particulier [87, lemme 3.12]
démontre la généricité par rapport au couple
(V, W) de la contrôlabilité approchée de
(2.2) quand d = 1 et Ù est borné (sous des
hypothèses de régularité sur V et
W). D'autres résultats intéressants de
généricité pour la contrôlabilité d'une
équation de Schrödinger linéarisée ont
été obtenus par Beauchard, Chitour, Kateb et Long dans [21] et
sont présentés plus en détail dans la discussion à
la fin de cette section.
L'approche que nous proposons ici est de la même nature
que celle exploitée dans la section précédente : nous
appliquons des perturbations analytiques à longue distance des
paramètres et nous exploitons la dépendance analytique par
rapport à V et W des objets
mathématiques qui apparaissent dans les hypothèses du
théorème 2.3 (cf. théorème 2.9).
Pour tout Ù ? Î8 d
, soit V(Ù) égal à
L8(Ù) si Ù ?
Îd et à {V ? L8
loc(Rd) | lim11x11?8 V
(x) = +8} si Ù =
Rd. Dans les deux cas, dotons
V(Ù) de la topologie L8.
Introduisons aussi l'espace W(Ù), donné par
L8(Ù) si Ù ?
Îd et par
|
{W ? L8 loc(Rd) |
sup
x?Rd
|
log(|W(x)|
+ 1)< 8} IxI + 1
|
|
si Ù = Rd. Dotons
W(Ù) de la topologie L8.
Notons
Z(Ù,U) =
{(V,W) | V ?
V(Ù), W ? W(Ù),V +
uW ? V(Ù) ?u ? U, sup
x?Ù
|
|W(x)|
|V (x)| + 1
< 8}
|
et équipons Z(Ù,
U) avec la topologie L8. Introduisons
aussi, pour tout V ? V(Ù) et tout W ?
W(Ù), les sous-espaces topologiques de
V(Ù) et W(Ù) définis
par
V(Ù,W,U) = {
V ? V(Ù) | (
V , W ) ?
Z(Ù, U)}, W(Ù,
V, U) = { W ? W(Ù)
| (V, W ) ?
Z(Ù, U)}.
Remarquons que V(Ù, W,
U) et W(Ù, V, U) sont tous
les deux non vides et invariants par rapport à la somme avec
L8(Ù). En particulier, ils sont ouverts dans
V(Ù) et W(Ù) respectivement et
coïncident avec L8(Ù) quand Ù
est borné.
Nous dirons que le triplet (Ù, V, W)
est apte à contrôler si V ?
V(Ù), W ? W(Ù), les
éléments de la suite
(ëk+1(Ù, V ) -
ëk(Ù, V ))k?N sont
linéairement indépendant sur Q et s'il existe un
bijection h pour laquelle
Chn(Ù, V, W) est connexe
pour tout n ? N.
Nous dirons aussi que le quadruplet (Ù, V, W,
U) est efficace si (V, W) ?
Z(Ù, U) et s'il existe u
et ä > 0 tels que (Ù, V
+ uW, W) est apte à contrôler et (u,
u + ä) ? U. Les
théorèmes 2.3 et 2.6 peuvent alors être reformulés
ainsi : l'efficacité du quadruplet (Ù, V, W, U)
est une condition suffisante pour la contrôlabilité
approchée au sens des matrices de densité.
Nous pouvons démontrer le résultat de
continuité suivant.
Proposition 2.13 Soit Ù =
Rd. Supposons que V
appartient à
V(Rd), que
ëk(Rd, V ) est
simple et que W ?
L8loc(Rd,R)
est tel que la croissance de |W| est au plus
exponentielle à l'infini. Il existe alors un voisinage
N de V dans
V(Rd) tel que
ëk(Rd,V ) est
simple pour tout V ? N et V 7?
V|W|ök(Rd, V )
(définie au signe près) est continue comme fonction
de N dans
L2(Rd).
La preuve est basée sur l'uniformité des
estimées obtenues par Agmon dans [2] (théorèmes 4.1, 4.3
et 4.4).
Un premier résultat de généricité
par rapport à V est le suivant, qui
généralise un résultat classique de Albert ([8]).
Proposition 2.14 Soit Ù un
élément de
Î8d et
notons, pour tout k ? N,
Rk(Ù) = {V ?
V(Ù) | ë1(Ù,V
),...,ëk(Ù, V ) sont
simples}. Pour tous K ? N
et q = (q1,...
,qK) ? RK \
{0}, l'ensemble
|
Oq(Ù) =
|
?
?
?
|
V ? RK(Ù) |
|
XK
j=1
|
qjëj(Ù, V )
=6 0
|
}
|
est ouvert et dense dans
V(Ù). Par conséquent, génériquement
par rapport à V les élément de
(ën(Ù, V
))n?N sont linéairement indépendants
sur Q.
La preuve de la proposition 2.14 est basée sur le lemme
suivant.
Lemme 2.15 Soient Ù un
élément de
Î8d
et ù un ensemble non vide, ouvert,
compactement contenu dans Ù et dont le bord est lipschitzien.
Soient v un élément de
L8(ù) et
(Vk)k?N une suite dans
V(Ù) telle que Vk|ù ? v
dans L8(ù)
quand k ? 8 et limk?8
infÙ\ù Vk = +8.
Alors, pour tout j ? N, limk?8
ëj(Ù, Vk) =
ëj(ù,v). De plus, si
ëj(ù,v) est simple alors
limk?8 öj(Ù,Vk) =
öj(ù, v) (au signe
près) dans L2(Ù).
Si ëj(ù,v)
et ëm(ù,v)
sont simples, alors (au signe près)
lim f2 Vieöj
(Ù,
Vk)öm(Ù, Vk)
= f vöj (ù,
v)öm(ù,
v).
S ca
k?8
Nous déduisons de la proposition 2.14 le résultat
suivant.
Proposition 2.16 Soit Ù un
élément de
Î8d . Alors,
génériquement par rapport à (V,
W) ? Z(Ù,
U), le triplet (Ù,V,W) est apte
à contrôler.
En étudiant la généricité par rapport
à V ou W seulement, nous pouvons
démontrer les deux propositions suivantes.
Proposition 2.17 Soient Ù
un élément de
Î8d
et W ? W(Ù) non constant et absolument continu
sur Ù. Alors, génériquement par rapport
à V dans
V(Ù,W,U), le quadruplet
(Ù, V, W, U) est efficace.
Proposition 2.18 Soient Ù
un élément de Î8 d et
V ? V(Ù) absolument continu sur
Ù. Supposons que l'intérieur de U
est non vide. Alors, génériquement par rapport
à W ? W(Ù, V, U), le
quadruplet (Ù, V, W, U) est efficace.
Il est naturel, au vu des résultats
présentés dans cette section et dans la précédente,
de se demander si l'équation (2.2) est commandable de façon
approchée génériquement par rapport à Ù
? Îd, quand V et
W sont fixés. Une conjecture dans ce sens est
raisonnable (sous l'hypothèse que W soit non constant
sur chaque ouvert non vide) mais les techniques employées ici paraissent
difficiles à adapter dans ce cas. Une difficulté vient du fait
que la dépendance de
ëk(Ù, V ) par
rapport à Ù n'est pas analytique si V ne l'est
pas. De façon similaire, les quantités
f
Wök(Ù, V
)öj(Ù, V ) ne varient
pas, en général, analytiquement par rapport à Ù. Un
résultat
partiel dans le cas V = 0 allant dans la
bonne direction a été démontré dans [21], oh les
auteurs prouvent que pour W ?
C1(R2, R) non constant sur
chaque ouvert non vide, pour un domaine C3
générique Ù ? R2 nous avons
j W ö1(Ù,
0)öj(Ù, 0) =6
0 pour tout j ? N. La preuve proposée dans
[21] est très technique et délicate : son extension dans le cas
oh V est quelconque et d > 2 parait une
tache ardue.
Chapitre 3
Stabilité et stabilisation des systèmes
hybrides
3.1 Stabilité des systèmes à
commutations non linéaires sur le plan [MS.9]
Un système à commutations est une famille
de systèmes dynamiques équipée d'une loi qui
détermine à tout moment quelle dynamique est responsable de
l'évolution temporelle.
Dans le cas des systèmes en temps continu, un
système à commutations peut s'écrire sous la forme
qÿ =
fá(q), q ? M,
á ? I, (3.1)
où I est un sous-ensemble mesurable de
R, M est une variété différentielle et
F = {fá | á ? I} est
une collection de champs de vecteurs sur M. Si la forme est la
même que celle d'un système de contrôle,
l'interprétation est différente : nous voulons déterminer
des propriétés sur l'évolution du système qui ne
dépendent pas de la loi de commutation, qui est une fonction
á : [0, 8) ? I
appartenant à un sous-ensemble G de
L8([0, 8), I)
(cf. [73]).
Dans cette section, nous nous intéressons en
particulier au problème suivant : si un point q0 de
M est globalement asymptotiquement stable pour chaque
fá, quelles autres conditions sur F
sont nécessaires pour garantir que q0 soit
globalement asymptotiquement stable pour (3.1) indépendamment et
uniformément par rapport au choix de la loi de commutation
á ? G ?
Plus précisément, nous nous intéressons ici
aux systèmes à commutations non linéaires du type
qÿ = á
X(q) + (1 - á)Y
(q), q ? R2 ,
á ? {0,1}, (3.2)
où les deux champs de vecteurs X et
Y sont lisses et G =
L8([0, 8),
{0, 1}). Nous supposons que
X(0) = Y (0) = 0 et que les deux
systèmes dynamiques qÿ =
X(q) et qÿ = Y
(q) sont globalement asymptotiquement stables
à l'origine. Nous cherchons des conditions sur X et
Y (faciles à vérifier et invariantes par petites
perturbations) telles que le système (3.2) soit globalement
uniformément asymptotiquement stable à l'origine par rapport
à á ? L8([0,
8), {0, 1}) (GUAS
dans la suite), c'est-à-dire si, (i) pour tout ä >
0 il existe å > 0 tel que toute trajectoire
de (3.2) démarrant d'un point de norme inférieure à
å reste dans la boule de centre l'origine et rayon
ä et (ii) pour tous ä1,
ä2 > 0, il existe T > 0
tel que l'évaluation au temps T d'une quelconque
trajectoire de (3.2) démarrant d'un point de norme inférieure
à ä1 ait norme inférieure à
ä2.
Notons
Z = {q ?
R2 |
dim(span(X(q),Y
(q))) < 2}.
Un premier résultat que nous pouvons démontrer est
le suivant.
Théorème 3.1 Si Z
est compact, alors (3.2) est uniformément stable par
rapport à á. Si, en plus,
Z = {0} alors (3.2)
est GUAS.
D'autres conditions peuvent être obtenues en tenant compte
de la position relative de X et
Y le long de Z. En
particulier, il est facile de voir que s'il existe une composante connexe de
Z \ {0} sur laquelle X
et Y pointent de façon opposée, alors
(3.2) n'est pas GUAS.
Introduisons l'hypothèse suivante, qui est
générique dans la classe des couples de champs de vecteurs
globalement asymptotiquement stables à l'origine (au sens de la
topologie C2) : nous disons que (X, Y
) satisfait l'hypothèse (h0) si (i)
Z \ {0} est une sous-variété
immergée de R2, (ii) X et Y
changent orientation en traversant Z et (iii)
X et [X, Y ] ne sont pas colinéaires
aux points de Z \ {0} auxquels X
est tangent à Z.
Théorème 3.2 Soit
(X, Y ) une couple de champs de vecteurs globalement
asymptotiquement stables à l'origine satisfaisant l'hypothèse
(h0). Alors : (A) si l'origine est isolée dans
Z et X n'est nulle part
tangent à Z \ {0}, alors
(3.2) est GUAS; (B) si Z \ {0}
contient une composante connexe non bornée sur laquelle
X et Y pointent de
façon opposée, alors (3.2) admet des trajectoires qui
divergent.
La figure 3.1 donne, graphiquement, la clé de la preuve
de l'énoncé (A). Les courbes Tj indiquent les
composantes connexes de Z \{0}. Nous
considérons les deux trajectoires démarrant de q
et qui commutent à chaque croisement de Z.
Nous montrons qu'elles convergent vers l'origine et que le champ de vecteurs
X + Y pointe toujours à
l'intérieur de la région bornée qu'elles délimitent
(sauf, éventuellement, à l'origine). Nous pouvons ainsi exclure
toute intersection des deux trajectoires en dehors de la composante connexe de
R2 \ ?jTj qui contient l'origine.
Nous concluons en utilisant la structure ainsi caractérisée de
l'ensemble des points atteignables à partir de q par
des trajectoires admissibles de (3.2).
T4
0
X
Y
X
Y
0
Y
X
T3
Y
T3
X
Y
X
T2
X
T2
X
Y
Y
Y
Y
X
q
X
q
T1
T1
FIGURE 3.1 Idée de la preuve du théorème
3.2, énoncé (A)
3.2 Systèmes soumis à une condition
d'excitation persistante [MS.6,23]
Nous étudions dans cette section des systèmes de
contrôle du type
xÿ = Ax +
á(t)bu, x ?
Rd, (3.3)
oh A est une matrice n ×
n, b est un vecteur de
Rd, (A, b) est un couple
commandable, la commande u est scalaire et á
est une loi de commutation dépendant du temps à valeurs
dans l'intervalle [0, 1] qui satisfait une condition
d'excitation persistante du type
|
Z t+T
t
|
á(s)ds = 1a,
pour tout t = 0, (3.4)
|
oh 0 < 1a = T sont indépendants de
t.
A 1a et T donnés, notons
G(T, 1a) l'ensemble des á
: [0, 8) ? [0, 1]
mesurables qui satisfont (3.4). Un élément de
G(T, 1a) est dit un (T,
1a)-signal.
Nous disons qu'un vecteur K est un
(T, 1a)-stabilisateur si le retour d'état
u = -Kx stabilise (3.3) à l'origine,
uniformément par rapport à tous les éléments de
G(T, 1a). Plus précisément,
K ne peut dépendre que de A, b, T, 1a
et pas de á. La question de l'existence d'un
(T, 1a)-stabilisateur a son origine dans des problèmes
d'identification et commande adaptative (cf. [12]). La condition d'excitation
persistante peut aussi modéliser des contraintes sur l'action de
stabilisation qui dépendent de phénomènes
périodiques ou quasi-périodiques. Elle peut aussi être
utilisée pour étudier des situations dans lesquelles le
contrôleur n'a pas la possibilité, par moments, d'agir sur le
système (par exemple, à cause d'interruptions de la transmission
entre le contrôleur et l'actionneur) et il n'est pas possible de savoir
a priori à quels instants cela arrivera, mais seulement de
garantir que cela n'arrivera pas « trop souvent ».
Nous nous intéressons en particulier au cas oh la
matrice A n'est pas stable. Il paraît difficile dans
cette situation d'utiliser des méthodes de type Liapounov. Nous avons
donc développé une méthode démonstrative par
contradiction qui permet d'associer, par une procédure asymptotique, un
système à commutations au système excité. En
démontrant que ce système limite est stabilisable, nous obtenons
la (T, 1a)-stabilisabilité du système
excité. La stabilisabilité du système à
commutations est prouvée en généralisant un
résultat d'observabilité uniforme obtenu par Gauthier et Kupka
dans [60].
Nous obtenons ainsi le résultat suivant.
Théorème 3.3 Soit
(A, b) commandable et supposons que toutes les
valeurs propres de A sont à partie
réelle inférieure ou égale à zéro. Alors,
pour tout T, 1a avec T = 1a >
0 il existe un (T, 1a)-stabilisateur de
(3.3).
Pour tout (A, b) commandable, pour tout
K dans Rd, pour tous T, 1a
avec T = 1a > 0, et pour tout á ?
G(T, 1a), soit
ë+(á, K) l'exposant
maximal de Liapounov associé à xÿ =
(A - ábKT)x, à
savoir :
|
ë+(á,
K) = sup lim sup
11x011=1
t?+8
|
log(kx(t; 0,
x0, K, á)I)
|
|
|
t
|
.
|
Ici x(t; 0,
x0, K, á) indique l'évaluation au temps
t de la solution de xÿ = (A -
ábKT)x avec condition initiale
x0 au temps 0.
Le taux de convergence associé à
(A, b, T, 1a, K) est défini par
tc(A,b,T,1a,K) = - sup
ë+(á,
K).
á?G(T,u)
Les changements de variables linéaires n'affectent pas les
exposants de Liapounov et donc tc(A, b, T, 1a, K) =
tc(PAP -1, Pb, T, 1a,
(P-1)TK),
(3.5)
pour toute matrice inversible P.
Le taux maximal de convergence associé
à xÿ = Ax +
ábu, á ? G(T, pi), est
défini par
|
TC(A, T, pi) = sup
K?Rd
|
tc(A, b, T, pi, K).
|
Il ne dépend pas de b à cause de
(3.5) (on peut toujours transformer le système en forme compagnon par un
changement linéaire des variables).
Proposition 3.4 Il existe
ñ* ? (0, 1) (ne
dépendant que de d) tel que pour tout
(A, b) commandable, pour tout T >
0 et tout ñ ?
(ñ*,1] nous avons TC(A,T,
ñT) = +8.
La proposition précédente peut être
démontrée par un argument de type grand gain. Dans le cas
d = 2, nous pouvons obtenir le résultat complémentaire
suivant.
Proposition 3.5 Soit d
= 2. Il existe ñ* ?
(0, 1) tel que pour tout (A, b)
commandable, pour tous T > 0 et
ñ ? (0, ñ*), nous
avons TC(A,T, ñT) <
+8.
Nous ne sommes pas en mesure d'établir si la
proposition 3.5 peut être généralisée au cas
d > 2. La technique à la base de notre preuve n'est
pas facilement généralisable, reliant sur la construction
explicite de certaines courbes dans le plan. Nous croyons, néanmoins,
qu'il soit raisonnable de conjecturer l'extensibilité du résultat
au-delà de la dimension deux.
Une conséquence de la proposition 3.5 est l'existence
d'une matrice A telle que, si pi/T <
ñ*, le système (3.3) n'admet pas de
(T, pi)-stabilisateur. Nous pouvons prendre, par exemple,
( ë 1 ) 0
)
A = , b =
0 ë 1
avec ë suffisamment grand.
L'intérêt de cette propriété vient de sa
compatibilité avec les trois faits suivants : primo, toute limite
faible-? dans
L8([0,
+8), [0, 1]) d'une suite
(án)n?N avec
án ? G(Tn,
ñTn) et limn?+8
Tn = 0 est à valeurs dans
[ñ,1]; deuxio, la topologie faible-?
rend l'application entrée-sortie á 7?
x(t; 0, x0, K,
á) continue ; tertio, le système à
commutations
xÿ =
0 1 )
x + á?bu
0 0
peut être stabilisé, uniformément par
rapport à á? ?
L8([0,
+8), [ñ, 1]), avec un
taux de décroissance arbitrairement grand. Une conjecture à
priori plus faible (mais probablement équivalente) de celle concernant
l'extensibilité de la proposition 3.5 au cas d > 2
est qu'il existe, en toute dimension supérieure à deux, un couple
commandable (A, b) et des valeurs 0 < pi =
T tels que (3.3) n'admet pas de (T,
pi)-stabilisateur.
La constante qui discrimine entre taux de convergence
arbitrairement grand et taux de convergence borné peut être
étudiée en fonction de A et T.
Soit
ñ(A,T) =
inf{ñ ? (0,1] |
TC(A, T, T ñ) = +8}. (3.6)
Remarquons que ñ(A,T)
est égal à ñ(A/T, 1) et
ne dépend pas de la trace de A. La définition
de ñ et le résultat qui suit sont valables
pour d ? N quelconque.
Lemme 3.6 La fonction T 7?
ñ(A, T) est localement Lipschitz sur
(0, +8). Les deux limites
limT?+8
ñ(A,T) et
limT?0+ ñ(A,T)
existent et sont égales, respectivement, à
supT>0
ñ(A,T) et
infT>0
ñ(A,T).
Le comportement de la fonction ñ est
loin d'être complètement compris et suscite des nombreux
problèmes ouverts et conjectures. Par exemple : quelles sont les
matrices A pour lesquelles T 7?
ñ(A,T) est constante ? Est-ce que la valeur
constante de ces fonctions dépend de A? Si oui, comment
? La même question de l'éventuelle dépendance par rapport
à A se pose pour les limites
limT?0+ ñ(A,T) et
limT?+8 ñ(A,T).
3.3 Analyse de stabilité des systèmes
linéaires à commutations à temps discret par le biais de
fonctions de Liapounov quadratiques [MS.27]
Nous considérons dans cette section la stabilité
uniforme de systèmes a commutation linéaires a temps discret du
type
x(k + 1) =
Aî(k)x(k),
k ? N, (3.7)
où la suite x est a valeurs dans
Rd. Les matrices Aî, de
taille d × d, dépendent d'un paramètre
î ? ? RM qui varie en
fonction du temps (discret).
L'intérêt principal de ce type de systèmes
est son aptitude a modéliser des situation où la dynamique est
sujette a perturbations dépendantes du temps trop difficiles a
décrire précisément, mais que l'on peut borner (cf. [73,
96]).
La stabilité d'un système du type (3.7) peut
être caractérisée grâce au rayon spectral conjoint
([32, 93]). Celui-ci n'étant pas calculable exactement en un nombre fini
de pas, il en résulte que l'analyse de stabilité de (3.7) reste
un problème ouvert, même dans le cas d = 2. (La
situation est différente dans le cas des systèmes a temps continu
: voir [34] et [14] pour une classification des systèmes globalement
uniformément stables et aussi [5] pour la réduction au cas
d = 2 d'une classe de systèmes de dimension
supérieure.)
La recherche de critères viables pour tester la
stabilité de ces systèmes a donné lieu récemment a
une intense activité scientifique (cf., par exemple, [28, 61] et les
références qui y sont citées).
Un des critères les plus populaires est celui de la
stabilité dite quadratique, qui correspond a l'existence d'un
fonction de Liapounov quadratique V (x) =
xTPx commune a toutes les dynamiques
Aî (cf. [20]). Nous appellerons dans la suite cette
stabilité quadratique statique. L'avantage pratique de ce type
de critère est qu'il peut être reformulé de façon
équivalente en termes d'inégalités matricielles
linéaires (LMI dans l'acronyme anglais utilisé habituellement)
qui peuvent être testées par des solveurs classiques ([38]).
Le critère de stabilité quadratique statique
peut être étendu au cas où la fonction de Liapounov
dépend du paramètre î, prenant la forme
V (x, î) =
xTP(î)x
(cf. [56]). On parle alors de stabilité quadratique
dépendant des paramètres. Dans le cas où les matrices
Aî appartiennent a un polytope, î 7?
Aî est une paramètrisation affine et l'application
î 7? P(î) est contrainte a
être affine, l'existence d'une telle fonction de Liapounov peut a nouveau
se tester grâce a des LMI ([50]).
La contribution présentée ici a pour but de
garantir que la structure imposée a î 7?
P(î) dans [50] n'est pas contraignante par
rapport a celle plus général de la stabilité quadratique
dépendant des paramètres, dans le sens que si A(
) est un polytope convexe et une fonction de Liapounov dépendante de
î existe, alors il en existe une qui est affine (et sa
recherche peut donc être effectuée par le biais d'une LMI). Nous
montrons aussi que, même en rajoutant une dépendance explicite de
P par rapport au temps k, la classe de
systèmes dont la stabilité peut être testée
grâce a P ne croît pas.
Definition 3.7 Nous disons que (3.7) est
uniformément asymptotiquement stable si, pour tout
x0 ? Rd,
la solution de (3.7) avec condition initiale x(0) =
x0 converge à zéro uniformément par
rapport à {î(k)}k?N
? et si, pour tout R > 0, il existe
r > 0 tel que, pour tous
Ix(0)I < r,
{î(k)}k?N ?
et k ? N, nous avons
Ix(k)I <
R.
Une condition suffisante pour la stabilité uniforme
asymptotique de (3.7) est la suivante.
Definition 3.8 Nous disons que (3.7)
satisfait la propriété de stabilité quadratique
dépendant des paramètres (SQDP) s'il existe
á0,á1,á2
> 0 et
V (x, î) =
xTP(î)x
(3.8)
tels que
á1IxI2 =
V (x, î) =
á2kxk2
et, pour tous x(0) ?
Rd,
{î(k)}k?N ?
et k ? N, nous avons
V (x(k +
1), î(k + 1)) - V
(x(k),
î(k)) =
-á0Ix(k)I2.
La souplesse de la propriété SQDP est
donnée par le fait qu'elle autorise P à
dépendre du temps, par le biais du paramètre de commutation
î. Nous pouvons obtenir une autre condition suffisante,
a priori plus générale, pour la stabilité uniforme
asymptotique de (3.7) en ajoutant dans P la dépendance
explicite par rapport au temps.
Définition 3.9 Nous disons que (3.7)
satisfait la propriété de stabilité quadratique
dépendant des paramètres et du temps (SQDPT) s'il existe
á0,á1,á2
> 0 et
V (k, x,î) =
xTP(k,
î)x
tels que
á1IxI2 =
V (k,x, î) =
á2kxk2
et, pour tous x(0) ?
Rd,
{î(k)}k?N ?
et k ? N, nous avons
V (k + 1,
x(k + 1), î(k
+ 1)) - V (k,
x(k),
î(k))=-á0
Ix(k)
12.
Soit le simplexe conv{e1,... , eM}
de RM, où
{e1,... , eM} dénote la base
canonique. Nous supposons dans la suite que A est de la
forme
A(î) =
XM îiAi.
i=1
Nous disons que V , définie par (3.8),
est polyquadratique si P(î)
est linéaire par rapport à î.
Remarque 3.10 Le système (3.7) est
uniformément asymptotiquement stable si et seulement si cela est vrai
pour le système où est remplacé par
{e1,... , eM}. En effet, en
utilisant la convexité de la norme des matrices, il est possible de
vérifier que le rayon spectral conjoint des deux systèmes est le
même.
L'équivalence entre les différentes notions de
stabilité quadratique est énoncée dans le
théorème suivant.
Théorème 3.11 Soient =
conv{e1,...,eM} et
A(î) = PM i=1
îiAi pour î ? .
Alors (3.7) satisfait la propriété de SQDPT si et seulement s'il
satisfait la propriété de SQDP avec V
polyquadratique.
Nous pouvons aussi montrer que la stabilité asymptotique
uniforme n'est pas équivalente à la stabilité quadratique,
dans le sens suivant.
Proposition 3.12 Il existe des
systèmes du type (3.7) qui sont uniformément asymptotiquement
stables mais qui ne satisfont pas la propriété de SQDP.
L'équivalent de la proposition 3.12 dans le cas
à temps continu avait déjà été
remarqué (cf. [53, 78]). Le passage au cas du temps discret peut se
faire en discretisant un système à commutions à temps
continu vérifiant GUAS et n'admettant pas de fonction de Lyapounov
quadratique commune et en faisant tendre le pas de discretisation temporelle
vers zéro.
Chapitre 4
Géométrie presque riemannienne
[MS.2,8,15]
Soient M une variété lisse de
dimension deux et X, Y deux champs de vecteurs lisses sur
M. Si {X, Y } est Lie bracket generating,
alors le système de contrôle
qÿ =
uX(q) + vY
(q), u2 +
v2 = 1, q ? M ,
(4.1)
est commandable et la fonction valeur pour le temps minimum
définit une distance continue sur M. Dans le cas
où X et Y sont partout
linéairement indépendants (ce qui peut arriver seulement si
M est parallélisable), la distance ainsi obtenue est
riemannienne et correspond à la métrique pour laquelle
(X, Y ) est un repère mobile orthonormal.
Dans cette section, nous nous intéressons à la
géométrie obtenue dans le cas où les deux champs de
vecteurs peuvent être colinéaires à certains points.
Une structure métrique sur une surface M
est dite presque riemannienne si elle peut être
définie localement par un couple de champs de vecteurs (X, Y
) grâce à (4.1). De façon plus intrinsèque,
une structure presque riemannienne S est un couple (E,
f), où E est un fibré euclidien de rang
deux sur M et f : E ? TM est
un morphisme de fibrés vectoriels tel que
f(Eq) ? TqM
et l'évaluation en q de l'algèbre de
Lie engendrée par
L = {f ? ó | ó section de
E}
est égale à TqM pour
tout q ? M. (La notion de structure presque riemannienne
s'étend naturellement au cas d'une variété
différentielle de dimension supérieure à deux).
Si E est orientable, nous disons que S
est orientable. Si E est équivalent
au fibré euclidien trivial M × R2, nous
disons que la structure presque riemannienne est trivialisable.
Notons par Z, dit ensemble
singulier, l'ensemble des points q de M
tels que f(Eq) est de
dimension un. Sous des hypothèses de généricité sur
f, l'ensemble Z est une
sous-variété de dimension un de M. Une structure
presque riemannienne est riemannienne si et seulement si Z =
Ø, c'est-à-dire, f est un
isomorphisme de fibrés vectoriels. Un couple de champs de vecteurs
(X, Y ) de L est dit une base orthonormale de
S sur un ouvert 11 de M si X
= f ? ó et Y =
f?ñ avec (ó, ñ) une base
orthonormale pour E sur 11. Les bases orthonormales de
S forment un système de générateurs
locaux de L. Remarquons que S est trivialisable si et
seulement s'il existe une base orthonormale globale de S.
Un exemple célèbre de structure presque
riemannienne est le plan de Grushin, obtenu globalement sur M
= R2 avec X(x,y) =
(1,0) et Y (x,y) =
(0,x). (Cf. [25, 37, 57, 62].) D'autres structures presque
riemanniennes ont été obtenues dans des problèmes de
contrôle quantique avec M =
S2 ([35, 36]) et pour d'autres surfaces de
révolution ([33]).
Une structure presque riemannienne sur une surface
s'écrit localement à l'aide d'une des formes normales
suivantes.
Théorème 4.1
Génériquement par rapport à f,
pour tout point q ? M, il existe une base
orthonormale (X, Y ) pour S
sur un voisinage de q et un système de
coordonnées locales tels que (q, X, Y ) admet
l'une des représentations suivantes :
(F1) q = (0,0),
X(x, y) = (1,0), Y
(x, y) = (0,
eö(x,y)),
(F2) q = (0,0),
X(x, y) = (1, 0), Y
(x, y) = (0,
xeö(x,y)),
(F3) q = (0,0),
X(x, y) = (1,0), Y
(x, y) = (0, (y -
x2ø(x))eî(x,y)),
avec ö, ø et
î lisses et
ö(0,y) = 0,
ø(0) =6 0.
Nous disons dans la suite qu'une structure presque
riemannienne S vérifie l'hypothèse
(H0) si elle peut se mettre localement en chaque point sous
l'une des formes normales présentées dans le
théorème 4.1. On dit que une structure presque
riemannienne S vérifiant l'hypothèse
(H0) n'a pas de points de tangence si elle peut
s'écrire localement sous la forme (F1) ou (F2) seulement. Un point
de tangence est, par définition, un point pour lequel
S est décrite localement par (F3).
Soit M compacte, orientée et munie
d'une structure presque riemannienne orientable. Soit K
: M \ Z ? R la courbure gaussienne définie par la
structure presque riemannienne et dAs le
pushforward par f d'une forme de volume sur
E.
Notons Må = {q ? M |
d(q, Z) > å}. Soit
M+ (respectivement, M--) le
sous-ensemble de M \Z sur lequel l'orientation définie
par dAs coïncide avec (respectivement, est
opposée à) celle de M.
Nous pouvons démontrer le résultat suivant, qui
généralise la formule de Gauss-Bonnet. (D'autres
généralisations dans des domaines proches ont été
obtenues pour des structures sousriemanniennes [4], finsleriennes [17] et pour
des pseudo-métriques singulières [92].)
Théorème 4.2
Soit M compacte et orientée. Pour une
structure presque riemannienne orientée, sans points de tangence et
vérifiant l'hypothèse (H0), la limite
limå\0 f Må
K(q)dAs existe et est
égale à
2ð(÷(M+)
- ÷(M--)), oft
÷ est la caractéristique d'Euler.
Étant donné un fibré vectoriel
orienté E de rang deux sur une variété
différentielle compacte orientée M de dimension
deux, le numéro d'Euler de E, noté
par e(E), est défini par
e(E) = E
i(p, ó),
p | ó(p)=0
oil ó : M ? E est une
section transverse à la section nulle et i(p,
ó) = 1 (respectivement, -1) si
dpó : TpM ?
Tó(p)E préserve
(respectivement, reverse) l'orientation.
Remarquons que, en changeant l'orientation sur
M ou sur E, le signe de
e(E) change. Par conséquent,
e(E) est défini au signe près. Par
contre, le numéro d'Euler de TM est défini sans
ambiguïté et est égal à
÷(M). Remarquons aussi que si (E,
f) est trivialisable, alors
e(E) = 0.
Nous avons la caractérisation topologique suivante.
Théorème 4.3
Soit M compacte et orientée dotée d'une
structure presque riemannienne orientée et vérifiant
l'hypothèse (H0). Alors
÷(M+) -
÷(M--) + ô
= e(E), oft
ô est le nombre de révolutions de A
sur Z calculé par rapport à
l'orientation induite par M+
sur Z.
Comme conséquence directe des théorèmes
4.2 et 4.3, nous avons que, pour une structure presque
riemannienne
trivialisable, sans points de tangence, et vérifiant l'hypothèse
(H0), définie sur une
surface M
compacte et orientable, la limite limå\0 f
Må
K(q)dAs existe et est
égale à zéro. Nous
pouvons donner l'interprétation suivante de cette
propriété : pour une structure riemannienne, la topologie de la
surface donne une contrainte sur la courbure totale (formule de Gauss-Bonnet) ;
dans le cas d'une structure presque riemannienne trivialisable, par contre, la
courbure totale est égale à zéro et la topologie de la
surface force la métrique à devenir singulière sur un
ensemble de topologie appropriée.
Il est intéressant de remarquer que toute surface
orientable compacte peut être équipée d'une structure
presque riemannienne trivialisable, sans points de tangence et vérifiant
l'hypothèse (H0) (voir figures 4.1 et 4.2).
X
X
X
X
Y
Y
Y
Y
X
Y
courbes intégrales de X
courbes intégrales de Y
FIGURE 4.1 --- Exemple de structure presque riemannienne
trivialisable sans points de tangence sur une sphère.
Pour étendre le théorème 4.2 au cas des
variétés à bord, nous introduisons une notion de domaine
admissible de M.
Définition 4.4 Soit
U un domaine borné d'une surface
M munie d'une structure presque riemannienne orientable et
vérifiant l'hypothèse (H0). Nous disons
que U est admissible si
U ne contient pas de points de tangence et si le
bord de U est l'union des supports d'un
ensemble fini de courbes ã1, .
. . ,ãm telles que chaque
ãl : [0, Tl]
M satisfait les conditions suivantes :
ãl est C2
sur [0, Tl] ;
ãl est localement solution de (4.1) (en
particulier a longueur finie) ;
ãl a la même orientation que celle induite
sur par U.
Théorème 4.5
Soit U un domaine admissible d'une
surface M munie d'une structure
presque
riemannienne orientable et vérifiant l'hypothèse
(H0). Soient
ã1, . . . ,
ãm comme dans la défini-
tion
4.4. Pour tout å > 0, soit
M#177;å = M#177; fl
Må et
U#177;å =
M#177;å fl U. Soient
tj1, . . . ,
tjlj les temps
pour lesquels ãj
traverse i. Associons à chaque
tjl la quantité
Ó+(tjl ) de la
façon suivante : si,
pour å > 0
suffisamment petit, le support de ãj|(tj l
,tj l +å) est contenu
dans M+, alors
Ó+(tjl ) =
1,
sinon
Ó+(tjl) =
--1. De façon similaire, si pour å
> 0 suffisamment petit le support de
ãj|(tjl
-å,tjl )
est contenu dans M+
alors posons
Ó-(tjl ) =
1, sinon
Ó-(tjl )
= --1. Notons par
kjg(t) la courbure
géodésique de ãj en
ãj(t). Définissons
Î
Õ(Î) =2V 1
--
Î2 + arccos(Î) 41
|
|
X=
Y=
|
A
|
|
|
|
|
|
|
X
de Y
|
|
|
|
|
|
|
|
|
|
zéros de
zéros
|
|
|
|
|
B lieu singulier
|
FIGURE 4.2 --- Exemple de structure presque riemannienne
trivialisable sans points de tangence sur la somme connexe de plusieurs
tores.
et
|
Î#177;(tjl
) = lim
t?tj l #177;
|
kj g(t)|t -
tj l |,á(tjl ) =
Ó-(tjl
)Õ(Î-(tjl
)) + Ó+(tjl
)Õ(Î+(tjl
)).
|
Alors
m
lim KdAs+ k
do-
g kgdo-) =
271-(x(U+)
-- x(U))--
á(tjl),
å?0
(fk?U,
frn?Uk frn?U
j=1 l=1
oft nous interprétons chaque
intégrale fn?U#177;
å kgdó comme la somme des
intégrales le long des portions lisses de n
?U#177;å plus la somme des angles aux
points oft n'est pas C1.
Si, de plus, est
C2 dans un voisinage de Z,
alors
ZU
oft
KdAs + f kgdós
=
2ð(÷(U+)
- ÷(U)),
aU
ZU
KdAs = lim
KdAs,
å?0
fukå?U-å
|
kgdós =
faU å?0 (f
rn?Uk å
|
k dó -
k dó) .
frn?U
|
Le théorème 4.5 peut être utilisé
pour démontrer une version du théorème 4.2 dans laquelle
les points de tangence sont admis. L'idée est que, contrairement
à ce qui arrive aux points de type (F2), près des points de
tangence, le bord de Må converge vers
Z, pour å ? 0, avec un taux de convergence
différent de å (par rapport à un
système de coordonnées quelconque). Nous devons
U
Z
FIGURE 4.3 - Un domaine admissible U.
alors isoler les points de tangence grâce au calcul de
l'intégrale de K sur une région qui
dépend de plusieurs paramètres qui convergent vers zéro
sur différentes échelles de temps. Plus
précisément, soit T l'ensemble des point de
tangence de la structure presque riemannienne. Associons à tout
q ? T un voisinage « rectangulaire » Bq
ä1,ä2 dépendant de deux
paramètres ä1 et ä2, qui
jouent le rôle des longueurs des cotés du rectangle, avec la
construction suivante : considérons une courbe lisse
(-1, 1) ? s 7?
w(s) qui passe par le point de tangence
w(0) = q et qui est transverse à z en
q ; pour tout s ?
(-1, 1), soit
ãs la géodésique
paramétrée par son abscisse curviligne telle que
ãs(0) =
w(s) et qui minimise localement la distance
à {w(s) | s ?
(-1, 1)}
(ãs est bien définie en
raison de la transversalité de w); pour
ä1 et ä2 suffisamment petits, le
rectangle Bq ä1,ä2 est le
sous-ensemble de M qui contient le point q et
dont le bord est
ãä2([-ä1,
ä1]) ?
ã[-ä2,ä2](ä1)
? ã-ä2([-ä1,
ä1]) ?
ã[-ä2,ä2](-ä1)
(voir figure 4.4).
Soit Må ä1,ä2 =
Må \ Uq?T Bq
ä1,ä2. Nous pouvons démontrer le
résultat suivant, qui généralise le théorème
4.2 et, par conséquent, la formule de Gauss-Bonnet.
Théorème 4.6 Soit
M compacte et orientée. Pour une structure
presque riemannienne orientée qui vérifie l'hypothèse
(H0), la limite
f
uim uim uim
K(q)dAs (4.2)
ä1?0
ä2?0 å?0
Må
ä1,ä2
existe et est égale à
2ð(÷(M+)
- ÷(M-) + ô) =
2ðe(E). En particulier, la limite
vaut zéro si et seulement si la structure est trivialisable.
Remarquons que la construction de Må
ä1,ä2 dépend du choix des courbes
w transverses à z aux points de T et
de leur paramétrage. Le théorème 4.6 affirme que la valeur
de la limite (4.2) est, néanmoins, intrinsèque.
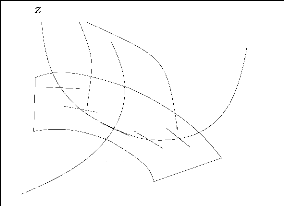
ãä2(-ä1)
ã-ä2(-ä1)
A
w(-ä2)
q
w(ä2)
ã-ä2(ä1)
M+
ãä2(ä1)
M-
FIGURE 4.4 -- La construction de
Bq
ä1,ä2.
Nous terminons ce chapitre avec l'analyse de ce qui arrive si
l'on essaye de calculer (4.2) en remplaçant
Måä1,ä2 par
Må, en analogie avec l'enonce du theorème
4.2.
D'abord, grâce à la formule de Gauss-Bonnet
riemannienne et en supposant que å est
petit,
K(q)dA5
=
2ð(÷(ME+)
- ÷(ME)) - f
kgds + f kgds
Lå aW f å
=
2ð(÷(M+)
- ÷(M-)) - f kgds
+ f kgds
aMå + aM;
où nos avons utilise la notation
M#177;å = M#177; n
Må. Il n'est pas difficile de verifier, en utilisant
la forme normale (F2), que les contributions des courbures geodesiques
de ?M+å
et ?M-å s'annulent reciproquement loin des
points de tangence quand å tend vers zero. Nous allons
donc argumenter que la presence de points de tangence peut conduire à la
divergence de limå?0 fMå
K(q)dAs, en calculant
numeriquement la courbure geodesique de
?M+å et
?M-å dans un voisinage d'un tel point. Nous prenons
donc la forme normale (F3) avec ø = 1 et
î = 0, pour laquelle K est donne
explicitement par la formule
K=
-2
(3x2 + y)
(x2 - y)2
.
Le graphe de K est represente en figure 4.5.
Remarquons que lim
supq?(0,0)
K(q) = +8 et lim
infq?(0,0)
K(q) = -8. La situation est
differente de celle que l'on retrouve autour des points ayant pour forme
normale (F2), pour lesquels K(q) diverge
à -8 quand q approche
Z.
Le comportement de ?Må est
illustre en figure 4.6.
Fixons 0 < a < 1 et considerons la
geodesique passant par (a, a2) qui minimise
(localement) la distance à Z. Notons par
P+ et P- les deux points le long de cette
geodesique à distance å de
Z et par ã+ et
ã- les portions de
?M+å et
?M-å joignant l'axe vertical avec les deux points
P+ et P- (voir figure 4.7). La
figure 4.8 montre la valeur de
å (f Kgds - f
Kgds)
7+ f
pour a = 0.1 et
å variant dans l'intervalle
[0.01, 0.04] (calcule
à l'aide du logiciel Mathematica).
FIGURE 4.5 - Graphe de K pour Ä =
span((1, 0), (0, y -
x2))
-1.0 -0.5
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.5 1.0
FIGURE 4.6 - Bord de Må avec
å = 1 2.
La fonction paraît converger vers une valeur finie non
nulle quand å tend à zéro, permettant
ainsi de conjecturer que fMå
K(q)dAs diverge.



Ì
Ì+
å
å
P
Ù+
+
ã
ã
a
Ù
-a
a
2
a
-2.07
-2.08
FIGURE 4.7 - Construction de
ã+ et ã-


-2.04




-2.05

-2.06


0.010 0.015 0.020 0.025 0.030 0.035 0.040
(f )
ã+ Kgds -
f
FIGURE 4.8 Graphe de å
ã- Kgdspour a
= 0.1
Perspectives de recherche
De nombreux sujets de recherche sont laissés ouverts
par les activités présentées dans les quatre chapitres
précédents. Certains de ces sujets sont déjà en
cours avancé de développement, d'autres font l'objet
d'activités de recherche programmées dans un futur proche,
d'autres encore à plus long terme.
Concernant les activités présentées dans
le premier chapitre, dédié à la commande des
systèmes non linéaires de dimension finie, le
développement du sujet de la section 1.2 (suivi de trajectoire pour un
sous-marin) a donné lieu à l'encadrement du post-doc de
María Barbero Liñán sur une généralisation
de l'approche backstepping à une classe beaucoup plus vaste de
systèmes mécaniques. Il s'agissait en particulier de faire le
lien entre nos résultats de suivi de trajectoire et ceux
présentés dans [40] dans le cadre abstrait des systèmes de
contrôle dits à connexion affine. Dans un travail en
cours de rédaction, nous avons pu étendre les résultats de
[40] en généralisant au cadre de la connexion affine l'approche
utilisé dans [MS.7] pour étudier le suivi de trajectoire d'un
sous-marin. Nous avons aussi rendu la construction plus algorithmique, en
étudiant comment les pas successifs de la procédure par
backstepping doivent être hiérarchisés. Plus
précisément, nous avons analysé les rapports quantitatifs
entre les paramètres correspondant aux différents pas,
aboutissant ainsi à des familles de lois de commande, dépendant
d'un seul paramètre, qui réalisent le suivi de trajectoire
désiré.
Des perspectives de développement de ce sujet qui
m'intéressent beaucoup sont celles liées à l'analyse de
complexité des commandes obtenues par les algorithmes de suivi de
trajectoire. Il s'agit en général de lois de commande qui
oscillent fortement. Pour pouvoir obtenir des bonnes performances sur des
modèles réels, il faut minimiser la fréquence des
oscillations des lois de commande en préservant la même
tolérance par rapport à la trajectoire cible.
Dans la même thématique des systèmes non
linéaires de dimension finie, je suis en train de collaborer avec
François Alouges et Karine Beauchard sur un problème d'inversion
de la magnétisation de micro-aimants ellipsoïdaux ayant des
applications dans le développement de systèmes de stockage de
type MRAM. La magnétisation m à
l'intérieur du corps ferromagnétique Ù c
R est un champs de vecteurs de norme constante, régi par
l'équation de Landau-Lifschitz
?m ?t =
á(H(m) --
(H(m),m)m) -- m A
H(m), x E
Ù,
oil H(m) indique le champs
magnétique total. Nous nous intéressons à la planification
des trajectoires pour des réductions de dimension finie de ce
modèle.
Le thème qui sera probablement au centre de mes
activités de recherche dans les prochaines années est celui issu
des travaux sur le contrôle quantique présentés dans le
chapitre 2. Il s'agit d'abord d'améliorer les résultats
déjà obtenus en relaxant les hypothèses suffisantes de
contrôlabilité approchée de l'équation de
Schrödinger bilinéaire présentées en section 2.1. Si
notre intuition concernant les hypothèses minimales qui garantissent la
contrôlabilité approchée est correcte, il sera alors
possible d'utiliser la construction à la base de notre preuve
d'existence pour déterminer des algorithmes explicites de planification
de trajectoires. En collaboration avec des physiciens expérimentaux de
Dijon (en particulier Dominique Sugny) nous voulons alors tester
nos algorithmes sur des problèmes d'orientation et
alignement de molécules. Ces problèmes méritent
d'être aussi étudiés ultérieurement du point de vue
théorique, en étendant les résultats que nous avons
obtenus pour les rotations sur un cercle d'une molécule linéaire
rigide. Dans ce contexte, le prochain cas à considérer est, sans
doute, celui des rotations sur une sphère de R3.
En collaboration avec Ugo Boscain, Thomas Chambrion et Paolo
Mason nous voudrions aussi transférer, si possible, les résultats
que nous avons obtenu pour le contrôle des matrices de densité au
cas où le spectre de l'opérateur n'est pas discret, en
étudiant, en particulier, l'évolution dans l'espace
engendré par les états propres qui correspondent à la
partie discrète du spectre. Nous pourrions alors compléter les
résultats de commandabilité approchée obtenus par
Mirraihimi dans ce contexte dans (cf. [82]).
Nous voudrions aussi nous pencher sur les modèles
quantiques non linéaires, en commençant par l'équation de
Gross-Pitaevski. Il ne nous parait pas impossible d'adapter un cas non
linéaire la partie finie dimensionnelle des arguments à la base
de nos résultats de commandabilité approchée. Une
contrainte importante pour l'application complète de notre
méthode nous semble plutôt physique, à savoir le domaine de
validité de l'équation de Gross-Pitaevski, qu'il ne faut bien
sûr pas forcer au delà de ses limites.
Un autre sujet très intéressant est celui de la
commande adiabatique des systèmes quantiques (cf. [112]). L'objectif
dans ce domaine est de développer dans un cadre mathématique
général les techniques de commande proposées par les
physiciens et étudiées du point de vue du contrôle, dans
des situations spécifiques, par Adami et Boscain dans [1]. On vise ici
des équations de Schrödinger avec au moins deux contrôles
scalaires qui varient très lentement. Un des outils importants pour
estimer l'évolution de ces systèmes est l'analyse de comment le
spectre d'un opérateur de Schrödinger perd sa simplicité et
de son développement paramétrique autour d'un point de non
simplicité. On sait donner à l'ensemble des potentiels
correspondants à des opérateurs de Schrödinger ayant spectre
non simple une structure différentielle (cf. [48, 71, 76]). Il faudra
alors utiliser des arguments de transversalité pour garantir,
génériquement, l'applicabilité des méthodes
adiabatiques. Pour cette raison, cette thématique de recherche rejoint
celle des sections 2.3 et 2.4.
En restant dans le domaine du contrôle des
systèmes quantiques, je voudrais aussi m'intéresser à la
question de la description des obstructions à la commandabilité
exacte de l'équation de Schrödinger. Les travaux de Beauchard [22]
et Beauchard et Coron [24] ont donné une description assez
précise de l'ensemble atteignable d'une équation de
Schrödinger particulière. Il est remarquable que les états
propres de l'opérateur non contrôlé sont exactement
joignables par des trajectoires admissibles pour une large classe
d'opérateurs de contrôle (cf. [23]). Cela donne l'espoir qu'il
soit possible d'isoler des propriétés générales des
ensembles atteignables des systèmes quantiques.
Concernant le chapitre 3, dédié à la
stabilité des systèmes hybrides, je voudrais d'abord poursuivre
les collaborations déjà entamées avec Pierre Riedinger,
Jamal Daafouz, Ulysse Serres et Jean-Claude Vivalda sur la commande des
convertisseurs de puissance multicellulaires. Ce sont des systèmes
électriques qui peuvent atteindre des puissances de quelques
mégawatts et emploient généralement des tensions de
plusieurs kilovolts. Ces systèmes sont particulièrement
intéressants pour des applications de forte puissance avec des hautes
tensions (cf. [79]). L'objectif est de proposer des solutions originales et
intrinsèquement hybrides dans le cadre de l'amélioration des
performances dynamiques de cette classe de systèmes ainsi que la
diminution du nombre de capteurs nécessaires.
J'envisage aussi de développer ma recherche sur les
systèmes linéaires à commutations en temps discret,
présentée en section 3.3. Dans ce contexte, en collaboration avec
Jamal Daafouz, un premier objectif est de caractériser les lois de
commutation ne permettant pas de converger vers l'origine et la structure des
ensembles limites. Cette caractérisation pourrait ensuite être
ex-
ploitée pour l'analyse d'observabilité et la
synthèse d'observateurs des systèmes à commutations en
temps discret. L'extension des résultats de stabilité au cas non
linéaire planaire est également envisagée. D'autres
extensions possibles des résultats de la section 3.3 concernent des
contraintes de type lipschitz que l'on peut ajouter à la variation des
paramètres de commutation, ou bien des dépendances plus
élaborées de la fonction de Liapounov par rapport à
l'évolution passée de ces mêmes paramètres.
Un autre thème de recherche que je souhaite
développer en collaboration avec Yacine Chitour et Paolo Mason dans le
cadre des systèmes dynamiques hybrides est celui de la
caractérisation de l'instabilité maximale d'un système
linéaire à commutations à temps continu. Cette
caractérisation passe à la fois par la description des
systèmes à commutations dont l'instabilité est polynomiale
et par la recherche des trajectoires périodiques des systèmes
marginalement stables (cf. [18, 19, 77]).
Une autre activité de recherche en cours de lancement,
en collaboration avec Martin Gugat, concerne l'analyse de stabilité de
systèmes de contrôle de dimension infinie modélisant des
réseaux de cordes (cf. [51]). L'idée est de développer une
approche similaire à celle présentée en section 3.2. Le
passage à la dimension infinie donne naissance à des nouveaux
phénomènes d'instabilité, comme il a été
remarqué dans [63].
Relativement au quatrième axe, l'étude de la
géométrie presque riemannienne présentée dans le
chapitre 4, nous sommes en train d'établir, en collaboration avec Ugo
Boscain, Grégoire Char-lot et Roberta Ghezzi, une caractérisation
complète des classes d'équivalence des structures presque
riemanniennes en dimension deux, où l'équivalence est
considérée par rapport à l'existence de transformations
bi-lipschitiennes. Cette caractérisation se fait en associant à
chaque structure presque riemannienne un graphe libellé qui contient
tous ses invariants. Nous étudions aussi la construction d'une forme
normale intrinsèque autour d'un point de tangence. En reprenant la
démonstration du théorème 4.1, on s'aperçoit que
cela revient à construire de façon intrinsèque une courbe
paramétrée, transverse à l'ensemble singulier au point de
tangence.
Bibliographie
[1] Riccardo ADAMi et Ugo BoSCAiN : Controllability of the
Schrödinger equation via intersection of eigenvalues. In Proceedings
of the 44th IEEE Conference on Decision and Control, pages 1080-1085,
2005.
[2] Shmuel AGMoN : Bounds on exponential decay of
eigenfunctions of Schrödinger operators. In Schrödinger operators
(Como, 1984), volume 1159 de Lecture Notes in Math., pages 1- 38.
Springer, Berlin, 1985.
[3] Andrei AGRACHEv et Thomas CHAMBRioN : An estimation of
the controllability time for single-input systems on compact Lie groups.
ESAIM Control Optim. Calc. Var., 12(3):409- 441, 2006.
[4] Andrei A. AGRACHEv : A «Gauss-Bonnet formula» for
contact sub-Riemannian manifolds. Dokl. Akad. Nauk, 381(5):583-585,
2001.
[5] Andrei A. AGRACHEv et Daniel LiBERzoN : Lie-algebraic
stability criteria for switched systems. SIAM J. Control Optim.,
40(1):253-269, 2001.
[6] Andrei A. AGRACHEv et Yuri L. SACHKov : Control
theory from the geometric viewpoint, volume 87 de Encyclopaedia of
Mathematical Sciences. Springer-Verlag, Berlin, 2004. Control Theory and
Optimization, II.
[7] Andrey A. AGRACHEv et Andrey V. SARyCHEv : Controllability
of 2D Euler and NavierStokes equations by degenerate forcing. Comm. Math.
Phys., 265(3):673-697, 2006.
[8] Jeffrey H. ALBERT : Genericity of simple eigenvalues for
elliptic PDE's. Proc. Amer. Math. Soc., 48:413-418, 1975.
[9] Francesca ALBERTiNi et Domenico D'ALESSANDRo : Notions of
controllability for bilinear multilevel quantum systems. IEEE Trans.
Automat. Control, 48(8):1399-1403, 2003.
[10] François ALouGES, Antonio DESiMoNE et Aline LEFEBvRE
: Optimal strokes for low Reynolds number swimmers : an example. J.
Nonlinear Sci., 18(3):277-302, 2008.
[11] Claudio ALTAFiNi : Controllability properties for finite
dimensional quantum Markovian master equations. J. Math. Phys.,
44(6):23572372, 2003.
[12] B. D. O. ANDERSoN, R. R. BiTMEAD, C. R. JoHNSoN, P. V.
KoKoToviC, R. L. KoSuT, I. M. Y. MAREELS, L. PRALy et B. D. RiEDLE :
Stability of adaptive systems : Passivity and averaging analysis. MIT
Press, 1986.
[13] A. ASToLFi, D. CHHABRA et R. ORTEGA : Asymptotic
stabilization of some equilibria of an underactuated underwater vehicle.
Systems Control Lett., 45(3):193206, 2002.
[14] Moussa BALDE et Ugo BoSCAiN : Stability of planar switched
systems : the nondiagonalizable case. Commun. Pure Appl. Anal.,
7(1):121, 2008.
[15] John M. BALL, Jerrold E. MARSDEN et Marshall SLEMRoD :
Controllability for distributed bilinear systems. SIAM J. Control
Optim., 20(4):575597, 1982.
[16] Werner BALLMANN, Mikhael GRoMov et Viktor SCHRoEDER
: Manifolds of nonpositive curvature, volume 61 de Progress in
Mathematics. Birkhäuser Boston Inc., Boston, MA, 1985.
[17] David BAo, Shiing-Shen CHERN et Zhongmin SHEN : An
introduction to Riemann-Finsler geometry, volume 200 de Graduate Texts
in Mathematics. Springer-Verlag, New York, 2000.
[18] Nikita E. BARABANov : An absolute characteristic exponent
of a class of linear nonstationary systems of differential equations.
Sibirsk. Mat. Zh., 29(4):12-22, 222, 1988.
[19] Nikita E. BARABANov : Asymptotic behavior of extremal
solutions and structure of extremal norms of linear differential inclusions of
order three. Linear Algebra Appl., 428(10):2357-2367, 2008.
[20] B. Ross BARMiSH : Stabilization of uncertain systems via
linear control. IEEE Trans. Automat. Contr., 28(8):848-850, 1983.
[21] K. BEAuCHARD, Y. CHiTouR, D. KATES et R. LoNG : Spectral
controllability for 2D and 3D linear Schrödinger equations. J. Funct.
Anal., 256(12):3916-3976, 2009.
[22] Karine BEAuCHARD : Local controllability of a 1-D
Schrödinger equation. J. Math. Pures Appl. (9), 84(7):851-956,
2005.
[23] Karine BEAuCHARD : Control of Schrödinger
equations. Notes du Cours Peccot, Collège de France, 2007.
[24] Karine BEAuCHARD et Jean-Michel CoRoN : Controllability of
a quantum particle in a moving potential well. J. Funct. Anal.,
232(2):328-389, 2006.
[25] André BELLAICHE : The tangent space in
sub-Riemannian geometry. In Sub-Riemannian geometry, volume 144 de
Progr. Math., pages 1-78. Birkhäuser, Basel, 1996.
[26] H. C. BERG et R. ANDERSoN : Bacteria swim by rotating their
flagellar filaments. Nature, 245:380-382, 1973.
[27] J. BLAKE : A finite model for ciliated micro-organisms.
J. Biomech., 6:133-140, 1973.
[28] Franco BLANCHiNi et Stefano MiANi : Stabilization of LPV
systems : state feedback, state estimation, and duality. SIAM J. Control
Optim., 42(1):76-97, 2003.
[29] Anthony M. BLoCH, Roger W. BRoCKETT et Chitra RANGAN : The
controllability of infinite quantum systems and closed subspace criteria.
Preprint, 2006.
[30] Anthony M. BLoCH, Perinkulam Sambamurthy KRiSHNApRASAD,
Jerrold E. MARSDEN et Gloria Sánchez de ALvAREz : Stabilization of rigid
body dynamics by internal and external torques. Automatica J. IFAC,
28(4):745-756, 1992.
[31] Anthony M. BLoCH, Naomi Ehrich LEoNARD et Jerrold E.
MARSDEN : Stabilization of mechanical systems using controlled Lagrangians.
In Proceedings of the 36th IEEE Conference on Decision and Control, pages
2356-2361, 1997.
[32] Vincent D. BLoNDEL et Yurii NESTERov : Computationally
efficient approximations of the joint spectral radius. SIAM J. Matrix Anal.
Appl., 27(1):256272, 2005.
[33] Bernard BoNNARD, Jean-Baptiste CAiLLAu, Robert SiNCLAiR
et Minoru TANAKA : Conjugate and cut loci of a two-sphere of revolution with
application to optimal control. Ann. Inst. H. Poincaré Anal. Non
Linéaire, 26(4):10811098, 2009.
[34] Ugo BoSCAiN : Stability of planar switched systems : the
linear single input case. SIAM J. Control Optim., 41(1):89112,
2002.
[35] Ugo BoSCAiN, Thomas CHAMBRioN et Grégoire CHARLoT
: Nonisotropic 3-level quantum systems : complete solutions for minimum time
and minimum energy. Discrete Contin. Dyn. Syst. Ser. B, 5(4):957990,
2005.
[36] Ugo BoScAiN, Grégoire CHARLoT, Jean-Paul
GAuTHiER, Stéphane GuERiN et Hans-Rudolf JAuSLiN : Optimal control in
laser-induced population transfer for two- and three-level quantum systems.
J. Math. Phys., 43(5):2107-2132, 2002.
[37] Ugo BoScAiN et Benedetto PiccoLi : A short introduction to
optimal control. In T. SARi, éditeur : Contrôle Non
Linéaire et Applications, pages 19-66. Hermann, Paris, 2005.
[38] Stephen BoyD, Laurent EL GHAoui, Eric FERoN et
Venkataramanan BALAKRiSHNAN : Linear matrix inequalities in system and
control theory, volume 15 de SIAM Studies in Applied Mathematics.
Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA,
1994.
[39] C. BRENNEN : An oscil lating-boundary-layer theory for
ciliary propulsion. J. Fluid Mech., 65:799-824, 1974.
[40] Francesco BuLLo et Andrew D. LEwiS : Geometric
control of mechanical systems, volume 49 de Texts in Applied
Mathematics. Springer-Verlag, New York, 2005. Modeling, analysis, and
design for simple mechanical control systems.
[41] Mark S. ByRD et Navin KHANEjA : Characterization of the
positivity of the density matrix in terms of the coherence vector
representation. Phys. Rev. A (3), 68(6):062322, 13, 2003.
[42] Thomas CHAMBRioN : Approximate tracking for a system of
Schrödinger equations. Preprint, 2009.
[43] Stephen CHiLDRESS : Mechanics of swimming and
flying, volume 2 de Cambridge Studies in Mathematical Biology.
Cambridge University Press, Cambridge, 1981.
[44] Yacine CHiTouR : Applied and theoretical aspects of the
controllability of nonholonomic control system. PhD Thesis, Rutgers
University, 1996.
[45] Yacine CHiTouR, Jean-Michel CoRoN et Mauro GARAVELLo :
On conditions that prevent steady-state controllability of certain linear
partial differential equations. Discrete Contin. Dyn. Syst.,
14(4):643-672, 2006.
[46] Monique CHyBA, Naomi Ehrich LEoNARD et Eduardo D. SoNTAG
: Singular trajectories in multi-input time-optimal problems : application to
controlled mechanical systems. J. Dynam. Control Systems,
9(1):103-129, 2003.
[47] Monique CHyBA, Helmut MAuRER, Héctor J. SuSSMANN
et Vossen GoTTFRiED : Underwater vehicles : The minimum time problem. In
Proceedings of the 43th IEEE Conference on Decision and Control, pages
1370-1375, 2004.
[48] Yves Colin de VERDiERE : Sur une hypothèse de
transversalité d'Arnol'd. Comment. Math.
Helv., 63(2):184-193, 1988.
[49] Jean-Michel CoRoN : Control and nonlinearity,
volume 136 de Mathematical Surveys and Monographs. American
Mathematical Society, Providence, RI, 2007.
[50] Jamal DAAFouZ et Jacques BERNuSSou : Parameter dependent
Lyapunov functions for discrete time systems with time varying parametric
uncertainties. Systems Control Lett., 43(5):355359, 2001.
[51] René DAGER et Enrique ZuAZuA : Wave
propagation, observation and control in 1-d
flexible multi-structures, volume 50 de Mathématiques 6
Applications (Berlin) [Mathematics 6 Applications]. Springer-Verlag,
Berlin, 2006.
[52] Domenico D'ALESSANDRo : Introduction to quantum
control and dynamics. Applied Mathematics and Nonlinear Science Series.
Boca Raton, FL : Chapman, Hall/CRC., 2008.
[53] Wijesuriya P. DAyAwANsA et C. F. MARTiN : A converse
Lyapunov theorem for a class of dynamical systems which undergo switching.
IEEE Trans. Automat. Control, 44(4):751- 760, 1999.
[54] Lester E. DuBiNs : On curves of minimal length with a
constraint on average curvature, and with prescribed initial and terminal
positions and tangents. Amer. J. Math., 79:497- 516, 1957.
[55] Sylvain ERVEDozA et Jean-Pierre PuEL : Approximate
controllability for a system of Schrödinger equations modeling a single
trapped ion. Ann. Inst. H. Poincaré Anal. Non Linéaire,
26:2111-2136, 2009.
[56] Eric FERoN, Pierre APKARiAN et Pascal GAHiNET : Analysis
and synthesis of robust control systems via parameter-dependent Lyapunov
functions. IEEE Trans. Automat. Control, 41(7):1041-1046, 1996.
[57] Bruno FRANCHi et Ermanno LANCoNELLi : Une
métrique associée à une classe d'opérateurs
elliptiques dégénérés. Rend. Sem. Mat. Univ.
Politec. Torino, (Special Issue):105-114 (1984), 1983. Conference on
linear partial and pseudodifferential operators (Torino, 1982).
[58] D. FRENKEL et R. PoRTuGAL : Algebraic methods to compute
Mathieu functions. J. Phys. A, 34(17):3541-3551, 2001.
[59] Giovanni P. GALDi : An introduction to the
mathematical theory of the Navier-Stokes equations. Vol. I, volume 38
de Springer Tracts in Natural Philosophy. Springer-Verlag, New York,
1994. Linearized steady problems.
[60] Jean-Paul GAuTHiER et Ivan A. K. KuPKA : Observability and
observers for nonlinear systems. SIAM J. Control Optim.,
32(4):975-994, 1994.
[61] José C. GERoMEL et Patrizio CoLANERi : Robust
stability of time varying polytopic systems. Systems Control Lett.,
55(1):81-85, 2006.
[62] V. V. GRuS'iN : A certain class of hypoelliptic
operators. Mat. Sb. (N.S.), 83 (125):456-473, 1970.
[63] Alain HARAuX, Patrick MARTiNEz et Judith VANCosTENoBLE :
Asymptotic stability for intermittently controlled second-order evolution
equations. SIAM J. Control Optim., 43(6):2089-2108, 2005.
[64] Pascal HEBRARD et Antoine HENRoT : Optimal shape and
position of the actuators for the stabilization of a string. Systems
Control Lett., 48(3-4):199-209, 2003. Optimization and control of
distributed systems.
[65] Dan HENRy : Perturbation of the boundary in
boundary-value problems of partial differential equations, volume 318
de London Mathematical Society Lecture Note Series. Cambridge
University Press, Cambridge, 2005. With editorial assistance from Jack Hale and
Antônio Luiz Pereira.
[66] Luc HiLLAiRET et Chris JuDGE : Generic spectral simplicity
of polygons. Proc. Amer. Math. Soc., 137(6):21392145, 2009.
[67] Patrick HCHLER, Joachim BARGoN et Steffen J GLAsER :
Nuclear magnetic resonance quantum computing exploiting the pure spin state of
para hydrogen. J. Chem. Phys., 113(6):20562059, 2000.
[68] Velimir JuRDjEViC : Geometric control theory,
volume 52 de Cambridge Studies in Advanced Mathematics. Cambridge
University Press, Cambridge, 1997.
[69] Tosio KATo : Perturbation theory for linear
operators. Die Grundlehren der mathematischen Wissenschaften, Band 132.
Springer-Verlag New York, Inc., New York, 1966.
[70] Horace LAMB : Hydrodynamics. Cambridge
Mathematical Library. Cambridge University Press, Cambridge, sixth
édition, 1993. With a foreword by R. A. Caflisch [Russel E.
Caflisch].
[71] Pier Domenico LAMBERTi et Massimo LANZA DE CRisToFoRis :
Persistence of eigenvalues and multiplicity in the Dirichlet problem for the
Laplace operator on nonsmooth domains. Math. Phys. Anal. Geom.,
9(1):65-94, 2006.
[72] Naomi Ehrich LEoNARD : Mechanics and nonlinear control :
Making underwater vehicles ride and glide. In Proc. 4th IFAC Nonlinear
Control Design Symp., pages 1-6, 1998.
[73] Daniel LiBERZoN : Switching in systems and
control. Systems & Control : Foundations & Applications.
Birkhäuser Boston Inc., Boston, MA, 2003.
[74] James LiGHTHiLL : Mathematical
biofluiddynamics. Society for Industrial and Applied Mathematics,
Philadelphia, Pa., 1975. Based on the lecture course delivered to the
Mathematical Biofluiddynamics Research Conference of the National Science
Foundation held from July 16-20, 1973, at Rensselaer Polytechnic Institute,
Troy, New York, Regional Conference Series in Applied Mathematics, No. 17.
[75] Jacques-Louis LioNs et Enrique ZuAZuA : A generic
uniqueness result for the Stokes system and its control theoretical
consequences. In Partial differential equations and applications,
volume 177 de Lecture Notes in Pure and Appl. Math., pages 221-235.
Dekker, New York, 1996.
[76] Daniela Lupo et Anna Maria MiCHELETTi : A remark on the
structure of the set of perturbations which keep fixed the multiplicity of two
eigenvalues. Rev. Mat. Apl., 16(2): 47-56, 1995.
[77] Michael MARGALioT et Christos YFouLis : Absolute stability
of third-order systems : a numerical algorithm. Automatica J. IFAC,
42(10):1705-1711, 2006.
[78] Paolo MAsoN, Ugo BosCAiN et Yacine CHiTouR : Common
polynomial Lyapunov functions for linear switched systems. SIAM journal on
control and optimization, 45:226-245, 2006.
[79] T.A. MEYNARD, H. FoCH, P. THoMAs, J. CouRAuLT, R. JAkoB
et M. NAHRsTAEDT : Multicell converters : basic concepts and industry
applications. IEEE Transactions on Industrial Electronics,
49(5):955-964, 2002.
[80] Anna Maria MiCHELETTi : Perturbazione dello spettro
dell'operatore di Laplace, in relazione ad una variazione del campo. Ann.
Scuola Norm. Sup. Pisa (3), 26:151-169, 1972.
[81] Mazyar MiRRAHiMi : Lyapunov control of a particle in a
finite quantum potential well. In Proceedings of the 45th IEEE Conference
on Decision and Control, 2006.
[82] Mazyar MiRRAHiMi : Lyapunov control of a quantum particle
in a decaying potential. Ann. Inst. H. Poincaré Anal. Non
Linéaire, 26(5):1743-1765, 2009.
[83] Mazyar MiRRAHiMi et Pierre RouCHoN : Controllability of
quantum harmonic oscillators. IEEE Trans. Automat. Control,
49(5):745747, 2004.
[84] Dirk MiTTENHuBER : Dubins' problem in the hyperbolic
plane using the open disc model. In Geometric control and non-holonomic
mechanics (Mexico City, 1996), volume 25 de CMS Conf. Proc.,
pages 115152. Amer. Math. Soc., Providence, RI, 1998.
[85] Dirk MiTTENHuBER : Dubins' problem is intrinsically
three-dimensional. ESAIM Control Optim. Calc. Var., 3:122, 1998.
[86] Felipe MoNRoY-PEREZ : Three-dimensional non-Euclidean
Dubins' problem. In Geometric control and non-holonomic mechanics (Mexico
City, 1996), volume 25 de CMS Conf. Proc., pages 153181. Amer.
Math. Soc., Providence, RI, 1998.
[87] Vahagn NERsEsyAn : Growth of Sobolev norms and
controllability of the Schrödinger equation. Comm. Math. Phys.,
290(1):371-387, 2009.
[88] S. P. Novikov et I.
ShmEL'tsER : Periodic solutions of Kirchhoff
equations for the free motion of a rigid body in a fluid and the extended
Lyusternik-Shnirel'man-Morse theory. I.
Funktsional. Anal. i Prilozhen., 15(3):54-66, 1981.
[89] Jaime H. ORtEgA et Enrique ZuAzuA : Generic simplicity of
the spectrum and stabilization for a plate equation. SIAM J. Control
Optim., 39(5):1585-1614, 2000.
[90] Jaime H. ORtEgA et Enrique ZuAzuA : Generic simplicity of
the eigenvalues of the Stokes system in two space dimensions. Adv.
Differential Equations, 6(8):987-1023, 2001.
[91] A PEiRcE, M DAhLEh et H RAbitz : Optimal control of quantum
mechanical systems: Existence, numerical approximations, and applications.
Phys. Rev. A, 37:4950-4964, 1988.
[92] Fernand PELLEtiER : Sur le théorème de
Gauss-Bonnet pour les pseudo-métriques singulières. In
Séminaire de Théorie Spectrale et Géométrie, No. 5,
Année 1986-1987, pages 99-105. Univ. Grenoble I, Saint, 1987.
[93] V. Yu. PRotAsov : A generalized joint spectral radius. A
geometric approach. Izv. Ross. Akad. Nauk Ser. Mat., 61(5):99-136,
1997.
[94] E. M. PuRcELL : Life at low Raynolds numbers. Am. J.
Phys., 45:3-11, 1977.
[95] H. RAbitz, H. de ViviE-RiEdLE, R. Motzkus et K. KompA :
Wither the future of controlling quantum phenomena? SCIENCE,
288:824-828, 2000.
[96] Rajamani RAvi, Krishan M. NAgpAL et Pramod P.
KhARgonEkAR : H8 control of linear time-varying
systems : a state-space approach. SIAM J. Control Optim.,
29(6):1394-1413, 1991.
[97] Michael REEd et Barry Simon : Methods of modern
mathematical physics. IV. Analysis of operators. Academic Press [Harcourt
Brace Jovanovich Publishers], New York, 1978.
[98] Franz RELLich : Perturbation theory of eigenvalue
problems. Assisted by J. Berkowitz. With a preface by Jacob T. Schwartz.
Gordon and Breach Science Publishers, New York, 1969.
[99] Sérgio S. RodRiguEs : Navier-Stokes equation on the
rectangle controllability by means of low mode forcing. J. Dyn. Control
Syst., 12(4):517-562, 2006.
[100] Pierre Rouchon : Control of a quantum particle in a
moving potential well. In Lagrangian and Hamiltonian methods for nonlinear
control 2003, pages 287-290. IFAC, Laxenburg, 2003.
[101] Jorge SAn MARtín, Takéo TAkAhAshi et Marius
TucsnAk : A control theoretic approach to the swimming of microscopic
organisms. Quart. Appl. Math., 65:405-424, 2007.
[102] T. SEidEmAn et E. HAmiLton : Nonadiabatic alignment by
intense pulses : concepts, theory and directions. Adv. At. Mol. Opt.
Phys., 52:289, 2006.
[103] M. ShApiRo et P. BRumER : Principles of the Quantum
Control of Molecular Processes. Principles of the Quantum Control of
Molecular Processes, pp. 250. Wiley-VCH, février 2003.
[104] Takashi ShioyA : The limit spaces of two-dimensional
manifolds with uniformly bounded integral curvature. Trans. Amer. Math.
Soc., 351(5):17651801, 1999.
[105] M. SpAnnER, E. A. ShApiRo et M. IvAnov : Coherent control
of rotational wave-packet dynamics via fractional revivals. Phys. Rev.
Lett., 92:093001, 2004.
[106] Michael SpivAk : A comprehensive introduction to
differential geometry. Vol. II. Publish or Perish Inc., Wilmington, Del.,
second édition, 1979.
[107] H. STApELFELDT et T. SEiDEMAN : Aligning molecules with
strong laser pulses. Rev. Mod. Phys., 75:543, 2003.
[108] D. SUGNy, A. KELLER, O. ATABEK, D. DAEMS, C. DioN, S.
GUERiN et H. R. JAUSLiN : Reaching optimally oriented molecular states by laser
kicks. Phys. Rev. A, 69:033402, 2004.
[109] H. J. SUSSMANN et G. TANG : Shortest paths for the
Reeds-Shepp car : a worked out example of the use of geometric techniques in
nonlinear optimal control. Rutgers Center for Systems and Control Technical
Report 91-10, 1991.
[110] Héctor J. SUSSMANN : Shortest 3-dimensional paths
with a prescribed curvature bound. In Proceedings of the 34th IEEE
Conference on Decision and Control, 1995.
[111] G. TAyLoR : Analysis of the swimming of microscopic
organisms. Proc. Roy. Soc. London. Ser. A., 209:447-461, 1951.
[112] Stefan TEUFEL : Adiabatic perturbation theory in
quantum dynamics, volume 1821 de Lecture Notes in Mathematics.
Springer-Verlag, Berlin, 2003.
[113] Mikhail TEyTEL : How rare are multiple eigenvalues?
Comm. Pure Appl. Math., 52(8): 917-934, 1999.
[114] Gabriel TURiNici : On the controllability of bilinear
quantum systems. In M. DEFRANcEScHi et C. LE BRiS, éditeurs
: Mathematical models and methods for ab initio Quantum Chemistry,
volume 74 de Lecture Notes in Chemistry. Springer, 2000.
[115] Karen UHLENBEcK : Eigenfunctions of Laplace operators.
Bull. Amer. Math. Soc., 78: 1073-1076, 1972.
[116] Enrique ZUAzUA : Switching controls. Journal of the
European Mathematical Society, à paraître.
| 


