I.2 THEORIE METRIQUE DE LA GRAVITATION
La théorie de NEWTON de la gravitation
présente des difficultés conceptuelles comme celle de l'action
à distance. Ce qui veut qu'une variation du champ gravitationnel est
transmise instantanément dans tout l'espace -- temps
galiléen11.
Depuis 1905, l'espace -- temps galiléen est
rejeté à la lumière de la relativité restreinte car
l'équation fondamentale de la dynamique et la loi d'attraction
gravitationnelle sont invariantes sous une transformation de
GALILEE. Il faut donc une théorie relativiste de la
gravitation.
10 Voir lexique
11 Voir lexique
dans l'approximation linéaire du champ
Ladite théorie relativiste de la gravitation est
construite dans l'espace - temps de MINKOWSKI12 ;
On définit par , ì = les coordonnées minkowskiennes d'un
événement M (c'est aussi sa ligne
d'univers).
La théorie relativiste de la dynamique est formulée
pour un observateur inertiel. Soit un champ de
Quadri - forces extérieures , celles - ci dérivent
d'un potentiel Ö . Alors la loi relativiste
de la dynamique s'écrit
F ? ( x ? ( s
(I.7)
où est la quadri - vitesse, s
est le temps propre et la ligne d'univers de la particule La
quadri - accélération est orthogonale à
:
(I.8) Pour assurer la compatibilité, on admet la
condition algébrique suivante :
(I.9)
La quadri - quantité de mouvement : F
(I.10)
|
Comme
|
dérive du potentiel Ö (car ) on sait par ailleurs
que
|
|
|

|
; le théorème de Gauss pour le champ de
composantes est :
|
12 Voir lexique
dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp
Il en ressort l'équation de poisson :
(I.12) Où G est la constante
de NEWTON, est la masse grave volumique.
II. 2.1 Espace - temps
einsteinien13
La géométrie de l'espace-temps minkowskien est tout
à fait satisfaisante pour décrire la réalité
physique tant que les effets gravitationnels ne sont pas pris en compte. Le
fait qu'il
faille nécessairement décrire globalement les
phénomènes physiques dans l'univers implique que nous devons
considérer les effets de la gravitation sur ceux-ci .Pour cela nous
admettons que ces effets résultent uniquement de la structure
géométrique l'espace-temps minkowskien, pour adopter
l'espace-temps Einsteinien dont la géométrie est Lorentzienne
caractérisée par une métrique14
g de signature15 et de la connexion
riemannienne16 associe à la métrique
g. L'espace-temps einsteinien décrit un
véritable champ de gravitation si le tenseur de
RIEMANN17 est non nul, donc si l'espace-temps est
courbe et non localement plat .Le principe de covariance stipule qu'il n'existe
pas de systèmes privilégiés de coordonnées, alors
les champs physiques sont des champs de tenseurs et les lois physiques
s'écrivent de façon tensorielle dans n'importe quel
système de coordonnées, éventuellement limites à
ceux de la matrice Jacobienne de déterminant positif nécessitant
que l'espace-temps soit orientable. Donc pour un champ tenseur
T on a :
(I.14)
13 Voir lexique
14 Voir lexique
15 Voir lexique
16 Voir lexique
17 Voir lexique
dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp
I.2.2 Formalisme Lagrangien dans le cas d'un champ
classique
Dans l'espace-temps minkowskien, les champs classiques (scalaire,
électromagnétique,...) ont des équations de champ quoi
dérivent d'un Lagrangien. En notant contenant de
façon générique et ses
dérivées , on sait que est un scalaire. Dans l'espace -- temps
einsteinien, d'après le principe d'équivalence
d'EINSTEIN, on remplace par et alYIM
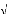
par dans l'expression du Lagrangien noté qui reste donc un
scalaire. L'action
associée au Lagrangien L est
l'intégrale de la densité lagrangienne L = dans
un domaine
Ù de l'espace -- temps Einsteinien :
(I.15) 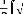
sM ??est indépendante du
choix du système de coordonnées .La variation de
sm par rapport à
??
donne les équations de champs :
(I.16) La variation de l'action de par rapport à ou par
rapport à définit le tenseur
énergie -- impulsion
symétrique :
(I.17)
|
(I.18)
|
(I.19)
|
(I.20)
|
(I.21)
|
(I.22)
|
(I.23)
|
(I.17)
|
|
|
|
|
|
|
|
|
n'est possible qu'à l'approximation quasi-classique
où
|
|
dans la limite .
|
suivant que l'on fait apparaître ou dans la densité
Lagrangienne en faisant attention au
signe puisque . On peut donc voir ici que
l'espace -- temps Einsteinien
étantdonné, les champs classiques peuvent titres
quantifiés, comme nous le verrons dans la suite de
notre travail.
Dans le cas d'un champ scalaire, la description quantique d'une
seule particule par une onde
dans l'approximation linéaire du champ
La phase de l'onde est gouvernée par une
équation18 que nous verrons dans la suite.
I.3. ELEMENTS DE LA THEORIE D'EINSTEIN DE LA GRAVITATION
OU RELATIVITE GENERALE
I.3.1 Equations d'EINSTEIN de la gravitation
On admet que l'espace -- temps est une variété
différentiable munie d'une métrique Lorentzienne g, la
gravitation étant une manifestation de la structure
géométrique de l'espace -- temps.
Les idées suivantes conduisent aux équations
d'EINSTEIN de la gravitation :
a) les équations de la gravitation devront être
tensorielles. On peut les écrire dans n'importe quel système de
coordonnées ; c'est le principe de covariance déjà
invoqué. Pour déterminer les composantes de la métrique,
il faut une source de même
nature tensorielle .Le tenseur énergie - impulsion
qui contient la densité de masse ñ
semble tout indiqué (également respectivement
le principe de covariance
).
b) ,Il est rEOonnIIle MLgIr qN lAffpquaVINQ
VIR Mamp gravMIonnel soiHJ des équations aux dérivées
partielles du second ordre de façon à généraliser
les équations de POISSON de la théorie
de NEWTON de la gravitation ( ).
On doit donc trouver un tenseur géométrique deux
fois covariant dépendant
uniquement de et de ses dérivées jusqu'au second
ordre qui satisfasse .
On a :
(I.18)
et qui sont les deux tenseurs possibles.
18 Voir lexique
dans l'approximation linéaire du champ
Les équations d'EINSTEIN de la
gravitation sont :
(I.19)
c
où ÷ est la constante couplage gravitationnel de
dimension ; Ë est la constante
cosmologique de dimension .
Ces équations non linéaires relient la
géométrie de l'espace - temps et la distribution
énergétique de la matière,
déterminent les composantes de la métrique dans un certain
système de coordonnées ( ). Elles
nécessitent des conditions aux limites : en dehors de la
matière , les solutions sont celles du vide ;
pour
la métrique Minkowskienne alors l'espace - temps
Minkowskien est une solution
particuliJqre du vide lorsque Ë = 0 .
Donc hors du champ cosmologique
p
(I.20)
La valeur de ÷ est fixée :
(I.21) On constate généralement que la
théorie d'EINSTEIN de la gravitation n'est plus valable
à
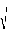
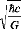
des distances de l'ordre de , pour des masses de l'ordre de
, pour des temps
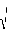
de l'ordre , pour des énergies d'interaction de l'ordre
de
(Qui sont tous respectivement la distance, masse, temps,
énergie de PLANCK)19 puisqu'il faudrait une
théorie quantique de la gravitation pour décrire ces domaines. Ce
qui fera l'objet du paragraphe sur la théorie de BOHM
de la gravitation.
19 Voir constantes et abréviations
dans l'approximation linéaire du champ g ? ?
? h avec
| 


