La théorie de la gravité quantique de Bohm dans l'approximation linéaire du champ

II.1 CAS DE L'APPROXIMATION NEWTONIENNE

Dans le cas où l'on applique ces résultats à l'approximation newtonienne, on aura la métrique donnée par :

(II.15)

Où est le potentiel gravitationnel de NEWTON. Le champ est donné par

; ; (II.16)

et nous avons les identités :

. (II.17)

On a :

(II.18)

Cette dernière équation est l'équation d' HAMILTON - JACOBI modifiée sous forme simplifiée³³. Et on a l'équation de continuité qui simplifiée de la meme façon que l'équation précédente comme suit :

(II.19)

Ainsi le potentiel quantique s'écrira donc :

(II.20)

Pour ce qui est des équations des trajectoires de BOHM on obtient :

³³ Ici on fait partir les indices des tenseurs, on reste avec les simples grandeurs scalaires usuelles.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

(II.21)

Dans l'approximation newtonienne, le potentiel gravitationnel est constant dans le temps donc 0 # f(t) ao = 0 , ceci à cause de la j auge harmonique : aPo_i,= 0 pour la relation (II.21),cela implique que :

(II.22)

C'est le cas où le potentiel quantique est du même ordre de grandeur que le potentiel classique, ainsi ce potentiel³⁴ est non négligeable.

(II.22) dans (II.18) . On se souvient que l'on a pris

en (I.32) or on sait qu'en mécanique quantique la fonction d'onde non

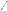
stationnaire s'écrit , en se référant à cela on peut poser : ceci parce

1 que dans le domaine Newtonien, les grandeurs physiques ne doivent pas dépendre du temps
(puisqu'ici on considère des cas stationnaires pour l'approximation Newtonienne). Pour ce la
l'équation de continuité (II.19) est donc identiquement satisfaite si on considère (II.22) et le fait

que De même comme en (II.14) on peut obtenir l'équation du champ :

(II.18) au regard de (II.22) devient : or

Nous obtenons l'équation de champ, de l'approximation Newtonienne provenant de la théorie de BOHM :

(II.23)

Ici nous avons juste considéré le champ linéaire de la gravité quantique de BOHM, en ignorant celui créé par source de matière. D'après l'idée de BOHM de la gravitation quantique on

³⁴ Il s'agit du potentiel quantique.

dans l'approximation linéaire du champ

doit donc introduire ce terme³⁵, l'équation de POISSON s'écrira dans l'approximation Newtonienne de la manière suivante :

(II.24)

Dans ce cadre de l'approximation Newtonienne de la gravité quantique de BOHM, déterminons l'expression du potentiel quantique ; Pour cela choisissons R la norme du paquet d'onde autour de la solution classique de l'équation du champ gravitationnel :

(II.25)

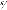
où et sont respectivement un paramètre d'extinction et le champ quantique ; On a la

fonction d'onde ; Le terme R est équivalent à celui de la fonction

d'onde d'un oscillateur harmonique quantique, sauf qu'ici la variable est le champ gravitationnel, ? ?
au lieu de la position comme dans le cas de l'oscillateur.

D'après BOHM le champ total est 0 donné par :

(II.26)

où est le potentiel gravitationnel classique solution de l'équation de POISSON, on a
en remplaçant dans l'expression de R on a :

(II.27)

Bien sûr la constante « » rassure sur le fait que l'on n'ait pas une fonction d'onde dont
la norme tend vers l'infini à mesure que le champ tend vers l'infini.

³⁵ On doit ajouter le terme classique de la source de matière .

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Si on omet Q dans l'équation (II.24), satisfera celle -- ci. Si on remplace cette expression

de R dans celle de Q :

(II.28)

Ici on considère que . On sait que l'équation de champ dans la théorie de BOHM est :

(II.29)

Prenons le cas où on a comme source de matière, un point matériel alors on peut écrire

(II.30)

Alors pour résoudre (II.29) on se sert de (II.26). On doit avoir :

(II.31)

Où M, r sont respectivement la masse de la source de matière et la distance entre elle et le point où le champ dérivant de Oc est créé. L'équation (II.29) s'écrit :

		(II.32)
En explicitant le Laplacien on aura :

En coordonnées sphériques³⁶ :

(II.33)

³⁶ Dans un système de coordonnées sphériques correspondant à une base orthonormée.

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

Pour résoudre (II.33) utilisons la méthode de séparation des variables et on obtient le système suivant :

(II.34)

En considérant une source de matière à symétrie sphérique et statique seule la première équation de (II.34) nous intéresse :

				(II.35)

Cette équation (II.35) est une équation de la forme de celles de BESSEL de première espèce³⁷. Ici

d²U dU

on aura , a= 2 et b = ot² . La solution sera donc :

(II.36)

La solution est donc :

(II.37)

OA Ces constantes ont la même unité que le champ gravitationnel
classique. La solution sera alors :

(II.38)

Certains points de cette solution sont intéressants :

³⁷ Qui est de la forme :

dEns Bl'EpprRxiPEtiRn BlinéEire Bdu BAhEPp

ü Par exemple aux grandes distances r de la source de matière, le comportement asymptotique des fonctions sphériques de BESSEL :

(II.39)

On constate bien que la solution quantique est inversement proportionnelle à r aux grandes distances de la source.

ü Si la masse de la source de matière est négligeable ( --> 0 ), on a , ainsi on a une

pure solution quantique dans laquelle on a une petite source de gravité .Cela signifie que les fluctuations quantiques de la gravité peuvent produire une gravité observable.

Il doit etre noté que l'approximation du champ faible est seulement applicable aux grandes distances .Ainsi cette solution ne donne aucune information concernant les cas des singularités et horizons gravitationnels.

ü A cause de la nature oscillatoire des fonctions sphériques de BESSEL, le potentiel gravitationnel est aussi oscillatoire .Ainsi nous avons un ensemble de points stables et périodiques, où le potentiel est minimum et une particule -- test peut etre au repos à d'autres positions³⁸. Il doit etre noté que, si nous choisissons un fin paquet d'ondes³⁹, la fréquence des oscillations est très grande.